6.3: Factorización de números naturales primos

Última actualización
Guardar como PDF

Page ID: 161778

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

ser capaz de determinar los factores de un número entero
ser capaz de distinguir entre números primos y compuestos
estar familiarizado con el principio fundamental de la aritmética
poder encontrar la factorización prima de un número entero

Factores

De las observaciones realizadas en el proceso de multiplicación, hemos visto que

$(\text{factor}) \cdot (\text{factor}) = \text{product}$

Factores, Producto
Los dos números que se multiplican son los factores y el resultado de la multiplicación es el producto. Ahora, usando nuestro conocimiento de división, podemos ver que un primer número es un factor de un segundo número si el primer número se divide en el segundo número un número entero de veces (sin un resto).

Un número como factor de otro
Un primer número es un factor de un segundo número si el primer número se divide en el segundo número un número entero de veces (sin un resto).

Esto lo mostramos en los siguientes ejemplos:

Ejemplo$\PageIndex{1}$

3 es un factor de 27, ya que$27 \div 3 = 9$, o$3 \cdot 9 = 27$.

Ejemplo$\PageIndex{2}$

7 es un factor de 56, ya que$56 \div 7 = 8$, o$7 \cdot 8 = 56$.

Ejemplo$\PageIndex{3}$

4 no es un factor de 10, ya que$10 \div 4 = \text{2R2}$. (Hay un resto.)

Determinar los factores de un número entero

Podemos utilizar las pruebas de divisibilidad de [link] para determinar todos los factores de un número entero.

Conjunto de Muestras A

Encuentra todos los factores de 24.

Solución

$\begin{array} {lll} {\text{Try 1:}} & {24 \div 1 = 24} & {\text{1 and 24 are factors}} \\ {\text{Try 2:}} & {\text{24 is even, so 24 is divisible by 2.}} & {} \\ {} & {24 \div 2 = 12} & {\text{2 and 12 are factors}} \\ {\text{Try 3:}} & {2 + 4 = 6 \text{ and 6 is divisible by 3, so 24 is divisible by 3.}} & {} \\ {} & {24 \div 3 = 8} & {\text{3 and 8 are factors}} \\ {\text{Try 4:}} & {24 \div 4 = 6} & {\text{4 and 6 are factors}} \\ {\text{Try 5:}} & {24 \div 5 = \text{4R4}} & {\text{5 is not a factor}} \end{array}$

El siguiente número a probar es 6, pero ya tenemos que 6 es un factor. Una vez que nos encontramos con un factor que ya hemos descubierto, podemos detenernos.

Todos los factores numéricos enteros de 24 son 1, 2, 3, 4, 6, 8, 12 y 24.

Conjunto de práctica A

Encuentra todos los factores de cada uno de los siguientes números.

Responder: 1, 2, 3, 6

Conjunto de práctica A

Responder: 1, 2, 3, 4, 6, 12

Conjunto de práctica A

Responder: 1, 2, 3, 6, 9, 18

Conjunto de práctica A

Responder: 1, 5

Conjunto de práctica A

Responder: 1, 2, 5, 10

Conjunto de práctica A

Responder: 1, 3, 11, 33

Conjunto de práctica A

Responder: 1, 19

Números primos y compuestos

Observe que los únicos factores de 7 son 1 y 7 en sí, y que los únicos factores de 3 son 1 y 3 en sí. Sin embargo, el número 8 tiene los factores 1, 2, 4 y 8, y el número 10 tiene los factores 1, 2, 5 y 10. Así, podemos ver que un número entero puede tener sólo dos factores (él mismo y 1) y otro número entero puede tener varios factores.

Podemos usar esta observación para hacer una clasificación útil para números enteros: números primos y números compuestos.

Definición: Prime Number

Un número entero (mayor que uno) cuyos únicos factores son él mismo y 1 se llama número primo.

El Número 1 no es un número primo
Los primeros siete números primos son 2, 3, 5, 7, 11, 13 y 17. Observe que el número entero 1 no se considera un número primo, y el número entero 2 es el primer número primo y el único número primo par.

Definición: Número compuesto

Un número entero compuesto por factores distintos a sí mismo y 1 se llama número compuesto. Los números compuestos no son números primos.

Algunos números compuestos son 4, 6, 8, 9, 10, 12 y 15.

Conjunto de Muestras B

Determine qué números enteros son primos y cuáles son compuestos.

39. Dado que 3 se divide en 39, el número 39 es compuesto:$39 \div 3 = 13$

Conjunto de Muestras B

47. Unos cuantos juicios de división nos asegurarán que 47 sólo es divisible por 1 y 47. Por lo tanto, 47 es primo.

Set de práctica B

Determine cuáles de los siguientes números enteros son primos y cuáles son compuestos.

Responder: prime

Set de práctica B

Responder: compuesto

Set de práctica B

Responder: compuesto

Set de práctica B

Responder: compuesto

Set de práctica B

Responder: prime

Set de práctica B

Responder: prime

Set de práctica B

101

Responder: prime

Set de práctica B

Responder: compuesto

El principio fundamental de la aritmética

Los números primos son muy útiles en el estudio de las matemáticas. Veremos cómo se utilizan en secciones posteriores. Ahora declaramos el Principio Fundamental de la Aritmética.

Principio Fundamental de Aritmética
Excepto por el orden de los factores, cada número natural que no sea 1 puede ser factorizado de una y sólo una manera como producto de números primos.

Definición: Factorización Prime

Cuando se descompone un número de modo que todos sus factores son números primos. La factorización se llama la factorización primo del número.

La técnica de factorización prima se ilustra en los siguientes tres ejemplos.

$10 = 5 \cdot 2$. Tanto 2 como 5 son primos. Por lo tanto,$2 \cdot 5$ es la factorización prima de 10.
11. El número 11 es un número primo. La factorización de primos se aplica solo a los números compuestos. Así, 11 no tiene descomposición primo.
$60 = 2 \cdot 30$. El número 30 no es primo:$30 = 2 \cdot 15$.

$60 = 2 \cdot 2 \cdot 15$

El número 15 no es primo:$15 = 3 \times 5$

$60 = 2 \cdot 2 \cdot 3 \cdot 5$

Utilizaremos exponentes.

$60 = 2^2 \cdot 3 \cdot 5$

Los números 2, 3 y 5 son primos cada uno. Por lo tanto,$2^2 \cdot 3 \cdot 5$ es la factorización prima de 60.

La factorización principal de un número natural

El siguiente método proporciona una manera de encontrar la factorización prima de un número natural.

El método para encontrar la factorización prima de un número natural

Divide el número repetidamente por el número primo más pequeño que dividirá en él un número entero de veces (sin un resto).
Cuando el número primo utilizado en el paso 1 ya no se divida en el número dado sin un resto, repita el proceso de división con el siguiente primo más grande que divide el número dado.
Continuar con este proceso hasta que el cociente sea menor que el divisor.
La descomposición como primo del número dado es el producto de todos estos divisores primos. Si el número no tiene divisores primos, es un número primo.

Es posible que podamos usar algunas de las pruebas de divisibilidad que estudiamos en [link] para ayudar a encontrar los primos que dividen el número dado.

Conjunto de Muestras C

Encuentra la factorización prime de 60.

Solución

Dado que el último dígito de 60 es 0, que es par, 60 es divisible por 2. Vamos a dividir repetidamente por 2 hasta que ya no podamos. Dividiremos de la siguiente manera:

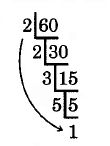
$\begin{array} {l} {\text{30 is divisible by 2 again}} \\ {\text{15 is not divisible by 2, but it is divisible by 3, the next prime}} \\ {\text{5 is not divisible by 3, but it is divisible by 5, the next prime.}} \end{array}$

El cociente 1 es finalmente más pequeño que el divisor 5, y la descomposición como primo de 60 es el producto de estos divisores primos.

$60 = 2 \cdot 2 \cdot 3 \cdot 5$

Utilizamos exponentes cuando es posible.

$60 = 2^2 \cdot 3 \cdot 5$

Conjunto de Muestras C

Encuentra la factorización prima de 441.

Solución

441 no es divisible por 2 ya que su último dígito no es divisible por 2.

441 es divisible por 3 desde$4 + 4 + 1 = 9$ y 9 es divisible por 3.

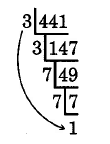
$441 dividido por 3 es 147. 147 dividido por 3 es 49. 49 dividido por 7 es 7. 7 dividido por 7 es 1.$

$\begin{array} {l} {\text{147 is divisible by } 3(1 + 4 + 7 = 12).} \\ {\text{49 is not divisible by 3, nor is it divisible by 5. It is divisible by 7.}} \end{array}$

El cociente 1 es finalmente más pequeño que el divisor 7, y la descomposición como primo de 441 es el producto de estos divisores primos.

$441 = 3 \cdot 3 \cdot 7 \cdot 7$

Usa exponentes.

$441 = 3^2 \cdot 7^2$

Conjunto de Muestras C

Encuentra la factorización prima de 31.

Solución

$\begin{array} {ll} {\text{31 is not divisible by 2}} & {\text{Its last digit is not even}} \\ {} & {31 \div 2 = \text{15R1}} \\ {} & {\text{The quotient, 15, is larger than the divisor, 3. Continue.}} \\ {\text{31 is not divisible by 3}} & {\text{The digits } 3 + 1 = 4, \text{ and 4 is not divisible by 3.}} \\ {} & {31 \div 3 = \text{10R1}} \\ {} & {\text{The quotient, 10, is larger than the divisor, 3. Continue.}} \\ {\text{31 is not divisible by 5}} & {\text{The last digit of 31 is not 0 or 5.}} \\ {} & {31 \div 5 = \text{6R1}} \\ {} & {\text{The quotient, 6, is larger than the divisor, 5. Continue.}} \\ {\text{31 is not divisible by 7.}} & {\text{Divide by 7.}} \\ {} & {31 \div 7 = \text{4R1}} \\ {} & {\text{The quotient, 4 is smaller than the divisor, 7.}} \\ {} & {\text{We can stop the process and conclude that 31 is a prime number.}} \end{array}$

El número 31 es un número primo

Set de práctica C

Encuentra la factorización primo de cada número entero.

Responder: $22 = 2 \cdot 11$

Set de práctica C

Responder: $40 = 2^3 \cdot 5$

Set de práctica C

Responder: $48 = 2^4 \cdot 3$

Set de práctica C

Responder: $63 = 3^2 \cdot 7$

Set de práctica C

945

Responder: $945 = 3^3 \cdot 5 \cdot 7$

Set de práctica C

1,617

Responder: $1617 = 3 \cdot 7^2 \cdot 11$

Set de práctica C

Responder: 17 es primo

Set de práctica C

Responder: 61 es primo

Ejercicios

Para los siguientes problemas, determine el/los factor (es) faltante (es).

Ejercicio$\PageIndex{1}$

$14 = 7 \cdot $

Responder: 2

Ejercicio$\PageIndex{2}$

$20 = 4 \cdot $

Ejercicio$\PageIndex{3}$

$36 = 9 \cdot $

Responder: 4

Ejercicio$\PageIndex{4}$

$42 = 21 \cdot $

Ejercicio$\PageIndex{5}$

$44 = 4 \cdot $

Responder: 11

Ejercicio$\PageIndex{6}$

$38 = 2 \cdot $

Ejercicio$\PageIndex{7}$

$18 = 3 \cdot $.

Responder: $3 \cdot 2$

Ejercicio$\PageIndex{8}$

$28 = 2 \cdot $.

Ejercicio$\PageIndex{9}$

$300 = 2 \cdot 5 \cdot $.

Responder: $2 \cdot 3 \cdot 5$

Ejercicio$\PageIndex{10}$

$840 = 2 \cdot $.

Para los siguientes problemas, encuentra todos los factores de cada uno de los números.

Ejercicio$\PageIndex{11}$

Responder: 1, 2, 4, 8, 16

Ejercicio$\PageIndex{12}$

Ejercicio$\PageIndex{13}$

Responder: 1, 2, 4, 7, 8, 14, 28, 56

Ejercicio$\PageIndex{14}$

105

Ejercicio$\PageIndex{15}$

220

Responder: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220

Ejercicio$\PageIndex{16}$

Ejercicio$\PageIndex{17}$

Responder: 1, 2, 4, 8, 16, 32

Ejercicio$\PageIndex{18}$

Ejercicio$\PageIndex{19}$

142

Responder: 1, 2, 71, 142

Ejercicio$\PageIndex{20}$

218

Para los siguientes problemas, determine cuáles de los números enteros son primos y cuáles son compuestos.

Ejercicio$\PageIndex{21}$

Responder: prime

Ejercicio$\PageIndex{22}$

Ejercicio$\PageIndex{23}$

Responder: compuesto

Ejercicio$\PageIndex{24}$

Ejercicio$\PageIndex{25}$

Responder: prime

Ejercicio$\PageIndex{26}$

Ejercicio$\PageIndex{27}$

Responder: prime

Ejercicio$\PageIndex{28}$

Ejercicio$\PageIndex{29}$

Responder: prime

Ejercicio$\PageIndex{30}$

Ejercicio$\PageIndex{31}$

Responder: compuesto ($5 \cdot 11$)

Ejercicio$\PageIndex{32}$

Ejercicio$\PageIndex{33}$

1,044

Responder: compuesto

Ejercicio$\PageIndex{34}$

924

Ejercicio$\PageIndex{35}$

339

Responder: compuesto

Ejercicio$\PageIndex{36}$

103

Ejercicio$\PageIndex{37}$

209

Responder: compuesto$(11 \cdot 19)$

Ejercicio$\PageIndex{38}$

667

Ejercicio$\PageIndex{39}$

4,575

Responder: compuesto

Ejercicio$\PageIndex{40}$

119

Para los siguientes problemas, encuentra la factorización prima de cada uno de los números enteros.

Ejercicio$\PageIndex{41}$

Responder: $2 \cdot 13$

Ejercicio$\PageIndex{42}$

Ejercicio$\PageIndex{43}$

Responder: $2 \cdot 3^3$

Ejercicio$\PageIndex{44}$

Ejercicio$\PageIndex{45}$

Responder: $2^3 \cdot 7$

Ejercicio$\PageIndex{46}$

176

Ejercicio$\PageIndex{47}$

480

Responder: $2^5 \cdot 3 \cdot 5$

Ejercicio$\PageIndex{48}$

819

Ejercicio$\PageIndex{49}$

2,025

Contestar: $3^4 \cdot 5^2$

Ejercicio$\PageIndex{50}$

148,225

Ejercicios para revisión

Ejercicio$\PageIndex{51}$

Redondear 26,584 al diez más cercano.

Contestar: 26,580

Ejercicio$\PageIndex{52}$

¿Cuánto más grande es 106 que 79?

Ejercicio$\PageIndex{53}$

¿Verdadero o falso? El cero dividido por cualquier número entero distinto de cero es cero.

Contestar: true

Ejercicio$\PageIndex{54}$

Encuentra el cociente. $10,584 \div 126.$

Ejercicio$\PageIndex{55}$

Encuentra el valor de$\sqrt{121} - \sqrt{81} + 6^2 \div 3$.

Contestar: 14

Search

Text Color

Text Size

Margin Size

Font Type