Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.1: Lectura y escritura de decimales

Última actualización

10 may 2023
Guardar como PDF
- 9: Decimales
- 9.2: Convertir un decimal a una fracción

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

entender el significado de los dígitos que ocurren a la derecha de la posición de unos
estar familiarizado con el significado de las fracciones decimales
ser capaz de leer y escribir una fracción decimal

Dígitos a la derecha de la posición de unos

Comenzamos nuestro estudio de la aritmética señalando que nuestro sistema numérico se llama sistema de números posicionales con base diez. También señalamos que cada posición tiene un valor particular. Observamos que cada posición tiene diez veces el valor de la posición a su derecha.

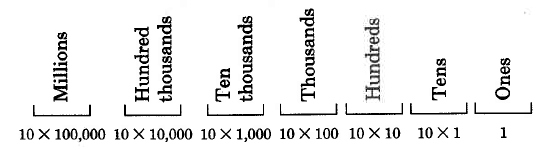
$10 veces 100,000 es la posición de millones. 10 veces 10,000 es la posición de cien miles. 10 veces 1,000 es la posición de diez miles. 10 veces 100 es la posición de miles. 10 veces 10 es la posición de cientos. 10 veces 1 es la posición de decenas. 1 es la posición de unos.$

Esto significa que cada posición tiene $\dfrac{1}{10}$ el valor de la posición a su izquierda.

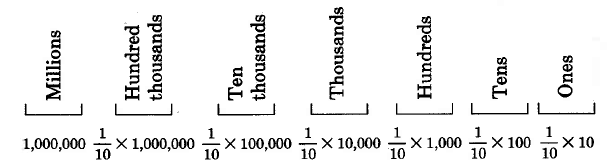
$1,000,000 es la posición de millones. Una décima parte de 1,000,000 son los cien miles. Una décimas de 100 mil son los diez miles. Una décima parte de 10 mil es la posición de miles. Una décima parte de mil son los miles. Una décima parte de 100 es la posición de las decenas. Una décima parte de 10 es la posición de unos.$

Así, un dígito escrito a la derecha de la posición de las unidades debe tener un valor $\dfrac{1}{10}$ de 1. Recordando que la palabra “de” se traduce en multiplicación $(\cdot)$ , podemos ver que el valor de la primera posición a la derecha del dígito de unidades es $\dfrac{1}{10}$ de 1, o

$\dfrac{1}{10} \cdot 1 = \dfrac{1}{10}$

El valor de la segunda posición a la derecha del dígito de las unidades es $\dfrac{1}{10}$ de $\dfrac{1}{10}$ , o

$\dfrac{1}{10} \cdot \dfrac{1}{10} = \dfrac{1}{10^2} = \dfrac{1}{100}$

El valor de la tercera posición a la derecha del dígito de las unidades es $\dfrac{1}{10}$ de $\dfrac{1}{100}$ , o

$\dfrac{1}{10} \cdot \dfrac{1}{100} = \dfrac{1}{10^3} = \dfrac{1}{1000}$

Este patrón continúa.

Ahora podemos ver que si tuviéramos que escribir dígitos en posiciones a la derecha de las posiciones de las unidades, esas posiciones tienen valores que son fracciones. No sólo las posiciones tienen valores fraccionarios, sino que los valores fraccionarios son todos potencias de 10 $(10, 10^2, 10^3, ...)$ .

Fracciones decimales

Punto decimal, Decimal
Si vamos a escribir números con dígitos que aparecen a la derecha del dígito de unidades, debemos tener una forma de denotar donde termina la parte del número entero y comienza la parte fraccionaria. Los matemáticos denotan el punto de separación del dígito de unidades y el dígito décimas escribiendo un punto decimal. La palabra decimal proviene del prefijo latino “deci” que significa diez, y la usamos porque usamos un sistema de números base diez. Los números escritos en esta forma se denominan fracciones decimales, o más simplemente, decimales.

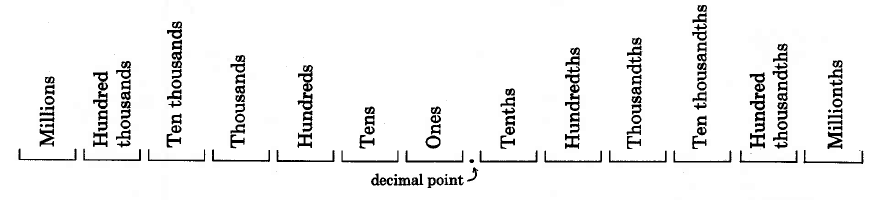
$millones, cien miles, diez miles, miles, cientos, decenas y unos están a la izquierda del punto decimales. décimas, centésimas, milésimas, diez milésimas, cien milésimas y millonésimas están a la derecha del punto decimal.$

Observe que los números decimales tienen el sufijo “th”.

Fracción decimal
Una fracción decimal es una fracción en la que el denominador es una potencia de 10.

Los siguientes números son ejemplos de decimales.

42.6

El 6 está en la posición décimas.

$42.6 = 42 \dfrac{6}{10}$
9.8014

El 8 está en la posición décimas.
El 0 está en la posición de centésimas.
El 1 está en la posición milésimas.
El 4 está en la posición de las diez milésimas.

$9.8014 = 9 \dfrac{8014}{10,000}$
0.93

El 9 está en la posición décimas.
El 3 está en la posición de centésimas.

$0.93 = \dfrac{93}{100}$

Nota

Muy a menudo se inserta un cero delante de un punto decimal (en la posición de unidades) de una fracción decimal que tiene un valor menor que uno. Este cero nos ayuda a evitar pasar por alto el punto decimal.

0.7

El 7 está en la posición décimas.

$0.7 = \dfrac{7}{10}$

Nota

Podemos insertar ceros a la derecha del dígito más a la derecha en una fracción decimal sin cambiar el valor del número.

$\dfrac{7}{10} = 0.7 = 0.70 = \dfrac{70}{100} = \dfrac{7}{10}$

Lectura de fracciones decimales

Lectura de una fracción decimal
Para leer una fracción decimal,

Lee toda la parte del número como de costumbre. (Si el número entero es menor que 1, omita los pasos 1 y 2).
Lee el punto decimal como la palabra “y”.
Lee el número a la derecha del punto decimal como si se tratara de un número entero.
Di el nombre de la posición del último dígito.

Conjunto de Muestras A

Lee los siguientes números.

6.8

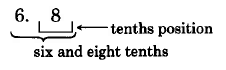
$6.8 son seis y ocho décimas. El 8 está en la posición décimas.$

Nota

Algunas personas leen esto como “seis punto ocho”. Este fraseo transmite el mensaje, pero técnicamente, “seis y ocho décimas” es el fraseo correcto.

Conjunto de Muestras A

14.116

$14.116 es catorce y ciento dieciséis milésimas. El seis está en la posición milésimas.$

Conjunto de Muestras A

0.0019

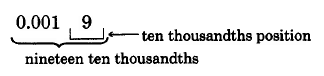
$0.0019 es diecinueve diez milésimas. El nueve se encuentra en la posición de las diez milésimas.$

Conjunto de Muestras A

Ochenta y uno

En este problema, la indicación es que cualquier número entero es una fracción decimal. Los números enteros a menudo se llaman números decimales.

$81 = 81.0$

Conjunto de práctica A

Lee las siguientes fracciones decimales.

12.9

Responder: doce y nueve décimas

Conjunto de práctica A

4.86

Responder: cuatro y ochenta y seis centésimas

Conjunto de práctica A

7.00002

Responder: setecientos milésimas

Conjunto de práctica A

0.030405

Responder: treinta mil cuatrocientos cinco millonésimas

Escribir fracciones decimales

Escribir una Fracción Decimal
Para escribir una fracción decimal,

Escribe toda la parte del número.
Escriba un punto decimal para la palabra “y”.
Escribe la parte decimal del número para que el dígito más a la derecha aparezca en la posición indicada en el nombre de la palabra. Si es necesario, inserte ceros a la derecha del punto decimal para que el dígito más a la derecha aparezca en la posición correcta.

Conjunto de Muestras B

Escribe cada número.

Treinta y uno y doce centésimas.

Solución

La posición decimal indicada es la posición de centésimas.

31.12

Conjunto de Muestras B

Dos y trescientas milésimas.

Solución

La posición decimal indicada es la de las cien milésimas. Tendremos que insertar suficientes ceros a la derecha inmediata del punto decimal para ubicar el 3 en la posición correcta.

2.00003

Conjunto de Muestras B

Seis mil veintisiete ciento cuatro millonésimas.

Solución

La posición decimal indicada es la posición millonésima. Tendremos que insertar suficientes ceros a la derecha inmediata del punto decimal para ubicar el 4 en la posición correcta.

6,027.000104

Conjunto de Muestras B

Diecisiete centésimas.

Solución

La posición decimal indicada es la posición de centésimas.

0.17

Set de práctica B

Escribe cada fracción decimal.

Trescientos seis y cuarenta y nueve centésimas.

Responder: 306.49

Set de práctica B

Nueve y cuatro milésimas.

Responder: 9.004

Set de práctica B

Sesenta y un millonésimas.

Responder: 0.000061

Ejercicios

Para los tres problemas siguientes, dar el nombre decimal de la posición del número dado en cada fracción decimal.

Ejercicio $\PageIndex{1}$

1. 3.941
9 está en la posición.
4 está en la posición.
1 está en la posición.

Responder: Décimas; centésimas, milésimas

Ejercicio $\PageIndex{2}$

17.1085
1 está en la posición.
0 está en la posición.
8 está en la posición.
5 está en la posición.

Ejercicio $\PageIndex{3}$

652.3561927
9 está en la posición.
7 está en la posición.

Responder: Cien milésimas; diez millonésimas

Para los siguientes 7 problemas, lea cada fracción decimal escribiéndola.

Ejercicio $\PageIndex{4}$

9.2

Ejercicio $\PageIndex{5}$

8.1

Responder: ocho y una décima

Ejercicio $\PageIndex{6}$

10.15

Ejercicio $\PageIndex{7}$

55.06

Responder: cincuenta y cinco y seis centésimas

Ejercicio $\PageIndex{8}$

0.78

Ejercicio $\PageIndex{9}$

1.904

Responder: mil novecientos cuatro milésimas

Ejercicio $\PageIndex{10}$

10.00011

Para los siguientes 10 problemas, escriba cada fracción decimal.

Ejercicio $\PageIndex{11}$

Tres y veinte centésimas.

Responder: 3.20

Ejercicio $\PageIndex{12}$

Catorce y sesenta y siete centésimas.

Ejercicio $\PageIndex{13}$

Una y ocho décimas.

Responder: 1.8

Ejercicio $\PageIndex{14}$

Sesenta y una y cinco décimas.

Ejercicio $\PageIndex{15}$

Quinientos once y cuatro milésimas.

Responder: 511.004

Ejercicio $\PageIndex{16}$

Treinta y tres y doce diez milésimas.

Ejercicio $\PageIndex{17}$

Novecientos cuarenta y siete milésimas.

Responder: 0.947

Ejercicio $\PageIndex{18}$

Dos millonésimas.

Ejercicio $\PageIndex{19}$

Setenta y cien milésimas.

Responder: 0.00071

Ejercicio $\PageIndex{20}$

Uno y diez diez millonésimas.

Problemas de la calculadora
Para los siguientes 10 problemas, realice cada división usando una calculadora. Después escribe el decimal resultante usando palabras.

Ejercicio $\PageIndex{21}$

$3 \div 4$

Responder: setenta y cinco centésimas

Ejercicio $\PageIndex{22}$

$1 \div 8$

Ejercicio $\PageIndex{23}$

$4 \div 10$

Responder: cuatro décimas

Ejercicio $\PageIndex{24}$

$2 \div 5$

Ejercicio $\PageIndex{25}$

$4 \div 25$

Responder: dieciséis centésimas

Ejercicio $\PageIndex{26}$

$1 \div 50$

Ejercicio $\PageIndex{27}$

$3 \div 16$

Responder: mil ochocientos setenta y cinco diez milésimas

Ejercicio $\PageIndex{28}$

$15 \div 8$

Ejercicio $\PageIndex{29}$

$11 \div 20$

Responder: cincuenta y cinco centésimas

Ejercicio $\PageIndex{30}$

$9 \div 40$

Ejercicios para revisión

Ejercicio $\PageIndex{31}$

Redondear 2,614 al diez más cercano.

Responder: 2610

Ejercicio $\PageIndex{32}$

¿Es 691.428.471 divisible por 3?

Ejercicio $\PageIndex{33}$

Determinar el numerador faltante.

$\dfrac{3}{14} = \dfrac{?}{56}$

Responder: 12

Ejercicio $\PageIndex{34}$

Encuentra $\dfrac{3}{16}$ de $\dfrac{32}{39}$

Ejercicio $\PageIndex{35}$

Encuentra el valor de $\sqrt{\dfrac{25}{81}} + (\dfrac{2}{3})^2 + \dfrac{1}{9}$

Responder: $\dfrac{10}{9}$ o $1 \dfrac{1}{9}$

Dígitos a la derecha de la posición de unos

Fracciones decimales

Lectura de fracciones decimales

Escribir fracciones decimales

Ejercicios

Ejercicios para revisión

Support Center

How can we help?