20.4: El mayor factor común
- Page ID
- 161908
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Método de factorización
En los dos últimos tipos de problemas, conocíamos uno de los factores y pudimos determinar el otro factor a través de la división. Supongamos, ahora, se nos da el producto sin ningún factor. Nuestro problema es encontrar los factores, si es posible. Este procedimiento y los dos procedimientos anteriores se basan en la propiedad distributiva.
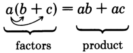
Utilizaremos la propiedad distributiva en reversa.
\(\underbrace{a b+a c}_{\text {product }}=\underbrace{a(b+c)}_{\text {factors }}\)
Notamos que en el producto,\(a\) es común a ambos términos. (De hecho,\(a\) es un factor común de ambos términos.) Dado que\(a\) es común a ambos términos, lo factorizaremos y escribiremos
\(a ()\)
Ahora necesitamos determinar qué colocar dentro de los paréntesis. Este es el procedimiento de la sección anterior. Dividir cada término del producto por el factor conocido\(a\).
\(\dfrac{ab}{a} = b\)y\(\dfrac{ac}{a} = c\)
Así,\(b\) y\(c\) son los términos requeridos del otro factor. Por lo tanto,
\(ab + ac = a(b+c)\)
Al factorizar un monomio a partir de un polinomio, buscamos factores que no solo son comunes a cada término del polinomio sino factores que tienen estas propiedades:
- Los coeficientes numéricos son los mayores coeficientes numéricos comunes.
- Las variables poseen los mayores exponentes comunes a todas las variables.
Mayor factor común
Un factor monomial que cumple con los dos requisitos anteriores se denomina el mayor factor común del polinomio.
Conjunto de Muestras A
Factor\(3x - 18\)
El mayor factor común es\(3\).
\ (\ begin {array} {ras a la izquierda}
3x-18&=&3\ cdot x - 3\ cdot 6&\ text {Factor de salida} 3\\
3x-18&=&3 () &\ text {Divide cada término del producto por} 3\\
&&&\ dfrac {3x} {3} = x\ text {y}\ dfrac {-18} {3} -6\\
&&&\ texto {( Intenta realizar esta división mentalmente.} \\
3x-18&=&3 (x-6)
\ end {array}\)
Factor\(9x^3+18x^2+27x\)
Observe que\(9x\) es el mayor factor común.
\(9x^3 + 18x^2 + 27x = 9x \cdot x^2 + 9x \cdot 2x + 9x \cdot 3\). Factor hacia fuera\(9x\) Dividir\(9x\)
\(9x^3 + 18x^2 + 27x = 9x()\) mentalmente en cada término del producto\)
\(9x^3 + 18x^2 + 27x = 9x(x^2+2x+3)\)
Factor\(10x^2y^3 - 20xy^4 - 35y^5\).
Observe que\(5y^3\) es el mayor factor común. Facturar hacia fuera\(5y^3\).
\(10x^2y^3-20xy^4-35y^5 = 5y^3()\)
\(5y^3\)Dividir mentalmente en cada término del producto y colocar los cocientes resultantes dentro del ().
\(10x^2y^3-20xy^4-35y^5=5y^3(2x^2-4xy-7y^2)\)
Factor\(-12x^5 + 8x^3 - 4x^2\).
Vemos que el mayor factor común es\(-4x^2\).
\(-12x^5 + 8x^3 - 4x^2 = -4x^2()\)
\(-4x^2\)Dividiendo mentalmente en cada término del producto, obtenemos
\(-12x^5 + 8x^3 - 4x^2 = -4x^2(3x^3 - 2x + 1\)
Conjunto de práctica A
Factor\(4x−48\).
- Responder
-
\(4(x−12)\)
Factor\(6y^3 + 24y^2 + 36y\)
- Responder
-
\(6y(y^2 + 4y + 6)\)
Factor\(10a^5b^4 - 14a^4b^5-8b^6\)
- Responder
-
\(2b^4(5a^5 - 7a^4b - 4b^2\)
Factor\(-14m^4 + 28m^2 - 7m\)
- Responder
-
\(-7m(2m^2 - 4m + 1\)
Considera este problema: factor\(Ax+Ay\). Seguramente,\(Ax+Ay=A(x+y)\). Sabemos desde el comienzo de nuestro estudio del álgebra que las letras representan cantidades únicas. También sabemos que una cantidad que ocurre dentro de un conjunto de paréntesis debe considerarse como una sola cantidad. Supongamos que la letra\(A\) está representando la cantidad\((a+b)\). Entonces tenemos
\(Ax + Ay = A(x+y)\)
\((a+b)x + (a+b)y = (a+b)(x+y)\)
Cuando observamos la expresión
\((a+b)x + (a+b)y\)
notamos que\((a+b)\) es común a ambos términos. Como es común, lo factorizamos.
\((a+b)( )\)
Como es habitual, determinamos qué colocar dentro de los paréntesis dividiendo cada término del producto por\((a+b)\).
\(\dfrac{(a+b)x}{(a+b)} = x\)y\(\dfrac{(a+b)y}{(a+b)} = y\)
Se trata de un precursor del factoring que se realizará en la Sección 5.4.
Conjunto de Muestras B
Factor\((x−7)a+(x−7)b\).
Observe que\((x-7)\) es el mayor factor común. Facturar hacia fuera\((x-7)\).
\((x-7)a + (x-7)b = (x-7)( )\)
Entonces,\(\dfrac{(x-7)a}{(x-y)} = a \text{ and } \dfrac{(x-7)b}{(x-7)} = b\)
\((x-7)a+(x-7)b = (x-7)(a+b)\)
Factor\(3x^2(x+1)-5x(x+1)\).
Observe que\(x\) y\((x+1)\) son comunes a ambos términos. Factorializarlos. Realizaremos esta factorización dejando\(A = x(x+1)\). Entonces tenemos
\(3xA-5A = A(3x-5)\)
Pero\(A = x(x+1)\), entonces
\(3x^2(x+1)-5x(x+1) = x(x+1)(3x-5)\)
Set de práctica B
Factor\((y+4)a+(y+4)b\).
- Responder
-
\((y+4)(a+b)\)
Factor\(8m^3(n-4) - 6m^2(n-4)\)
- Responder
-
\(2m^2(n-4)(4m-3)\)
Ejercicios
Para los siguientes problemas, factorizar los polinomios.
\(9a+18\)
- Responder
-
\(9(a+2)\)
\(6a+24\)
\(8b+12\)
- Responder
-
\(4(2b+3)\)
\(16x+12\)
\(4x−6\)
- Responder
-
\(2(2x−3)\)
\(8x−14\)
\(21y−28\)
- Responder
-
\(7(3y−4)\)
\(16f−36\)
\(12x^2 + 18x\)
- Responder
-
\(6x(2x+3)\)
\(10y^2 + 15y\)
\(8y^2 + 18\)
- Responder
-
\(2(4y^2 + 9)\)
\(7x^2 - 21\)
\(3y^2 - 6\)
- Responder
-
\(3(y^2 - 2)\)
\(2x^2-2\)
\(6y^2-6y\)
- Responder
-
\(6y(y−1)\)
\(ax^2-a\)
\(by^2 + b\)
- Responder
-
\(b(y^2 + 1)\)
\(7by^2 + 14b\)
\(5a^2x^2 + 10x\)
- Responder
-
\(5x(a^2x + 2)\)
\(24ax^2 + 28a\)
\(10x^2 + 5x - 15\)
- Responder
-
\(5(2x^2 + x - 3)\)
\(12x^2 - 8x - 16\)
\(15y^3 - 24y + 9\)
- Responder
-
\(3(5y^3 - 8y + 3)\)
\(ax^2 + ax + a\)
\(by^3 + by^2 + by + b\)
- Responder
-
\(b(y^3 + y^2 + y + 1)\)
\(2y^2 + 6y + 4xy\)
\(9x^2 + 6xy + 4x\)
- Responder
-
\(x(9x+6y+4)\)
\(30a^2b^2 + 40a^2b^2 + 50a^2b^2\)
\(13x^2y^5c - 26x^2y^5c - 39x^2y^5\)
- Responder
-
\(13x^2y^5(-c-3)\)
\(-4x^2-12x-8\)
\(-6y^3 - 8y^2 - 14y + 10\)
- Responder
-
\(-2(3y^3 + 4y^2 + 7y - 5)\)
\(Ab+Ac\)
\(Nx+Ny\)
- Contestar
-
\(N(x+y)\)
\(Qx+Qy\)
\(Ax−Ay\)
- Contestar
-
\(A(x−y)\)
\((x+4)b+(x+4)c\)
\((x−9)a+(x−9)b\)
- Contestar
-
\((x−9)(a+b)\)
\((2x+7)a+(2x+7)b\)
\((9a−b)w−(9a−b)x\)
- Contestar
-
\((9a−b)(w−x)\)
\((5−v)X+(5−v)Y\)
\(3x^5y^4 - 12x^3y^4 + 27x^5y^3 - 6x^2y^6\)
- Contestar
-
\(3x^2y^3(x^3y - 4xy + 9x^3-2y^3)\)
\(8a^3b^{15} + 24a^2b^{14} + 48a^3b^6 - 20a^3b^7 + 80a^4b^6 - 4a^3b^6 - 4a^3b^7 + 4a^2b\)
\(-8x^3y^2 - 3x^3y^2 + 16x^4y^3 + 2x^2y\)
- Contestar
-
\(-x^2y(11xy-16x^2y^2-2)\)
Ejercicios para la revisión
Una cantidad más\(21\)% más de esa cantidad es\(26.25\). ¿Cuál es la cantidad original?
Resuelve la ecuación\(6(t−1)=4(5−s)\) si\(s=2\).
- Contestar
-
\(t=3\)
Dado que\(4a^3\) es un factor de\(8a^3 - 12a^2\), encontrar el otro factor.