21.6: Graficar ecuaciones en forma de pendiente-intercepción
( \newcommand{\kernel}{\mathrm{null}\,}\)
Uso de la pendiente y la intercepción para graficar una línea
Cuando se da una ecuación lineal en la forma general,ax+by=c, observamos que un enfoque gráfico eficiente fue el método de intercepción. Dejamosx=0 y calculamos el valor correspondiente dey, luego lety=0 y calculamos el valor correspondiente dex.
Cuando una ecuación se escribe en la forma pendiente-intercepcióny=mx+b,, también hay formas eficientes de construir la gráfica. Una forma, pero menos eficiente, es elegir dos o tresx valores y calcular para encontrar losy valores correspondientes. Sin embargo, los cálculos son tediosos, consumen mucho tiempo y pueden generar errores. Otra forma, el método que se indica a continuación, hace uso de la pendiente y lay -intercepción para graficar la línea. Es rápido, sencillo y no implica cálculos.
- Trazar lay -intercepción(0, b).
- Determinar otro punto usando la pendiente m.
- Dibuja una línea a través de los dos puntos.
Recordemos que definimos la pendientem como la relacióny2−y1x2−x1. El numeradory2−y1 representa el número de unidades quey cambia y el denominadorx2−x1 representa el número de unidades quex cambia. Supongamosm=pq. Entoncesp es el número de unidades quey cambia yq es el número de unidades quex cambia. Dado que estos cambios ocurren simultáneamente, comience con su lápiz en lay -intercepción, muevap las unidades en la dirección vertical apropiada y luego muevaq las unidades en la dirección horizontal apropiada. Marcar un punto en esta ubicación.
Conjunto de Muestras A
Grafica las siguientes líneas.
y=34x+2
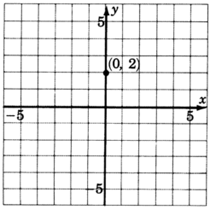
1. Ely -intercepto es el punto(0,2). Así, la línea cruza las2 unidadesy del eje por encima del origen. Marcar un punto en(0,2).
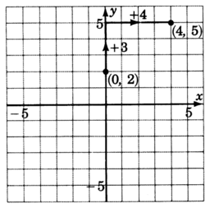
2. La pendiente,m, es34. Esto significa que si empezamos en algún punto de la línea y movemos nuestras3 unidades de lápiz hacia arriba y luego4 las unidades a la derecha, volveremos a estar en la línea. Empezar en un punto conocido, lay -intercepción(0, 2). Mueva3 las unidades hacia arriba, luego mueva4 las unidades a la derecha. Marcar un punto en esta ubicación. (Tenga en cuenta también que\ dfrac {3} {4} =\ dfrac {-3} {-4}\). Esto significa que si empezamos en algún punto de la línea y movemos nuestras3 unidades de lápiz hacia abajo y4 las unidades a la izquierda, volveremos a estar en la línea. Tenga en cuenta también eso34=341. Esto significa que si empezamos en algún punto de la línea y nos movemos a la1 unidad derecha, tendremos que subir34 unidad para volver a la línea.)
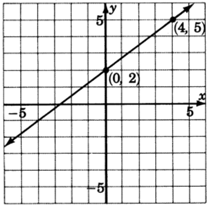
3. Dibuja una línea a través de ambos puntos.
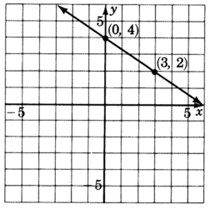
y=−12x+72
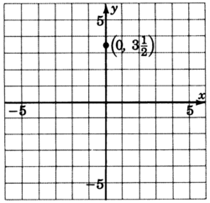
1. Ely -intercepto es el punto(0,72). Así, la línea cruza las72 unidadesy del eje por encima del origen. Marcar un punto(0,72), o(0,312).
2. La pendiente,m, es−12. Podemos escribir−12 como−12. Así, partimos en un punto conocido, lay -intercepción(0,312), nos desplazamos hacia abajo una unidad (debido a la−1), luego movemos2 las unidades a la derecha. Marcar un punto en esta ubicación.
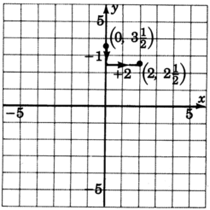
3. Dibuja una línea a través de ambos puntos.
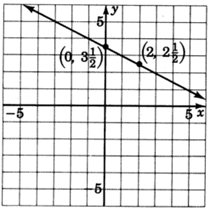
y=25x
1. Podemos poner esta ecuación en pendiente-intercepción explícita escribiéndola comoy=25x+0.
Ely -intercepto está en el punto(0,0), el origen. Esta línea va justo por el origen.
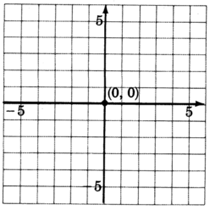
2. La pendiente,m, es25. Comenzando por el origen, subimos2 unidades, luego nos movemos a las5 unidades correctas. Marcar un punto en esta ubicación.
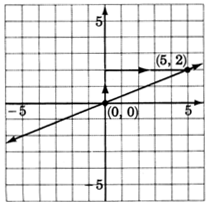
3. Dibuja una línea a través de los dos puntos.
y=2x−4
1. Ely -intercepto es el punto(0,−4). Así, la línea cruza las4 unidadesy del eje por debajo del origen. Marcar un punto en(0,−4).
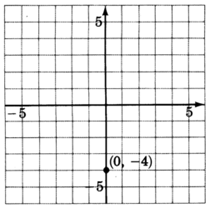
2. La pendiente,m, es2. Si escribimos la pendiente como una fracción2=21,, podemos leer cómo hacer los cambios. Comience en el punto conocido(0,−4), mueva hacia arriba2 las unidades, luego mueva la1 unidad derecha. Marcar un punto en esta ubicación.
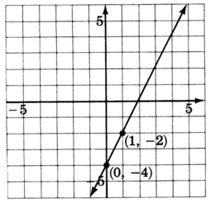
3. Dibuja una línea a través de los dos puntos.
Conjunto de práctica A
Utilice lay -intercepción y la pendiente para graficar cada línea.
y=−23+4

- Responder
-
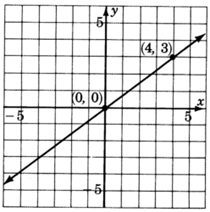
y=34x

- Responder
-
Ejercicios
Para los siguientes problemas, grafica las ecuaciones.
y=23+1

- Responder
-
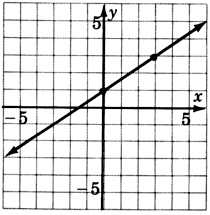
y=14x−2

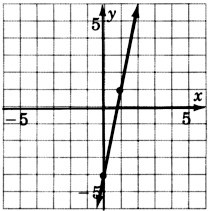
y=5x−4

- Responder
-
y=−65−3

y=32−5

- Responder
-
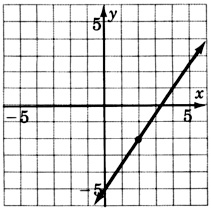
y=15x+2

y=−83+4

- Responder
-
y=−103+6

y=1x−4

- Responder
-
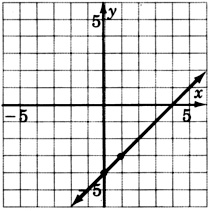
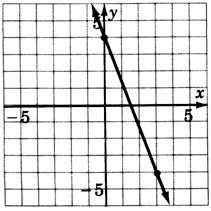
y=−2x+1

y=x+2

- Responder
-
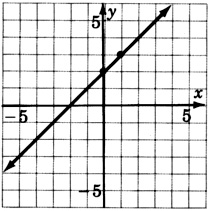
y=35x

y=−43

- Responder
-
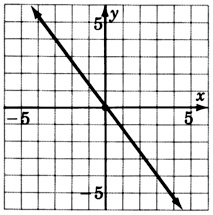
y=x

y=−x

- Responder
-
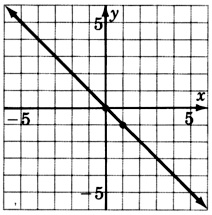
3y−2x=−3

6x+10y=30

- Responder
-
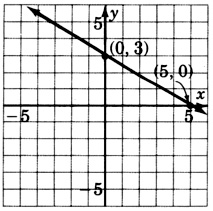
x+y=0

Ejercicios para revisión
Resolver la desigualdad2−4x≥x−3
- Responder
-
x≤1
Graficar la desigualdady+3>1.

Grafica la ecuacióny=−2.

- Responder
-
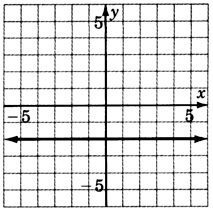
Determinar la pendiente yy -intercepción de la línea−4y−3x=16.
Encuentra la pendiente de la línea que pasa por los puntos(−1, 5) y(2, 3).
- Responder
-
m=−23


