22.5: ¿Cuánto en cada Grupo? (Parte 1)

Lección

Veamos los problemas de división que nos ayudan a encontrar el tamaño de un grupo.

Ejercicio\(\PageIndex{1}\): Inventing a Situation

1. Piense en una situación con una pregunta que pueda ser representada por la ecuación\(12\div\frac{2}{3}=?\) Describa la situación y la pregunta.
2. Comercia descripciones con tu pareja y responde a la pregunta de tu pareja.

Ejercicio\(\PageIndex{2}\): How Much in One Batch?

Para hacer 5 lotes de galletas, se requieren 10 tazas de harina. Considera la pregunta: ¿Cuántas tazas de harina requiere cada lote?

Podemos escribir ecuaciones y dibujar un diagrama para representar esta situación.

\(5\cdot ?=10\)

\(10\div 5=?\)

Figura\(\PageIndex{1}\): Un diagrama de cinta de 5 partes iguales con cada parte etiquetada con un signo de interrogación. Encima del diagrama hay un corsé que representa el total etiquetado 10 tazas. Debajo del diagrama, se indican 5 tirantes donde cada tirante contiene 1 parte igual. El primero de los tirantes está etiquetado como 1 lote.

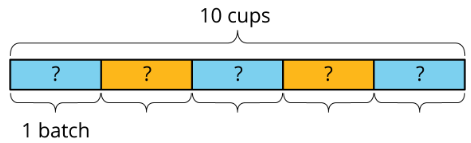
Esto nos ayuda a ver que cada lote requiere 2 tazas de harina.

Para cada pregunta, escribe una ecuación de multiplicación y una ecuación de división, dibuja un diagrama y encuentra la respuesta.

1. Para hacer 4 lotes de cupcakes, se necesitan 6 tazas de harina. ¿Cuántas tazas de harina se necesitan para 1 lote?
2. Para hacer\(\frac{1}{2}\) lote de rollos, se necesitan\(\frac{5}{4}\) tazas de harina. ¿Cuántas tazas de harina se necesitan para 1 lote?
3. Dos tazas de harina hacen\(\frac{2}{3}\) lote de pan. ¿Cuántas tazas de harina hacen 1 lote?

Ejercicio\(\PageIndex{3}\): One Container and One Section of Highway

Aquí hay tres diagramas de cinta que representan situaciones sobre el llenado de recipientes de agua.

Figura\(\PageIndex{2}\): 3 diagramas de barras de fracción. Diagrama 1, diagrama 2 y diagrama 3. Diagrama 1 2 partes iguales. 1 y la fracción 1 sobre 2 partes sombreadas. 1 parte etiquetada cantidad desconocida y 1 contenedor. Uno y la fracción 1 sobre 2 partes etiquetadas 15 tazas. Diagrama 2, 2 partes iguales. Ambas partes sombreadas. 1 parte etiquetada cantidad desconocida y 1 contenedor. Total etiquetado 15 tazas. Diagrama 3, 3 partes iguales. 1 parte sombreada y etiquetada 15 tazas. Total etiquetó la cantidad desconocida y 1 contenedor.

Haga coincidir cada situación con un diagrama y use el diagrama para ayudarlo a responder la pregunta. Después, escribe una ecuación de multiplicación y una ecuación de división para representar la situación.

1. Tyler vertió un total de 15 tazas de agua en 2 botellas de igual tamaño y llenó cada botella. ¿Cuánta agua había en cada botella?
2. Kiran vertió un total de 15 tazas de agua en jarras de igual tamaño y llenó\(1\frac{1}{2}\) jarras. ¿Cuánta agua había en la jarra llena?
3. Se necesitan 15 tazas de agua para llenar el\(\frac{1}{3}\) balde. ¿Cuánta agua se necesita para llenar 1 cubeta?

Aquí hay diagramas de cinta que representan situaciones sobre la limpieza de tramos de carretera.

Figura\(\PageIndex{3}\): 3 diagramas de barras de fracción. Diagrama 1, diagrama 2 y diagrama 3. Diagrama 1, 2 partes iguales ambas sombreadas. 1 parte etiquetada cantidad desconocida y 1 sección. Total etiquetó la fracción 3 sobre 4 millas. Diagrama 2, 3 partes iguales. 1 parte sombreada. 1 parte etiquetada la fracción 3 sobre 4 millas. Total etiquetada cantidad desconocida y 1 sección. Diagrama 3, 2 partes iguales. Uno y la fracción 1 sobre 2 partes sombreadas. 1 parte etiquetada cantidad desconocida y 1 sección. Uno y la fracción 1 sobre 2 partes etiquetaron la fracción 3 sobre 4 millas.

Haga coincidir cada situación con un diagrama y use el diagrama para ayudarlo a responder la pregunta. Después, escribe una ecuación de multiplicación y una ecuación de división para representar la situación.

4. La clase de Priya ha adoptado dos tramos iguales de una carretera para mantenerse limpia. La longitud combinada es\(\frac{3}{4}\) de una milla. ¿Cuánto dura cada sección?
5. La clase de Lin también ha adoptado algunos tramos de carretera para mantenerse limpios. Si\(1\frac{1}{2}\) las secciones tienen una\(\frac{3}{4}\) milla de largo, ¿cuánto dura cada sección?
6. Una escuela ha adoptado un tramo de carretera para mantenerse limpio. Si\(\frac{1}{3}\) de la sección tiene una\(\frac{3}{4}\) milla de largo, ¿cuánto dura la sección?

¿Estás listo para más?

Para hacer un conjunto ternario Cantor:

• Comience con un diagrama de cinta de longitud 1 unidad. Este es el paso 1.
• Color en el tercio medio del diagrama de cinta. Este es el paso 2.
• Haga lo mismo con cada segmento restante que no esté coloreado. Este es el paso 3.
• Sigue repitiendo este proceso.

Figura\(\PageIndex{4}\): Tres diagramas de cinta de igual longitud, paso 1, paso 2, y paso 3. el paso 1 es una barra blanca sólida. el paso 2 se divide en 3 partes iguales. La segunda parte está sombreada azul. el paso 3 se divide en 9 partes iguales. La segunda, cuarta, quinta, sexta y octava partes están sombreadas en azul.

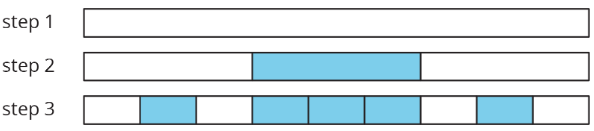
1. ¿Cuánto del diagrama se colorea después del paso 2? ¿Paso 3? ¿Paso 10?
2. Si continúas con este proceso, ¿cuánto del diagrama de cinta colorearás?
3. ¿Se te ocurre un proceso diferente que te dará un resultado similar? Por ejemplo, colorea el primer quinto en lugar del tercio medio de cada tira.

Resumen

A veces sabemos la cantidad para múltiples grupos, pero no sabemos cuánto hay en un solo grupo. Podemos usar la división para averiguarlo.

Por ejemplo, si 5 personas comparten\(8\frac{1}{2}\) libras de cerezas por igual, ¿cuántas libras de cerezas recibe cada persona?

Figura\(\PageIndex{5}\): Diagrama de barras de fracción. 5 partes iguales. Cada parte etiquetada cantidad desconocida. 1 parte etiquetada 1 persona. Total etiquetado 8 libras y media y 5 personas.

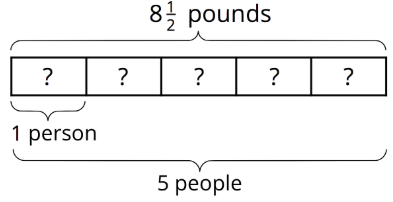
Podemos representar esta situación con una ecuación de multiplicación y una ecuación de división:

\(5\cdot ?=8\frac{1}{2}\)

\(8\frac{1}{2}\div 5=?\)

\(8\frac{1}{2}\div 5\)se puede escribir como\(\frac{17}{2}\div 5\). Dividir por 5 equivale a multiplicar por\(\frac{1}{5}\), y\(\frac{17}{2}\cdot\frac{1}{5}=\frac{17}{10}\). Esto significa que cada persona recibe\(1\frac{7}{10}\) libras.

Otras veces, sabemos la cantidad para una fracción de un grupo, pero no sabemos el tamaño de un grupo entero. También podemos usar la división para averiguarlo.

Por ejemplo, Jada sirvió 5 tazas de té helado en una jarra y llenó\(\frac{2}{3}\) de la jarra. ¿Cuántas tazas de té helado llenan toda la jarra?

Figura\(\PageIndex{6}\): Un diagrama de barras de fracción. 3 partes iguales. 2 partes sombreadas y etiquetadas 5 tazas y la fracción 2 sobre 3 jarra. Cantidad total etiquetada de tazas desconocidas y 1 jarra.

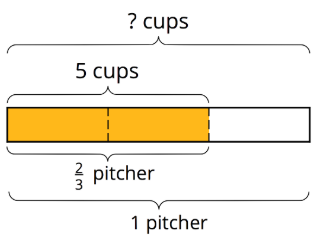
Podemos representar esta situación con una ecuación de multiplicación y una ecuación de división:

\(\frac{2}{3}\cdot ?=5\)

\(5\div\frac{2}{3}=?\)

El diagrama puede ayudarnos a razonar sobre la respuesta. Si\(\frac{2}{3}\) de una jarra es 5 tazas, entonces\(\frac{1}{3}\) de una jarra es la mitad de 5, que es\(\frac{5}{2}\). Debido a que hay 3 tercios en 1 entero, habría\((3\cdot\frac{5}{2})\) o\(\frac{15}{2}\) tazas en una jarra entera. Podemos verificar nuestra respuesta multiplicando:\(\frac{2}{3}\cdot\frac{15}{2}=\frac{30}{6}\), y\(\frac{30}{6}=5\).

Observe que en el primer ejemplo, el número de grupos es mayor que 1 (5 personas) y en el segundo, el número de grupos es menor que 1 (\(\frac{2}{3}\)de un lanzador), pero las ecuaciones de división y multiplicación para ambas situaciones tienen las mismas estructuras.

Practica

Ejercicio\(\PageIndex{4}\)

Para cada situación, complete el diagrama de cinta para representar y responder a la pregunta.

1. Mai ha recogido 1 taza de fresas para un pastel, que es suficiente para\(\frac{3}{4}\) del pastel. ¿Cuántas tazas necesita para todo el pastel?

Figura\(\PageIndex{7}\)

2. Priya ha recogido\(1\frac{1}{2}\) tazas de frambuesas, que es suficiente para\(\frac{3}{4}\) de un pastel. ¿Cuántas tazas necesita para todo el pastel?

Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{5}\)

Considera el problema: Tyler pintó yardas\(\frac{9}{2}\) cuadradas de área de pared con\(3\) galones de pintura. ¿Cuántos galones de pintura se necesitan para pintar cada yarda cuadrada de pared?

1. Escribir ecuaciones de multiplicación y división para representar la situación.
2. Dibuja un diagrama para representar y responder a la pregunta.

Ejercicio\(\PageIndex{6}\)

Considera el problema: Después de caminar a una\(\frac{1}{4}\) milla de su casa, Han está\(\frac{1}{3}\) de camino a la escuela. ¿Cuál es la distancia entre su casa y la escuela?

1. Escribir ecuaciones de multiplicación y división para representar esta situación.
2. Complete el diagrama para representar y responder a la pregunta.

Figura\(\PageIndex{9}\)

Ejercicio\(\PageIndex{7}\)

Aquí hay una ecuación de división:\(\frac{4}{5}\div\frac{2}{3}=?\)

1. Escribir una ecuación de multiplicación que corresponda a la ecuación de división.
2. Dibuja un diagrama para representar y responder a la pregunta.

(De la Unidad 4.2.4)

Ejercicio\(\PageIndex{8}\)

Considera el problema: Un conjunto de libros que son cada uno de 1.5 pulgadas de ancho se están organizando en una estantería de 36 pulgadas de ancho. ¿Cuántos libros caben en la repisa?

1. Escribir ecuaciones de multiplicación y división para representar la situación.
2. Encuentra la respuesta. Dibuja un diagrama, si es necesario.
3. Usa la ecuación de multiplicación para verificar tu respuesta.

(De la Unidad 4.1.3)

Ejercicio\(\PageIndex{9}\)

1. Sin calcular, ordene los cocientes desde los más pequeños o mayores.
   \[\begin{array}{ccccc}{56\div 8}&{\qquad}&{56\div 8,000,000}&{\qquad}&{56\div 0.000008}\end{array}\nonumber\]
2. Explica cómo decidiste el orden de las tres expresiones.
3. Encuentra un número\(n\) para que\(56\div n\) sea mayor que 1 pero menor que 7.

(De la Unidad 4.1.1)