Saltar al contenido principal
LibreTexts Español

27.1: Uso de diagramas para representar sumas y restas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119673

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Representemos suma y resta de decimales.

    Ejercicio\(\PageIndex{1}\): Changing Values

    1. Aquí hay un rectángulo.
    clipboard_e64dfd2bace2749f4a0679af93039eec6.png
    Figura\(\PageIndex{1}\)

    ¿Qué número representa el rectángulo si cada cuadrado pequeño representa:

    1. \(1\)
    2. \(0.1\)
    3. \(0.01\)
    4. \(0.001\)
    1. Aquí hay una plaza.
    clipboard_e1a3609fdc488dc65c37c88f2c5834f25.png
    Figura\(\PageIndex{2}\)

    ¿Qué número representa el cuadrado si cada rectángulo pequeño representa:

    1. \(10\)
    2. \(0.1\)
    3. \(0.00001\)

    Ejercicio\(\PageIndex{2}\): Squares and Rectangles

    Puede estar familiarizado con los bloques de base diez que representan unos, decenas y cientos. Aquí hay algunos diagramas que usaremos para representar unidades digitales de base diez. Un cuadrado grande representa 1 uno. Un rectángulo representa 1 décima. Un cuadrado pequeño representa 1 centésima.

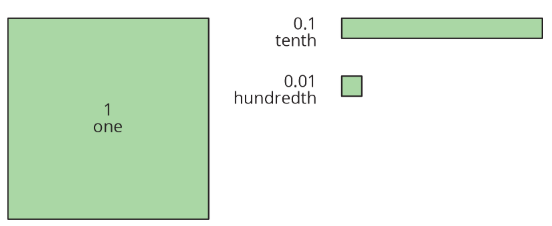
    clipboard_e0f37a36fec8f91704814049c75a4d888.png
    Figura\(\PageIndex{3}\)

    El applet tiene herramientas que crean cada uno de los bloques de base diez.

    Seleccione una herramienta Bloquear y luego haga clic en la pantalla para colocarla.

    Uno

    clipboard_ea626a7486226f7ca0d649e505b475eb4.png
    Figura\(\PageIndex{4}\)

    Décimo

    clipboard_eda808aeaebeb36f021f1185f5c6dbab7.png
    Figura\(\PageIndex{5}\)

    centésima

    clipboard_e3f3b03b59d8377f8d9d33acc93ef30b2.png
    Figura\(\PageIndex{6}\)

    Haga clic en la herramienta Mover cuando haya terminado de elegir bloques.

    clipboard_e661f9ff658e7304ceb21f52916661c02.png
    Figura\(\PageIndex{7}\)
    1. Aquí está el diagrama que dibujó Priya para representar 0.13. Dibuja un diagrama diferente que represente 0.13. Explica por qué tu diagrama y el diagrama de Priya representan el mismo número.
    clipboard_e6737fde5572089b48b4b81b35ee5ecfe.png
    Figura\(\PageIndex{8}\)
    1. Aquí está el diagrama que Han dibujó para representar 0.25. Dibuja un diagrama diferente que represente 0.25. Explica por qué tu diagrama y el diagrama de Han representan el mismo número.
    clipboard_e995775f9ef3ccde660454421a113f711.png
    Figura\(\PageIndex{9}\)
    1. Para cada uno de estos números, dibuje o describa dos diagramas diferentes que lo representen.
      1. \(0.1\)
      2. \(0.02\)
      3. \(0.43\)
    2. Utilice diagramas de unidades de base diez para representar las siguientes sumas y encontrar sus valores. Piensa en cómo podrías usar la menor cantidad de unidades posible para representar cada número.
      1. \(0.03+0.05\)
      2. \(0.06+0.07\)
      3. \(0.4+0.7\)

    Ejercicio\(\PageIndex{3}\): Finding Sums in Different Ways

    1. Aquí hay dos formas de calcular el valor de\(0.26+0.07\). En el diagrama, cada rectángulo representa\(0.1\) y cada cuadrado representa\(0.01\).
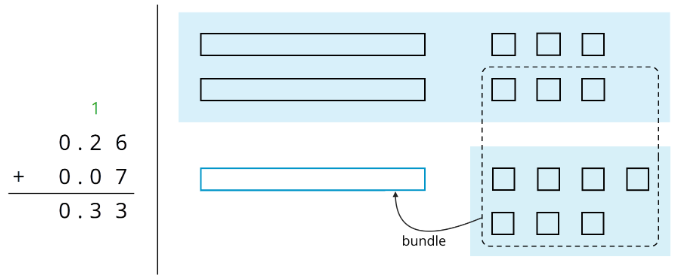
    clipboard_e90d7f599c0cdb2c443e8705667c0aa9b.png
    Figura\(\PageIndex{10}\): Diagrama de dos estrategias utilizadas para calcular la expresión de suma. La estrategia izquierda, una ecuación vertical de 0 punto 2 6 más 0 punto 0 7 da como resultado 0 punto 3 3. Un 1 está escrito arriba del 2 en la columna décimas. La estrategia correcta, un diagrama base diez. Se indican 2 rectángulos grandes y 6 cuadrados pequeños. Directamente debajo, los cuadrados son 7 cuadrados pequeños adicionales indicados. Un círculo discontinuas contiene 10 de los cuadrados pequeños con una flecha, etiquetada como haz, apuntando a un tercer rectángulo grande. El tercer rectángulo se dibuja debajo de los otros dos rectángulos grandes existentes.

    Usa lo que sabes sobre las unidades de base diez y la adición de números de base diez para explicar:

    1. Por qué diez cuadrados pueden ser “agrupados” en un rectángulo.
    2. Cómo se refleja este “agrupamiento” en el cómputo.

    El applet tiene herramientas que crean cada uno de los bloques de base diez. Seleccione una herramienta Bloquear y luego haga clic en la pantalla para colocarla.

    Uno

    clipboard_ea626a7486226f7ca0d649e505b475eb4.png
    Figura\(\PageIndex{11}\)

    Décimo

    clipboard_eda808aeaebeb36f021f1185f5c6dbab7.png
    Figura\(\PageIndex{12}\)

    centésima

    clipboard_e3f3b03b59d8377f8d9d33acc93ef30b2.png
    Figura\(\PageIndex{13}\)

    Haga clic en la herramienta Mover cuando haya terminado de elegir bloques.

    clipboard_e661f9ff658e7304ceb21f52916661c02.png
    Figura\(\PageIndex{14}\)
    1. Encuentra el valor de\(0.38+0.69\) dibujando un diagrama. ¿Puedes encontrar la suma sin agrupar? ¿Sería útil agrupar algunas piezas? Explica tu razonamiento.
    2. Calcular\(0.38+0.69\). Consulta tu cálculo con tu diagrama en la pregunta anterior.
    3. Encuentra cada suma. El cuadrado más grande representa\(1\), el rectángulo representa\(0.1\) y el cuadrado más pequeño representa\(0.01\).
    clipboard_ecf7fed8004397e714c918246118104c0.png
    Figura\(\PageIndex{15}\)
    clipboard_e8d6932139679f97982bc3466f68204e9.png
    Figura\(\PageIndex{16}\)

    ¿Estás listo para más?

    Una tierra lejana y mágica utiliza joyas para su sistema de trueque. Las joyas son valoradas y clasificadas en orden de su rareza. Cada joya vale 3 veces la joya inmediatamente por debajo de ella en el ranking. El ranking es rojo, naranja, amarillo, verde, azul, índigo y violeta. Entonces una joya roja vale 3 joyas naranjas, una joya verde vale 3 joyas azules, y así sucesivamente.

    1. Si tuvieras 500 joyas violetas y quisieras comerciar para que llevaras la menor cantidad de joyas posible, ¿qué joyas tendrías?
    2. Supongamos que tienes 1 joya naranja, 2 joyas amarillas y 1 joya índigo. Si te dan 2 joyas verdes y 1 amarilla, ¿cuál es la menor cantidad de joyas que podrían representar el valor de las joyas que tienes?

    Ejercicio\(\PageIndex{4}\): Representing Subtraction

    1. Aquí hay diagramas que representan diferencias. Las piezas retiradas están marcadas con Xs. El rectángulo más grande representa 1 décima. Para cada diagrama, escriba una expresión de resta numérica y determine el valor de la expresión.
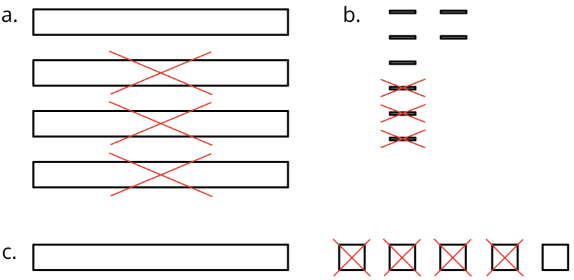
    clipboard_e144fc3539cb1cd9e7daae09f2a715485.png
    Figura\(\PageIndex{17}\)
    1. Expresar cada resta en palabras.
      1. \(0.05-0.02\)
      2. \(0.024-0.003\)
      3. \(1.26-0.14\)
    2. Encuentra cada diferencia dibujando un diagrama y calculando con números. Asegúrese de que las respuestas de ambos métodos coincidan. Si no, revisa tu diagrama y tu cálculo numérico.
      1. \(0.05-0.02\)
      2. \(0.024-0.003\)
      3. \(1.26-0.14\)

    Resumen

    Los diagramas de base diez representan colecciones de unidades de base diez: decenas, unas, décimas, centésimas, etc. Podemos utilizarlos para ayudarnos a entender las sumas de decimales.

    Supongamos que estamos encontrando\(0.08+0.13\). Aquí hay un diagrama donde un cuadrado representa\(0.01\) y un rectángulo (compuesto por diez cuadrados) representa\(0.1\).

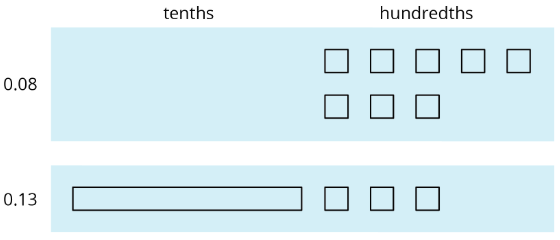
    clipboard_e94dd9542172ac2ba6ba9228f7c74e03d.png
    Figura\(\PageIndex{18}\): Diagrama de base diez. Primera fila, 0 punto 0 8. No hay barras en la columna de décimas. 8 cuadrados pequeños en la columna de centésimas. Segunda fila, 0 punto 13. 1 varilla en la columna de décimas. 3 cuadrados pequeños en la columna de centésimas.

    Para encontrar la suma, podemos “agrupar” (o componer) 10 centésimas como 1 décima.

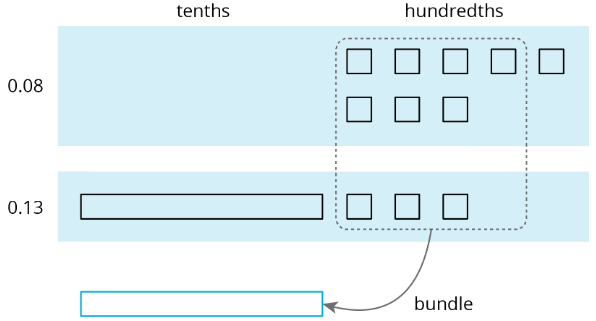
    clipboard_e2b110099200716852b0ed9a6458d328f.png
    Figura\(\PageIndex{19}\): Diagrama de base diez. Primera fila, 0 punto 0 8. No hay barras en la columna de décimas. 8 cuadrados pequeños en la columna de centésimas. Segunda fila, 0 punto 13. 1 varilla en la columna de décimas. 3 cuadrados pequeños en la columna de centésimas. Se dibuja un cuadrado alrededor de los 10 cuadrados pequeños. Se dibuja una flecha hacia una barra décimas fuera del diagrama. La flecha está etiquetada como paquete.

    Ahora tenemos 2 décimas y 1 centésima, entonces\(0.08+0.13=0.21\).

    clipboard_e15bedcdff0739f4022db8a8c35d7cac5.png
    Figura\(\PageIndex{20}\)

    También podemos utilizar el cálculo vertical para encontrar\(0.08+0.13\).

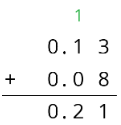
    clipboard_e72e485a9fdc4912786c99dbd1cce5734.png
    Figura\(\PageIndex{21}\)

    Observe cómo esta representación también muestra que 10 centésimas están agrupadas (o compuestas) como 1 décima.

    Esto funciona para cualquier decimal. Supongamos que estamos encontrando\(0.008+0.013\). Aquí hay un diagrama donde representa un pequeño rectángulo\(0.001\).

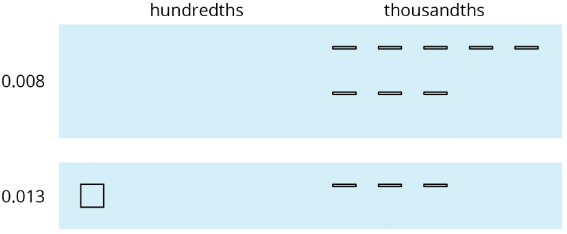
    clipboard_e2e59955bda7ca14a961de4600b95b311.png
    Figura\(\PageIndex{22}\): Diagrama de base diez. Primera fila, 0 punto 0 0 8. No hay cuadrados en la columna de centésimas. 8 rectángulos pequeños en la columna milésimas. Segunda fila, 0 punto 0 1 3. 1 cuadrado pequeño en la columna de centésimas. 3 rectángulos pequeños en la columna milésimas.

    Podemos “agrupar” (o componer) 10 milésimas como 1 centésima.

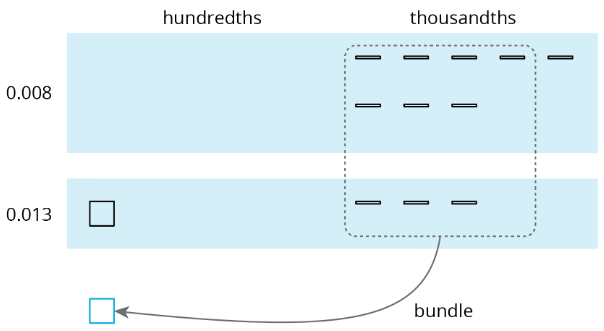
    clipboard_e799fac3436c94c235667802a07ea9fa4.png
    Figura\(\PageIndex{23}\): Diagrama de base diez. Primera fila, 0 punto 0 0 8. No hay cuadrados en la columna de centésimas. 8 rectángulos pequeños en la columna milésimas. Segunda fila, 0 punto 0 1 3. 1 cuadrado pequeño en la columna de centésimas. 3 rectángulos pequeños en la columna milésimas. Se dibuja un cuadrado alrededor de los 10 rectángulos pequeños. Se dibuja una flecha hacia un pequeño cuadrado fuera del diagrama. La flecha está etiquetada como paquete.

    La suma es de 2 centésimas y 1 milésima.

    clipboard_e649c4f26c0d3eaf192e048b93522951d.png
    Figura\(\PageIndex{24}\)

    Aquí hay un cálculo vertical de\(0.008+0.013\).

    clipboard_ead6ccf81f4526bdca3ea5aef18a32ff4.png
    Figura\(\PageIndex{25}\): Adición vertical. Primera línea. 0 punto 0 13. Segunda línea. Más 0 punto 0 0 8. Línea horizontal. Tercera línea. 0 punto 0 2 1. Por encima del 1 en la primera línea está 1.

    Practica

    Ejercicio\(\PageIndex{5}\)

    Utilice la clave dada para responder a las preguntas.

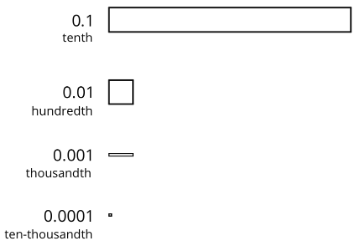
    clipboard_ef0d0c7bf3d7302146207a233afa10193.png
    Figura\(\PageIndex{26}\): Figuras de base diez. 1 rectángulo grande etiquetado, 0 punto 1, décimo, 1 cuadrado etiquetado, 0 punto 0 1, centésima, 1 rectángulo pequeño etiquetado, 0 punto 0 0 1, milésima, 1 cuadrado pequeño etiquetado, 0 punto 0 0 0 1, diezmilésima.
    1. ¿Qué número representa este diagrama?
    clipboard_eb07444fb4b89c6995489b3e3bb53d49a.png
    Figura\(\PageIndex{27}\)
    1. Dibuja un diagrama que represente\(0.216\).
    2. Dibuja un diagrama que represente\(0.304\).

    Ejercicio\(\PageIndex{6}\)

    Aquí hay diagramas que representan\(0.137\) y\(0.284\).

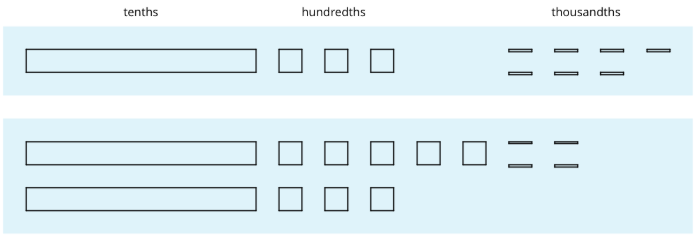
    clipboard_e11e492d92702b6eb266d51ccdba43878.png
    Figura\(\PageIndex{28}\): Dos diagramas de base diez que representan 0 punto 1 3 7 y 0 punto 2 8 4. Primer diagrama, 1 rectángulo etiquetado, décimas, 3 cuadrados etiquetados, centésimas, 7 rectángulos pequeños etiquetados, milésimas. Segundo diagrama, 2 rectángulos etiquetados, décimas, 8 cuadrados etiquetados, centésimas, 4 rectángulos pequeños etiquetados, milésimas.
    1. Utilice el diagrama para encontrar el valor de\(0.137+0.284\). Explica tu razonamiento.
    2. Calcular la suma verticalmente.
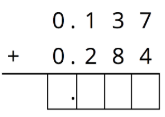
    clipboard_e32f68c574beee581892e31933cd2cee4.png
    Figura\(\PageIndex{29}\)
    1. ¿Cómo fue tu\(0.137+0.284\) razonamiento sobre lo mismo con los dos métodos? ¿En qué se diferenciaba?

    Ejercicio\(\PageIndex{7}\)

    Para los dos primeros problemas, circule el cálculo vertical donde se alinean dígitos del mismo tipo. Después, termine el cálculo y encuentre la suma. Para los dos últimos problemas, encuentra la suma usando cálculo vertical.

    1. \(3.25+1\)
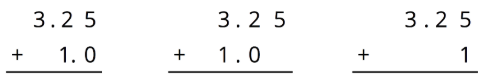
    clipboard_e40c8e9fc998257896c11792eb0d64da2.png
    Figura\(\PageIndex{30}\): 3 cálculos verticales de 3 punto 2 5 más 1. Primer cálculo, 3 punto 2 5 más 1 punto 0, el punto decimal para 1 punto 0 se desplaza un lugar a la derecha. Segundo cálculo, 3 punto 2 5 más 1 punto 0, los decimales están alineados. Tercer cálculo, 3 punto 2 5 más 1, el 1 se desplaza dos lugares a la derecha.
    1. \(0.5+1.15\)
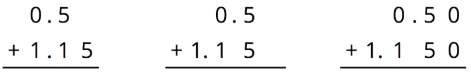
    clipboard_e53e010d711add9d6cacdfb0154986177.png
    Figura\(\PageIndex{31}\): 3 cálculos verticales de 0 punto 5 más 1 punto 1 5. Primer cálculo, 0 punto 5 más 1 punto 1 5, se alinean los decimales. Segundo cálculo, 0 punto 5 más 1 punto 1 5, punto decimal de 1 punto 1 5 desplazado un lugar a la izquierda. Tercer cálculo, 0 punto 5 0 más 1 punto 1 5 0, punto decimal de 1 punto 1 5 0 desplazó un lugar a la izquierda.
    1. \(10.6+1.7\)
    2. \(123+0.2\)

    Ejercicio\(\PageIndex{8}\)

    Andre ha estado practicando sus datos matemáticos. Ahora puede completar 135 hechos de multiplicación en 90 segundos.

    1. Si Andre responde preguntas a un ritmo constante, ¿cuántos hechos puede responder por segundo?
    2. Noé también trabaja a un ritmo constante, y puede completar 75 hechos en 1 minuto. ¿Quién trabaja más rápido? Explica o muestra tu razonamiento.

    (De la Unidad 2.3.4)

    27.1: Uso de diagramas para representar sumas y restas is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by LibreTexts.