Saltar al contenido principal
LibreTexts Español

46.3: Locura Rectangular

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    119839

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Lección

    Cortemos rectángulos.

    Ejercicio\(\PageIndex{1}\): Squares in Rectangles

    1. \(ABCD\)El rectángulo no es un cuadrado. \(ABEF\)El rectángulo es un cuadrado.
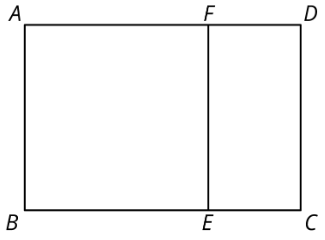
    clipboard_e23550736162f32faa498e41bed697692.png
    Figura\(\PageIndex{1}\)
    1. Supongamos que el segmento\(AF\) tenía 5 unidades de largo y el segmento\(FD\) de 2 unidades de largo ¿Cuánto tiempo\(AD\) sería el segmento?
    2. Supongamos que el segmento\(BC\) tenía 10 unidades de largo y el segmento\(BE\) 6 unidades de largo. ¿Cuánto tiempo\(EC\) sería el segmento?
    3. Supongamos que el segmento\(AF\) tenía 12 unidades de largo y el segmento\(FD\) 5 unidades de largo. ¿Cuánto tiempo\(FE\) sería el segmento?
    4. Supongamos que el segmento\(AD\) tenía 9 unidades de largo y el segmento\(AB\) 5 unidades de largo. ¿Cuánto tiempo\(F\) sería el segmento?
    1. \(JKXW\)El rectángulo se ha descompuesto en cuadrados.
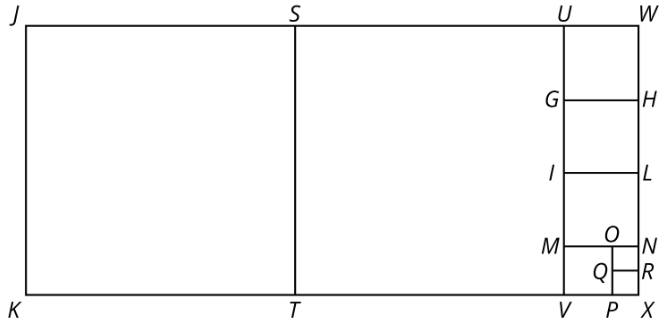
    clipboard_e2c8a0de1e728327c54c188682fcbd9d5.png
    Figura\(\PageIndex{2}\): Baldosas de rectángulo KXWJ con 2 cuadrados grandes, KJST y TSUV; 3 cuadrados medianos, GUWH, KGHL y MILN; 1 cuadrado pequeño, VMOP; y 2 cuadrados diminutos, QONR y PQRX. TSUV y KJST se apilan horizontalmente. El TSUV se encuentra a la derecha de KJST. GUWH, KGHL y MILN se apilan verticalmente. Los 3 están a la derecha del TSUV. VMOP está por debajo de MILN. QONR y PQRX se apilan verticalmente. Ambos están a la derecha del VMOP.

    \(JK\)El segmento tiene 33 unidades de largo y el segmento\(JW\) es de 75 unidades de largo. Encuentra las áreas de todos los cuadrados en el diagrama.

    1. \(ABCD\)El rectángulo es de 16 unidades por 5 unidades.
    clipboard_efc308d1ceffbfe83edbc62a1cddbe6b0.png
    Figura\(\PageIndex{3}\)
    1. En el diagrama, dibuja un segmento de línea que se descompone\(ABCD\) en dos regiones: un cuadrado que sea el más grande posible y un nuevo rectángulo.
    2. Dibuja otro segmento de línea que descomponga el nuevo rectángulo en dos regiones: un cuadrado que sea el más grande posible y otro nuevo rectángulo.
    3. Continúe hasta que\(ABCD\) el rectángulo esté completamente descompuesto en cuadrados.
    4. Enumere las longitudes laterales de todos los cuadrados en su diagrama.

    ¿Estás listo para más?

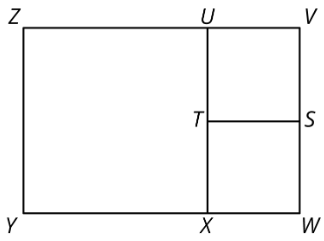
    clipboard_e951120ce85863529e32c03d691198ba5.png
    Figura\(\PageIndex{4}\): El rectángulo VWYZ se descompone en 3 cuadrados. YZUX es un cuadrado grande. UVTS y XTSW son dos cuadrados de igual tamaño que se apilan verticalmente. Ambos están a la derecha de YZUX.
    1. El diagrama muestra que el rectángulo se\(VWYZ\) ha descompuesto en tres cuadrados. ¿Cuáles podrían ser las longitudes laterales de este rectángulo?
    2. ¿Cuántas longitudes de lado diferentes puedes encontrar para el rectángulo\(VWYZ\)?
    3. ¿Cuáles son algunas reglas para las posibles longitudes laterales del rectángulo\(VWYZ\)?

    Ejercicio\(\PageIndex{2}\): More Rectangles, More Squares

    1. Dibuja un rectángulo que sea de 21 unidades por 6 unidades.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que el diagrama muestre que tu rectángulo original se ha descompuesto completamente en cuadrados.
      2. ¿Cuántos cuadrados de cada tamaño hay en tu diagrama?
      3. ¿Cuál es la longitud lateral del cuadrado más pequeño?
    2. Dibuja un rectángulo que sea de 28 unidades por 12 unidades.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que el diagrama muestre que tu rectángulo original se ha descompuesto en cuadrados.
      2. ¿Cuántos cuadrados de cada tamaño hay en tu diagrama?
      3. ¿Cuál es la longitud lateral del cuadrado más pequeño?
    3. Escribe cada una de estas fracciones como un número mixto con el numerador y denominador más pequeños posibles:
      1. \(\frac{16}{5}\)
      2. \(\frac{21}{6}\)
      3. \(\frac{28}{12}\)
    4. ¿Qué tienen que ver los problemas de fracción con los problemas de descomposición de rectángulos anteriores?

    Ejercicio\(\PageIndex{3}\): Finding Equivalent Fractions

    1. Dibuja con precisión un rectángulo que sea de 9 unidades por 4 unidades.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que tu rectángulo original se haya descompuesto completamente en cuadrados.
      2. ¿Cuántos cuadrados de cada tamaño hay?
      3. ¿Cuáles son las longitudes laterales del último cuadrado que dibujaste?
      4. Escribir\(\frac{9}{4}\) como un número mixto.
    2. Dibuja con precisión un rectángulo que sea de 27 unidades por 12 unidades.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que tu rectángulo original se haya descompuesto completamente en cuadrados.
      2. ¿Cuántos cuadrados de cada tamaño hay?
      3. ¿Cuáles son las longitudes laterales del último cuadrado que dibujaste?
      4. Escribir\(\frac{27}{12}\) como un número mixto.
      5. Compara el diagrama que dibujaste para este problema y el del problema anterior. ¿Cómo son iguales? ¿En qué se diferencian?
    3. ¿Cuál es el mayor factor común de 9 y 4? ¿Cuál es el mayor factor común de 27 y 12? ¿Qué tiene esto que ver con tus diagramas de rectángulos descompuestos?

    ¿Estás listo para más?

    Hemos visto algunos ejemplos de inclinaciones de rectángulo. Un mosaico significa una forma de cubrir completamente una forma con otras formas, sin huecos ni superposiciones. Por ejemplo, aquí hay un mosaico de rectángulo\(KXWJ\) con 2 cuadrados grandes, 3 cuadrados medianos, 1 cuadrado pequeño y 2 cuadrados diminutos.

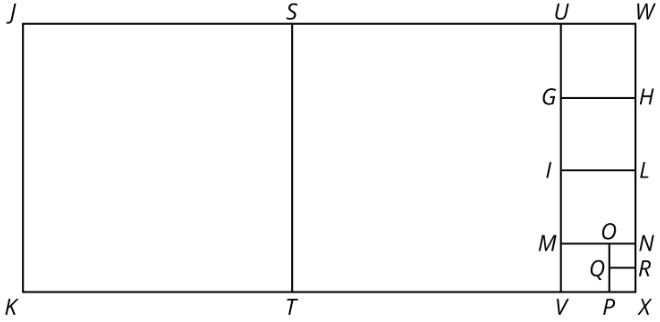
    clipboard_e2d2642e7ec156acf26d2b9e5cb671513.png
    Figura\(\PageIndex{5}\): Baldosas de rectángulo KXWJ con 2 cuadrados grandes, KJST y TSUV; 3 cuadrados medianos, GUWH, KGHL y MILN; 1 cuadrado pequeño, VMOP; y 2 cuadrados diminutos, QONR y PQRX. TSUV y KJST se apilan horizontalmente. El TSUV se encuentra a la derecha de KJST. GUWH, KGHL y MILN se apilan verticalmente. Los 3 están a la derecha del TSUV. VMOP está por debajo de MILN. QONR y PQRX se apilan verticalmente. Ambos están a la derecha del VMOP.

    Algunos de los cuadrados utilizados para recubrir este rectángulo tienen el mismo tamaño.

    ¿Podría ser posible colocar un rectángulo con cuadrados donde los cuadrados son todos de diferentes tamaños?

    Si crees que es posible, encuentra tal rectángulo y tal mosaico. Si crees que no es posible, explica por qué no es posible.

    Ejercicio\(\PageIndex{4}\): It's All About Fractions

    1. Dibuja con precisión un rectángulo de 37 por 16. (Utilice papel cuadrigrafiado, si es posible.)
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que tu rectángulo original se haya descompuesto completamente en cuadrados.
      2. ¿Cuántos cuadrados de cada tamaño hay?
      3. ¿Cuáles son las dimensiones de la última plaza que dibujaste?
      4. ¿Con qué tiene que ver esto\(2+\frac{1}{3+\frac{1}{5}}\)?
    2. Considera un rectángulo de 52 por 15.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que tu rectángulo original se haya descompuesto completamente en cuadrados.
      2. Escribe una fracción igual a esta expresión:\(3+\frac{1}{2+\frac{1}{7}}\).
      3. Observe algunas conexiones entre el rectángulo y la fracción.
      4. ¿Cuál es el mayor factor común de 52 y 15?
    3. Considera un rectángulo de 98 por 21.
      1. En tu rectángulo, dibuja un segmento de línea que descomponga el rectángulo en un nuevo rectángulo y un cuadrado que sea lo más grande posible. Continúa hasta que tu rectángulo original se haya descompuesto completamente en cuadrados.
      2. Escribe una fracción igual a esta expresión:\(4+\frac{1}{1+\frac{7}{14}}\).
      3. Observe algunas conexiones entre el rectángulo y la fracción.
      4. ¿Cuál es el mayor factor común de 98 y 21?
    4. Considera un rectángulo de 121 por 38.
      1. Utilice el proceso de descomposición en cuadrados para escribir una fracción continua para\(\frac{121}{38}\). Verificar que funcione.
      2. ¿Cuál es el mayor factor común de 121 y 38?

    This page titled 46.3: Locura Rectangular is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by Illustrative Mathematics via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.