1.4. Campos escalares diferenciables
( \newcommand{\kernel}{\mathrm{null}\,}\)
\newcommand{\conj}[1]{\overline{}[1]}}
\newcommand{\vector}[1]{\vec{\textbf {}[1]}}}
\newcommand{\abs}[1]{\left\vert {#1} \right\vert}}
\newcommand{\vectork}{\vector{\mathbf{k}})
\newcommand{\vectorrp}{\vector r}\,{}'}
\newcommand{\vectorrs}{\vector r}\,{}''}
\newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}
\newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}
\newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}
\newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}
\newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}
\newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}
\newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}
\newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}
\newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}
\newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}
\newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}
\newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}
\newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}
\newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}
La construcción del plano tangente
Dados f:U→R, un campo escalar continuo de dos variables, y (a,b) un punto interior de U, sea P=(a,b,c) el punto correspondiente en la gráfica de f, la superficie z=f(x,y), de manera que c=f(a,b). ¿Existe el plano tangente a la gráfica de f en P y, en ese caso, cuál es su ecuación?
Un plano tangente razonable debería cumplir las siguientes tres condiciones intuitivas:
- La primera es la extensión al caso de dos variables de la propiedad que tienen las ordenadas de los puntos de la recta tangente a la gráfica de una función de una variable de ser buenas aproximaciones de los valores correspondientes de la propia función cerca del punto de tangencia. Por eso, pediremos que si (x,y,z) es un punto del plano tangente y (x,y) está cerca de (a,b), entonces z debe estar cerca de f(x,y).
- La segunda es una propiedad geométrica adicional: si C es una curva contenida en la superficie z=f(x,y) que pasa por el punto P, entonces la recta tangente a C en P debe quedarse contenida en el plano tangente.
- La tercera es que la construcción del plano tangente debe proporcionarnos los planos tangentes que ya conocemos en los casos de superficies como las esferas, los cilindros o los conos.

Vector normal y plano tangente.
Para construir el plano tangente, sabiendo que debe pasar por el punto P, basta con determinar un vector ⇀n que sea perpendicular a dicho plano. Para ello, usaremos la interpretación geométrica de las derivadas parciales vista en la Sección 1.3. Allí se construyeron sobre la superficie gráfica de f las curvas C1 y C2 que se obtienen, respectivamente, al cortar la superficie con los planos verticales y=b y x=a y vimos que los vectores tangentes a dichas curvas en P son, respectivamente, ⇀T1=(1,0,fx(a,b)) y ⇀T2=(0,1,fy(a,b)).
De acuerdo con la segunda condición descrita antes, las rectas tangentes R1 y R2 a las curvas C1 y C2 en el punto P deberían quedar contenidas en el plano tangente. Por tanto, un vector perpendicular al plano tangente debería ser ortogonal tanto a ⇀T1 como a ⇀T2, así que podríamos tomar como vector perpendicular su producto vectorial
⇀n(a,b)=⇀T1×⇀T2=(1,0,fx(a,b))×(0,1,fy(a,b))=(−fx(a,b),−fy(a,b),1).
Usando este vector como vector perpendicular, el plano tangente vendría dado por la ecuación
z=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b).
Ejemplo. Consideremos el punto P=(1,2,2) en la esfera x2+y2+z2=9. Sabemos que el plano tangente a la esfera en dicho punto es el que tiene como vector normal el radio-vector ⇀r=(1,2,2) del propio punto. Si cerca de P escribimos la ecuación de la esfera en la forma z=f(x,y)=√9−x2−y2 y calculamos las derivadas parciales obtenemos
fx(1,2)=−2x2√9−x2−y2(1,2)=−1/2fy(1,2)=−2y2√9−x2−y2(1,2)=−1
con lo que, según lo visto antes, el vector perpendicular es ⇀n(1,2)=(−(−1/2),−(−1),1)=(1/2,1,1) que, efectivamente, es paralelo a ⇀r=(1,2,2).
Observación. Aunque en el ejemplo de la esfera las cosas funcionan bien, la mera existencia de las derivadas parciales no basta para que, en el caso de un campo escalar continuo cualquiera, el plano dado por z=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b) sea un plano tangente satisfactorio. Pueden construirse ejemplos patológicos de campos para los que existen las derivadas parciales pero el plano que se obtiene con ellas no cumple condiciones geométricas deseables que hemos citado antes. Veamos un ejemplo de esta situación no deseable.
*Ejemplo patológico. Consideremos la superficie de ecuación z=f(x,y) siendo f el campo escalar
f(x,y)={2x2yx2+y2si (x,y)≠(0,0),0si (x,y)=(0,0).
Este campo escalar es continuo en todo el plano (véase el Ejercicio 4 de la Sección 1.1), así que tiene sentido plantearse cuál es plano tangente a la superficie z=f(x,y) en el origen (0,0). Para ello, calculamos las derivadas parciales
fx(0,0)=límx→0f(x,0)−f(0,0)x=0,fy(0,0)=límy→0f(0,y)−f(0,0)x=0,
con lo que la ecuación del plano tangente saldría z=0, o sea, el plano XY.
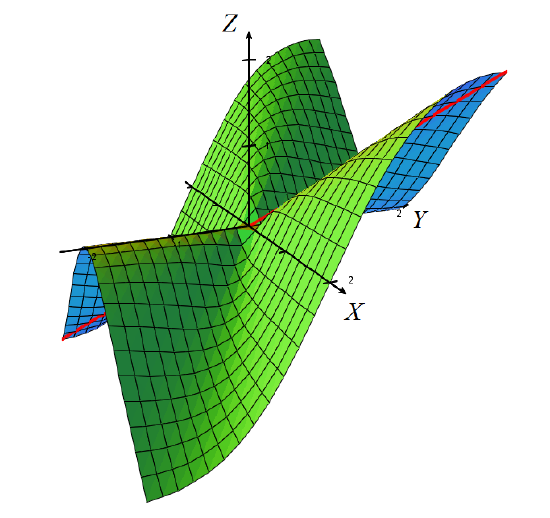
La superficie z=2x2y(x2+y2) y la recta x=y=z (en rojo)
Ahora bien, como se aprecia en el dibujo, cuando nos acercamos al origen por una dirección distinta a la del eje X o a la del eje Y, la superficie parece seguir una recta inclinada y no se pega al plano tangente cerca del origen. Por ejemplo, la recta dada por x=y=z está contenida en la superficie y pasa por el origen, por lo que debería estar contenida en el plano tangente z=0. Sin embargo, esto no ocurre, lo que va en contra de las condiciones intuitivas de qué propiedades debe tener un plano tangente descritas antes. (Véase el Ejercicio 7.)
Afortunadamente, este ejemplo se aleja de la situación habitual en las aplicaciones. Vamos a ver que en (casi) todos los casos de interés en las aplicaciones, el plano z=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b) sí cumple propiedades de aproximación y tangencia satisfactorias. La condición adicional esencial es que las derivadas parciales fx y fy sean también continuas, es decir, que f sea de clase C1.
Campo escalar diferenciable (2D)
Condición suficiente de diferenciabilidad. Sea f:U→R un campo escalar de clase C1 en U. Si (a,b) es un punto interior de U, entonces se cumple
lím(x,y)→(a,b)f(x,y)−[f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b)]√(x−a)2+(y−b)2=0
en cuyo caso se dice que el campo f es diferenciable en (a,b).
[Una demostración] [Es condición suficiente pero no necesaria]
Observemos que la expresión f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b) que aparece entre corchetes en el numerador es, precisamente, el valor de la coordenada z en la ecuación de (el candidato a) plano tangente a la superficie z=f(x,y) en el punto P=(a,b,f(a,b)).
Interpretación geométrica de la diferenciabilidad. Para funciones de una variable, escribamos la definición de derivada f′(a)=límx→af(x)−f(a)x−a en la siguiente forma equivalente
límx→af(x)−[f(a)+f′(a)(x−a)]|x−a|=0,
Esta igualdad nos dice que para x cerca de a, los valores de las ordenadas de la recta tangente y(x)=f(a)+f′(a)(x−a) se aproximan muy bien a los valores de la función f(x); mejor, de hecho, de que lo que se aproxima x al punto a.
Si en el cociente de la expresión anterior sustituimos en el numerador (señalado en rojo en la figura) la función f(x) por el campo f(x,y) y la ordenada y(x) de la recta tangente por la altura z(x,y) del candidato a plano tangente, y sustituimos en el denominador (señalado en verde en la figura) el valor absoluto |x−a| por la distancia euclídea ‖(x,y)−(a,b)‖=√(x−a)2+(y−b)2 en el plano, obtenemos precisamente la noción de campo escalar diferenciable. Es decir, si el campo f es diferenciable en el punto (a,b) entonces cerca de dicho punto los valores de la variable z en la ecuación del candidato a plano tangente z(x,y)=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b) se aproximan muy bien a los valores del campo f(x,y); mejor, de hecho, que lo que se aproxima (x,y) al punto (a,b).
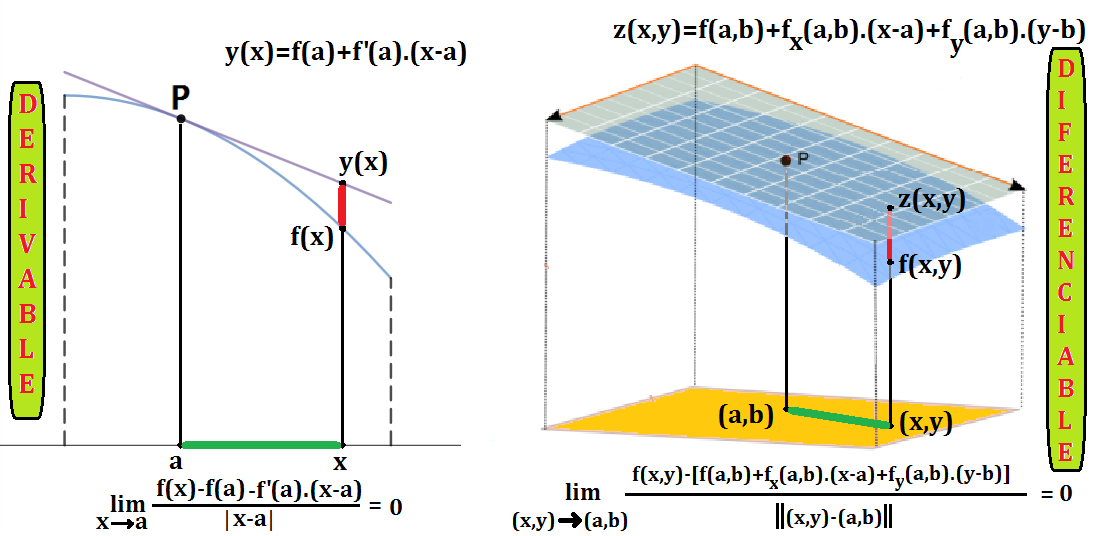
Derivabilidad (1D) frente a diferenciabilidad (2D)
Plano tangente
En otras palabras, que el campo sea de clase C1 garantiza, vía la diferenciabilidad, que se cumple la primera de las condiciones intuitivas que hemos formulado para que un plano pueda ser considerado un plano tangente razonable. Con respecto a la tercera, lo que hemos visto para el caso de un punto en una esfera podemos comprobarlo fácilmente también para un cono o un cilindro (véanse los Ejercicios 2 y 3). Finalmente, con respecto a la segunda condición, comprobaremos en la siguiente sección que si el campo es de clase C1 entonces el candidato a plano tangente en P contiene, efectivamente, a la recta tangente de cualquier curva regular en P contenida en la superficie gráfica z=f(x,y) del campo. Podemos entonces, con esta última salvedad, dar la siguiente definición.
Sean f:U→R campo escalar de clase C1 en su dominio U y (a,b) un punto interior de U, entonces el plano tangente a la gráfica de f en el punto P=(a,b,f(a,b)) es el plano dado por la ecuación
z=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b).
Vamos a explorar con más detenimiento el concepto de campo escalar diferenciable y, en particular, cómo podemos extender este concepto a campos que dependen de más variables.
El vector diferencial y la diferenciabilidad de un campo escalar
Supongamos que f(x,y) es un campo escalar de clase C1 y sea (a,b) un punto interior de su dominio. Si escribimos la propiedad de diferenciabilidad
lím(x,y)→(a,b)f(x,y)−[f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b)]√(x−a)2+(y−b)2=0.
de la siguiente manera
lím(x,y)→(a,b)f(x,y)−[f(a,b)+[fx(a,b),fy(a,b)]⋅(x−ay−b)]‖(x−a,y−b)‖=0
y comparamos esta expresión con la definición de derivada para funciones de una variable, observamos que el vector diferencial Df(a,b)=[fx(a,b),fy(a,b)] desempeña, en la definición de función diferenciable de dos variables, el papel correspondiente a f′(a) en la definición de derivada de una función de una variable.
Esto se ve aún más claramente si escribimos, por ejemplo, A=(a,b) y X=(x,y), entonces cuando el campo escalar f es diferenciable en A tenemos
límX→Af(X)−[f(A)+Df(A)⋅(X−A)]‖X−A‖=0.
Esto justifica que Df(A)=[fx(A),fy(A)] se llame vector diferencial de f en A. Veremos en el siguiente apartado que esta formulación tiene una extensión inmediata a campos en 3D.
La fórmula de los incrementos finitos (2D). En muchos textos, la definición de función diferenciable se escribe de una manera más adecuada para algunas aplicaciones. Si llamamos ε(x,y) al cociente
ε(x,y)=f(x,y)−[f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b)]√(x−a)2+(y−b)2
Entonces, decir que f es diferenciable en (a,b) es equivalente a decir que f se puede escribir como
f(x,y)=f(a,b)+fx(a,b)(x−a)+fy(a,b)(y−b)+ε(x,y)√(x−a)2+(y−b)2
donde ε(x,y) es una función tal que lím(x,y)→(a,b)ε(x,y)=0.
Si utilizamos los incrementos de las variables independientes Δx=x−a, Δy=y−b y el correspondiente incremento de la variable dependiente Δf=f(x,y)−f(a,b), tenemos
Δf=fx(a,b)Δx+fy(a,b)Δy+ε(x,y)√(Δx)2+(Δx)2
que se conoce como fórmula de los incrementos finitos y se suele usar para estimar cómo son los incrementos de la variable dependiente para incrementos pequeños de las variables independientes:
Δf≈∂f∂xΔx+∂f∂yΔy
donde Δx,Δy son suficientemente pequeños y la aproximación es de tamaño despreciable frente a ambos incrementos.
Campo escalar diferenciable (3D)
Si, para un campo escalar de tres variables, queremos seguir el mismo camino usado para definir el concepto de campo escalar diferenciable de dos variables, nos encontramos con una dificultad inicial: no es posible visualizar la noción de plano tangente a una superficie en R4. Sin embargo, dado un punto A=(a,b,c) interior al dominio de definición de un campo f(x,y,z), tiene perfecto sentido plantearse si, tomando X=(x,y,z), se cumple
límX→Af(X)−[f(A)+Df(A)⋅(X−A)]‖X−A‖=0.
siendo Df(A)=[fx(A),fy(A),fz(A)] el vector diferencial de f en A. Cuando se cumpla que, efectivamente, dicho límite es cero diremos que el campo escalar f es diferenciable en el punto A. Como en el caso bidimensional, puede probarse que si f es de clase C1 en su dominio, entonces f es diferenciable en todos los puntos del dominio (lo que también vale para campos escalares que dependen de más variables).
De forma similar al caso de dos variables, puede darse una fórmula de los incrementos finitos para campos de tres variables:
Δf=∂f∂xΔx+∂f∂yΔy+∂f∂zΔz+ε(x,y,z)√(Δx)2+(Δx)2+(Δz)2
siendo ε(x,y,z) una función tal que lím(x,y,z)→(a,b,z)ε(x,y,z)=0. Es decir Δf≈∂f∂xΔx+∂f∂yΔy+∂f∂zΔz.
Operaciones con campos diferenciables
Sean f,g:U→R campos escalares diferenciables en un punto A interior a U, α,β∈R y n∈N. Entonces los campos αf+βg, fg, fn y, si g(A)≠0, f/g son diferenciables en A y se verifica:
D(αf+βg)=αDf+βDg,D(fg)=fDg+gDf,Dfn=nfn−1Df,D(f/g)=gDf−fDgg2
donde las funciones y sus diferenciales están evaluados en A.
Observemos que entre estas operaciones falta el cambio de variables o, en otros términos, la operación de composición de funciones. A ella le dedicaremos la siguiente sección, donde veremos la regla de la cadena para campos escalares. Usando la regla de la cadena junto con las operaciones aritméticas que acabamos de ver se comprueba que la práctica totalidad de los campos escalares que aparecen en los ejemplos habituales y en las aplicaciones a la geometría y otras ciencias son diferenciables.
Ejercicios
Ejercicio 1. Halla las ecuaciones de los planos tangentes a la superficie z=f(x,y) en los puntos P=(0,0,f(0,0)) y Q=(1,−2,f(1,−2)).
(1)f(x,y)=cos(πx)+sen(πy)(2)f(x,y)=xy(3)f(x,y)=e−(x2+y2)/3(4)f(x,y)=x2+2xy+3y2(5)f(x,y)=5−x3+xy(6)f(x,y)=√64−x2(7)f(x,y)=x−3y+4(8)f(x,y)=x2+2xy−y2(9)f(x,y)=sen(π(x+y))(10)f(x,y)=log(1+2x2+3y2)(11)f(x,y)=5−x2−y2(12)f(x,y)=e−2x+cos(y)
Ejercicio 2. Si tenemos un punto P en un cilindro circular recto de radio R y situamos los ejes de coordenadas de manera que P=(0,0,R) y la ecuación del cilindro es x2+z2=R2, sabemos de la geometría elemental que el plano tangente al cilindro en P es z=R. Prueba que dicho plano coincide con el que se obtiene al aplicar al campo f(x,y)=√R2−x2 el procedimiento descrito en esta sección.
Ejercicio 3. Si en un cono circular recto tomamos un punto P distinto de su vértice y situamos los ejes de coordenadas de manera que P=(1,0,c) y la ecuación del cono es z2=c2(x2+y2), sabemos de la geometría elemental que el plano tangente al cilindro en P es z=cx. Prueba que dicho plano coincide con el que se obtiene al aplicar al campo f(x,y)=c√x2+y2 el procedimiento descrito en esta sección.
Ejercicio 4. Una máquina fabrica hojas de papel de tamaño A4 (210 mm ×297 mm) con una cierta holgura de ±1 mm en ambas dimensiones. Utiliza la fórmula de los incrementos finitos para hallar cómo pueden afectar estas holguras al área de la hoja.
Ejercicio 5. Los errores en la medición del radio y la altura de un cono circular recto son, respectivamente, del 2% y el 1%, ¿Cuáles son los errores aproximados de su volumen y su área?
Ejercicio 6. Los errores en la medida de dos resistencias un punto R1=200 ohmios y R2=500 ohmios son del 1% y el 3%, respectivamente. ¿Cuál es el error aproximado en la medida de la resistencia resultante si se conectan en serie? ¿y si se conectan en paralelo?
*Ejercicio 7. Prueba que el campo escalar del ejemplo patológico
f(x,y)={2x2yx2+y2si (x,y)≠(0,0),0si (x,y)=(0,0)
no es diferenciable en el origen. Para ello, calcula el límite cuando (x,y) tiende al origen a lo largo de una recta y=mx.

