1.5. La regla de la cadena
- Page ID
- 49583
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vector}[1]{\vec{\mathbf{#1}}}\)
\( \newcommand{\Disco}{\Bbb D}\)
\( \newcommand{\C}{\Bbb C}\)
\( \newcommand{\Q}{\Bbb Q}\)
\( \newcommand{\R}{\Bbb R}\)
\( \newcommand{\K}{\Bbb K}\)
\( \newcommand{\N}{\Bbb N}\)
\( \newcommand{\Z}{\Bbb Z}\)
\( \newcommand{\bo}{\textbf O}\)
\( \newcommand{\eps}{\varepsilon}\)
\( \newcommand{\la}{\lambda}\)
\( \newcommand{\om}{\omega}\)
\( \newcommand{\bmatriz}{\bmatrix \format \r&&\quad\r\\}\)
\( \newcommand{\bmatrize}{\bmatrix \format \c&&\quad\c\\}\)
\( \newcommand{\sep}{\, \equiv \,}\)
\( \newcommand{\xsep}{\quad \equiv \quad}\)
\( \newcommand{\xlsep}{\qquad \equiv \qquad}\)
\( \newcommand{\matriz}{\bmatrix\format\r&&\quad\r\\}\)
\( \newcommand{\endmatriz}{\endbmatrix}\)
\( \newcommand{\conj}[1]{\overline{}[1]}}\)
\( \newcommand{\vector}[1]{\vec{\textbf {}[1]}}}\)
\( \newcommand{\abs}[1]{\left\vert {#1} \right\vert}}\)
\( \newcommand{\norm}[1]{\left\Vert {#1}\right\Vert}\)
\( \newcommand{\bil}[2]{\left\langle {#1},{#2} \right\rangle}\)
\( \newcommand{\absbil}[2]{\abs{ \bil{#1}{#2} }}\)
\( \newcommand{\vectori}{\vector{\mathbf{\i}}}\)
\( \newcommand{\vectorj}{\vector{\mathbf{\j}}}\)
\( \newcommand{\vectork}{\vector{\mathbf{k}})\)
\( \newcommand{\vectorr}{\vector r}\)
\( \newcommand{\vectorrp}{\vector r}\,{}'}\)
\( \newcommand{\vectorrs}{\vector r}\,{}''}\)
\( \newcommand{\parteim}{\mathop{\text{Im}}\nolimits}\)
\( \newcommand{\partere}{\mathop{\text{Re}}\nolimits}\)
\( \newcommand{\sen}{\mathop{\text{sen}}\nolimits}\)
\( \newcommand{\sinc}{\mathop{\text{sinc}}\nolimits}\)
\( \newcommand{\sa}{\mathop{\text{sa}}\nolimits}\)
\( \newcommand{\senh}{\mathop{\text{senh}}\nolimits}\)
\( \newcommand{\arsenh}{\mathop{\text{arsenh}}\nolimits}\)
\( \newcommand{\arcosh}{\mathop{\text{arcosh}}\nolimits}\)
\( \newcommand{\Log}{\mathop{\text{Log}}\nolimits}\)
\( \newcommand{\Ln}{\mathop{\text{Ln}}\nolimits}\)
\( \newcommand{\Arg}{\mathop{\text{Arg}}\nolimits}\)
\( \newcommand{\arcsen}{\mathop{\text{arcsen}}\nolimits}\)
\( \newcommand{\arcos}{\mathop{\text{arccos}}\nolimits}\)
\( \newcommand{\arctg}{\mathop{\text{arctg}}\nolimits}\)
\( \newcommand{\ran}{\mathop{\text{ran}}\nolimits}\)
\( \newcommand{\maxe}{\mathop{\text{máx}}}\)
\( \newcommand{\mine}{\mathop{\text{mín}}}\)
\( \newcommand{\lime}{\mathop{\text{lím}}}\)
\( \newcommand{\lin}{\mathop{\text{lin}}\nolimits}\)
\( \newcommand{\inte}{\mathop{\text{int}}\nolimits}\)
\( \newcommand{\grad}{\mathop{\text{grad}}\nolimits}\)
\( \newcommand{\signo}{\mathop{\text{sig}}\nolimits}\)
\( \newcommand{\fl}{\mathop{\text{flot}}\nolimits}\)
\( \newcommand{\essup}{\mathop{\text{ess}\,\text{sup}}\nolimits}\)
\( \newcommand{\card}{\mathop{\text{card}}\nolimits}\)
\( \newcommand{\rot}{\mathop{\text{rot}}\nolimits}\)
\( \newcommand{\diver}{\mathop{\text{div}}\nolimits}\)
\( \newcommand{\volum}{\mathop{\text{vol}}\nolimits}\)
\( \newcommand{\Res}{\mathop{\text{Res}}\nolimits}\)
\( \newcommand{\grado}{\mathop{\text{gr}}\nolimits}\)
\( \newcommand{\dpar}[2]{\dfrac{\partial{#1}}{\partial{#2}}}\)
\( \newcommand{\dparx}[1]{\dfrac{\partial {#1}}{\partial x}}}\)
\( \newcommand{\dpary}[1]{\dfrac{\partial {#1}}{\partial y}}}\)
\( \newcommand{\dparz}[1]{\dfrac{\partial {#1}}{\partial z}}}\)
\( \newcommand{\dparr}[1]{\dfrac{\partial {#1}}{\partial r}}}\)
\( \newcommand{\dparth}[1]{\dfrac{\partial {#1}}{\partial \theta}}}\)
\( \newcommand{\dparxx}[1]{\dfrac{\partial^2 {#1}}{\partial x^2}}}\)
\( \newcommand{\dparyy}[1]{\dfrac{\partial^2 {#1}}{\partial y^2}}}\)
\( \newcommand{\dparxy}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial y}}}\)
\( \newcommand{\dparzz}[1]{\dfrac{\partial^2 {#1}}{\partial z^2}}}\)
\( \newcommand{\dparxz}[1]{\dfrac{\partial^2 {#1}}{\partial x \partial z}}}\)
\( \newcommand{\dparyz}[1]{\dfrac{\partial^2 {#1}}{\partial y \partial z}}}\)
\( \newcommand{\dpardos}[2]{\dfrac{\partial^2 {#1}}{\partial {#2}^2}}}\)
\( \newcommand{\dparcruz}[3]{\dfrac{\partial^2 {#1}}{\partial {#2} \partial {#3}}}\)
\( \newcommand{\dtan}[1]{ \dfrac{\partial {#1}}{\partial {\vector t}} }}\)
\( \newcommand{\dnormal}[1]{ \dfrac{\partial {#1}}{\partial {\vector n}} }}\)
La regla de la cadena para una variable independiente
La regla de la cadena permite calcular las derivadas parciales de un campo escalar cuando cambiamos las variables independientes, lo que, como en el caso de una variable, puede simplificar algunos cálculos (en el cálculo de integrales dobles y triples sobre todo, como veremos en el capítulo correspondiente) o proporcionar nuevas interpretaciones físicas cuando estudiamos modelos de las aplicaciones. En los siguientes capítulos analizaremos más a fondo los cambios de variables más importantes y otras implicaciones de la regla de la cadena.
Empezaremos por el caso más simple: tenemos un campo escalar \( f \) de dos o tres variables y ahora hacemos depender dichas variables de una nueva variable independiente \( t \); esto es lo que ocurre, por ejemplo, cuando nos interesa conocer el efecto de \( f \) sobre una curva. Estudiaremos después la regla de la cadena cuando cambiamos las variables independientes por otras nuevas.
Regla de la cadena para una variable independiente. Sea \( f \) un campo escalar de tres variables de clase \( C^1(U) \). Sean \( x=x(t) \), \( y=y(t) \), \( z=z(t) \) funciones derivables de \( t \) tales que los puntos \( \vecs {r}(t)=\bigl( x(t), y(t), z(t) \bigr) \) están en \( U \). Entonces \( \psi(t)=f\bigl( \vecs {r}(t) \bigr)=f \bigl( x(t),y(t), z(t) \bigr) \) es una función derivable y se verifica
\[ \psi'(t)=\dpar{f}x x'(t) + \dpar{f}y y'(t) +\dpar{f}z z'(t)= \begin{bmatrix} \dpar{f}x ,\, \dpar{f}y , \, \dpar{f}z \end{bmatrix} \cdot \begin{bmatrix} x'(t) \\ y'(t) \\ z'(t) \end{bmatrix} =Df\bigl( \vecs {r}(t) \bigr)\cdot \vecs {r}\,{}' (t). \notag\]
Si \( f \) depende de dos variables, entonces, suprimiendo la coordenada \( z \), la regla queda \( \psi'(t)=f_x x'(t)+f_y y'(t)\)
[Idea de una *demostración en (2D): Para calcular \(\psi'(t_0)\) sustituye \((x,y)\) por \((x(t),y(t))\) y \((a,b)\) por \((x(t_0), y(t_0))\) en la condición de diferenciabilidad (Dif) de la Sección 1.4. y usa el teorema del valor medio para estimar las diferencias \( x(t)-x(t_0)=x'(t_x)(t-t_0) \), \( y(t)-y(t_0) =y'(t_y)(t-t_0)\) para ciertos \(t_x,t_y\) entre \(t\) y \( t_0\).]
Propiedad de tangencia a las curvas del plano tangente a una superficie. Con la regla de la cadena podemos comprobar, como anunciamos en la sección anterior, que si \( f \) es un campo escalar de dos variables y \( f \) es de clase \(C^1\) en su dominio \( U \) y \( (a,b) \) es un punto interior de \( U \), entonces el plano tangente a la superficie \( z=f(x,y) \) en \( P=\bigl(a,b,f(a,b)\bigr) \) tiene la propiedad de contener las rectas tangentes a todas las curvas regulares contenidas en la superficie y que pasan por \( P \).
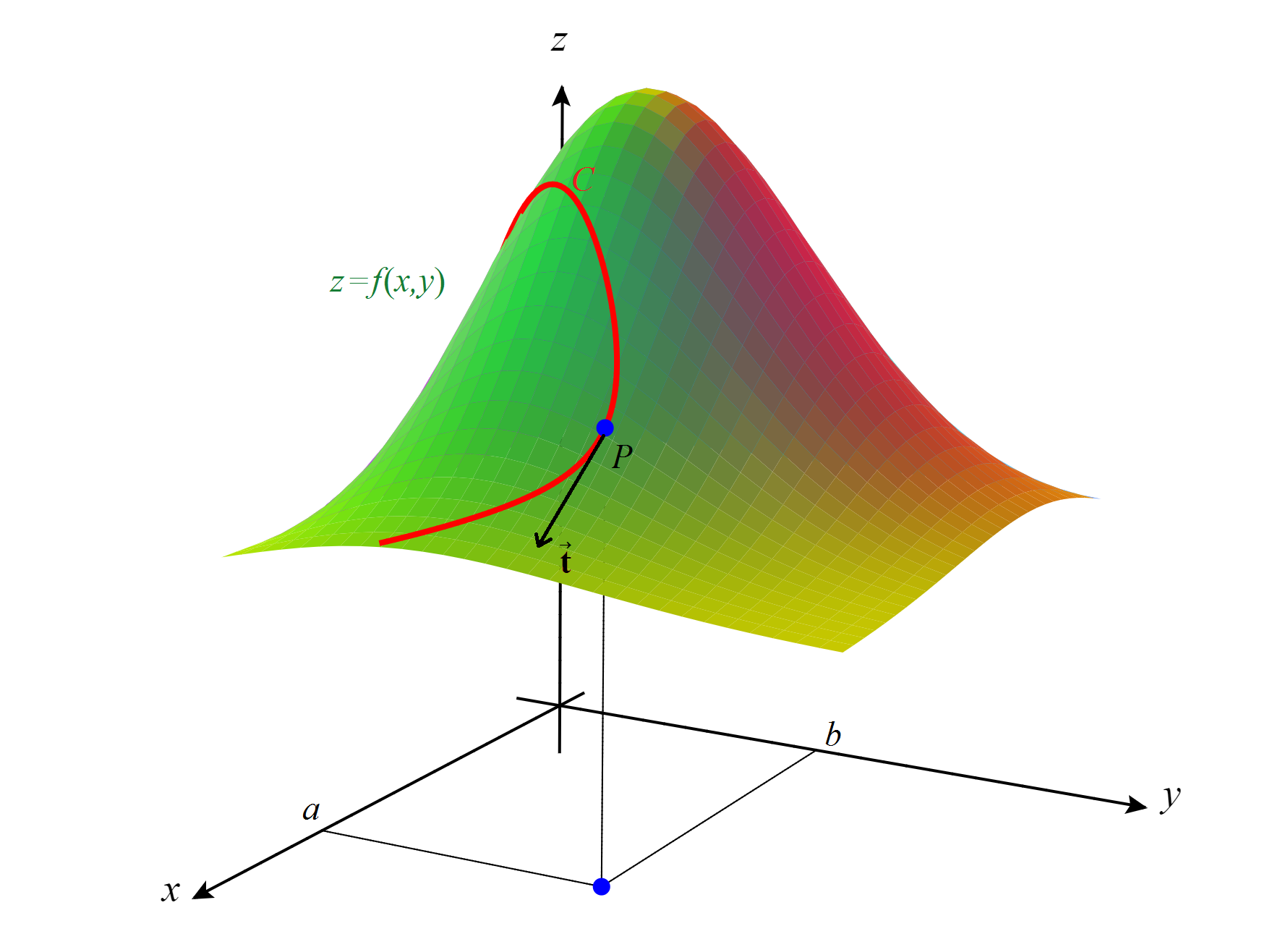
Curva \( C \) sobre una superficie \( z=f(x,y) \) y su vector tangente en \( P \).
Para ver esto, supongamos que \( C \) es una curva regular \( \vecs {r}(t)=\bigl( x(t), y(t), z(t) \bigr) \) totalmente contenida en la superficie \( z=f(x,y) \) y que pasa por el punto \( P=(a,b,f(a,b)) \). Tenemos entonces que \( z(t)=f\bigl(x(t),y(t)\bigr) \), porque la curva está contenida en la sperficie, y que \( a=x(t_0) \) y \( b=y(t_0) \) para algún valor \( t_0 \) porque la curva pasa por \( P \). Sabemos que \( \vecs t=\vecs {r}\,{}' (t_0) \) es un vector tangente a la curva \( C \) en \( P \). Usando la regla de la cadena para hallar \( z'(t) \), tenemos
\[ \vecs t= \vecs {r}\,{}' (t_0)= \bigl(x'(t_0),\, y'(t_0), \, {f}_x(a,b) x'(t_0) + {f}_y(a,b) y'(t_0)\bigr) \notag\]
que, obviamente, es perpendicular al vector normal al plano tangente \( \vecs n (a,b)=\left( -f_x(a,b), -f_y(a,b), 1 \right) \). En consecuencia, la recta tangente a \( C \) en \( P \) está contenida en el plano tangente.
Derivadas de orden superior. Si \( f \) y \( x=x(t) \), \( y=y(t) \), \( z=z(t) \) pueden derivarse más veces, entonces se puede usar la regla de la cadena para hallar las derivadas de orden superior. Por ejemplo, para dos variables
\[ \begin{align} \psi''&=\dfrac{d}{dt}\left(\dpar{f}x x' + \dpar{f}y y'\right)= \left( \dfrac{\partial^2 f}{\partial x^2} x' + \dfrac{\partial^2 f}{\partial y \partial x}y'\right) x' + \dpar fx x''+ \left(\dfrac{\partial^2 f}{\partial x \partial y} x'+ \dfrac{\partial^2 f}{\partial y^2}y' \right) y'+ \dpar fy y'' \notag\\ &= \dfrac{\partial^2 f}{\partial x^2} {x'}^2 + 2 \dfrac{\partial^2 f}{\partial y \partial x} x' y' +\dfrac{\partial^2 f}{\partial y^2}{y'}^2+ \dpar fx x'' + \dpar fy y''. \notag\end{align} \]
Volveremos sobre esto con más detalle cuando estudiemos, en el siguiente capítulo, la técnica de derivación implícita.
La regla de la cadena para dos variables independientes
Puesto que una derivada parcial no es más que derivar con respecto a una variable manteniendo las demás constantes, la regla de la cadena cuando se cambian más variables se deduce directamente de la que acabamos de ver. Sea \( f(x,y) \) un campo escalar de clase \( C^1 \). Sean \( x=x(u,v) \) e \( y=y(u,v) \) funciones de clase \(C^1 \) con respecto a las nuevas variables \( u \) y \( v \). Entonces la composición \( g(u,v)=f \bigl( x(u,v),y(u,v) \bigr) \) es de clase \( C^1 \) y se verifica
\[ \dpar{g}{u}=\dpar{f}x \dpar{x}u + \dpar{f}y \dpar{y}u \qquad \text{y} \qquad \dpar{g}{v}=\dpar{f}x \dpar{x}v + \dpar{f}y \dpar{y}v \notag\]
Observación sobre la notación. A veces se utiliza la misma letra para denotar la función dependiente, sin tener en cuenta qué variables independientes estamos considerando en cada momento; por eso, a menudo, la regla de la cadena se escribe, usando subíndices, como
\[ f_u =f_x x_u + f_y y_u \qquad \text{y} \qquad f_v = f_x x_v + f_y y_v. \notag\]
Señalemos el doble papel que juega \( f \) en esta expresión como función que depende de \( x \) e \( y \), en primer lugar, y de \( u \) y \( v \) tras el cambio.
Regla de la cadena para coordenadas polares. El cambio a coordenadas polares es, seguramente, el cambio más importante en el plano. Veamos qué nos dice la regla de la cadena cuando pasamos de cartesianas a polares y viceversa. Si \( f(x,y) \) es un campo escalar dado inicialmente en variables cartesianas \((x,y)\) y hacemos el cambio a coordenadas polares \((r,\theta)\), de forma que \( x=r\cos(\theta) \) e \( y=r\sen(\theta) \), entonces, de acuerdo con la regla de la cadena, las derivadas parciales de \( f \) como función de las coordenadas cartesianas \( (x,y) \) están relacionadas con las derivadas parciales de \( f \) como función de las coordenadas polares \( (r,\theta) \) de la siguiente manera:
\[ \begin{align} \dpar{f}{r}&=\dpar{f}x\dpar{x}r+\dpar{f}y\dpar{y}r=\dpar{f}x \cos(\theta) + \dpar{f}y \sen(\theta) =\dpar{f}x \dfrac{x}{\sqrt{x^2+y^2}}+ \dpar{f}y \dfrac{y}{\sqrt{x^2+y^2}}, \notag \\ \dpar{f}{\theta}&=\dpar{f}x\dpar{x}{\theta}+\dpar{f}y\dpar{y}{\theta}=- \dpar{f}x r \sen(\theta) + \dpar{f}y r \cos(\theta)=- y \dpar{f}x + x \dpar{f}y . \notag \end{align} \]
Recíprocamente, si tenemos el campo \( f(r,\theta) \) dado inicialmente en coordenadas polares \(r=\sqrt{x^2+y^2}\) y \( \theta=\arctan(y/x) \), entonces las derivadas parciales de \( f \) como función de las coordenadas cartesianas \( (x,y) \) vienen dadas por
\[ \begin{align} \dpar{f}{x}&=\dpar{f}r\dpar{r}{x}+\dpar{f}{\theta}\dpar{\theta}{x}=\dpar{f}r\dfrac{x}{\sqrt{x^2+y^2}}-\dpar{f}\theta \dfrac{y}{x^2+y^2}= \dpar{f}r \cos(\theta) - \dpar{f}{\theta} \dfrac{\sen(\theta)}r, \notag \\ \dpar{f}{y}&=\dpar{f}r\dpar{r}{y}+\dpar{f}{\theta}\dpar{\theta}{y}= \dpar{f}r\dfrac{y}{\sqrt{x^2+y^2}}+ \dpar{f}\theta\dfrac{x}{x^2+y^2}= \dpar{f}r \sen(\theta) + \dpar{f}{\theta} \dfrac{\cos(\theta)}r. \notag \end{align} \]
Gradiente en coordenadas polares. En la Sección 1.3 hicimos mención a la distinción entre el diferencial y el gradiente de un campo escalar. Si tenemos un campo escalar definido en términos de las coordenadas polares, para calcular su gradiente, el vector de las derivadas parciales con respecto a las variables espaciales, usamos las expresiones que acabamos de calcular, de manera que la expresión del gradiente en coordenadas polares es
\[ \nabla f = \dpar fx {\vecs i} +\dpar fy {\vecs j}= \left( \dpar{f}r \cos(\theta) - \dpar{f}{\theta} \dfrac{\sen(\theta)}r \right) {\vecs i} +\left( \dpar{f}r \sen(\theta) + \dpar{f}{\theta} \dfrac{\cos(\theta)}r \right) {\vecs j}. \notag\]
Veamos un ejemplo simple que puede ayudar a entender la distinción entre diferencial y gradiente. Sea \(f\) el campo expresado en coordenadas cartesianas por \( f(\vecs r)=x^2+y^2 \), entonces \( \nabla f(\vecs r)=2x {\vecs i} + 2y{\vecs j} \). Para el mismo campo \( f \) pero expresado en coordenadas polares \( f(\vecs r)=r^2 \) tenemos \( Df=[f_r,f_\theta]=[2r,0]\), mientras que
\[ \nabla f (\vecs r) = \left( \dpar{f}r \cos(\theta) - \dpar{f}{\theta} \dfrac{\sen(\theta)}r \right) {\vecs i} +\left( \dpar{f}r \sen(\theta) + \dpar{f}{\theta} \dfrac{\cos(\theta)}r \right) {\vecs j} = 2r\cos(\theta) {\vecs i} +2r\sen(\theta){\vecs j}=x {\vecs i} + 2y{\vecs j}. \notag\]
Gradiente de un campo central (2D). Sea \( f \) un campo central de dos variables, de manera que \( f(\vecs r)=\psi(r) \), siendo \( r=\norm{\vecs r} \) el radio polar y \( \psi \) una función de una variable. Entonces, usando la regla de la cadena y teniendo en cuenta que \(\dpar{\psi}{r}=\psi'(r) \) y que \( \dpar{\psi}{\theta}=0 \), se tiene
\[ \nabla f (\vecs r)= \left( \dpar{f}r \cos(\theta) - \dpar{f}{\theta} \dfrac{\sen(\theta)}r \right) {\vecs i} +\left( \dpar{f}r \sen(\theta) + \dpar{f}{\theta} \dfrac{\cos(\theta)}r \right) {\vecs j} = \psi'(r) \cos(\theta) {\vecs i} +\psi'(r) \sen(\theta){\vecs j}= \dfrac{\psi'(r)}{r} \bigl( x {\vecs i}+ y{\vecs j} \bigr)=\dfrac{\psi'(r)}r {\vecs r}.\notag\]
Regla de la cadena para tres variables independientes
Sea \( f(x,y,z) \) un campo escalar de clase \( C^1(U) \). Sean \( x=x(u,v, w) \), \( y=y(u,v,w) \) y \( z=z(u,v,w) \) funciones de clase \( C^1 \) con respecto a tres nuevas variables \( u \), \( v \) y \( w \). Entonces \( g(u,v,w)=f \bigl( x(u,v, w),y(u,v,w), z(u,v,w) \bigr) \) es de clase \(C^1\) y se verifica
\[ \begin{align} \dpar{g}{u}&=\dpar{f}x \dpar{x}u + \dpar{f}y \dpar{y}u + \dpar{f}z \dpar{z}u ,\notag \\ \dpar{g}{v}&=\dpar{f}x \dpar{x}v + \dpar{f}y \dpar{y}v +\dpar{f}z \dpar{z}v , \notag\\ \dpar{g}{w}&=\dpar{f}x \dpar{x}w + \dpar{f}y \dpar{y}w +\dpar{f}z \dpar{z}w. \notag\end{align} \]
Gradiente de un campo central (3D). Si \( f (\vecs r) \) es un campo central de tres variables \( \vecs r=\bigl( x \vecs i + y \vecs j + z \vecs k \bigr)\), entonces \( f \) viene dado por \( f(\vecs r)=\psi(\rho) \), siendo \( \rho(x,y,z)=\norm{(\vecs r)}=\sqrt{x^2+y^2+z^2} \) y \( \psi \) una función de una variable. Entonces, razonando como en el caso bidimensional, su gradiente viene dado por
\[ \nabla f(\vecs r)=\dfrac{\psi'(\rho)}\rho \bigl( x \vecs i + y \vecs j + z \vecs k \bigr)=\dfrac{\psi'(\rho)}\rho \vecs r. \notag\]
En particular, para los campos dados por una potencia de \( \rho \), digamos \( f(\vecs r)=\rho^n \) tenemos \( \nabla (\rho^n)=n\rho^{n-2}\vecs r \) para \( n=0,\pm1,\pm2,\dots \) (excluyendo el origen si \( n\leq 1 \).)
Ejercicios
Ejercicio 1. Comprueba la igualdad de la regla de la cadena para \( f(x,y)=x^2+y^2-xy+1 \) en el punto \( (2,-1) \) al hacer el cambio de variables \( x=2t \) e\( y=-t \).
Ejercicio 2. Comprueba la igualdad de la regla de la cadena para \( f(x,y,z)=x^2+y^2+z^2 \) al hacer el cambio de variables \( x(t)=\cos(t) \), \( y(t)=\sen(t) \),\( z(t)=t \).
Ejercicio 3. Prueba que la ecuación \( y f_x-x f_y=0 \) caracteriza los campos centrales de dos variables. Para ello prueba, aplicando la regla de la cadena, que dicha ecuación se transforma en la ecuación \( f_\theta=0 \) cuando pasamos a coordenadas polares.
Ejercicio 4. Sea \( z=z(x,y) \) un campo escalar de dos variables que verifica \( xz_x+y z_y =0 \). Aplica la regla de la cadena para hallar en qué se transforma esta igualdad cuando pasamos a coordenadas polares.
Ejercicio 5. Sea \( z=z(x,y) \) un campo escalar de dos variables que verifica \( z_x+ z_y =0 \). Si cambiamos las variables independientes \( x \) e \( y \) por las variables \( u=x+y \), \( v=x-y \), ¿qué igualdad verifica \( z \) como función de las nuevas variables \( u \) y \( v \)?
Ejercicio 6. Determina en qué ecuación se transforma la ecuación en derivadas parciales \(\dfrac{\partial^2 z}{\partial y^2}+3\dfrac{\partial^2 z}{\partial x \partial y}+2\dfrac{\partial^2 z}{\partial x^2}=0 \) cuando se aplica el cambio de variables \( u=x-y \), \( v=x-2 y \).
Ejercicio 7. Sea \( y=\psi(x) \) una curva definida para \( x \in \R \), donde \( \psi \) es dos veces derivable y la variable \( t \) representa el tiempo. Entonces la función \( z(x,t)=\psi(x-\omega t) \) representa el desplazamiento de la gráfica de \( \psi \) que se desliza como una onda hacia la derecha del eje \( X \) a velocidad \( \omega \).
- Prueba que \( z(x,t) \) es una solución de la ecuación de ondas \( z_{tt}=\omega ^2z_{xx} \).
- ¿Pasa lo mismo con \( z(x,t)=\psi(x+\omega t) \)?, ¿cómo se interpreta esta función?
Ejercicio 8. Sea \( z(x,t) \) una solución de la ecuación de ondas \( z_{tt}=\omega^2z_{xx} \), donde \( \omega \) es una constante no nula. Aplica el cambio de variables \( u=x-\omega t \), \( v=x+\omega t \) para transformar la ecuación de ondas en la ecuación \( z_{uv}=0 \) y deduce que la solución \( z(x,t) \) puede expresarse como la superposición \(z(x,t)=\psi(x-\omega t ) + \xi (x+\omega t ) \) de dos ondas que viajan, respectivamente, hacia la derecha y hacia la izquierda del eje \(X\) a velocidad \( \omega \).
Ejercicio 9. Escribe las reglas de la cadena para calcular las derivadas parciales de una función de tres variables \( f(x,y,z) \) cuando las tres variables \( x \), \( y \) y \( z \) pasan a depender de dos variables \( u \) y \( v \); digamos \( x=x(u,v) \), \( y=y(u,v) \), \( z=z(u,v) \).
*Ejercicio 10. Sea \( z(x,y) \) un campo escalar de clase \( C^2(\R^2) \). Halla, cuando sea posible, un cambio de variables de la forma \( u=x+ay \), \( v=x+by \) que transforme la ecuación \( \alpha z_{xx}+\beta z_{xy}+\gamma z_{yy}=0 \) (donde \( \alpha, \beta, \gamma \) son constantes, alguna de ellas no nula) en la ecuación \( z_{uv}=0 \).
*Ejercicio 11. En la Sección 1.3 vimos las ecuaciones de Cauchy-Riemann, que ligan las derivadas parciales de dos campos diferenciables \( u(x,y) \), \(v(x,y) \) de la siguiente manera \(u_x=v_y \) y \(u_y=-v_x\). Prueba que si \( f(u,v) \) cumple la ecuación de Laplace \( f_{uu}+f_{vv}=0 \), y hacemos un cambio \( u=u(x,y),v=v(x,y) \) de clase \( C^2 \) que cumplen las ecuaciones de Cauchy-Riemann, entonces \( g(x,y)=f\bigl(u(x,y), v(x,y)\bigr) \) también cumple la ecuación de Laplace para sus variables, es decir, \( g_{xx}+g_{yy}=0 \).

