14.1: Colorear Bordes

Última actualización
Guardar como PDF

Page ID: 114403

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Supongamos que te han dado el trabajo de programar un torneo de tenis round robin con$n$ jugadores. Una forma de abordar el problema es modelarlo como una gráfica: los vértices de la gráfica representarán a los jugadores, y los bordes representarán los partidos que deben jugarse. Al tratarse de un torneo de todos contra todos, cada jugador debe jugar a cualquier otro jugador, por lo que la gráfica estará completa. Crear el horario equivale a asignar un tiempo a cada uno de los bordes, lo que representa el tiempo en el que se va a jugar ese partido.

Observe que hay una restricción. Cuando se ha asignado un tiempo a una ventaja en particular$uv$, ningún otro incidente de borde con ninguno$u$ o$v$ puede asignarse al mismo tiempo, ya que esto significaría que$v$ se supone que cualquiera de los jugadores$u$ o jugadores deben jugar dos juegos a la vez. En lugar de escribir tiempos en cada borde, elegiremos un color para representar cada una de las franjas horarias, y colorearemos los bordes que se van a tocar en ese momento, con ese color.

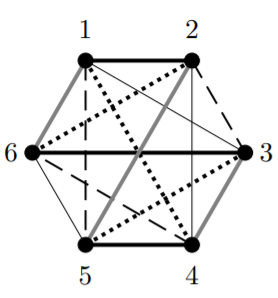
Aquí un ejemplo de un posible horario para el torneo, cuándo$n = 7$.

Ejemplo$\PageIndex{1}$

Los jugadores están numerados desde$1$ el$7$ principio, y extenderemos el torneo a lo largo de siete días. Los juegos para jugar cada día deben tener un color diferente al de los juegos de otros días, pero, debido a que este texto está impreso en blanco y negro, usaremos algunos patrones de líneas, en lugar de colores. Los juegos que se jugarán el lunes se sortearán como de costumbre. Los juegos que se jugarán el martes serán delgados. Los juegos que se jugarán el miércoles estarán salpicados. Los juegos que se jugarán el jueves serán despunteados. Los juegos que se jugarán el viernes serán gruesos. Los juegos que se jugarán el sábado serán grises. Los juegos que se jugarán el domingo serán delgados y discontinuados.

$clipboard_ee0532f90c9afce6ae96e50c8463948be.png$

Esto da un horario. Para cualquiera que tenga problemas para distinguir los “colores” de los bordes, los bordes normales son$12$$37$, y$46$; los bordes delgados son$13$,$24$, y$57$; los bordes punteados son$15$,$26$, y$34$; los bordes punteados son$17$,$36$, y $45$; los bordes gruesos son$23$$47$, y$56$; los bordes grises son$14$,$25$, y$67$; y los bordes punteados delgados son$16$,$27$, y$35$.

Definición: Proper$k$-Edge-Colouring

Una $k$coloración adecuada de bordes de una gráfica$G$ es una función que asigna a cada borde de$G$ uno de los$k$ colores, de tal manera que a los bordes que se encuentran en un vértice final se les deben asignar diferentes colores.

La restricción de que los bordes del mismo color no pueden encontrar en un vértice resulta ser una restricción útil en varios contextos.

Si el gráfico es lo suficientemente grande, es probable que se queden sin colores que puedan distinguirse fácilmente (y nos cansamos de escribir los nombres de los colores). La convención habitual es referirse a cada color por un número (el primer color es color$1$, etc.) y etiquetar los bordes con los números en lugar de usar colores.

Definición:$k$-Edge-Colourable

Una gráfica$G$ es $k$coloreable en los bordes si admite una$k$ coloración adecuada de bordes. El entero más pequeño$k$ para el que$G$ es$k$ -borde-coloreable se llama el número cromático del borde, o índice cromático de$G$.

Notación

El índice cromático de$G$ se denota por$χ'(G)$, o simplemente por$χ'$ si el contexto es inequívoco.

Aquí hay una observación fácil:

Proposición$\PageIndex{1}$

Para cualquier gráfica$G$,$χ'(G) ≥ ∆(G)$.

Prueba: Recordemos que$∆(G)$ denota el valor máximo de$d(v)$ sobre todos los vértices$v$ de$G$. Entonces hay algún vértice$v$ de$G$ tal que$d(v) = ∆(G)$. En cualquier coloración adecuada de los bordes, los$d(v)$ bordes con los que inciden$v$, deben asignarse diferentes colores. Por lo tanto, cualquier coloración adecuada de bordes debe tener al menos colores$d(v) = ∆(G)$ distintos. Esto significa$χ'(G) ≥ ∆(G)$.

Ejemplo$\PageIndex{2}$

El color que se da en el Ejemplo 14.1.1 muestra que$χ'(K_7) ≤ 7$, ya que pudimos colorear correctamente los bordes$K_7$ usando siete colores.

Para demostrar que no podemos colorear$K_7$ con menos de$7$ colores, observe que debido a que cada uno de$7$ los vértices solo puede ser incidente con un borde de un color dado, no puede haber más que$3$ bordes coloreados con un color dado ($3$los bordes ya están incidentes con $6$de los$7$ vértices, y un cuarto borde tendría que ser incidente con otros dos).

Sabemos que$K_7$ tiene$\binom{7}{2} = 21$ bordes, por lo que si en la mayoría de$3$ los bordes se pueden colorear con cualquier color dado, requeriremos al menos$7$ colores para el color de los bordes correctamente$K_7$. Así$χ'(K_7) ≥ 7$.

Así, lo hemos demostrado$χ'(K_7) = 7$.

Esto demuestra que$χ'(K_7) = 7 > ∆(K_7) = 6$, por lo que no siempre es posible lograr la igualdad en el encuadernado dado por la Proposición 14.1.1. Nuestro siguiente ejemplo muestra que a veces es posible lograr la igualdad en ese límite

Ejemplo$\PageIndex{3}$

Aquí hay una$5$ coloración adecuada de bordes de$K_6$:

$clipboard_e7df9f6851da988bf2d73b5d6e7c1c905.png$

En caso de que los colores de los bordes sean difíciles de distinguir, los bordes gruesos son$12$$36$, y$45$; los bordes delgados son$13$$24$, y$56$; los bordes punteados son$14$$26$, y$35$; los bordes punteados son$15$,$23$, y$46$; y; y los bordes grises son$16$,$25$, y$34$. Esto demuestra que$χ'(K_6) ≤ 5$. Dado que la valencia de cada vértice de$K_6$ es$5$, la Proposición 14.1.1 implica que$χ'(K_6) ≥ 5$. Armando estos, vemos que$χ'(K_6) = ∆(K_6) = 5$, así se logra la igualdad en el encuadernado de la Proposición 14.1.1 mediante$K_6$.

El siguiente resultado bastante notable fue probado por Vadim Vizing en$1964$:

Teorema$\PageIndex{1}$: Vizing's Theorem

Para cualquier gráfica simple$G$,$χ'(G) ∈ \{∆(G), ∆(G) + 1\}$.

Prueba: No vamos a repasar la prueba de este teorema.

Definición: Gráfica Clase Uno y Gráfica Clase Dos

Si$χ'(G) = ∆(G)$ entonces$G$ se dice que es una gráfica de clase uno, y si$χ'(G) = ∆(G) + 1$ entonces$G$ se dice que es una gráfica de clase dos.

A la fecha, las gráficas no se han clasificado completamente según qué gráficas son de clase uno y cuáles son de clase dos, pero se ha comprobado que “casi todas” gráficas son de clase uno. Técnicamente, esto significa que si eliges una gráfica aleatoria de todas las gráficas en la mayoría de los$n$ vértices, la probabilidad de que elijas una gráfica de clase dos se acerca a$0$ medida que se$n$ acerca al infinito.

Hay, sin embargo, infinitamente muchas gráficas de clase dos; el mismo argumento que usamos para mostrar que también se$χ'(K_7) ≥ 7$ puede usar para probar que$χ'(K_{2n+1}) = 2n + 1$ para cualquier entero positivo$n$, ya que el número de aristas es

\[\dfrac{(2n + 1)(2n)}{2} = n(2n + 1)\]

y cada color solo se puede usar para$n$ colorear los bordes. Ya que$∆(K_{2n+1}) = 2n$, esto demuestra que$K_{2n+1}$ es la clase dos.

Se ha demostrado que las familias numerosas de gráficas son gráficas de clase uno. Dedicaremos la mayor parte del resto de esta sección a probar que todas las gráficas de una familia en particular son de clase uno. Primero, necesitamos definir a la familia.

Definición: Bipartition

Una gráfica es bipartita si sus vértices se pueden dividir en dos conjuntos$V_1$ y$V_2$, de tal manera que cada borde de la gráfica tiene uno de sus extremos en$V_1$, y el otro en$V_2$. Los conjuntos$V_1$ y$V_2$ forman una bipartición de la gráfica.

Ejemplo$\PageIndex{4}$

Las siguientes gráficas son bipartitas. Cada borde tiene un vértice final en el lado izquierdo y uno en el derecho.

$clipboard_eca41666a38f5f53127d751b5c6b3ace8.png$

La gráfica no$K_n$ es bipartita si$n ≥ 3$. El primer vértice también puede entrar$V_1$; el segundo vértice es adyacente a él, por lo que debe entrar$V_2$; pero el tercer vértice es adyacente a ambos, por lo que no puede entrar en ninguno$V_1$ o$V_2$.

Si bien en este capítulo no se utilizará la siguiente clase de gráficas bipartitas, son una clase importante de gráficas bipartitas que volverán a aparecer más adelante.

Definición: Gráfica Bipartita Completa

La gráfica bipartita completa,$K_{m,n}$, es la gráfica bipartita sobre$m + n$ vértices con tantos bordes como sea posible sujeto a la restricción de que tiene una bipartición en conjuntos de cardinalidad$m$ y$n$. Es decir, tiene todos los bordes entre los dos conjuntos de la bipartición.

Antes de probar que todas las gráficas bipartitas son de clase uno, necesitamos entender un poco mejor la estructura de las gráficas bipartitas. Aquí hay un teorema importante.

Teorema$\PageIndex{2}$

Una gráfica$G$ es bipartita si y sólo si no$G$ contiene ningún ciclo de longitud impar.

Prueba

Esta es una declaración si y sólo si, entonces tenemos dos implicaciones que probar.

$(⇒)$Demostramos lo contrapositivo, que si$G$ contiene un ciclo de longitud impar, entonces$G$ no puede ser bipartito.

Let

\[(v_1, v_2, . . . , v_{2k+1}, v_1)\]

ser un ciclo de longitud impar en$G$. Intentamos establecer una bipartición$V_1$ y$V_2$ para$G$. Sin pérdida de generalidad, podemos suponer eso$v_1 ∈ V_1$. Entonces debemos tener$v_2 ∈ V_2$ desde entonces$v_2 ∼ v_1$. Continuando de esta manera alrededor del ciclo, vemos que para cada$1 ≤ i ≤ k$, tenemos$v_{2i+1} ∈ V_1$ y$v_{2i} ∈ V_2$. En particular,$v_{2k+1} ∈ V_1$, pero$v_1 ∈ V_1$ y$v_1 ∼ v_{2k+1}$, contradiciendo el hecho de que cada borde debe tener uno de sus endvertices adentro$V_2$. Así, no$G$ es bipartita.

$(⇐)$Déjese$G$ ser una gráfica que no sea bipartita. Debemos demostrar que hay un ciclo impar en$G$.

Si cada componente conectado de$G$ es bipartito, entonces$G$ es bipartito (elija un conjunto de la bipartición de cada componente conectado; deje$V_1$ ser la unión de estos, y$V_2$ el conjunto de todos los demás vértices de$G$; esta es una bipartición para$G$). Por lo tanto hay al menos un componente conectado de$G$ que no es bipartito.

Elija cualquier vértice$u$ de un componente conectado no bipartito de$G$, y asígnelo a$V_1$. Coloca a todos sus vecinos en$V_2$. Coloca a todos sus vecinos en$V_1$. Repita este proceso, en cada paso poniendo todos los vecinos de cada vértice de$V_1$$V_2$, y luego todos los vecinos de cada vértice de$V_2$ en$V_1$.

Como este componente no es bipartito, en algún momento debemos encontrarnos con la situación en la que colocamos un vértice$v$$V_j$, pero un vecino$u_1$ de también$v$ está en$V_j$ (para algunos$j ∈ \{1, 2\}$). Por nuestra construcción de$V_1$ y$V_2$, debe haber un paseo de$u_1$ a$v$ que alterna entre vértices en$V_j$ y vértices en$V_{3−j}$. Por la Proposición 12.3.1, de hecho debe haber un camino de$u_1$ a$v$ que alterna entre los vértices en$V_j$ y los vértices en$V_{3−j}$. Dado que el camino alterna entre los dos conjuntos pero comienza y termina en$V_j$, tiene una longitud par. Por lo tanto,$u_1$ sumar al final de esta ruta se obtiene un ciclo de longitud impar en G.

Para demostrar que las gráficas bipartitas son de clase uno, requerimos de un lema.

Lema$\PageIndex{1}$

Dejar$G$ ser una gráfica conectada que no sea un ciclo de longitud impar. Luego,$G$ los bordes de$G$ pueden ser$2$ coloreados para que los bordes de ambos colores incidan con cada vértice que no sea de hoja. (Nota: esto probablemente no será una$2$ coloración adecuada de bordes de$G$.)

Prueba

Primero consideramos el caso donde cada vértice de$G$ tiene valencia uniforme.

Elija un vértice$v$ de$G$ sujeto a la restricción que si algún vértice de$G$ tiene valencia mayor que$2$, entonces$v$ es tal vértice. Dado que cada vértice de$G$ tiene valencia par, podemos encontrar un recorrido de Euler$G$ que comienza y termina en$v$. Colores de borde alternos alrededor de este recorrido. Claramente, cada vértice que se visita en medio del recorrido (es decir, cada vértice excepto posiblemente$v$) debe ser incidente con bordes de ambos colores, ya que cualquiera que sea el color que se le dé al borde que viajemos para llegar a ese vértice, el otro color se le dará al borde que viajemos al salir de ese vértice . Si algún vértice de$G$ tiene valencia mayor que$2$, entonces por nuestra elección de$v$, la valencia de$v$ debe ser mayor que$2$, así$v$ se visita en medio del recorrido, y esta coloración tiene la propiedad deseada. Si cada vértice de$G$ tiene valencia$2$, entonces ya que$G$ está conectado,$G$ debe ser un ciclo (ver Ejercicio 12.3.1 (4). Dado que no$G$ es un ciclo de longitud impar (por hipótesis),$G$ debe ser un ciclo de longitud par. Por lo tanto el número de aristas de$G$ es par, por lo que el recorrido comenzará y terminará con bordes de colores opuestos, ambos incidentes con$v$. Nuevamente vemos que este colorante tiene la propiedad deseada.

Supongamos ahora que$G$ tiene al menos un vértice de valencia impar.

Crea un nuevo vértice,$u$, y agrega bordes entre$u$ y cada vértice$G$ que tenga valencia impar. Todos los vértices de$G$ tendrán incluso valencia en esta nueva gráfica, y por el corolario al lema de apretón de manos de Euler, también$u$ deben tener valencia par, por lo que esta gráfica tiene un recorrido por Euler; de hecho, podemos encontrar una gira de Euler que comienza con el vértice$u$. Colores de borde alternos alrededor de este recorrido. Eliminar$u$ (y sus bordes incidentes) pero conservar los colores en el borde de$G$. Afirmamos que este colorante tendrá la propiedad deseada. Si un vértice$v$ tiene valencia uniforme$G$, debe visitarse en medio del recorrido y los bordes en los que viajemos para llegar$v$ y salir$v$ tendrán diferentes colores. Ninguno de estos bordes es incidente con$u$, así que ambos están adentro$G$. Si un vértice$v$ tiene valencia$1$ adentro$G$, entonces$v$ es una hoja y el color de su borde incidente no importa. Si un vértice$v$ tiene valencia impar al menos$3$ en$G$, entonces$v$ se visita al menos dos veces en medio del recorrido. Solo una de estas visitas puede involucrar el borde$uv$, por lo que durante cualquier otra visita, los bordes en los que viajemos para llegar$v$ y para salir$v$ tendrán diferentes colores. Ninguno de estos bordes es incidente con$u$, así que ambos están adentro$G$. Así, esta coloración tiene la propiedad deseada.

Notación

Dada una coloración de bordes (no necesariamente adecuada)$\mathcal{C}$, usamos$c(v)$ para denotar el número de colores distintos que se han utilizado en los bordes con los que inciden$v$. Claramente,$c(v) ≤ d(v)$.

Definición: Mejora y Óptima

Una coloración de bordes$\mathcal{C}'$ es una mejora en una coloración de bordes$\mathcal{C}$ si usa los mismos colores que$\mathcal{C}$, pero$\sum_{v∈V} c'(v) > \sum_{v∈V} c(v)$.

Una coloración de bordes es óptima si no es posible mejorar.

Observe que ya que$c(v) ≤ d(v)$ para cada$v ∈ V$, si

\[\sum_{v∈V}c(v) = \sum_{v∈V}d(v) \]

entonces debemos tener$c(v) = d(v)$ para cada$v ∈ V$. Esto equivale precisamente a la definición de una coloración adecuada.

Por fin, estamos listos para demostrar que las gráficas bipartitas son de clase uno.

Teorema$\PageIndex{3}$

Si$G$ es bipartito, entonces$χ'(G) = ∆(G)$.

Prueba

Que$G$ sea una gráfica bipartita. Hacia una contradicción, supongamos que$χ'(G) > ∆(G)$.

Deja$\mathcal{C}$ ser una óptima$∆(G)$ coloración de bordes de$G$. Por supuesto, no$\mathcal{C}$ habrá una coloración de borde adecuada, por lo que debe haber algún vértice$u$ tal que$c(u) < d(u)$. Según el Principio de Pigeonhole, se$j$ debe usar algún color para colorear al menos dos de los bordes incidentes con$u$, y dado que hay$∆(G) ≥ d(u)$ colores en total y solo se$c(u)$ usan en bordes incidentes con$u$, debe haber algún color$i$ que no se use para colorear cualquier incidente de borde con$u$.

Considera solo los bordes de los$G$ que han sido coloreados con cualquiera$i$ o$j$ en la coloración$\mathcal{C}$. Dado que$G$ es bipartito, estos bordes no pueden incluir un ciclo impar. Aplicamos Lema 14.1.1 a cada componente conectado formado por estos bordes para volver a colorear estos bordes. Nuestra recoloración utilizará solo colores$i$ y$j$, y si un vértice$v$ fue incidente en al menos dos bordes coloreados con uno$i$ o$j$ adentro$\mathcal{C}$, entonces debajo de la coloración,$v$ será incidente con al menos un borde coloreado con$i$ y en al menos un borde coloreado con$j$. Deja en paz a todos los demás colores de borde, y llama a este nuevo color$\mathcal{C}'$.

Afirmamos que$\mathcal{C}'$ es una mejora sobre$\mathcal{C}$. Cualquier vértice$v$ que tuviera como máximo un borde incidente coloreado con cualquiera$i$ o$j$ debajo$\mathcal{C}$, seguirá teniendo exactamente los mismos colores excepto que el borde coloreado$i$ o$j$ podría haber cambiado su color al otro de$i$ y$j$. En todo caso, tendremos$c'(v) = c(v)$. Cualquier vértice$v$ que tuviera al menos dos bordes incidentes coloreados con cualquiera$i$ o por$j$ debajo$\mathcal{C}$, seguirá teniendo todos los mismos colores excepto que ahora tendrá bordes incidentes coloreados con ambos$i$ y$j$, así$c'(v) ≥ c(v)$. Además, tenemos$c'(u) > c(u)$ desde los bordes incidentes con$u$ ahora incluir bordes coloreados con ambos$i$ y$j$, donde antes solo había bordes coloreados con$j$. Por lo tanto,

\[\sum_{v∈V}c'(v) = \sum_{v∈V}c(v) \]

así$\mathcal{C}'$ es una mejora sobre$\mathcal{C}$, como se afirma.

Hemos contradicho nuestra suposición de que$\mathcal{C}$ es una$∆(G)$ coloración óptima de bordes. Esta contradicción sirve para demostrarlo$χ'(G) = ∆(G)$.

Ejercicio$\PageIndex{1}$

1) Demostrar que cada árbol es una gráfica de clase uno.

2) Demostrar que cada ciclo de longitud impar es una gráfica de clase dos.

3) Encuentra una gráfica que contenga un ciclo de longitud impar, pero que sea una gráfica de clase uno.

4) Para cada una de las siguientes gráficas, busque el número cromático de borde, determine si la gráfica es de clase uno o clase dos, y encuentre una coloración de bordes adecuada que utilice el menor número posible de colores.

a) Las dos gráficas en el Ejercicio 13.2.1 (2).

b) Las dos gráficas del Ejemplo 14.1.4.

c) El esqueleto de un dodecaedro (el más a la izquierda de las dos gráficas dibujadas a continuación).

d) La gráfica Petersen (la más a la derecha de las dos gráficas dibujadas a continuación). Se puede suponer, sin pruebas, que la gráfica Petersen es de clase dos.

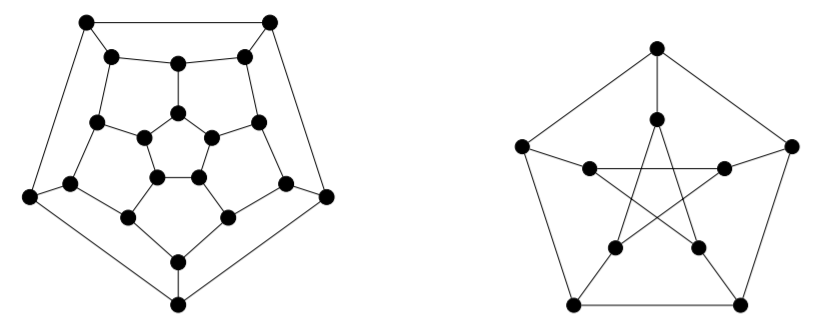
$clipboard_eb752656a119a2a9e23e5699821a945b8.png$

5) Encontrar un enfoque sistemático para colorear los bordes de las gráficas completas que lo demuestre$χ'(K_{2n−1}) = χ'(K_{2n}) = 2n − 1$.

6) Encontrar un enfoque sistemático para colorear los bordes de gráficas bipartitas completas que lo demuestre$χ'(K_{m,n}) = ∆(K_{m,n}) = \max\{m, n\}$.

Ejercicio$\PageIndex{2}$

Los siguientes ejercicios ilustran algunas de las conexiones entre los ciclos de Hamilton y la coloración de bordes.

1) Definición. Se dice que una gráfica está conectada a Hamilton si hay una ruta de Hamilton desde cada vértice en la gráfica hasta cada uno de los otros vértices de la gráfica. Demostrar que si$G$ es bipartita y tiene al menos$3$ vértices, entonces no$G$ es Hamiltonconnected.

[Pista: Demuéstralo por contradicción. Considera la longitud de un camino Hamilton y dónde puede terminar.]

2) Supongamos que$G$ es una gráfica bipartita con$V_1$ y$V_2$ formando una bipartición. Demuestre que si$|V1| \neq |V2|$ entonces no$G$ tiene ciclo Hamilton.

3) Demostrar que si cada vértice de$G$ tiene valencia$3$, y$G$ tiene un ciclo Hamilton, entonces$G$ es clase uno.

[Pista: Usa el corolario del lema de apretón de manos de Euler y encuentra la manera de asignar colores a los bordes del ciclo Hamilton.]

Search

Text Color

Text Size

Margin Size

Font Type