15.1: Gráficas Planas

Última actualización
Guardar como PDF

Page ID: 114436

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Visualmente, siempre existe el riesgo de confusión cuando se dibuja una gráfica de tal manera que algunos de sus bordes se cruzan entre sí. Además, en las realizaciones físicas de una red, dicha configuración puede generar costos adicionales (piense en construir un paso elevado en comparación con construir una intersección). Por lo tanto, es útil poder determinar si una gráfica en particular se puede dibujar o no de tal manera que no se crucen bordes.

Definición: Planar

Una gráfica es plana si se puede dibujar en el plano ($\mathbb{R}^2$) para que las aristas que no compartan un vértice final no tengan puntos en común, y las aristas que sí comparten un vértice final no tengan otros puntos en común.

Tal dibujo se llama incrustación plana de la gráfica.

Ejemplo$\PageIndex{1}$

La siguiente gráfica es plana:

$clipboard_ee35dbbc6149d29294c1838b61395a736.png$

Aquí hay una incrustación plana:

$clipboard_eb1f86e89098da2f2999b5a0db64fb097.png$

Teorema$\PageIndex{1}$

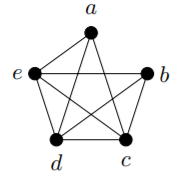
La gráfica no$K_5$ es plana.

Prueba

Etiquetar los vértices de$K_5$ as$v_1, . . . , v_5$. Considera el$3$ -ciclo$(v_1, v_2, v_3, v_1)$. El vértice$v_4$ debe estar dentro o fuera del límite determinado por este$3$ ciclo. Además, dado que hay un borde entre$v_4$ y$v_5$, el vértice$v_5$ debe estar en el mismo lado (interior o exterior) que$v_4$.

Supongamos primero eso$v_4$ y$v_5$ se encuentran dentro del límite. Los bordes$v_1v_4$,$v_2v_4$, y$v_3v_4$ dividen el área dentro del límite en tres regiones, y$v_5$ deben estar dentro de una de estas tres regiones. Uno de$v_1$,$v_2$, y no$v_3$ es un rincón de esta región, y de hecho se encuentra fuera de ella mientras$v_5$ yace dentro de ella, haciendo imposible dibujar el borde de este vértice a$v_5$.

La prueba es similar si$v_4$$v_5$ yace en el exterior del límite determinado por el$3$ ciclo$(v_1, v_2, v_3, v_1)$.

Teorema$\PageIndex{2}$

La gráfica bipartita completa no$K_{3,3}$ es plana.

Prueba

Etiquetar los vértices en uno de los conjuntos de biparticiones como$v_1$$v_2$,$v_3$,, y los vértices de la otra parte como$u_1$,$u_2$,$u_3$. Considera el$4$ ciclo

\[(v_1, u_1, v_2, u_2, v_1).\]

El vértice$v_3$ debe estar dentro o fuera del límite determinado por este$4$ ciclo. Además, dado que hay un borde entre$v_3$ y$u_3$, el vértice$u_3$ debe estar en el mismo lado (interior o exterior) que$v_3$.

Supongamos primero eso$v_3$ y$u_3$ se encuentran dentro del límite. Los bordes$v_3u_1$ y$v_3u_2$ dividir el área dentro del límite en dos regiones, y$u_3$ deben estar dentro de una de estas dos regiones. Uno de$v_1$ y$v_2$ no se encuentra en el límite de esta región, y de hecho se encuentra fuera de ella mientras$u_3$ se encuentra dentro de ella, haciendo imposible dibujar el borde de este vértice a$u_3$.

La prueba es similar si$v_3$$u_3$ yace en el exterior del límite determinado por el$4$ ciclo$(v_1, u_1, v_2, u_2, v_1)$.

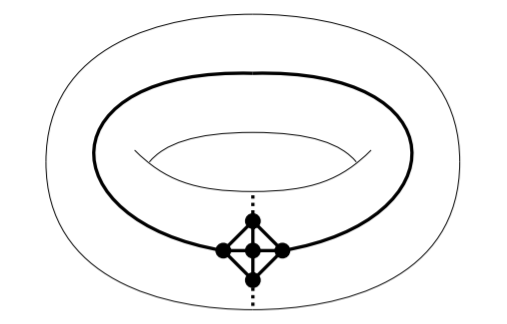
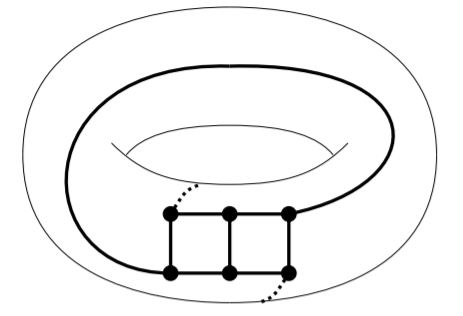
Sin embargo, ambos$K_5$ y se$K_{3,3}$ pueden incrustar en la superficie de lo que llamamos un toro (una forma de rosquilla), sin bordes que se encuentran excepto en vértices extremos mutuos. Las incrustaciones se muestran en las Figuras 15.1.1 y 15.1.2.

Figura$\PageIndex{1}$:$K_5$ incrustado en un toro. El borde punteado se envuelve a través del agujero en el toro. (Copyright; autor vía fuente)

Se podría pensar en este punto que cada gráfica se puede incrustar en el toro sin que los bordes se reúnan excepto en los vértices finales mutuos, pero este no es el caso. De hecho, para cualquier superficie hay gráficas que no se pueden incrustar en esa superficie (sin que ningún borde se encuentre excepto en vértices extremos mutuos).

Para cualquier incrustación de una gráfica plana, hay otra gráfica plana incrustada que está estrechamente relacionada con ella, que ahora describiremos. Observe que una incrustación plana divide el plano en regiones.

Definición: Caras

Las regiones en las que una incrustación plana divide el plano, se denominan las caras de la incrustación plana.

Figura$\PageIndex{2}$:$K_{3,3}$ incrustado en un toro. El borde punteado se envuelve a través del agujero en el toro. (Copyright; autor vía fuente)

Ejemplo$\PageIndex{2}$

En estos dibujos, hemos etiquetado las caras de las dos incrustaciones planas con$f_1$,$f_2$, etc., para mostrarlas claramente.

$clipboard_e17286eae7b594c41ee60e3bd50ab8c6d.png$

Notación

Usamos$F(G)$ (o simplemente$F$ si la gráfica es clara desde el contexto) para denotar el conjunto de caras de una incrustación plana.

Definición: Dual Graph

Decimos que un borde es incidente con una cara de una incrustación plana, si se encuentra en el límite de la cara (o dentro de la cara). Para una incrustación plana de$G$, la gráfica dual o planar dual,$G^∗$, se define por$V (G^∗) = F(G)$, y$f_i ∼ f_j$ si y sólo si hay un borde de$G$ eso es incidente con ambos$f_i$ y$f_j$.

Es posible que la gráfica dual de una incrustación plana no sea una gráfica simple, aunque la gráfica original fuera simple.

Ejemplo$\PageIndex{3}$

Aquí mostramos cómo encontrar los duales planos de las incrustaciones dadas en el Ejemplo 15.1.2. Incluimos la incrustación original como arriba; los vértices grises y los bordes discontinuas son los vértices y bordes de la gráfica dual.

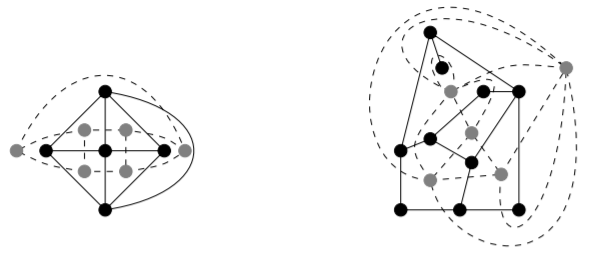
$clipboard_ef7580fe41a12eac776e1f851e0fa969b.png$

Tenga en cuenta que la segunda gráfica tiene bucles y multibordes. Tenga en cuenta también que aunque$f_1$ y se$f_5$ encuentran en un vértice en la incrustación de la primera gráfica, no son adyacentes en el dual ya que no comparten un borde común.

Algunas otras observaciones útiles:

$|E(G)| = |E(G^∗)|$, y cada borde punteado cruza exactamente un borde negro;

la valencia del vértice$f_i$ adentro$G^∗$ es igual al número de bordes que traces, si trazas alrededor del perímetro de la cara$f_i$ en$G$ (así los bordes que colgan dentro de la cara se cuentan dos veces).

Proposición$\PageIndex{1}$

La gráfica dual de una incrustación plana tiene una incrustación plana natural, por lo que es una gráfica plana. Además,$(G^∗)^∗ = G$.

Prueba: Ambos hechos se derivan de manera bastante directa de las definiciones.

Ejemplo$\PageIndex{4}$

¡Ten cuidado! — Dos incrustaciones planas diferentes de la misma gráfica pueden tener gráficas duales no isomórficas, como mostramos aquí.

$clipboard_ee93df4a50bfa25957a16a050204b7174.png$

En el dual planar de la incrustación a la izquierda,$f_1$ tendrá valencia$3$;$f_2$ y$f_3$ tendrá valencia$4$; y$f4$ tendrá valencia$7$. En el dual planar de la incrustación a la derecha,$f_1$ tendrá valencia$3$;$f_2$ tendrá valencia$5$;$f_4$ tendrá valencia, tendrá valencia$4$, y$f_3$ tendrá valencia$6$. Dado que las listas$3$$4$,$4$,,$7$ y$3$$4$,$5$,, no$6$ son permutaciones entre sí, los duales planos no pueden ser isomórficos.

Antes de pasar a otros temas relacionados, presentamos una clasificación de gráficos planos. Este es un teorema de Kuratowski (de cuyo nombre se toma la notación para gráficas completas). Demostró este resultado en$1930$.

Necesitamos una nueva definición.

Definición: Subdivisión

Un borde se$uv$ puede subdividir colocando un vértice en algún lugar a lo largo de su longitud. Técnicamente, esto significa eliminar$uv$, agregar un nuevo vértice$x$, y agregar los bordes$ux$ y$vx$.

Una subdivisión de una gráfica es una gráfica que se obtiene subdividiendo algunos de los bordes de la gráfica.

Ejemplo$\PageIndex{5}$

Un ejemplo se muestra en la Figura 15.1.3. Los vértices blancos son los nuevos.

Figura$\PageIndex{3}$: Una subdivisión de$K_5$. (Copyright; autor vía fuente)

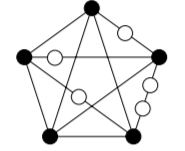
Teorema$\PageIndex{3}$: Kuratowski's Theorem

Una gráfica$G$ es plana si y sólo si ninguna subgráfica de$G$ es una subdivisión de$K_5$ o$K_{3,3}$.

Prueba

Una dirección de la prueba es bastante sencilla, ya que ya lo hemos probado$K_5$ y no$K_{3,3}$ somos planos. Sin embargo, no intentaremos probar este teorema en este curso.

Una subdivisión de$K_5$ o de a veces$K_{3,3}$ será muy difícil de encontrar, pero sí existen algoritmos eficientes. Normalmente, para demostrar que una gráfica es plana se encuentra una incrustación plana.

Para probar que una gráfica no es plana, encontrarías una subgráfica que sea una subdivisión de cualquiera$K_5$ o$K_{3,3}$.

Ejemplo$\PageIndex{6}$

Encuentra una subgráfica que sea una subdivisión de$K_5$ o$K_{3,3}$ en esta gráfica, para mostrar que no es plana.

$clipboard_e2f6c39dbb180daf4f6a28fa10b8cfe3b.png$

Solución

Aquí hay una subdivisión de$K_{3,3}$ en la gráfica dada. Los vértices blancos son los vértices que están subdividiendo los bordes. Se han eliminado bordes innecesarios. La bipartición consiste en$\{a, c, e\}$ y$\{b, g, h\}$.

$clipboard_eb1637e8a5bba583b36b125717d19413e.png$

Ejercicio$\PageIndex{1}$

1) Demostrar que si una gráfica$G$ tiene una subgráfica$H$ que no es plana, entonces no$G$ es plana. Deducir que para cada$n ≥ 6$, no$K_n$ es planar.

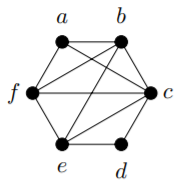
2) Encuentra una incrustación plana de la siguiente gráfica y encuentra la gráfica dual de tu incrustación:

$clipboard_e329d94bc706b93de1407fa20cc27a051.png$

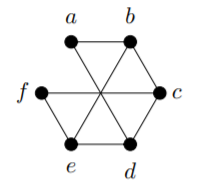
3) Encuentra una incrustación plana de la siguiente gráfica y encuentra la gráfica dual de tu incrustación:

$clipboard_e889c6e5539e06f52687f208c38faebcf.png$

4) La gráfica del Ejemplo 15.1.6 también tiene una subgrafía que es una subdivisión de$K_5$. Encuentra tal subgrafo.

5) Demostrar que la gráfica Petersen no es plana. [Pista: Usa el teorema de Kuratowski.]

6) Encuentre incrustaciones planas de las dos gráficas que se muestran a continuación. (Estas gráficas se obtienen eliminando una arista$K_5$ y borrando una arista de$K_{3,3}$, respectivamente).

$clipboard_edb8cbc35badbd08318881a5eb650b72f.png$

Search

Text Color

Text Size

Margin Size

Font Type