16.2: Cuadrados latinos mutuamente ortogonales (MOLS)

Última actualización
Guardar como PDF

Page ID: 114334

Joy Morris
University of Lethbridge

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La mayor parte de la teoría del diseño se ocupa de crear estructuras agradables en las que diferentes combinaciones de elementos ocurren con igual frecuencia. Esta es la estructura general de toda la teoría del diseño que vamos a cubrir aquí, y en este contexto, los cuadrados latinos ortogonales son lo natural de aprender.

Definición: Ortogonal

Dos cuadrados latinos$S_1$ y$S_2$ son ortogonales si cuando miramos cada posición en turno y consideramos el par ordenado formado por la entrada de$S_1$ en esa posición, y la entrada de$S_2$ en esa posición, aparece cada par ordenado posible.

Entonces aquí, estamos mirando posiciones en la estructura de los cuadrados latinos, y tratando de asegurar que cada par ordenado aparezca en cada posición. Observe que dado que el conjunto$N$ tiene$n$ elementos, el número total de pares ordenados posibles es$n^2$ (hay$n$ opciones para la primera entrada y$n$ opciones para la segunda entrada). Un cuadrado latino tiene$n^2$ posiciones ya que tiene$n$ filas y$n$ columnas. Así, si cada par ordenado posible aparece en cada posición, entonces cada par ordenado debe aparecer exactamente una vez.

Una vez más, Euler estuvo involucrado en los orígenes de este problema. De hecho, el nombre cuadrado latino proviene de su terminología. En$1782$, planteó el problema de ordenar a$36$ los oficiales en una$6 \times 6$ plaza. Los oficiales provienen de$6$ diferentes regimientos (que denotó con los caracteres latinos$a$,$b$,$c$,$d$$e$, y$f$) y cada uno ocupa uno de los$6$ posibles rangos (que denotó con los caracteres griegos$α$,$β$, $γ$,$δ$,$ε$, y$ζ$). No hay dos oficiales del mismo regimiento que tengan el mismo rango. La pregunta que planteó fue: ¿es posible organizar a los oficiales en la plaza para que en cada fila y en cada columna, haya precisamente un oficial de cada regimiento, y precisamente un oficial de cada rango? Como estaba usando letras griegas y romanas para denotar las clases, llamó a esto un “cuadrado greco-latino”. Eligió el primer paso para que consistiera en disponer los regimientos, es decir, que cada regimiento reservara 6 puestos en la plaza para ser llenados con oficiales de ese regimiento. Posteriormente, trataría de asignar filas a los oficiales en estos$6$ cargos. Dado que los regimientos fueron denotados por caracteres latinos, llamó a este primer paso un “cuadrado latino”. El cuadrado greco-latino de su pregunta es un par de cuadrados ortogonales latinos de orden$6$, ya que hay que haber un oficial de cada regimiento que ostente cada una de las filas posibles.

Euler no pudo encontrar una solución a este problema. Como tampoco hay par de cuadrados latinos ortogonales de orden$2$ (y posiblemente por otras razones), conjetura que no hay par de cuadrados latinos ortogonales de orden$n$ para ningún$n ≡ 2$ (mod$4$). Si bien Euler tenía razón de que no hay par de cuadrados ortogonales latinos de orden$6$, su conjetura no era cierta. En$1959$ —$1960$, Bose, Shrikhande, y Parker primero encontraron construcciones para pares de cuadrados latinos ortogonales de órdenes$22$ y$10$, y luego encontraron una construcción general que puede producir un par de cuadrados latinos ortogonales de orden$n$ para cada$n > 6$ con$n ≡ 2$ ( mod$4$).

Ejemplo$\PageIndex{1}$

Aquí hay un par de cuadrados ortogonales latinos de orden$3$:

\[ 1 \; \; 2 \; \; 3 \;\;\;\;\;\;\;\;\;\;\;\; 1\;\;2\;\;3 \\ 3 \; \; 1 \; \; 2 \;\;\;\;\;\;\;\;\;\;\;\; 2\;\;3\;\;1 \\ 2 \; \; 3 \; \; 1 \;\;\;\;\;\;\;\;\;\;\;\; 3\;\;1\;\;2 \]

Vemos que los pares ordenados$(1, 1)$,$(2, 2)$, y$(3, 3)$ aparecen en la primera fila; los pares$(3, 2)$,$(1, 3)$, y$(2, 1)$ aparecen en la segunda fila; y los pares$(2, 3)$,$(3, 1)$, y$(1, 2)$ aparecen en la tercera fila. Cada par ordenado posible cuyas entradas se encuentran en$\{1, 2, 3\}$ ha aparecido.

Hay un bonito patrón a los cuadrados dados en este ejemplo. El primero sigue la construcción general que mencionamos al inicio de este capítulo. Para la segunda, cada fila se ha desplazado un lugar a la izquierda (en lugar de a la derecha) del que está arriba. Esta construcción realmente funciona para$n$ impar, pero nunca para$n$ par. Por ejemplo$n = 4$, cuando, daría

\[ 1 \; \; 2 \; \; 3\;\;4 \;\;\;\;\;\;\;\;\;\;\;\; 1\;\;2\;\;3\;\;4 \\ 4 \; \; 1 \; \; 2\;\;3 \;\;\;\;\;\;\;\;\;\;\;\; 2\;\;3\;\;4\;\;1 \\ 3 \; \;4\;\; 1 \; \; 2 \;\;\;\;\;\;\;\;\;\;\;\; 3\;\;4\;\;1\;\;2 \\ 2 \; \; 3 \; \;4\;\; 1 \;\;\;\;\;\;\;\;\;\;\;\; 4\;\;1\;\;2\;\;3 \]

Se puede ver que el par ordenado$(1, 1)$ ocurre en dos posiciones: fila$1$, columna$1$, y fila$3$, columna$3$. Por lo que este par de cuadrados latinos definitivamente no es ortogonal. De hecho, el primero de estos cuadrados no tiene un cuadrado latino que sea ortogonal a él. Sin embargo, hay un par de ortogonales

Cuadrados latinos de orden$4$:

\[ 1 \; \; 2 \; \; 3\;\;4 \;\;\;\;\;\;\;\;\;\;\;\; 1\;\;2\;\;3\;\;4 \\ 3 \; \;4\;\; 1 \; \; 2 \;\;\;\;\;\;\;\;\;\;\;\; 4 \; \;3\;\; 2 \; \; 1 \\ 4 \; \;3\;\; 2 \; \; 1 \;\;\;\;\;\;\;\;\;\;\;\; 2 \; \; 1 \; \;4\;\; 3 \\ 2 \; \; 1 \; \;4\;\; 3 \;\;\;\;\;\;\;\;\;\;\;\; 3 \; \;4\;\; 1 \; \; 2 \]

Definición: Mutuamente ortogonal

Un conjunto de cuadrados latinos es mutuamente ortogonal si cada par distinto de cuadrados latinos en el conjunto son ortogonales. Llamamos a tal conjunto, un conjunto de MOLS (para Cuadrados Latinos Mutuamente Ortogonales).

La pregunta natural que se plantea en este contexto es, ¿cuántos cuadrados latinos puede haber en un conjunto de MOLS?

Antes de intentar responder a esta pregunta, notemos que si tenemos un par de cuadrados latinos ortogonales y permutamos los símbolos utilizados en el conjunto$N$ independientemente para cada uno de los cuadrados (dando como resultado nuevos cuadrados latinos que no obstante son esencialmente los mismos, como se discute en la Sección 16.1), el resultante par de cuadrados latinos seguirán siendo ortogonales. Si en el primer cuadrado el símbolo se$x$ mapea al símbolo$y$, y en el segundo cuadrado el símbolo se$u$ mapea al símbolo$v$, entonces en el nuevo par de cuadrados latinos el par ordenado$(y, v)$ aparecerá precisamente una vez, ya que el par ordenado$(x, u)$ apareció precisamente una vez en el par original de cuadrados latinos. Esto es cierto para cualquier par de entradas$(y, v)$, por lo que cada par de entradas debe aparecer precisamente una vez.

Esta idea de que podemos permutar independientemente los símbolos en cada cuadrado, nos lleva a un método muy agradable de representar MOLS. La idea clave es que no es necesario usar el mismo conjunto de símbolos para cada cuadrado, ya que los símbolos que elegimos se pueden permutar de forma independiente para que coincidan entre sí. De hecho, no necesitamos usar símbolos en absoluto para representar algunos de los cuadrados; podemos variar alguna otra característica. Por ejemplo, para representar los dos cuadrados ortogonales latinos de orden$3$ que se mostraron en el Ejemplo 16.2.1, podemos usar los símbolos$1$$3$ para representar el primer cuadrado, y los colores rojo (para$1$), azul (para$2$) y verde (para$3$) para representar el segundo cuadrado. Sin embargo, no es factible variar los colores en este libro de texto, que está impreso en blanco y negro. En cambio, para el segundo cuadrado, usemos “inclinado a la izquierda” (para$1$), “recto hacia arriba” (para$2$) e “inclinado hacia la derecha” (para$3$). Entonces (por ejemplo) ya que en la segunda fila, tercera columna la primera plaza tenía a$2$ y la segunda tenía a$1$, colocamos una$2$ que se inclina hacia la izquierda en esa ubicación en nuestra nueva representación (inclinada a la izquierda porque la entrada de la segunda plaza era$1$; y$2$ porque esa fue la entrada de la primera plaza). Aquí está la representación completa:

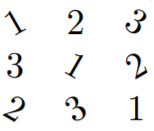
$clipboard_e97898ad4201b659d00544c441143a08e.png$

Por la propiedad de ortogonalidad, ¡cada combinación de inclinación y número debe aparecer exactamente en una posición! Aún más sorprendente, si tenemos un conjunto de MOLS y variamos diferentes parámetros para cada uno de los cuadrados, el hecho de que los cuadrados sean todos mutuamente ortogonales significará que cada combinación de los parámetros aparece exactamente en una posición. Por ejemplo, si tenemos un conjunto de cinco MOLS, podríamos colocar una forma coloreada detrás de cada símbolo coloreado, y tener diferentes números de copias del símbolo. Para cualquier posible color de cualquier forma posible que aparezca detrás de cualquier número posible de cualquier color posible de cualquier símbolo posible, ¡podrías encontrar una posición en la que aparezca esa combinación!

Esta aproximación al MOLS es esencialmente el contexto en el que surgieron por primera vez, como podemos ver en el ejemplo de Euler de los oficiales. Para los dos cuadrados latinos ortogonales buscados en su pregunta, los símbolos en uno representan las filas mientras que los símbolos en el otro representan al regimiento. En su casilla final, cada oficial podría estar representado por un par de símbolos que indicaran su rango y su regimiento —o por una letra para su regimiento y un color para su rango.

Aquí hay una respuesta parcial a la pregunta de cuántos MOLS de orden puede$n$ haber:

Teorema$\PageIndex{1}$

Si$S$ es un conjunto de MOLS de orden$n$, entonces$|S| ≤ n − 1$.

Prueba

Eso podemos suponer$N = \{1, . . . , n\}$. En cada una de las casillas latinas en$S$, podemos permutar independientemente los símbolos de$N$. Como se señaló anteriormente, el resultado seguirá siendo un conjunto de MOLS. Permutamos los símbolos para que la primera fila de cada uno de los cuadrados latinos tenga las entradas$1, 2, . . . , n$ en ese orden.

Ahora bien, si tomamos alguno$i ∈ N$ y consideramos algún par de los cuadrados latinos, el par ordenado$(i, i)$ aparece en algún lugar de la primera fila. Considera la primera entrada de la segunda fila en cada cuadrado de$S$. Ninguna de estas entradas puede serlo$1$, ya que ya$1$ ha aparecido en la primera columna de cada una de las casillas latinas. No hay dos de los cuadrados latinos que puedan tener la misma entrada$j$ en esta posición, ya que el par ordenado$(j, j)$ ya apareció en la$j^{\text{th}}$ posición de la primera fila de este par de cuadrados, por lo que no puede volver a aparecer en la primera posición de la segunda fila. Entonces no puede haber más cuadrados en$S$, que las$n − 1$ distintas entradas de$N \setminus \{1\}$ eso podrían entrar en esta posición. Así,$|S| ≤ n − 1$, como se afirma.

La siguiente pregunta natural es, ¿es posible lograr$n − 1$ MOLS de orden$n$? Ya hemos visto que la respuesta es sí en un caso muy pequeño, ya que encontramos$2$ MOLS de orden$3$. De hecho, hay infinitamente muchos valores de$n$ para los que hay$n − 1$ MOLS de orden$n$.

El siguiente resultado se puede generalizar a poderes primos usando alguna teoría básica de campo que debes entender si has tomado Matemáticas$3400$. No obstante, para los efectos de este curso, evitaremos la teoría explícita de campo y demostraremos el resultado sólo para primos.

Requerimos un poco de aritmética modular para este resultado. Como la aritmética modular también será útil para algunos de nuestros resultados posteriores, aquí hay una revisión rápida de algunos puntos clave.

Definición: Modulo$n$

Realizar cálculos módulo$n$ significa reemplazar el resultado con el resto que obtendría al dividir ese resultado por$n$. En otras palabras, si el resultado de un cálculo es$n$ o mayor, sustituya el resultado por su resto al dividirlo por$n$.

Notación

Si$a$ y$b$ tenemos el mismo resto tras la división por$n$, entonces escribimos$a ≡ b$ (mod$n$).

Hay dos hechos clave de la aritmética modular que vamos a requerir. El primero es que si$a ≡ b$ (mod$n$) y$0 ≤ a$$b < n$,, entonces debemos tener$a = b$.

El otro es que si$qa ≡ qb$ (mod$n$) y$n$ y$q$ tienen un mayor divisor común de$1$, entonces$a ≡ b$ (mod$n$). En el caso especial donde$n$ es primo, siempre y cuando no$q$ sea un múltiplo de$n$ entonces$n$ y siempre$q$ tendrá un mayor divisor común de$1$.

Teorema$\PageIndex{2}$

Para cualquier prime$p$, hay$p − 1$ MOLS de orden$p$.

Prueba

Vamos a utilizar$N = \{0, . . . , p−1\}$. Para asegurar que los resultados de nuestros cómputos estarán en$N$, todos los cálculos dados en este resultado deben ser tomados módulo$p$.

Serán las plazas$\{S_1, . . . , S_{p−1}\}$. Para$k ∈ \{1, . . . , p\}$,

\[S_k=\left[ \begin{array}{ll} 0 & 1 & ... &p-1\\ k & k+1 & ... &k + (p − 1)\\ 2k & 2k+1 & ... &2k + (p − 1)\\ ... & ... & ... &...\\ (p − 1)k & (p − 1)k + 1 & ... &(p − 1)k + (p − 1)\\ \end{array} \right] \]

Primero verificamos que cada uno$S_k$ es un cuadrado latino. Las entradas en cada fila se ven fácilmente como distintas. Si las entradas en la primera columna son distintas, entonces podemos ver que las entradas en cada otra columna serán distintas. Supongamos que$0 ≤ i$,$j ≤ p − 1$ y eso$ik ≡ jk$ (mod$p$). Entonces como cada uno$k ∈ \{1, . . . , p − 1\}$ tiene un mayor divisor común de$1$ con$p$, vemos que$i ≡ j$ (mod$p$). Ya que$0 ≤ i$,$j ≤ p − 1$, esto obliga$i = j$. Entonces las entradas en la primera columna de$S_k$ son todas distintas. Así, cada$S_k$ es un cuadrado latino.

Supongamos que para algunos$1 ≤ i$$j ≤ p − 1$,, los cuadrados$S_i$ y$S_j$ tienen el mismo par ordenado en dos posiciones: fila$k_1$, columna$m_1$, y fila$k_2$, columna$m_2$. Entonces por las fórmulas dadas para las entradas de cada cuadrado latino, debemos tener

\[ \begin{equation} \begin{split} (k_1 − 1)i + m_1 − 1 &≡ (k_2 − 1)i + m_2 − 1 (\text{mod } p), \\ \text{and } (k_1 − 1)j + m_1 − 1 &≡ (k_2 − 1)j + m_2 − 1 (\text{mod } p), \\ \text{Thus, } k_1i + m_1 &≡ k_2i + m_2 (\text{mod } p), \\ \text{and } k_1j + m_1 &≡ k_2j + m_2 (\text{mod } p), \\ \text{Therefore, } m_2 − m_1 ≡ k_2i − k_1i &= (k_2 − k_1)i ≡ k_2j − k_1j = (k_2 − k_1)j \;(\text{mod } p). \end{split} \end{equation} \]

Desde$(k_2 − k_1)i ≡ (k_2 − k_1)j$ (mod$p$), y$1 ≤ i$$j ≤ p − 1$, ya sea$i = j$ (así que elegimos el mismo cuadrado latino dos veces en lugar de elegir un par de cuadrados latinos distintos), o$k_2 −k_1 ≡ 0$ (mod$p$). Ya que$k_1$ y$k_2$ son números de fila, están entre$1$ y$p$ así esto obliga$k_1 = k_2$. Además, en este caso también debemos tener$m_2 − m_1 ≡ 0$ (mod$p$), y vemos que esto también obliga$m_1 = m_2$. Así, las dos posiciones en las que aparecía la misma pareja ordenada, eran en realidad la misma posición elegida dos veces.

Esto demuestra que efectivamente$\{S_k | 1 ≤ k ≤ p − 1\}$ es un conjunto de$p − 1$ MOLS.

Ejemplo$\PageIndex{2}$

Aquí están los primeros$8$ de los$10$ MOLS de orden$11$, encontrados usando la fórmula dada en la prueba anterior.

\[ 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \\ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \;\;\;\;\;\;\;\;\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \\ 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \\ 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \;\;\;\;\;\;\;\;\;\; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \\ 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \;\;\;\;\;\;\;\;\;\; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \\ 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \;\;\;\;\;\;\;\;\;\; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \\ 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \\ 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;\;\;\;\;\;\;\;\; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \\ 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \;\;\;\;\;\;\;\;\;\; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \\ 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \;\;\;\;\;\;\;\;\;\; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \;\;\;\;\;\;\;\;\;\; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \\[0.5in] 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \\ 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \\ 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \\ 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\\ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \;\;\;\;\;\;\;\;\;\; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \\ 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \;\;\;\;\;\;\;\;\;\; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \\ 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;\;\;\;\;\;\;\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \\ 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \;\;\;\;\;\;\;\;\;\; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \\ 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;\;\;\;\;\;\;\;\; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \\ 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \;\;\;\;\;\;\;\;\;\; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \\ 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \;\;\;\;\;\;\;\;\;\; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \\[0.5in] 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \\ 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \;\;\;\;\;\;\;\;\;\; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \\ 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \\ 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \;\;\;\;\;\;\;\;\;\; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \;\;\;\;\;\;\;\;\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\\ 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \;\;\;\;\;\;\;\;\;\; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \\ 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \;\;\;\;\;\;\;\;\;\; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \\ 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;\;\;\;\;\;\;\;\; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \\ 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \\ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \;\;\;\;\;\;\;\;\;\; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \\ 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \\[0.5in] 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \;\;\;\;\;\;\;\;\;\; 0\; \; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10 \\ 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;\;\;\;\;\;\;\;\; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \\ 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \;\;\;\;\;\;\;\;\;\; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \\ 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \;\;\;\;\;\;\;\;\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \\ 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \;\;\;\;\;\;\;\;\;\; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\; 7\; \; 8\; \; 9 \\ 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;\;\;\;\;\;\;\;\; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \\ 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \;\;\;\;\;\;\;\;\;\; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \\ 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \; 2\; \; 3\; \; 4 \;\;\;\;\;\;\;\;\;\; 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \\ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0 \;\;\;\;\;\;\;\;\;\; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7\; \; 8 \\ 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5\; \; 6 \;\;7 \;\;\;\;\;\;\;\;\;\; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \;\;2\; \; 3\; \; 4\; \; 5 \\ 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1\;\;2\;\;3 \;\;\;\;\;\;\;\;\;\; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8\; \; 9\; \; 10\;\; 0\;\; 1 \; \;2 \\ \]

Ahora hemos visto que es posible encontrar$p − 1$ MOLS de orden$p$ para cualquier prime$p$, y que la prueba se puede generalizar a los poderes primos. Sin embargo, como ya hemos discutido en relación con el problema original de Euler, hay órdenes para las que no se$n$ puede lograr el encuadernado de$n − 1$ MOLS de orden: de hecho, para el orden no$6$ es posible ni siquiera encontrar un par de cuadrados latinos ortogonales.

Si te interesa o estás familiarizado con alguna geometría finita, la existencia de$n − 1$ MOLS de orden$n$ equivale a la existencia de un plano de orden proyectivo$n$. Los planos proyectivos, a su vez, son un tipo especial de diseño. Para un interesante artículo sobre algunas de estas relaciones, consulte https://www.maa.org/sites/default/files/pdf/upload_library/22/Ford/Lam305-318.pdf. También hay alguna información al respecto en las Secciones 18.3 y 18.4.

Ejercicio$\PageIndex{1}$

1) Encuentra los dos MOLS de orden$11$ que no están incluidos en el Ejemplo 16.2.2, pero son ortogonales entre sí y a los cuadrados que ahí se enumeran.

2) Encontrar un tercer cuadrado latino de orden$4$ que sea ortogonal a ambos de los cuadrados latinos ortogonales de orden$4$ que se dieron anteriormente en esta sección.

3) Aquí hay un cuadrado latino de orden$8$, y algunas entradas para un segundo cuadrado latino de orden$8$. Completar el segundo cuadrado para obtener un par de cuadrados latinos ortogonales.

\[ 1\; \; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8 \;\;\;\;\;\;\;\;\;\; 1\;\; 2\; \; 3\; \; 4\; \; 5\; \; 6\; \; 7\; \; 8 \\ 2\; \; 1\; \; 4\; \; 3\; \; 6\; \; 5\; \; 8\; \; 7 \;\;\;\;\;\;\;\;\;\; 3\; \; 4\; \; \_\; \; \_\; \; \_\; \; 8\; \; 5\;\; 6 \\ 3\; \; 4\; \; 1\; \; 2\; \; 7\; \; 8\; \; 5\; \; 6 \;\;\;\;\;\;\;\;\;\; 5\; \; \_\; \; 7\; \; \_\; \; \_\;\; 2\;\; 3 \;\;\_ \\ 4\; \; 3\; \; 2\; \; 1\; \; 8\; \; 7\; \; 6\;\; 5 \;\;\;\;\;\;\;\;\;\; 7\; \; \_\; \; \_\;\; 6\;\; \_ \;\;\_\; \; \_\; \; \_ \\ 5\; \; 6\; \; 7\; \; 8\; \; 1\; \; 2\;\; 3\;\; 4 \;\;\;\;\;\;\;\;\;\; 4\;\; \_\;\; \_ \;\;1\; \; 8\; \; \_\; \; \_\; \; \_ \\ 6\; \; 5\; \; 8\; \; 7\; \; 2\;\; 1\;\; 4 \;\;3 \;\;\;\;\;\;\;\;\;\; 2\; \; \_\; \; \_\; \; \_\; \; \_\; \; 5\; \; \_\; \; \_ \\ 7\; \; 8\; \; 5\; \; 6\;\; 3\;\; 4 \;\;1\; \; 2 \;\;\;\;\;\;\;\;\;\; 8\; \; \_\; \; \_\; \; \_\; \; \_\; \; \_\; \; \_\; \; 1\\ 8\; \; 7\; \; 6\;\; 5\;\; 4 \;\;3\; \; 2\; \; 1 \;\;\;\;\;\;\;\;\;\; 6\; \; \_\; \; \_\; \; 7\; \; \_\; \; \_\;\; \_\;\; 3\\ \]

4) Anotar los seis cuadrados latinos mutuamente ortogonales$S_1, . . . , S_6$ de orden$7$ que se construyen dejando$p = 7$ entrar la prueba del Teorema 16.2.2.