Apéndice A: Soluciones a ejercicios seleccionados

Soluciones al Ejercicio 2.1.1

1) Hay\(4\) opciones de color;\(2\) opciones para aire acondicionado;\(5\) opciones para estéreo; y\(3\) opciones para tapetes de piso. Entonces en total, hay\(4 · 2 · 5 · 3 = 120\) diferentes combinaciones de opciones. De estas,\(3\) las combinaciones están disponibles en el concesionario, por lo que la probabilidad de que uno de estos autos tenga las opciones que quiere es\(\dfrac{3}{120} = \dfrac{1}{40}\).

2) En el libro de Candyce, el lector tendrá\(3\) opciones en el primer punto de decisión, y\(2\) opciones en cada uno de los siguientes tres puntos de decisión. Así, hay un total de\(3 · 2 · 2 · 2 = 3 · 2^3 = 24\) posibles historias. Candyce debe escribir\(24\) terminaciones.

Soluciones al Ejercicio 2.2.1

1) Llamemos a los marcadores negros Negro A, Negro B y Negro C. Las cuatro opciones posibles son: Dejo atrás el marcador azul; dejo atrás Negro A; dejo atrás Negro B; dejo atrás Negro C. En cada uno de los últimos tres casos, tomo el marcador azul. Por lo tanto, la probabilidad de que tome el marcador azul es\(\dfrac{(1 + 1 + 1)}{4} = \dfrac{3}{4}\).

2) Si Maple está pensando en una letra, hay\(26\) cosas en las que podría estar pensando. Si está pensando en un dígito, hay\(10\) cosas en las que podría estar pensando. En total, hay\(10 + 26 = 36\) cosas en las que podría estar pensando.

Soluciones al Ejercicio 2.3.1

1) Dividimos las posibles contraseñas en tres casos, dependiendo de si el dígito está en la primera, segunda o tercera posición. En cada caso, tenemos\(10\) opciones para el dígito,\(26\) opciones para la primera letra minúscula y\(26\) opciones para la segunda letra minúscula. Así, en cada caso, tenemos\(10 · 262\) posibles contraseñas. En total, existen\(10·262+10·262+10·262 = 30·262 = 20280\) diferentes contraseñas con estas restricciones.

2) Dividimos las posibles contraseñas en dos casos, dependiendo de si existen\(8\) o\(9\) caracteres. Si hay\(8\) caracteres, entonces la regla del producto nos dice que hay\(10^8\) contraseñas que consisten enteramente en dígitos (\(10\)opciones para el dígito en cada una de las\(8\) posiciones). De igual manera, si hay\(9\) caracteres, entonces hay\(10^9\) contraseñas que constan enteramente de dígitos. En total, hay\(10^8 + 10^9 = 1,100,000,000\) contraseñas con estas restricciones.

Soluciones al Ejercicio 2.4.1

A veces es posible convertir un uso de la regla de suma en un uso de la regla del producto, o viceversa, por lo que podría obtener diferentes respuestas que podrían ser correctas. Las respuestas a continuación representan una forma natural de resolver cada problema.

1) Utilizar ambas reglas. Hay dos casos que deben sumarse: el número de números que tienen dos dígitos, y el número de números que tienen cuatro dígitos. Para cada uno de estos casos, use la regla del producto para determinar cuántos números tienen esta propiedad. (La respuesta es\(9 · 10 + 9 · 10^3 = 9090\). Tenga en cuenta que para que un número tenga exactamente\(k\) dígitos, el dígito inicial no puede ser cero.)

2) Utilice solo la regla del producto. Hay\(6\) resultados del dado rojo, y para cada uno de estos, hay\(6\) resultados del dado amarillo, para un total de\(6 · 6 = 36\) resultados.

Soluciones al Ejercicio 3.1.1

1) La banda podrá elegir a cualquiera de las\(6\) personas para tocar la guitarra principal. Entonces podrán elegir a cualquiera de las\(5\) personas restantes para tocar el bajo. Por lo tanto, la banda se puede completar\(6 · 5 = 30\) de maneras. También podrías observar que el número de formas de completar la banda es el número de\(2\) -permutaciones (para los dos espacios abiertos) de\(6\) personas, que es\(6 · . . . · (6 − 2 + 1) = 6 · 5 = 30\).

2) Divide esto en dos casos, dependiendo de cuál de las dos partes obtuvo Garth. Si consiguió la primera parte, entonces había\(8\) otras personas compitiendo por\(4\) otros papeles, por lo que la cantidad de formas de completar el elenco en este caso es el número de\(4\) -permutaciones de la\(8\) gente. Repitiendo este argumento para el segundo caso (si Garth obtuvo la otra parte) y sumando los dos números, vemos que en total hay\(2 · 8 · 7 · 6 · 5\) (ya\(8−4 + 1 = 5\)) formas de completar el elenco. Esto funciona para\(3360\).

Soluciones al Ejercicio 3.2.1

2) Al final de este truco, los únicos juegos de cartas con los que no podría terminar son conjuntos que no contienen más que espadas. Hay\(\binom{13}{3}\) conjuntos que incluyen solo espadas (elige cualquiera\(3\) de las\(13\) espadas), y\(\binom{52}{3}\) posibles conjuntos de\(3\) cartas de la baraja en su conjunto, por lo que el número de conjuntos de tres cartas que no son todas picas es\(\binom{52}{3} − \binom{13}{3} = 22100 − 286 = 21814\).

3) El dígito a la cabeza no puede ser un cero, así que si va a haber exactamente dos ceros, tenemos\(4\) posibles posiciones en las que se pueden colocar. Así, hay\(\binom{4}{2}\) formas de elegir dónde colocar los dos ceros. En cada una de las tres posiciones restantes, podemos colocar cualquiera de los dígitos\(1\) a través\(9\), por lo que hay\(93\) opciones para los dígitos restantes. Así, hay números\(\binom{4}{2}\)\(\dfrac{9}{3} = 4374\)\(5\) -dígitos que contienen exactamente dos ceros.

Soluciones al Ejercicio 3.3.1

2) Usando el Teorema Binomial, vemos que

\((a + b)^5 (c + d)^6 = \left( \sum_{r=0}^{5} \binom{5}{r} a^rb^{5-r} \right) \left( \sum_{s=0}^{6} \binom{6}{s} c^sd^{6-s} \right) \).

Para encontrar el coeficiente de\(a^2 b^3 c^2 d^4\), debemos tomar\(r = 2\) y\(s = 2\). Esto nos da el término\(\binom{5}{2} a^2 b^3 \binom{6}{2} c^2 d^4 = \binom{5}{2} \binom{6}{2} a^2 b^3 c^2 d^4\). Así, el coeficiente de\(a^2 b^3 c^2 d^4\) es\(\binom{5}{2} \binom{6}{2} = 10 · 15 = 150\).

4) Usando el Teorema Binomial, vemos que

\((a + b)^5 (c + d)^6 = \sum_{r=0}^{5} \binom{5}{r} a^rb^{5-r} + \sum_{s=0}^{4} \binom{4}{s} c^sd^{4-s} \).

El coeficiente de\(a^3 b^2\) en el primer summand surge cuando\(r = 3\); en el segundo summand, surge cuando\(s = 3\). Esto nos da el término\(\binom{5}{3} a^3 b^2 + \binom{4}{3} a^3 (b^2)^1\). Así, el coeficiente de\(a^3 b^2\) es\(\binom{5}{3} + \binom{4}{3} = 10 + 4 = 14\).

Soluciones al Ejercicio 4.1.3

1) Al contar el número de subconjuntos de un\(n\) -set, vimos que existe una biyección entre ese número y el número de cadenas binarias de longitud\(n\): identificar cada elemento del conjunto con una posición en la cadena, y poner a\(0\) en esa posición si el elemento no está en el subconjunto, y a\(1\) si lo es. Análogamente, podemos encontrar una biyección entre el número de estas estructuras y el número de cadenas ternarias de longitud\(n\) (cadenas que contienen\(0\),\(1\), o\(2\) en cada posición). Identificar cada elemento del conjunto con una posición en la cadena, poner a\(0\) en esa posición si el elemento no está en la estructura, a\(1\) si ocurre una vez, y a\(2\) si ocurre dos veces. Así, podemos formar\(3n\) estructuras a partir del conjunto\(\{1, . . . , n\}\): hay\(3\) opciones para cada una de las\(n\) entradas en la cadena ternaria.

3) Identificamos a cada uno de los diez contendientes olímpicos con una cuna, y cada una de las tres muñecas con una de las tres medallas. Si la muñeca correspondiente a la medalla de oro entra en cuna\(i\), ésta corresponde al competidor correspondiente a cuna\(i\) ganando la medalla de oro. De igual manera, si el muñeco correspondiente a la medalla de plata va a la cuna\(j\), esto equivale a que el contendiente correspondiente a cuna\(j\) gane la medalla de plata; y el muñeco correspondiente al bronce que va a la cuna\(k\) es equivalente al contendiente correspondiente a cuna\(k\) ganando la medalla de bronce.

Soluciones al Ejercicio 4.2.2

2) COMBINATORIA. Utilizamos el problema que se nos da en la pista, así que estará contando el número de formas de comenzar con\(n\) perros, determinar\(r\) quién entrará en una competencia y\(k\) de los que serán finalistas.

Soluciones al Ejercicio 4.2.3

1) Podríamos usar esta expresión para contar el número de formas de elegir un líder y algún número (que podría ser cero) de otros miembros del equipo para un proyecto, de un grupo de\(n\) personas. Hay\(n\) formas de elegir al líder, y para cada una de estas, hay\(2^{n−1}\) formas de elegir un subconjunto de las otras\(n − 1\) personas para que sean miembros del equipo.

3) Podríamos usar esta expresión para contar el número de formas de comenzar con una colección de\(n\) libros, elegir\(r\) libros para poner en estanterías y algún otro número (que podría ser cero) de otros libros para guardar pero no exhibir. Lo desglosamos en casos dependiendo del número total\(k\) de libros que se guardan (incluidos los libros que se muestran), que podrían estar en cualquier lugar desde\(r\) hasta\(n\). Tomaremos la suma de todas las respuestas. En cada caso, hay\(\binom{n}{r}\) formas de elegir los\(k\) libros a conservar, y para cada una de esas opciones, hay\(\binom{k}{r}\) formas de elegir los\(r\) libros a exhibir de los libros que se guardan. Así, hay un total de\(\sum_{k=r}^{n} = \binom{n}{r} \binom{k}{r}\) soluciones a este problema.

Soluciones al Ejercicio 5.1.1

2) Hay\(6^3\) formas para que se elijan los regalos del maestro (cada niño puede elegir cualquiera de los seis tipos de premios para darle a su maestro). Hay\(\left( \binom{6}{3} \right)\) formas para que Kim elija sus otros tres premios;\(\left( \binom{6}{2} \right)\) formas para que Jordan elija sus otros dos premios, y\(\left( \binom{6}{5} \right)\) formas para que Finn elija sus otros cinco premios. Así, el número total de formas para que se elijan los premios (incluidos los obsequios de maestros) es

\(\begin{equation} \begin{split} 6^3 \left( \binom{6}{3} \right)\left( \binom{6}{2} \right)\left( \binom{6}{5} \right) &= 6^3 \binom{6+3-1}{3} \binom{6+2-1}{2} \binom{6+5-1}{5} \\[0.25in] &= 6^3 \binom{8}{3} \binom{7}{2} \binom{10}{5} \\[0.25in] &= 6^3· 56 · 21 · 252 = 64,012,032 \end{split} \end{equation}\)

3) Dado que los jueces deben elegir al menos un proyecto de cada grupo de edad, esto equivale a un problema en el que están eligiendo sólo seis proyectos para avanzar, sin restricciones sobre cómo los eligen. Pueden elegir seis proyectos de tres categorías en\(\left( \binom{3}{6} \right) = \binom{3 + 6 − 1}{6} = \binom{8}{6} = 28\) formas.

Soluciones al Ejercicio 5.1.2

1) COMBINATORIA. Contaremos el número de formas de elegir\(k\) elementos de un menú que tenga\(n\) diferentes entradas (incluyendo macarrones y queso), de dos maneras.

Soluciones al Ejercicio 5.2.1

1) Hay\(14\) palabras en la lista. La palabra “el” aparece tres veces; las palabras “on” y “child” aparecen dos veces cada una; las otras siete palabras aparecen una vez cada una. Así, el número de “poemas” (ordenamientos del conjunto) es

\(\binom{14}{3, 2, 2, 1, 1, 1, 1, 1, 1, 1} = \dfrac{14!}{3!2!2!} = 3,632,428,800\).

Soluciones al Ejercicio 6.1.1

1) Son posibles diversas fórmulas. Lo más simple es que la secuencia puede ser descrita por la relación de recurrencia\(s_1 = 4\),\(s_i = 2s_{i−1} + 1\) para\(i ≥ 2\). Con esta descripción, el siguiente término es\(s_5 = 2(39) + 1 = 79\).

3) Ajustando la relación de recurrencia del Ejemplo 6.1.3, obtenemos la nueva relación

\(r_n = r_{n−1} − 20 + .01(r_{n−1} − 20).\)

Esto simplifica a Todavía\(r_n = 1.01(r_{n−1} − 20).\) tenemos\(r_0 = 2000\). Ahora tenemos

\(r_1 = 1.01(r_0 − 20) = 1.01(1980) = 1999.80\).

Stavroula está perdiendo (marginalmente) dinero desde el principio. Esta situación sólo empeorará a medida que su saldo inicial cada año vaya menguando.

Soluciones al Ejercicio 6.2.1

1) PRUEBA. Caso base:\(n = 1\). Tenemos\(b_1 = 5\) y\(5 + 4(1 − 1) = 5\), así\(b_n = 5 + 4(n − 1)\) cuando\(n = 1\).

Paso inductivo: Comenzamos con la hipótesis inductiva. Seamos\(k ≥ 1\) arbitrarios, y supongamos que la igualdad se mantiene para\(n = k\); es decir, asuma eso\(b_k = 5 + 4(k − 1)\). Ahora queremos deducir que

\(b_{k+1} = 5 + 4(k + 1 − 1) = 5 + 4k\).

Usando la relación recursiva, tenemos\(b_{k+1} = b_k + 4\) desde entonces\(k + 1 ≥ 2\). Usando la hipótesis inductiva, tenemos\(b_k = 5 + 4(k − 1)\). Armando estos da

\(b_{k+1} = 5 + 4(k − 1) + 4 = 5 + 4k − 4 + 4 = 5 + 4k = 5 + 4(k + 1 − 1),\)

según se desee. Esto completa la prueba del paso inductivo.

Por el Principio de Inducción Matemática,\(b_n = 5 + 4(n − 1)\) para cada\(n ≥ 1\).

3) PRUEBA. Caso base:\(n = 0\). Tenemos\(0! = 1\) (por definición) y\(n = 0\), entonces\(n! = 1 ≥ 0 = n\). Así,\(n! ≥ n\) cuando\(n = 0\).

Paso inductivo: Comenzamos con la hipótesis inductiva. Seamos\(k ≥ 0\) arbitrarios, y supongamos que la desigualdad se sostiene\(n = k\); es decir, asuma eso\(k! ≥ k\). Ahora queremos deducir eso\((k + 1)! ≥ k + 1\). Usando la definición de factorial, tenemos\((k + 1)! = (k + 1)k!\) desde entonces\(k + 1 ≥ 0 + 1 = 1\). Usando la hipótesis inductiva, tenemos\(k! ≥ k\). Armando estos da

\((k + 1)! = (k + 1)k! ≥ (k + 1)k\).

Si\(k ≥ 1\), entonces

\((k + 1)k ≥ (k + 1)1 = k + 1\)

y estamos hechos. Si\(k = 0\), entonces\((k + 1)! = 1! = 1 = k + 1\).

Por el Principio de Inducción Matemática,\(n! ≥ n\) para cada\(n ≥ 0\).

Soluciones al Ejercicio 6.3.1

2) PRUEBA. Casos base: Tendremos cuatro casos base:\(n = 12\),\(n = 13\),\(n = 14\), y\(n = 15\).

Para\(n = 12\), puedo\($12\) ingresar a mi tarjeta regalo comprando tres incrementos de\($4\), ya que\(4 + 4 + 4 = 12\).

Para\(n = 13\), puedo\($13\) ingresar a mi tarjeta regalo comprando dos incrementos de\($4\) y uno de\($5\), ya que\(4 + 4 + 5 = 13\).

Para\(n = 14\), puedo\($14\) ingresar a mi tarjeta regalo comprando dos incrementos de\($5\) y uno de\($4\), ya que\(4 + 5 + 5 = 14\).

Para\(n = 15\), puedo\($15\) ingresar a mi tarjeta regalo comprando tres incrementos de\($5\), ya que\(5 + 5 + 5 = 15\).

Paso inductivo: Comenzamos con la hipótesis inductiva (fuerte). \(k ≥ 15\)Sea arbitrario, y asuma que por cada entero\(i\) con\(k − 3 ≤ i ≤ k\), puedo poner\($i\) en mi tarjeta regalo.

Ahora quiero deducir que puedo poner\($(k+1)\) en mi tarjeta regalo. Usando la hipótesis inductiva en el caso\(i = k − 3\), veo que add puede\($(k − 3)\) poner en mi tarjeta regalo comprando incrementos de\($4\) o\($5\). Ahora bien, si compro un incremento adicional de\($4\), he puesto un total de\($(k − 3 + 4) = $(k + 1)\) en mi tarjeta regalo, según se desee. Esto completa la prueba del paso inductivo.

Por el (fuerte) Principio de Inducción Matemática, puedo poner cualquier cantidad de dólares que sea al menos\($12\) en mi tarjeta regalo.

Soluciones al Ejercicio 7.1.1

2) Dado que el enésimo término de la secuencia es\(2n\), la función generadora es\(\sum_{n=0}^{\infty} 2^nx^n\).

3) La función generadora es\(1 + 5x + 10x^2 + 15x^3 + 10x^ + 5x^5 + x^6\).

Soluciones al Ejercicio 7.2.1

1) Tenemos\(\binom{−5}{7} = (−1)^7 \binom{5 + 7 − 1}{7} = − \binom{11}{7} = −330\).

2) Por el Teorema del Binomio Generalizado, el coeficiente de\(y^4\) in\((1 + y)^{−2}\) es\(\binom{−2}{4}\), entonces (reemplazando\(y\) con\(−x\)) el coeficiente de\(x^4\) in\((1 − x)^{−2}\)/es

\((−1)^4 · \binom{−2}{4} = (1) · \dfrac{(−2)(−3)(−4)(−5)}{4!} = 5\).

Soluciones al Ejercicio 7.3.1

1) PRUEBA. Caso base:\(n = 1\). El lado izquierdo de la ecuación en este caso es\(1+x\). El lado derecho es\(\dfrac{1 − x^2}{1 − x}\). Ya que\(1 − x^2 = (1 − x)(1 + x)\), podemos reescribir el lado derecho como\(\dfrac{(1 − x)(1 + x)}{1 − x}\). Cancelando el\(1 − x\) desde la parte superior e inferior da\(1 + x\), por lo que los dos lados son iguales. Ya que una función generadora es un objeto formal,\(x\) está actuando como marcador de posición, y no necesitamos preocuparnos por la posibilidad de\(1 − x = 0\) que eso nos impida cancelar estos factores. Paso inductivo:\(k ≥ 1\) Sea arbitrario, y supongamos que

\(1 + · · · + x^k = \dfrac{1 − x^{k+1}}{1 − x}.\)

Ahora debemos deducir que

\(1 + · · · + x^{k+1} = \dfrac{1 − x^{k+2}}{1 − x}.\)

Tenemos

\(1 + · · · + x^{k+1} = (1 + · · · + x^{k})+ x^{k+1}\)

Aplicando nuestra hipótesis inductiva, esto es\(\dfrac{1 − x^{k+1}}{1 − x} + x^{k+1}\). Sumando esto sobre un denominador común de\(1 − x\) da

\(\dfrac{1 − x^{k+1} + x^{k+1} − x^{k+2}}{1-x} = \dfrac{1-x^{k+2}}{1-x}\)

según se desee.

Por el Principio de Inducción Matemática,

\(1 + · · · + x^n = \dfrac{1-x^{n+1}}{1-x}\)

para cada\(n ≥ 1\).

4) La función generadora para este problema es

\((x + x^2 + x^3 + x^4 + x^5 + x^6 )^5 .\)

Podemos reescribir esto como

\(x^5 (1 + x + x^2 + x^3 + x^4 + x^5 )^5 .\)

Encontrar el coeficiente de\(x^{11}\) en esta expresión es equivalente a encontrar el coeficiente de\(x^6\) in

\((1 + x + x^2 + x^3 + x^4 + x^5 )^5 = \left( \dfrac{1 − x^6}{1 − x} \right)^5.\)

Usando el Teorema Binomial y sustituyendo\(y = −x^6\), vemos que

\(\begin{equation} \begin{split} (1 − x^6)^5 &= (−x^6)^0 + \binom{5}{1} (−x^6)^1 + \binom{5}{2} (−x^6)^2 + \binom{5}{3} (−x^6)^3 + \binom{5}{4} (−x^6)^4 + (−x^6)^5 \\ &= 1 − 5x^6 + 10x^{12} − 10x^{18} + 5x^{24} − x^{30}. \end{split} \end{equation}\)

La función que nos interesa es producto de esto con\((1−x)^{−5}\), y estamos buscando el coeficiente de\(x^6\). Las únicas formas de obtener un\(x^6\) término de este producto son tomando el\(x^0\) término anterior y multiplicándolo por el\(x^6\) término de\((1 − x)^{−5}\), o tomando el\(x^6\) término anterior y multiplicándolo por el\(x^0\) término de\((1 − x)^{−5}\).

Usando el Teorema del Binomio Generalizado (y sustituyendo\(y = −x\)), el coeficiente de\(x^0\) in\((1 − x)^{−5}\) es

\((-1)^0 \binom{-5}{0} = (-1)^0 (-1)^0 \binom{5+0-1}{0} = 1 \)

Del mismo modo, el coeficiente de\(x^6\) in\((1 − x)^{−5}\) es

\((-1)^6 \binom{-5}{6} = (-1)^6 (-1)^6 \binom{5+6-1}{6} = \binom{10}{6} = 210 \)

Así, el número de formas en que Trent puede rodar un total de\(11\) en sus cinco dados es el coeficiente de\(x^{11}\) en nuestra función generadora, que es\(\binom{10}{6} − 5 = 205\). La probabilidad de que esto suceda se\(205\) divide por el número total de resultados de su rollo, que es\(6^5 = 7776\), así\(\dfrac{205}{7776}\), o aproximadamente\(2.5\%\).

Soluciones al Ejercicio 8.1.1

1) Primero reescribimos la función generadora como una suma de dos partes:

\(\dfrac{1}{(1 + 2x)(2 − x)} = \dfrac{A}{1 + 2x} + \dfrac{B}{2-x} = \dfrac{A(2 − x) + B(1 + 2x)}{(1 + 2x)(2 − x)}. \)

Ahora el numerador da\(2A + B + (2B − A)x = 1\) como polinomios. De ahí que debemos tener\(2B − A = 0\) y\(2A + B = 1\). Combinando estos da\(B = \dfrac{1}{5}\) y\(A = \dfrac{2}{5}\). Así, la función generadora dada es igual a

\(\dfrac{2}{5} (1+2x)^{-1} + \dfrac{1}{5} (2-x)^{-1} = \dfrac{2}{5} (1+2x)^{-1} + \dfrac{1}{10} (1- \dfrac{1}{2}x)^{-1} \)

Utilizando el Teorema del Binomio Generalizado, el coeficiente de\(x^r\) en la primera de estas summands es\(\dfrac{2}{5}(−1)^r 2^r\), mientras que el coeficiente de\(x^r\) en la segunda suma lo es\(\dfrac{1}{10} \left( \dfrac{1}{2} \right)^r\). Así, el coeficiente de\(x^r\) es\(\dfrac{2}{5}(−1)^r 2^r + \dfrac{1}{10} \left( \dfrac{1}{2} \right)^r\).

3) Primero reescribimos la función generadora como una suma de tres partes:

\(\begin{equation} \begin{split} \dfrac{1 + 2x}{(1 − 2x)(2 + x)(1 + x)} &= \dfrac{A}{1 − 2x} + \dfrac{B}{2+x} + \dfrac{C}{1+x} \\[0.25in] &= \dfrac{A(2 + x)(1 + x) + B(1 − 2x)(1 + x) + C(1 − 2x)(2 + x)}{(1 − 2x)(2 + x)(1 + x)} \end{split} \end{equation}\)

Ahora el numerador da

\(\begin{equation} \begin{split} & A(2 + 3x + x^2) + B(1 − x − 2x^2) + C(2 − 3x − 2x^2) \\[0.25in] =\;\;& 2A + B + 2C + (3A − B − 3C)x + (A − 2B − 2C)x^2 = 1 + 2x \end{split} \end{equation}\)

como polinomios, así tenemos\(2A + B + 2C = 1\),\(3A − B − 3C = 2\), y\(A − 2B − 2C = 0\). Resolver esto da\(C = \dfrac{−1}{3}\)\(B = \dfrac{3}{5}\),, y\(A = \dfrac{8}{15}\). Así (tomando un factor del\(2\) denominador de la segunda pieza) la función generadora dada es igual a

\(\dfrac{8}{15} (1 − 2x)^{−1} + \dfrac{3}{10} (1 + \dfrac{1}{2}x)^{−1} - \dfrac{1}{3} (1 + x)^{−1}. \)

Utilizando el Teorema del Binomio Generalizado, el coeficiente de\(x^r\) en la primera de estas summands es\(\dfrac{8}{15} 2^r\); el coeficiente de\(x^r\) en la segunda suma es\(\dfrac{3}{10} (−1)^r \left( \dfrac{1}{2} \right)^r\); y el coeficiente de\(x^r\) en la tercera suma es\(−\dfrac{1}{3} (−1)^r\). Concluimos que el coeficiente de\(x^r\) en esta función generadora es

\(\dfrac{8}{15} 2^r = \dfrac{3}{10}(-1)^{r} \left( \dfrac{1}{2} \right)^r - \dfrac{1}{3}(-1)^r\)

Soluciones al Ejercicio 8.2.1.

2) Para utilizar el método de fracciones parciales, primero factorizamos el denominador:

\(2x^2 + x − 1 = (2x − 1)(x + 1).\)

Ahora, escribe

\(\begin{equation} \begin{split} f(x) &= \dfrac{2+x}{2x^2 + x − 1} = \dfrac{2+x}{(2x − 1)(x + 1)} = \dfrac{A}{2x-1} + \dfrac{B}{x+1} \\[0.25in] &= \dfrac{A(x + 1) + B(2x − 1)}{(2x − 1)(x + 1) } = \dfrac{(A − B) + (A + 2B)x}{2x^2 + x − 1} \end{split} \end{equation}\)

Al igualar los coeficientes en los numeradores se obtienen las\(2\) ecuaciones

\(A − B = 2, \;\;\;\; A + 2B = 1.\)

Restar la segunda ecuación de la primera nos dice eso\(−3B = 1\), así\(B = −\dfrac{1}{3}\). Entonces la primera ecuación nos dice eso\(A = 2 − \left( \dfrac{1}{3} \right) = \dfrac{5}{3}\). Así que tenemos

\(f(x) = \dfrac{\dfrac{5}{3}}{2x-1} - \dfrac{\dfrac{1}{3}}{x+1} = \dfrac{\dfrac{5}{3}}{1-2x} - \dfrac{\dfrac{1}{3}}{1+x} \)

El coeficiente de\(x^r\) in\(\dfrac{1}{(1 − x)}\) es\(1\), entonces

• el coeficiente de\(x^r\) in\(\dfrac{1}{(1 − 2x)}\) es\(2^r\) (\(x\)reemplazando por\(2x\)), y
• el coeficiente de\(x^r\) in\(\dfrac{1}{(1 + x)}\) es\((−1)^r\) (reemplazando\(x\) con\(−x\))

Por lo tanto, el coeficiente de\(x^r\) en la función generadora\(f(x)\) es

\(-\dfrac{5}{3}(2^r) -\dfrac{1}{3}(-1)^r\)

Soluciones al Ejercicio 8.3.1

Dejar\(C(x) = \sum_{n=0}^{\infty} c_nx^n\) ser la función generadora de\(\{c_n\}\). Entonces

\(\begin{equation} \begin{split} C(x) &= c_0 &+ c_1x &+ c_2x^2 &+ c_3x^3 &+ c_4x^4 &+ ... \\ xC(x) &= &+ c_0x &+ c_1x^2 &+ c_2x^3 &+ c_3x^4 &+ ... \\ x^2C(x) &= & &+ c_0x^2 &+ c_1x^3 &+ c_2x^4 &+ ... \\ \end{split} \end{equation}\)

por lo

\(\begin{equation} \begin{split} (1 − x − 2x^2)C(x) &= C(x) − xC(x) − 2x^2C(x)\\ &= c_0 + (c_1 − c_0)x + \sum_{n=2}^{\infty} (c_n − c_{n−1} − 2c_{n−2})x^n\\ &= c_0 + (c_1 − c_0)x \end{split} \end{equation} \)

ya que (por la relación de recurrencia) tenemos\(c_n − c_{n−1} − 2c_{n−2} = 0\) para\(n ≥ 2\). Por lo tanto

\(C(x) = \dfrac{c_0 + (c_1 − c_0)x}{1 − x − 2x^2}\)

Desde\(c_0 = 2\) y\(c_1 = 0\), esto significa

\(C(x) = \dfrac{2 + (0 − 2)x}{1 − x − 2x^2} = \dfrac{2-2x}{(1 + x)(1 − 2x)}. \)

Ahora usamos fracciones parciales. Escribir

\(\dfrac{2-2x}{(1 + x)(1 − 2x)} = \dfrac{A}{1+x} + \dfrac{B}{1 − 2x} = \dfrac{A(1 − 2x) + B(1 + x)}{(1 + x)(1 − 2x)} = \dfrac{(A + B) + (B − 2A)x}{(1 + x)(1 − 2x)}. \)

Al igualar los coeficientes en los numeradores se obtienen las ecuaciones

\(2 = A + B,\;\;\;\; −2 = B − 2A.\)

Restar la segunda ecuación de la primera nos dice que

\(2 − (−2) = (A + B) − (B − 2A) = 3A\)

así\(A = \dfrac{4}{3}\). Entonces la segunda ecuación nos dice que

\(B = 2A − 2 = 2\left( \dfrac{4}{3} \right) − 2 = \dfrac{2}{3}.\)

Entonces

\(C(x) = \dfrac{2-2x}{(1 + x)(1 − 2x)} = \dfrac{A}{1+x} + \dfrac{B}{1 − 2x} = \dfrac{\dfrac{4}{3}}{1+x} = \dfrac{\dfrac{2}{3}}{1-2x} = \dfrac{4}{3} \left( \dfrac{1}{1+x} \right) + \dfrac{2}{3} \left( \dfrac{1}{1-2x} \right)\)

Por el teorema binomial generalizado, sabemos:

• El coeficiente de\(x^n\) in\(\dfrac{1}{1 + x} = (1 + x)^{−1}\) es

\(\binom{-1}{n} = (-1)^n \binom{1 + n -1}{n} = (-1)^n \binom{n}{n} = (-1)^n \)

• El coeficiente de\(x^n\) in\(\dfrac{1}{1 − 2x} = (1 − 2x)^{−1}\) es

\(\binom{-1}{n} (-2)^n = (-1)^n \binom{1 + n -1}{n} (-2)^n = (-1)^{2n} \binom{n}{n} 2^n = 2^n \)

Por lo tanto\(c_n\), el coeficiente de\(x^n\) in\(C(x)\), es\(\dfrac{4}{3} (−1)^n + \dfrac{2}{3} · 2^n\).

3) Dejar\(E(x) = \sum_{n=0}^{\infty} e_nx^n\) ser la función generadora de\(\{e_n\}\). Entonces

\(\begin{equation} \begin{split} E(x) &= e_0 &+ e_1x &+ e_2x^2 &+ e_3x^3 &+ e_4x^4 &+ ... \\ xE(x) &= &+ e_0x &+ e_1x^2 &+ e_2x^3 &+ e_3x^4 &+ ... \\ \dfrac{1}{1-x} &= 1&+ x&+ x^2 &+ x^3 &+ x^4 &+ ... \\ \end{split} \end{equation}\)

por lo

\( \begin{equation} \begin{split} (1 − 3x)E(x) + \dfrac{2}{1-x} &= E(x) − 3xE(x) + 2 · \dfrac{1}{1-x}\\ &= (e_0 + 2) + \sum_{n=2}^{\infty} (e_n − 3e_{n−1} + 2)x^n\\ &= (e_0 + 2), \end{split} \end{equation} \)

ya que (por la relación de recurrencia) tenemos\(e_n − 3e_{n−1} + 2 = 0\) para\(n ≥ 1\). Por lo tanto

\(E(x) = \dfrac{(e_0 + 2) − \dfrac{2}{1-x}}{1 − 3x} = \dfrac{(e_0 + 2)(1 − x) − 2}{(1 − 3x)(1 − x)} \)

Ya que\(e_0 = 2\), esto significa

\(E(x) = \dfrac{(2 + 2)(1 − x) − 2}{(1 − 3x)(1 − x)} = \dfrac{2-4x}{(1 − 3x)(1 − x)} \).

Ahora usamos fracciones parciales. Escribir

\( \dfrac{2-4x}{(1 - 3x)(1 − x)} = \dfrac{A}{1-3x} + \dfrac{B}{1 − x} = \dfrac{A(1 − x) + B(1 − 3x)}{(1 − 3x)(1 − x)} = \dfrac{(A + B) − (A + 3B)x}{(1 − 3x)(1 − x)} \)

Al igualar los coeficientes en los numeradores se obtienen las ecuaciones

\(2 = A + B,\;\;\;\; −4 = −(A + 3B)\)

Sumando las dos ecuaciones nos dice eso\(2 − 4 = (A + B) − (A + 3B) = −2B\), entonces\(B = 1\). Entonces la primera ecuación nos dice eso\(A = 2 − B = 2 − 1 = 1\). Entonces

\(E(x) = \dfrac{2-4x}{(1 - 3x)(1 − x)} = \dfrac{A}{1-3x} + \dfrac{B}{1 − x} = \dfrac{1}{1-3x} + \dfrac{1}{1-x} \)

A partir del teorema binomial generalizado, sabemos que el coeficiente de\(x^n\) in\(\dfrac{1}{1 − 3x}\) es\(3n\), y el coeficiente de\(x^n\) in\(\dfrac{1}{1 − x}\) es\(1\). Por lo tanto\(e_n\), el coeficiente de\(x^n\) in\(E(x)\), es\(3^n + 1\).

Soluciones al Ejercicio 9.1.1

2) Para probar la Proposición 9.1.1 se requiere una fuerte inducción, ya que la relación recursiva convoca a dos términos anteriores. Por lo tanto, se requieren dos casos base.

3) La fórmula de la Proposición 9.1.1 da

\( \begin{equation} \begin{split} D_5 &= 5! \left( \dfrac{(-1)^0}{0!} +\dfrac{(-1)^1}{1!} + \dfrac{(-1)^2}{2!} + \dfrac{(-1)^3}{3!} + \dfrac{(-1)^4}{4!} + \dfrac{(-1)^5}{5!} \right) \\ &= 120 \left( 1 − 1 + \dfrac{1}{2} − \dfrac{1}{6} + \dfrac{1}{24} − \dfrac{1}{120} \right) \\ &= 60 − 20 + 5 − 1 = 44. \end{split} \end{equation} \)

4) Las condiciones iniciales son\(D_1 = 0\) y\(D_2 = 1\). La relación recursiva\(D_n = (n − 1)(D_{n−1} + D_{n−2})\) para\(n ≥ 3\) da\(D_3 = 2(D_2 + D_1) = 2(1 + 0) = 2\).

Ahora

\(D_4 = 3(D_3 + D_2) = 3(2 + 1) = 9,\)

y

\(D_5 = 4(D_4 + D_3) = 4(9 + 2) = 4(11) = 44.\)

Soluciones al Ejercicio 9.2.1

1) PRUEBA. Caso base:\(n = 0\). Tenemos\(c_0 = 1\) (por definición) y\(1 > 0\), entonces\(c_0 > 0\).

Paso inductivo: Comenzamos con la hipótesis inductiva. Requerremos una fuerte inducción. Seamos arbitrarios, y supongamos que la desigualdad\(k ≥ 0\) se sostiene para cada uno\(j\) con\(0 ≤ j ≤ k\); es decir, supongamos que para cada uno de tales\(j\),\(c_j > 0\).

Ahora queremos deducir eso\(c_{k+1} > 0\). Usando la relación recursiva, tenemos

\(c_{k+1} = \sum_{i=0}^{k} c_ic_{(k+1)−i−1} = \sum_{i=0}^{k} c_ic_{k-i}\)

Usando la hipótesis inductiva, tenemos\(c_j > 0\) para cada\(j\) tal que\(0 ≤ j ≤ k\). Armando estos da que\(c_{k+1}\) es una suma de\(k + 1\) términos donde cada término tiene la forma\(c_ic_{k−i}\) con\(0 ≤ i ≤ k\). Ya que\(0 ≤ k − i ≤ k\), vemos eso\(c_i > 0\) y\(c_{k−i} > 0\) así eso\(c_ic_{k−i} > 0\). De ahí

\(c_{k+1} = \sum_{i=0}^{k} c_ic_{k-i} > 0\)

Esto completa la prueba del paso inductivo.

Por el Principio de Inducción Matemática,\(c_n > 0\) para cada\(n ≥ 0\).

Soluciones al Ejercicio 9.3.1

1)

\( \begin{equation} \begin{split} B_4 = \sum_{k=1}^{4} \binom{3}{k-1} B_{4−k} &= \binom{3}{0}B_3 + \binom{3}{1}B_2 + \binom{3}{2}B_1 + \binom{3}{3}B_0 \\ &= 5 + 3(2) + 3(1) + 1(1) = 15. \end{split} \end{equation} \)

3) Si\(b_i = \dfrac{(i + 1)!}{2}\) entonces la función de generación exponencial expandida para esta secuencia es

\(\sum_{i=0}^{\infty} \dfrac{b_ix^i}{i!} = \sum_{i=0}^{\infty} \dfrac{(i + 1)!x^i}{2i!} = \sum_{i=0}^{\infty} \dfrac{(i + 1)x^i}{2}. \)

Esto es

\(\dfrac{1}{2} \sum_{i=0}^{\infty} (i + 1)x^i = \dfrac{1}{2} \left( \sum_{i=0}^{\infty} (i+1)x^i \right) = \dfrac{1}{2(1-x)^2} \)

Soluciones al Ejercicio 10.1.1

1) Ya que hay\(8\) filas en un tablero de ajedrez\(17 > 2(8)\), y, el Principio de Paloma Generalizado dice que debe haber al menos\(2 + 1 = 3\) gradas que estén todas en la misma fila del tablero. Elija tal fila, y llámela Fila\(A\). Tenga en cuenta que Row\(A\) contiene como máximo\(8\) gradas.

Hay por lo menos\(17 − 8 = 9\) gradas que no están en fila\(A\). Ya que hay\(7\) otras filas en el tablero de ajedrez, y\(9 > 1(7)\), el Principio Pigeonhole dice que debe haber al menos\(1 + 1 = 2\) gradas que estén en la misma fila, de entre las otras filas del tablero. Elija tal fila, y llámela Fila\(B\). Tenga en cuenta que Row\(B\) también contiene como máximo\(8\) gradas.

Al menos queda\(17−8−8 = 1\) torre, por lo que debe haber una torre en algún lugar del tablero que no esté ni en Row\(A\) ni Row\(B\). Elige tal Torre\(1\), y llama a la fila que está en Row\(C\). Ya que hay al menos\(2\) gradas en fila\(B\), al menos una de ellas no debe estar en la misma columna que Torre\(1\). Elige una grada así, Torre\(2\). Ya que hay al menos\(3\) gradas en Row\(A\), al menos una de ellas no debe estar en la misma columna que ni Rook\(1\) ni Rook\(2\). Elige tal Torre, y llámela Torre\(3\). Ahora Torres,\(1\)\(2\), y\(3\) no se amenazan entre sí, así que cumplan con los requisitos del problema.

3) Utilizamos el principio de encasillamiento aún más generalizado con\(n − 1 = 15\) para los adultos, y\(n_2 = 23\) para los niños (y\(m = 2\) categorías: adultos y niños). El principio nos dice que mientras al menos

\(n_1 + n_2 − m + 1 = 15 + 23 − 2 + 1 = 37\)

se acercan a la gente, tendrá suficiente gente para llevar su arte en el desfile.

Soluciones al Ejercicio 10.2.2

2) De las piezas básicas de información que necesitamos para completar un diagrama de Venn, no se nos ha dado una: la cantidad de aplicaciones de Kevin que son gratuitas y requieren acceso a internet. Afortunadamente, podemos usar inclusión-exclusión para resolver esto a partir de los demás. Usamos\(F\) para representar el conjunto de aplicaciones gratuitas;\(G\) para representar los juegos y\(I\) para representar las aplicaciones que requieren Internet. Entonces nos han dicho:

\(|F| = 78, |I| = 124, |G| = 101, |F ∩ G| = 58, |G ∩ I| = 62, |F ∩ G ∩ I| = 48, |F ∪ G ∪ I| = 165.\)

Usando inclusión-exclusión, tenemos

\(165 = 78 + 124 + 101 − 58 − 62 − |F ∩ I| + 48\),

por lo

\(|F ∩ I| = 78 + 124 + 101 − 58 − 62 + 48 − 165 = 66\).

El valor que nos han pedido es

\(|F ∩ I ∩ \overline{G}| = |F ∩ I| − |F ∩ I ∩ G| = 66 − 48 = 18\).

3) El número de enteros entre\(1\) y\(60\) que son divisibles por\(2\) es\(\dfrac{60}{2} = 30\). Llama al conjunto de estos enteros\(A\). El número de enteros entre\(1\) y\(60\) que son divisibles por\(3\) es\(\dfrac{60}{3} = 20\). Llama al conjunto de estos enteros\(B\). El número de enteros entre\(1\) y\(60\) que es divisible por\(5\) is\(\dfrac{60}{5} = 12\). Llama al conjunto de estos enteros\(C\). Entonces\(|A ∩ B|\) es el número de enteros entre\(1\) y\(60\) que son divisibles por\(2\) y\(3\); es decir, el número que son divisibles por\(6\). Esto es\(\dfrac{60}{6} = 10\). Del mismo modo,\(|A ∩ C|\) es el número de enteros entre\(1\) y\(60\) que son divisibles por\(2\) y\(5\); es decir, el número que son divisibles por\(10\). Esto es\(\dfrac{60}{10} = 6\). También,\(|B ∩ C|\) es el número de enteros entre\(1\) y\(60\) que son divisibles por\(3\) y\(5\); es decir, el número que son divisibles por\(15\). Esto es\(\dfrac{60}{15} = 4\). Finalmente,\(|A ∩ B ∩ C|\) es el número de enteros entre\(1\) y\(60\) que son divisibles por\(2\),\(3\), y\(5\); es decir, el número que son divisibles por\(30\). Esto es\(\dfrac{60}{30} = 2\).

Nos han pedido\(|A ∪ B ∪ C|\). Usando inclusión-exclusión, vemos que la respuesta es\(30 + 20 + 12 − 10 − 6 − 4 + 2 = 44\).

Soluciones al Ejercicio 11.2.1

1) a) El único incidente de borde con\(a\) es\(e_1\), por lo que la valencia de\(a\) es\(1\).

b) El único incidente de borde con\(b\) es\(e_2\), por lo que la valencia de\(b\) es\(1\).

c) Los bordes incidentes con\(c\) son\(e_1\)\(e_3\),, y\(e_4\), así la valencia de\(c\) es\(3\).

d) Los bordes incidentes con\(d\) son\(e_2\)\(e_3\),, y\(e_5\), así la valencia de\(d\) es\(3\).

e) Los bordes incidentes con\(e\) son\(e_4\)\(e_5\),, y\(e_6\), entonces la valencia de\(e\) es\(3\).

Ya que\(e_6 = \{e, e\}\) es un bucle, la gráfica no es sencilla. No hay vértice aislado, porque ningún vértice tiene valencia\(0\). El único vecino de\(a\) es\(c\), y el único incidente de borde con\(a\) es\(e_1\).

3) a) Los bordes incidentes con\(a\) son\(e_1\) y\(e_2\), por lo que la valencia de\(a\) es\(2\).

b) Los bordes incidentes con\(b\) son\(e_1\) y\(e_3\), por lo que la valencia de\(b\) es\(2\).

c) Los bordes incidentes con\(c\) son\(e_2\) y\(e_3\), por lo que la valencia de\(c\) es\(2\).

d) No hay bordes incidentes con\(d\), por lo que la valencia de\(d\) es\(0\).

No hay bucles ni múltiples aristas, por lo que la gráfica es simple. La gráfica sí tiene un vértice aislado, es decir,\(d\) (porque la valencia de\(d\) es\(0\)). Los vecinos de\(a\) son\(b\) y\(c\), y los bordes incidentes con\(a\) son\(e_1\) y\(e_2\), como ya se mencionó anteriormente.

Soluciones al Ejercicio 11.3.1.

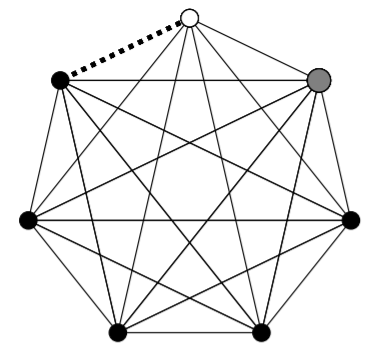
3) En la siguiente imagen, la línea punteada representa el borde que eliminaremos. Si entonces eliminamos el vértice blanco, la gráfica que queda está completa. Si en cambio entonces eliminamos el vértice gris grande (que es el siguiente en el sentido de las agujas del reloj desde el vértice blanco), la gráfica restante no estará completa, ya que el vértice blanco sólo es adyacente a cuatro de los cinco vértices negros.

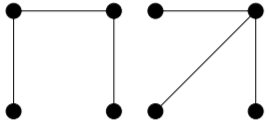
4) PRUEBA. Dejar\(G\) ser una gráfica con e bordes.

Caso base:\(e = 0\). Ya que no\(G\) tiene bordes, cada vértice tiene valencia\(0\). Entonces el número de vértices de valencia impar es\(0\), que es par.

Paso inductivo: Comenzamos con la hipótesis inductiva. Fijar\(e ≥ 0\), y asumir que cada gráfica con bordes e tiene un número par de vértices de valencia impar.

Ahora queremos deducir que cada gráfica con\(e + 1\) aristas tiene un número par de vértices de valencia impar. Dejar\(H\) ser una gráfica arbitraria con\(e+ 1\) aristas. Elija un borde\(f\) (hay uno desde\(e + 1 ≥ 1\)), y llame a sus extremos\(u\) y\(v\). Vamos\(H' = H \setminus \{f\}\).

Observe que\(H'\) tiene\(e + 1 − 1 = e\) bordes, por lo que nuestra hipótesis de inducción se aplica a\(H'\). Por lo tanto,\(H'\) tiene un número par de vértices de valencia impar. Llama a este número\(2m\), donde\(m ∈ \mathbb{Z}\).

Observe que la valencia de cada vértice de\(H\) es la misma que su valencia en\(H'\) si el vértice no es\(u\) o\(v\), y es uno mayor que su valencia en\(H'\) si el vértice es cualquiera\(u\) o\(v\). Considere los tres casos posibles:\(u\) y\(v\) ambos tienen valencia par en\(H'\);\(u\) y\(v\) ambos tienen valencia impar en\(H'\); o exactamente uno de\(u\) y\(v\) tiene valencia par en\(H'\).

Si\(u\) y\(v\) ambos tienen valencia par en\(H'\), entonces ambos tienen valencia impar en\(H\), por lo que el número de vértices de valencia impar en\(H\) debe ser\(2m + 2\), que es par.

Si\(u\) y\(v\) ambos tienen valencia impar en\(H'\), entonces ambos tienen valencia par en\(H\), por lo que el número de vértices de valencia impar en\(H\) debe ser\(2m − 2\), que es par.

Si exactamente uno de\(u\) y\(v\) tiene incluso valencia en\(H'\), entonces exactamente uno de\(u\) y\(v\) tendrá incluso valencia en\(H\) (el otro, ya que la valencia de cada uno de\(u\) y\(v\) sube por\(1\)). Entonces el número de vértices de valencia impar en\(H\) debe ser\(2m\) (aunque uno de los vértices específicos de valencia impar haya cambiado entre\(u\) y\(v\)), que es par.

En todos los casos,\(H\) tiene un número par de vértices de valencia impar. Esto completa la prueba del paso inductivo.

Por el Principio de Inducción Matemática, cada gráfica con al menos\(0\) aristas tiene un número par de vértices de valencia impar.

Soluciones al Ejercicio 11.4.1

1) Las gráficas no son isomórficas, porque el único vértice de valencia\(1\) en\(G\) (es decir,\(c\)) es adyacente a un vértice de valencia\(3\) (es decir\(d\)), pero el único vértice de valencia\(1\) en\(H\) (es decir,\(z\)) es adyacente solo a un vértice de valencia \(1\)(a saber,\(y\)).

Aquí hay una prueba más completa. Supongamos que\(\varphi: G → H\) es un isomorfismo. (Esto conducirá a una contradicción.) Debemos tener

\(d_H \left( \varphi(c) \right) = d_G(c) = 1\).

(Este principio fue señalado en la prueba de la Proposición 11.4.1 (3).) El único vértice de valencia\(1\) en\(H\) es\(z\), por lo que esto implica que\(\varphi(c) = z\).

Ahora, ya que\(d ∼ c\), debemos tener\(\varphi(d) ∼ \varphi(c)\). Ya que\(\varphi(c) = z\), y el único vecino de\(z\) es\(y\), esto implica\(\varphi(d) = y\). Entonces

\(d_H(y) = \left( d_H \varphi(d) \right) = d_G(d)\).

Sin embargo,\(d_H(y) = 2\) y\(d_G(d) = 3\), entonces\(d_H(y) 6= d_G(d)\). Esto es una contradicción.

3) No hay vértice de valencia\(0\) en\(G_1\), sino\(A\) que es un vértice de valencia\(0\) en\(G_2\). Por lo tanto\(G_1\) y\(G_2\) no tienen la misma secuencia de grado, por lo que no son isomórficas.

Soluciones al Ejercicio 11.4.2

2) De las cinco etiquetas de vértice, podemos elegir cualquiera de dos para unir con un borde. Así, el número de gráficas etiquetadas en cinco vértices con un borde es\(\binom{5}{2} = 10\).

3) Observe que hay aristas\(\binom{5}{2} = 10\) totales posibles en una gráfica sobre\(5\) vértices. Así, el número de gráficas etiquetadas en\(5\) vértices con\(3\) aristas es el número de formas de elegir\(3\) de estas aristas\(10\) etiquetadas. Entonces hay gráficas\(\binom{10}{3} = 120\) etiquetadas en\(5\) vértices que tienen\(3\) borde.

De igual manera, hay gráficas\(\binom{10}{4} = 210\) etiquetadas en\(5\) vértices que tienen\(4\) aristas. Así, en total hay gráficas\(120 + 210 = 330\) etiquetadas en\(5\) vértices que tienen\(3\) o\(4\) aristas.

Soluciones al Ejercicio 12.1.1

1) PRUEBA. Demostramos, por inducción en\(n\), que si\(n ≥ 1\), y\(G\) es cualquier dígrafo con\(n\) vértices que no tiene bucles o multiarcos, entonces

\(|A(G)| = \sum_{v∈V (G)} d_G^+ (v) = \sum_{v∈V (G)} d_G^-(v) \)

Caso base:\(n = 1\). Dejar\(G\) ser un dígrafo sin bucles ni multiarcos, y con un solo vértice\(v_1\). Entonces no hay arcos en\(G\), entonces\(|A(G)| = 0 = d_G^+ (v_1) = d_G^- (v_1)\). Entonces la conclusión deseada es cierta cuando\(n = 1\).

Ahora establecemos el paso de inducción. Supongamos que\(n ≥ 1\), la fórmula se mantiene para cada dígrafo con\(n\) vértices que no tiene bucles o multiarcos, y\(G\) es un dígrafo con\(n + 1\) vértices que no tiene bucles o multiarcos.

Elija un vértice arbitrario\(u\) de\(G\). Let

• \(N^+\)ser el conjunto de vecinos externos de\(u\), y\(N^−\) el conjunto de invecinos de\(u\),
• \(s = |N +| = d + G (u)\)ser el número de arcos que comienzan en\(u\),
• \(t = |N −| = d − G (u)\)ser el número de arcos que terminan en\(u\), y
• \(G'\)ser el dígrafo obtenido\(G\) mediante la eliminación\(u\) y sus arcos\(s + t\) incidentes.

Tenga en cuenta que:

• \(V (G') = V (G) \setminus {u}\), así lo\(G'\) ha hecho\(n\) los vértices.
• \(|A(G')| = |A(G)| − s − t\).
• Porque\(v ∈ V (G') \setminus N^−\), tenemos\(d_{G'}^+(v) = d_G^+ (v)\) (porque los vecinos externos de\(v\) adentro\(G'\) son exactamente los mismos que los outneighbours de\(v\) in\(G\)).
• Porque\(v ∈ N^−\), tenemos\(d_G^+ (v) = d_G^+ (v)−1\) (porque\(u\) se cuenta como un vecino externo de\(v\) adentro\(G\), pero no está en\(G'\) así que no se puede contar como un vecino externo en\(G'\)).
• Declaraciones similares sostienen con\(N^−\) reemplazado por\(N^+\).

De ahí

\( \begin{equation} \begin{split} \sum_{v∈V (G)} d_G^+(v) &= \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_G^+(v) + \sum_{v∈N^−} d_G^+(v) + \sum_{v∈\{u\}} d_G^+(v) \\[0.125in] &= \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_{G'}^+(v) + \sum_{v∈N^−} \left( d_{G'}^+(v) +1 \right) + d_{G'}^+(u) \\[0.125in] &= \left( \sum_{v∈V (G) \setminus (N^−∪\{u\})} d_{G'}^+(v) + \sum_{v∈N^−} d_{G'}^+(v) \right) + |N^−| + d_{G'}^+(u)\\[0.125in] &= \sum_{v∈V (G')} d_{G'}^+(v) + t + s\\[0.125in] &= |A(G')| + s + t \;\;\;\;\;(\text{induction hypothesis}) \\[0.125in] &= |A(G)|. \end{split} \end{equation} \)

De igual manera, podemos argumentar eso\(\sum_{v∈V (G)} d^−G(v) = |A(G)|\). Esto completa el paso inductivo y la prueba.

3) Comenzando en la parte superior y trabajando en el sentido de las agujas del reloj, etiquetar los vértices del dígrafo\(a\)\(b\)\(c\),\(d\),, y\(e\). Entonces:

• \(a\)tiene outvalencia\(2\) e invalencia\(1\);
• \(b\)tiene outvalencia\(2\) e invalencia\(2\);
• \(c\)tiene outvalencia\(1\) e invalencia\(2\);
• \(d\)tiene outvalencia\(2\) e invalencia\(2\);
• \(e\)tiene outvalencia\(1\) e invalencia\(1\).

Soluciones al Ejercicio 12.2.1

2) Esta gráfica está conectada. Para ver esto, tenga en cuenta que\((a, j, g, v, e, d, i, h, c, b)\) es un paseo que pasa por todos los vértices de\(G\), por lo que es posible caminar de\(a\) a cualquier otro vértice. Por lo tanto, el componente conectado que contiene\(a\) es\(V(G) = \{a, b, c, d, e, f, g, h, i, j\}\). Hay varios paseos de longitud\(5\) desde\(a\) hasta\(f\). Un ejemplo es\((a, g, a, j, g, f)\).

3) Esta gráfica no está conectada. Para ver esto, tenga en cuenta que no hay bordes desde ningún vértice\(\{a, d, e, f, g, j\}\) hasta ningún vértice en\(\{b, c, h, i\}\). De hecho el componente conectado que contiene\(a\) es\(\{a, d, e, f, g, j\}\). (El paseo\((a, d, e, f, g, j)\) pasa por todos estos vértices, pero ninguno de estos vértices es adyacente a ningún vértice que no esté en el subconjunto). Hay varios paseos de longitud\(3\) desde\(a\) hasta\(d\). Un ejemplo es\((a, d, a, d)\).

Soluciones al Ejercicio 12.3.1

1) (a) Hay muchos caminos de longitud\(3\). Un ejemplo es\((a, b, c, h)\).

b)\((b, c, f, b)\) es un ciclo de duración\(3\).

c) no\((a, b, c, b)\) es ni un camino ni un ciclo. No es un camino porque los vértices no son todos distintos. (Es decir, el vértice\(b\) ocurre dos veces.) No es un ciclo, porque el primer vértice (es decir,\(a\)) no es lo mismo que el vértice final (es decir,\(b\)).

3) PRUEBA. Dejar\((u = u_1, u_2, . . . , v = u_k, u)\) ser un ciclo de\(G\) en el que\(u\) y\(v\) aparecen como vértices consecutivos. Vamos\(G' = G \setminus \{uv\}\).

Dejar\(x\) y\(y\) ser vértices arbitrarios de\(G\). Ya que\(G\) está conectado, hay un paseo\((x = x_1, x_2, . . . , x_m = y)\) de\(x\) a\(y\) adentro\(G\). Si este paseo no contiene el borde\(uv\) entonces también es un paseo por dentro\(G'\). Si sí contiene el borde\(uv\), entonces podemos encontrar algunos\(i\) con\(1 ≤ i ≤ m − 1\) tal que o bien\(x_i = u\) y\(x_{i+1} = v\), o viceversa. Por cada tal\(i\), reemplace el par\((x_i , x_{i+1})\) en la caminata por cualquiera\((u = u_1, u_2, . . . , v = u_k)\) o\((v = u_k, u_{k−1}, . . . , u = u_1)\) (según corresponda, dependiendo de si\(x_i = u\) o\(x_i = v\)). El resultado es un paseo de\(x\) a\(y\) que no usa el borde\(uv\), así está en\(G'\). Desde\(x\) y\(y\) fueron arbitrarios vértices de\(G'\), para cualesquiera dos vértices\(x\) y\(y\) de\(G'\) hay un\(x − y\) paseo, así por definición,\(G\) está conectado.

Soluciones al Ejercicio 12.4.1

1) PRUEBA. Deja\(T\) ser un árbol, y deja\(v\) ser una hoja de\(T\). Considerar\(T \setminus \{v\}\). Ciertamente no puede tener ningún ciclo, ya que no\(T\) tiene ciclos. Dejar\(x\) y\(y\) ser vértices arbitrarios de\(T \setminus \{v\}\). Ya que\(T\) está conectado, hay un\(x − y\) paseo adentro\(T\), así que por la Proposición 12.3.1, hay un\(x − y\) camino en\(T\). Ya que\(v\) es una hoja de\(T\), si un\(x − y\) paseo usa el vértice\(v\) entonces el vecino de\(v\) tendría que venir tanto antes como después\(v\) en el paseo, ya que\(v\) tiene un solo vecino, por lo que tal caminata no sería un camino. Así, el\(x − y\) camino no puede usar el vértice\(v\), por lo que sigue siendo un camino en\(T \setminus \{v\}\). Desde\(x\) y\(y\) fueron vértices arbitrarios, esto demuestra que\(T \setminus \{v\}\) está conectado. Esto completa la prueba.

3) Los dos árboles no isomórficos no etiquetados en\(4\) vértices son:

Soluciones al Ejercicio 13.1.1

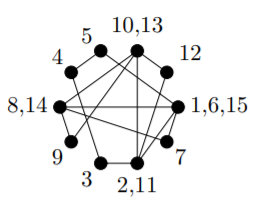
1) Esta gráfica tiene recorridos de Euler, porque está conectada y todos los vértices tienen incluso valencia. Una gira de Euler es\((d, f, g, j, a, d, e, i, h, b, f, c, b, i, d)\). En la siguiente figura se indican los vértices\(1, 2, 3, . . .\) en el orden en que se visitan.

Soluciones al Ejercicio 13.2.1

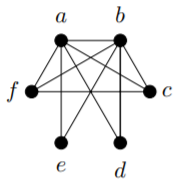
2) a) En el cierre, podemos unirnos\(a\) a\(b\); podemos unirnos\(a\) a\(c\); y podemos unirnos\(b\) a\(f\). Esto completa el cierre, que se muestra a continuación. No es fácil ver a partir de esto si la gráfica tiene o no un ciclo Hamilton. De hecho, no lo hace.

b) El cierre de esta gráfica es\(K_6\). Podemos ver fácilmente a partir de esto que la gráfica sí tiene un ciclo Hamilton. (Para ver que el cierre es\(K_6\), observe que cada vértice de la gráfica tiene valencia al menos\(2\). Así, los dos vértices de valencia se\(4\) pueden unir a cada uno de sus no vecinos. Después de hacerlo, cada vértice tiene valencia al menos\(3\), por lo que cada vértice se puede unir a cada otro vértice.)

3) Dejar\(G\) ser la gráfica que se ha mostrado aquí. Usando la notación del Teorema 13.2.1, let\(S = \{a, f\}\). Entonces\(|S| = 2\), pero\(G \setminus S\) tiene componentes\(3\) conectados:\(\{b, e\}\),\(\{c, h\}\), y\(\{d, g\}\). Ya que\(3 > 2\),\(G\) no puede tener un ciclo Hamilton.

Soluciones al Ejercicio 14.1.1

1) PRUEBA. Los árboles son bipartitos (no tienen ningún ciclo en absoluto, así que ciertamente no tienen ningún ciclo de longitud impar), así que el Teorema 14.1.3 nos dice que son de clase uno.

2) PRUEBA. La prueba es por contradicción: supongamos que\(n\) es impar, y el ciclo

\(C_n = (v_0, v_1, . . . , v_n = v_0)\)

es la clase uno. Dado que cada vértice de\(C_n\) tiene valencia dos, esto significa que la gráfica tiene una coloración de bordes adecuada que usa solo\(2\) colores. Llamemos a los colores rojo y azul.

Supongamos, sin pérdida de generalidad, que el borde\(v_0v_1\) es rojo. El borde\(v_1v_2\) no puede ser del mismo color que\(v_0v_1\) (porque ambos son incidentes con\(v_1\)), por lo que\(v_1v_2\) debe ser azul. El borde\(v_2v_3\) no puede ser del mismo color que\(v_1v_2\) (porque ambos son incidentes con\(v_2\)), por lo que\(v_2v_3\) debe ser rojo. Continuando de esta manera, vemos (por inducción encendido\(k\)) que\(v_kv_{k+1}\) es rojo cada vez que\(k\) es par, y es azul siempre que\(k\) es extraño. (Es decir, los dos colores deben alternar rojo, azul, rojo, azul, rojo, azul,.. a medida que vamos dando la vuelta al ciclo.)

En particular, como\(n\) es extraño, sabemos que\(n − 1\) es par, por lo que esto significa que el borde\(v_{n−1}v_n\) es rojo. No obstante, tenemos\(v_n = v_0\) así los bordes\(v_{n−1}v_n\) y ambos\(v_0v_1\) son incidentes con el vértice\(v_0\)), por lo que no pueden ser del mismo color. El contradice el hecho de que ambos bordes son rojos.

Soluciones al Ejercicio 14.2.1

1) La siguiente\(2\) coloración de los bordes de no\(K_6\) tiene triángulo sólido ni punteado\(K_4\) (porque se forman los bordes sólidos\(K_{3,3}\), que no tiene ciclos de longitud impar, y cada componente conectado del gráfico punteado es solo\(K_3\)):

3) PRUEBA. Demostramos esto por inducción en\(k + \ell\). El caso base es cuando\(k + \ell = 2\) (así\(k = \ell = 1\)). Entonces

\(R(k, \ell) = R(1, 1) = 1 < 4 = 2^{1+1} = 2^{k+ \ell} \).

Entonces la desigualdad es válida en el caso base.

Para el paso de inducción, asuma\(k + \ell ≥ 2\), y eso\(R(k' , \ell ' ) ≤ 2 k' + \ell '\), cuando sea\(k' + \ell ' < k + \ell\). Ya que\(R(k, \ell) = R(\ell, k)\), podemos asumir\(k ≤ \ell\) (intercambiando\(k\) y\(\ell\), si es necesario). Si\(k = 1\), entonces

\(R(k, \ell) = R(1, \ell) = 1 = 2^0 < 2^{k + \ell} .\)

Por lo tanto, podemos asumir\(2 ≤ k ≤ \ell\). Desde\((k − 1) + \ell < k + \ell\) y\(k + (\ell − 1) < k + \ell\), la hipótesis de inducción nos dice que

\(R(k − 1, \ell) ≤ 2^{(k−1) + \ell} \text{ and } R(k, \ell − 1) ≤ 2^{k+(\ell−1)} \).

Por lo tanto

\(\begin{equation} \begin{split} R(k, \ell) &≤ R(k − 1, \ell) + R(k, \ell − 1) \\ &≤ 2^{(k−1)+\ell} + 2^{k+(\ell−1)} \\ &= 2^{k+\ell−1} + 2^{k+\ell−1} \\ &= 2 · 2^{k+\ell−1} \\ &= 2^{k+\ell}. \end{split} \end{equation}\)

Esto completa la prueba.

4) Desde\(R(k, \ell) ≤ R(k' , \ell ')\) cuando\(k ≤ k'\) y\(\ell ≤ \ell '\), tenemos

\(40 ≤ R(3, 10) ≤ R(3, 11)\).

Además, desde\(R(k, \ell) ≤ R(k − 1, \ell) + R(k, \ell − 1)\) y\(R(2, \ell) = \ell\), tenemos

\(R(3, 11) ≤ R(3 − 1, 11) + R(3, 11 − 1) = R(2, 11) + R(3, 10) ≤ 11 + 42 = 53\).

Entonces\(40 ≤ R(3, 11) ≤ 53\).

Soluciones al Ejercicio 14.2.2

2) PRUEBA. Eso lo asumimos\(N − 1 > (c + 1)(n − 1)\). Considera una coloración arbitraria de los bordes de\(K_N\) con\(c + 1\) colores. Fijar un vértice\(v\). Dado que\(v\) tiene bordes\(N − 1 > (n − 1)(c + 1)\) incidentes, el principio de encasillamiento generalizado nos dice que debe haber algún conjunto de al menos\(n\) bordes incidentes con los\(v\) que todos estén coloreados con el mismo color, digamos color\(i\). Observe el subgrafo inducido de\(K_N\) en los\(n\) otros puntos finales de estos bordes. Si algún borde\(xy\) de esta subgrafía inducida está coloreado con color\(i\), entonces todos los bordes del triángulo\(\{v, x, y\}\) han sido coloreados con color\(i\), también lo\(K_N\) ha hecho un triángulo monocromático.

Si por otro lado ningún borde de la subgrafía inducida ha sido coloreado con color\(i\), entonces el subgráfico inducido es una\(K_n\) cuyos bordes han sido coloreados con los\(c\) colores restantes. Por hipótesis, cada coloración tiene un triángulo monocromático. Esto completa la prueba.

Soluciones al Ejercicio 14.2.3

1) Buscamos el valor más pequeño de\(n\) tal manera que cada coloración de bordes\(K_n\) con líneas punteadas, discontinuas y continuas tenga un triángulo punteado\(K_2\), punteado\(K_2\) o sólido. La siguiente coloración muestra que\(R(2, 2, 3) > 2\):

Sin embargo,\(R(2, 2, 3) = 3\). Esto se debe a que si alguna arista está punteada o discontinua, entonces hay un punteado o punteado\(K_2\); si no hay bordes punteados o punteados, entonces cada borde es sólido, entonces hay un sólido\(K_3\).

2) Eso lo demostraremos\(R(2, 4) = 4\). Buscamos el valor más pequeño de\(n\) tal manera que cada coloración de bordes\(K_n\) con líneas discontinuas o continuas tenga un punteado\(K_2\) o un sólido\(K_4\). El siguiente color demuestra que\(R(2, 4) > 3\);

Sin embargo, en\(K_4\) si algún borde está discontinuo, entonces hay un punteado\(K_2\), mientras que si no hay bordes discontinuos, entonces hay un sólido\(K_4\).

Soluciones al Ejercicio 14.3.1

2) PRUEBA. Procederemos por inducción en\(n\).

Caso base:\(n = 1\). Entonces\(K_1\) está la gráfica con un vértice y sin aristas, y\(χ(K_1) = 1\). Así, cuando\(n = 1\) tenemos\(χ(K_n) = n\).

Paso de inducción: Comenzamos con la hipótesis de inducción. \(k ≥ 1\)Sea arbitrario, y supongamos que\(χ(K_k) = k\), para que podamos colorear correctamente\(K_k\) usando\(k\) colores, y se requieren\(k\) colores para hacerlo.

Ahora considere la gráfica\(K_{k+1}\). Dejar\(v\) ser un vértice arbitrario de esta gráfica. Por nuestra hipótesis de inducción,\(χ(K_{k+1} \setminus \{v\}) = k\). Por lo tanto, cualquier coloración adecuada de\(K_{k+1}\) debe utilizar al menos\(k\) colores en los vértices que no sean\(v\). No es posible colorear\(v\) con ninguno de estos\(k\) colores, ya que\(v\) es adyacente a todos los demás vértices, por lo que tiene un vecino que se colorea con cada uno de estos\(k\) colores. Por lo tanto,\(χ(K_{k+1}) ≥ k + 1\). De hecho, dado que\(v\) es el único vértice aún no coloreado por estos\(k\) colores, está claro que los\(k + 1\) colores bastan para colorear la gráfica: coloreamos\(v\) con un nuevo color, que es el\(k + 1^{\text{st}}\) color. Esto sin duda será una coloración adecuada de\(K_{k+1}\). Así,\(χ(K_{k+1}) = k + 1\), completando la etapa de inducción.

Por el Principio de Inducción Matemática,\(χ(K_n) = n\) para cada\(n ≥ 1\).

4) El hecho de que\(G\) contenga una subgrafía isomórfica a\(K_i\) implica que\(χ(G) ≥ i\). El hecho de que\(∆(G) ≤ j\) implica que

\(χ(G) ≤ ∆(G) + 1 ≤ j + 1\).

Entonces,\(4 ≤ i ≤ χ(G) ≤ j + 1 ≤ 7\).

Si también sabemos que\(G\) está conectado y no es ni una gráfica completa ni un ciclo de longitud impar, entonces\(χ(G) ≤ ∆(G) ≤ j\), así\(4 ≤ i ≤ χ(G) ≤ j ≤ 6\) en este caso.

Soluciones al Ejercicio 15.1.1

1) PRUEBA. Dejar\(G\) ser una gráfica con una subgrafía no plana\(H\). Supongamos (hacia una contradicción) que\(G\) es plano. Encuentre una incrustación plana de\(G\), y elimine vértices y/o aristas (según corresponda) para llegar al subgrafo\(H\). Ninguna arista que no comparta un vértice final tiene puntos en común en la incrustación de\(G\), y las aristas que comparten un vértice final no tienen otros puntos en común. Esta propiedad no se cambia eliminando vértices y/o aristas, por lo que nuestro resultado es una incrustación plana de\(H\). Pero esto es imposible, ya que\(H\) es no planar. La contradicción demuestra que\(G\) debe ser plano. Ya que\(K_5\) es un subgrafo de\(K_n\) para cada\(n ≥ 6\) y\(K_5\) es no planar por el Teorema 15.1.1, esto demuestra que\(K_n\) es no planar para cada\(n ≥ 6\).

3) Mostramos una incrustación plana de la gráfica, la incrustación plana con la gráfica dual mostrada en gris, y la gráfica dual.

Soluciones al Ejercicio 15.2.1

1) Demostraremos que para cualquier incrustación planar de un gráfico plano desconectado con exactamente dos componentes conectados,\(|V| − |E| + |F| = 3\).

PRUEBA. Demostraremos esta fórmula por inducción en el número de caras de la incrustación. Let\(G\) Ser una incrustación plana de una gráfica con exactamente dos componentes conectados.

Caso base: Si\(|F| = 1\) entonces\(G\) no puede tener ningún ciclo (de lo contrario el interior y el exterior del ciclo serían caras\(2\) distintas). Entonces\(G\) debe consistir en dos gráficas conectadas que no tengan ciclos, es decir, dos árboles,\(T_1\) y\(T_2\). Por Teorema 12.4.1 sabemos que debemos tener\(|E(T_1)| = |V (T_1)| − 1\) y\(E(T_2) = V (T_2) − 1\), así

\(V | − |E| + |F| = |V (T_1)| + |V (T_2)| − (|V (T_1)| − 1) − (|V (T_2) − 1) + 1 = 3\).

Paso inductivo: Comenzamos por exponer nuestra hipótesis inductiva. \(k ≥ 1\)Sea arbitrario, y supongamos que para cualquier incrustación plana de una gráfica que tenga exactamente dos componentes conectados, tal que la incrustación tenga\(k\) caras,\(|V| − |E| + |F| = 3\).

Let\(G\) Ser una incrustación plana de una gráfica que tiene exactamente dos componentes conectados, de tal manera que el componente tiene\(k + 1 ≥ 2\) caras. Dado que los bosques tienen una sola cara,\(G\) deben tener un ciclo en al menos uno de sus componentes. Elija cualquier borde\(e\) que esté en un ciclo de\(G\), y deje\(H = G \setminus \{e\}\). Claramente, tenemos

\(|E(H)| = |E(G)| − 1\)

y\(|V(H)| = |V(G)|\). También,

\(F(H)| = |F(G)| − 1 = k\)

ya que el borde\(e\) que forma parte de un ciclo debe separar dos caras de\(G\), las cuales están unidas en una cara de\(H\). Además, ya que\(e\) estaba en un ciclo y\(G\) tiene dos componentes conectados, por un argumento similar al dado en la Proposición 12.3.3\(H\) tiene dos componentes conectados, y\(H\) tiene una incrustación plana inducida por la incrustación plana de\(G\). Por lo tanto, nuestra hipótesis inductiva se aplica a\(H\), entonces

\(\begin{equation} \begin{split} 2 &= |V (H)| − |E(H)| + |F(H)| \\[0.125in] &= |V (G)| − (|E(G)| − 1) + (|F(G)| − 1) \\[0.125in] &= |V (G)| − |E(G)| + |F(G)| = 3 \end{split} \end{equation}\)

Esto completa el paso inductivo.

Por el Principio de Inducción Matemática,\(|V| − |E| + |F| = 3\) para cualquier incrustación plana de gráfica que tenga exactamente dos componentes conectados.

4) El valor para\(|V | − |E| + |F|\) en un toro es\(0\). Por ejemplo, considere la gráfica sobre\(5\) vértices que consta de dos ciclos de longitud\(3\) que se encuentran en un vértice. Dibuja esta gráfica sobre un toro para que un ciclo pase por el agujero en el medio, y un ciclo vaya alrededor del borde exterior del toro. Esta incrustación tiene una cara, ya que el primer ciclo corta el toro en algo parecido a un cilindro, y el segundo corta el cilindro en un rectángulo. Hay\(5\) vértices y\(6\) aristas, así\(|V| − |E| + |F| = 5 − 6 + 1 = 0\), como se reivindica.

Soluciones al Ejercicio 15.3.1

1) Primero, observe que dado que\(G\) es cúbico, cada vértice tiene valencia\(3\), lo cual es impar. Por lo tanto, por Corolario 11.3.1,\(G\) debe tener un número par de vértices. Esto significa que el número de vértices en el ciclo Hamilton, y el número de aristas en el ciclo Hamilton (que son iguales) son ambos pares. Así, podemos colorear los bordes del ciclo Hamilton con\(2\) colores, digamos azul y rojo, alternando entre los dos colores en todo el ciclo. Dado que la gráfica es cúbica, cada vértice incide ahora en exactamente un borde que aún no ha sido coloreado. Por lo tanto, podemos colorear todos los bordes restantes con un solo color — verde, digamos. Por lo tanto, tenemos correctamente\(3\) -borde coloreado\(G\). Ya que\(∆(G) = 3\), esto significa que\(G\) es una gráfica de clase uno.

2) Utilizamos las letras\(R\),\(G\),\(B\), y\(Y\) para representar los cuatro colores. A la cara exterior (que aparece gris en la imagen) se le asignará el color\(B\).

Soluciones al Ejercicio 16.1.1

1) PRUEBA. \(L\)Sea un cuadrado\(n×n\) latino cuyas entradas provengan de un conjunto\(N\) de cardinalidad\(n\), y que\(L'\) sea el resultado de intercambiar fila\(i\) con fila\(j\).

\(k ∈ \{1, . . . , n\}\)Sea arbitrario, y considere la columna\(k\) de\(L'\). Sus entradas son exactamente las mismas que las entradas de columna\(k\) de\(L\), excepto que la\(i^{\text{th}}\) entrada ha sido intercambiada con la\(j^{\text{th}}\) entrada. Dado que cada elemento de\(N\) aparece exactamente una vez en\(k\) la columna de\(L\), también aparece exactamente una vez en\(k\) la columna de\(L'\) (aunque posiblemente en una posición diferente). Dado que\(k\) era arbitrario, cada elemento de\(N\) aparece exactamente una vez en cada columna de\(L'\).

Ahora considere fila\(k\) de\(L'\). Si\(k \neq i\),\(j\), entonces esta fila es exactamente la misma que fila\(k\) de\(L\). Dado que cada elemento de\(N\) aparece exactamente una vez en fila\(k\) de\(L\), también aparece exactamente una vez (y en la misma posición incluso) en fila\(k\) de\(L'\). Si\(k = i\) o\(k = j\), entonces fila\(k\) de\(L'\) es la misma que alguna otra fila (la\(i^{\text{th}}\) fila\(j^{\text{th}}\) o, respectivamente) de\(L\). Dado que cada elemento de\(N\) aparece exactamente una vez en esa fila de\(L\), también aparece exactamente una vez en fila\(k\) de\(L'\).

Así,\(L'\) satisface la definición de cuadrado latino.

2) Hay tres formas diferentes de completar el cuadrado:

\( 1 \; \; 3 \; \; 4\; \; 2\;\;\;\;\; 1 \; \; 3 \; \; 4\; \; 2 \;\;\;\;\; 1 \; \; 3 \; \; 4\; \; 2 \\ 2 \; \; 1 \; \; 3\; \; 4\;\;\;\;\; 3 \; \; 1 \; \; 2\; \; 4 \;\;\;\;\; 3 \; \; 1 \; \; 2\; \; 4 \\ 4 \; \; 2 \; \; 1\; \; 3\;\;\;\;\; 2 \; \; 4 \; \; 1\; \; 3 \;\;\;\;\; 4 \; \; 2 \; \; 1\; \; 3 \\ 3 \; \; 4 \; \; 2\; \; 1\;\;\;\;\; 4 \; \; 2 \; \; 3\; \; 1 \;\;\;\;\; 2 \; \; 4 \; \; 3\; \; 1 \)

Por lo que la finalización no es única.

Soluciones al Ejercicio 16.2.1

2) Como se explica en el primer párrafo de la prueba del Teorema 16.2.1, podemos suponer que la primera fila es\(1\),\(2\),\(3\),\(4\).

Ahora, utilizamos la idea que se explica en el segundo párrafo de la prueba del Teorema 16.2.1. Para cualquier posición en fila después de la primera fila, la entrada en nuestra nueva plaza latina no puede ser la misma que la entrada en esta posición de ninguna de las dos casillas dadas (porque, para cualquiera\(j\), el par ordenado ya\((j, j)\) ha aparecido en la fila superior de la plaza dada y nuestra nueva plaza), y también no puede ser lo mismo que la entrada en la primera fila de la columna. Esto elimina tres posibilidades para la entrada en esta posición, por lo que sólo queda una posibilidad. Poner esta entrada restante en cada posición arroja el siguiente cuadrado latino, que debe ser el que se solicitó:

\( 1 \; \; 2 \; \; 3\; \; 4 \\ 2 \; \; 1 \; \; 4\; \; 3 \\ 3 \; \; 4 \; \; 1\; \; 2 \\ 4 \; \; 3 \; \; 2\; \; 1 \)

3)

\( 1 \; \; 2 \; \; 3\; \; 4\;\;5\;\;6\;\;7\;\;8 \\ 3 \; \; 4 \; \; 1\; \; 2\;\;7\;\;8\;\;5\;\;6 \\ 5 \; \; 6 \; \; 7\; \; 8\;\;1\;\;2\;\;3\;\;4 \\ 7 \; \; 8 \; \; 5\; \; 6\;\;3\;\;4\;\;1\;\;2 \\ 4\;\;3\;\;2\;\;1\;\;8\;\;7\;\;6\;\;5 \\ 2\;\;1\;\;4\;\;3\;\;6\;\;5\;\;8\;\;7 \\ 8\;\;7\;\;6\;\;5\;\;4\;\;3\;\;2\;\;1 \\ 6\;\;5\;\;8\;\;7\;\;2\;\;1\;\;4\;\;3 \)

Soluciones al Ejercicio 16.3.1

2) Esta colección no tiene sistema de representantes distintos, porque los cinco conjuntos\(A_2\),\(A_3\),\(A_4\),\(A_5\), y\(A_6\) tienen unión\(A_2 ∪ A_3 ∪ A_4 ∪ A_5 ∪ A_6 = \{v, w, x, y\}\), que tiene cardinalidad\(4\).

4) Esta colección sí cuenta con un sistema de representantes distintos:\(x\)\(y\),\(z\), y\(A_1\), para\(A_2\), y\(A_3\) (respectivamente).

Soluciones al Ejercicio 16.3.2

1) Adam, Ella, Jusin y Bryant son solo amigos que han visitado Inglaterra, Escocia, Irlanda, Francia o Italia. Por lo tanto, solo tiene\(4\) amigos entre los que elegir para responder las preguntas de estos\(5\) países. Dado que el número de amigos es menor que el número de países, no puede elegir un amigo diferente para cada uno de estos países.

2) No, esto no se puede completar a un cuadrado\(4 × 4\) latino:

• El tercer ingreso en la tercera fila debe ser\(1\), porque\(2\),\(3\), y\(4\) ya aparece ya sea en la tercera fila o en la tercera columna.
• El último ingreso en la tercera fila también debe ser\(1\), porque\(2\),\(3\), y\(4\) ya aparece ya sea en la tercera fila o en la última columna.

Entonces no podemos completar la tercera fila: nos vemos obligados a haber\(1\) aparecido dos veces en esta fila, pero eso no está permitido.

El Teorema del Matrimonio de Hall no aplica a esta situación, pues, como hemos visto, la tercera columna y la cuarta columna deben elegir ambas su entrada para la tercera fila del conjunto\(\{1\}\), que tiene menos de dos elementos. (El teorema 16.3.2 no se aplica porque el cuadrado latino parcial no consiste sólo en filas completas — tiene una fila que sólo se ha rellenado parcialmente.)

Soluciones al Ejercicio 17.1.1

1) Numéricamente, esta propiedad es fácil de verificar a partir de la prueba del Teorema 17.1.3, que nos dice que si\(b\) es el número de bloques\(b = \dfrac{λv(v − 1)}{k(k − 1)}\), entonces, así (dividiendo ambos lados por\(2\) y multiplicando por\(k(k − 1)\)) tenemos\(b \binom{k}{2} = λ \binom{v}{2}\).

La correspondencia se debe a la coloración explicada en el Teorema 17.1.2.

2) Se nos da eso\(v = 16\),\(k = 6\), y\(λ = 3\).

A partir de la fórmula\(r(k − 1) = λ(v − 1)\), vemos que

\(r = \dfrac{λ(v − 1)}{k − 1} = \dfrac{3(16 − 1)}{6 − 1}= 9\),

lo que significa que cada punto está en\(9\) bloques.

Ahora, a partir de la fórmula\(bk = vr\), tenemos

\(b = \dfrac{vr}{k} = \dfrac{16 · 9}{6} = 24\).

Esto significa que el diseño tiene\(24\) bloques.

Soluciones al Ejercicio 17.2.1

1) PRUEBA. Claramente el complemento de un diseño seguirá teniendo\(v\) variedades. (También contará con\(b\) bloques, ya que cada uno de sus bloques proviene de un bloque del diseño original.)

A partir\(B\) de un bloque de tamaño\(k\), el bloque correspondiente del diseño complementario tendrá los\(v − k\) elementos de\(V \setminus B\).

Necesitamos contar cuántas veces aparece un par de variedades en conjunto en un bloque del diseño complementario. Dos variedades aparecen juntas en un bloque del diseño complementario si y sólo si ninguna de ellas estaba en el bloque correspondiente del diseño original. Cada una de las dos variedades apareció en\(r\) bloques del diseño original, y aparecen juntas en\(λ\) bloques del diseño original. Ahora podemos usar inclusión-exclusión para contar el número de bloques en los que aparece al menos una de las dos variedades:\(r + r − λ = 2r − λ\). Así, el número de bloques en los que ninguno de ellos aparece es\(b − (2r − λ) = b − 2r + λ\), como se afirma. Dado que este recuento de ninguna manera dependía de la elección de nuestras dos variedades, el complemento es de hecho un diseño, ya que cada par de variedades aparecen juntas en algunos\(b − 2r + λ\) tiempos de bloque.

3) El conjunto\(\{1, 3, 7\}\) da las diferencias\(±2\),\(±4\), y\(±6\), mientras que el conjunto\(\{1, 6, 13\}\) da las diferencias\(±5\),\(±7\), y\(±12\). Entonces necesitamos encontrar dos conjuntos que contengan las diferencias\(±1\),,\(±3\)\(±8\),\(±9\),\(±10\), y\(±11\). Los sets\(\{1, 2, 11\}\) y el\(\{1, 4, 12\}\) trabajo.

Soluciones al Ejercicio 17.3.1

1) Muchos ejemplos son posibles (pero pueden ser difíciles de encontrar). Por ejemplo, vamos

\(v = 16, k = 6, \text{ and } λ = 1\).

Entonces

\(λ \dfrac{v − 1}{k − 1} = 1 · \dfrac{16 − 1}{6 − 1} = 3\)

y

\(λ \dfrac{v(v − 1)}{k(k − 1)} = 1 · \dfrac{16(16 − 1)}{6(6 − 1)} = \dfrac{16 · 15}{6 · 5} = 8\)

son enteros, por lo que se satisfacen las condiciones en el Teorema 17.1.2.

A partir de la fórmula\(r(k − 1) = λ(v − 1)\), vemos que

\(r = \dfrac{λ(v − 1)}{k − 1} = 1 · \dfrac{(16 − 1)}{6 − 1} = 3\).

Entonces, a partir de la fórmula\(bk = vr\), tenemos

\(b = \dfrac{vr}{k} = \dfrac{16 · 3}{6} = 8\).

Por lo tanto\(b = 8 < 16 = v\), así que la desigualdad de Fisher no está satisfecha.

Dado que la Desigualdad de Fisher no está satisfecha, no hay BIBD con estos parámetros.

2) Se muestra justo antes de la prueba de la Desigualdad de Fisher a la que equivale la Desigualdad de Fisher\(λ(v − 1) ≥ k(k − 1)\). Desde\(λ = 1\) y\(k = 20\), esto significa

\(1 · (v − 1) ≥ 20(20 − 1) = 380\),

así\(v ≥ 380 + 1 = 381\). Por lo tanto,\(v\) debe ser al menos\(381\) para satisfacer la Desigualdad de Fisher. Desde

\(λ \dfrac{v − 1}{k − 1} = 1 · \dfrac{381 − 1}{20 − 1} = \dfrac{380}{19} = 20\)

y

\(λ \dfrac{v(v − 1)}{k(k − 1)} = 1 · \dfrac{381(381 − 1)}{20(20 − 1)} = \dfrac{381(380)}{380} = 381\)

son enteros, también se cumplen las condiciones en el Teorema 17.1.2. Así\(381\) es el valor más pequeño para\(v\) que satisfaga las tres condiciones.

Soluciones al Ejercicio 18.1.1

2) Ya que\(v = 39 = 6 · 6 + 3 ≡ 3 (\text{mod } 6)\), la prueba del Teorema 18.1.1 nos dice que debemos usar un cuadrado latino construido en Lema 18.1.1. Ya que\(\dfrac{v}{3} = \dfrac{39}{3} = 13\), el cuadrado latino es de orden\(n = 13\), por lo que la primera frase de la prueba de Lema 18.1.1 nos dice que la primera fila del cuadrado latino es

\(1 \;\;\;\; \dfrac{13 + 3}{2} \;\;\;\; 2 \;\;\;\; \dfrac{13 + 5}{2} \;\;\;\; 3 \;\;\;\; \dfrac{13 + 7}{2} \;\;\;\; 4 \;\;\;\; · · · \;\;\;\; 13 \;\;\;\; \dfrac{13 + 1}{2}.\).

En otras palabras, la primera fila es

\(1 \;\;\;\; 8 \;\;\;\; 2 \;\;\;\; 9 \;\;\;\; 3 \;\;\;\; 10 \;\;\;\; 4 \;\;\;\; 11 \;\;\;\; 5 \;\;\;\; 12 \;\;\;\; 6 \;\;\;\; 13 \;\;\;\; 7\).

Entonces la segunda frase de la prueba de Lema 18.1.1 nos dice que el resto de las filas se obtienen desplazándose hacia la izquierda. Entonces el cuadrado latino es

\( 1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7 \\ 8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1 \\ 2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8 \\ 9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2 \\ 3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9 \\ 10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3 \\ 4\;\;11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10 \\ 11\;\;5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4 \\ 5\;\;12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11 \\ 12\;\;6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5 \\ 6\;\;13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12 \\ 13\;\;7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6 \\ 7\;\;1\;\;8\;\;2\;\;9\;\;3\;\;10\;\;4\;\;11\;\;5\;\;12\;\;6\;\;13 \\ \)

4) No, no es un sistema Kirkman.

Llamaremos a\(\{u_1, . . . , u_5\}\) las u-girls; a\(\{v_1, . . . , v_5\}\) las v-girls; y a\(\{w_1, . . . , w_5\}\) las w-girls. De los\(35\) bloques que obtuvimos a través de la construcción,\(5\) tenemos una\(u\) -chica, una\(v\) -chica, y una\(w\) -chica; la otra\(30\) tienen o dos\(u\) -chicas con una\(v\) -chica, dos\(v\) -chicas con una\(w\) -chica, o dos\(w\) -chicas con una\(u\) -chica.

Un sistema Kirkman requiere que dividamos los bloques en\(7\) grupos de\(5\) bloques de tal manera que cada chica aparezca exactamente una vez en cada grupo de bloques. Ya que debe haber\(7\) grupos de\(5\) bloques, pero solo hay\(5\) bloques que tengan una\(u\) -chica, una\(v\) -chica, y una\(w\) -chica, debe haber al menos un grupo de bloques (de hecho, al menos dos) que no tenga bloque consistente en una\(u\) -chica, una\(v\) -chica , y una\(w\) -chica.

Considera tal grupo de\(5\) bloques. Debemos tener todas\(5\) las\(u\) -chicas. Si ningún bloque contenía más de una\(u\) -chica, entonces para conseguir todas\(5\)\(u\) -chicas tendríamos que elegir solo bloques que tengan dos\(w\) -chicas y una\(u\) -chica. No obstante, esto significaría que teníamos\(10\)\(w\) -chicas y no\(v\) -chicas, lo cual no está permitido. Entonces debemos elegir al menos una cuadra que tenga dos\(u\) -chicas y una\(v\) -chica. Repitiendo el mismo argumento con\(v\) o\(w\) tomando el lugar de\(u\), vemos que también debemos elegir al menos un bloque que tenga dos\(v\) -chicas y una\(w\) -chica, y al menos un bloque que tenga dos\(w\) -chicas y una\(u\) -chica. Ya que solo estamos eligiendo\(5\) bloques pero hay estas tres clases de bloques, debe haber alguna clase de bloques de los cuales solo elegimos uno.

Sin pérdida de generalidad, supongamos que solo elegimos uno de los bloques que tiene dos\(u\) -chicas y una\(w\) -chica. Para tener todas\(5\) las\(u\) -chicas, debemos elegir tres cuadras que tengan dos\(w\) -chicas y una\(u\) -chica. Pero esto quiere decir que tenemos seis\(w\) -chicas, lo cual no está permitido.

Por lo tanto, no hay forma de dividir los bloques de este diseño en siete grupos de cinco bloques para que cada chica aparezca exactamente una vez en cada grupo.

Soluciones al Ejercicio 18.2.1

2) Debemos tener\(b \binom{k}{t} = λ \binom{v}{t} = \binom{15}{t}\).

Ya que no estamos incluyendo ningún\(t−(v, t, 1)\) diseño trivial, tenemos\(t ≥ 2\),\(3 ≤ k ≤ 14\), y\(t < k\).

Ahora

\(\dfrac{15!}{t!(15 − t)!} = b \dfrac{k!}{t!(k − t)!}\),

lo que significa que

\(\dfrac{15 · 14 · · ·(16 − t)}{k(k − 1)· · ·(k + 1 − t)}\)

es un número entero.

Además, tenemos\(\binom{k − 1}{t − 1}\) divisiones\(\binom{14}{t − 1}\), así que eso\(\binom{(k − 1)!}{(k − t)!}\) divide\(\binom{14!}{(15 − t)!}\). En otras palabras,

\(\dfrac{14!(k − t)!}{(15 − t)!(k − 1)!} = \dfrac{14 · 13 · · ·(16 − t)}{(k − 1)(k − 2)· · ·(k + 1 − t)}\)

es un número entero. Si llamamos a este entero\(y\), combinarlo con el párrafo anterior nos dice que\(k\) es un divisor de\(15y\). También podemos seguir trabajando con el álgebra para obtener

\(y = \dfrac{14 · 13 · · · k}{(15 − t)(14 − t)· · ·(k + 1 − t)}\).

Cuando\(k = 14\), esto da\(y = \dfrac{14}{(15 − t)}\). Ya que\(k\) divide\(15y\) y\(k\) es coprime a\(15\), debemos tener\(k\) divisiones\(y\). Pero entonces\(\dfrac{y}{14} = \dfrac{1}{(15 − t)}\) es un entero, lo que implica\(t = 14\). Esto contradice\(t < k\). Así\(k = 14\) no puede surgir.

Cuando\(k = 13\) esto da\(y = \dfrac{14 · 13}{(15 − t)(14 − t)}\). Ya que\(k\) divide\(15y\) y\(k\) es coprime a\(15\), debemos tener\(k\) divisiones\(y\). Pero entonces\(\dfrac{y}{13} = \dfrac{14}{(15 − t)(14 − t)}\) es un entero. Ya que\(t < k = 13\), tenemos\(14 − t ≥ 2\), pero no hay dos enteros consecutivos cada uno de los cuales es al menos ambos\(2\) son divisores de\(14\), una contradicción. Así\(k = 13\) no puede surgir.

Cuando\(k = 12\), esto da

\(y = \dfrac{14 · 13 · 12}{(15 − t)(14 − t)(13 − t)} \).

Ahora\(k\) dividir\(15y\) implica que

\(\dfrac{15 · 14 · 13}{(15 − t)(14 − t)(13 − t)}\)

es un número entero. Dado que el numerador no es múltiplo de\(2^2\), el denominador tampoco puede ser, dejando sólo las posibilidades\(t = 4\),\(8\). Dado que el numerador no es múltiplo de\(3^2\), el denominador no puede ser ninguno, lo que elimina\(t = 4\). Cuando\(t = 8\), el numerador de no\(y\) es múltiplo de\(5\), sino el denominador lo es, por lo que esto también es imposible. Así\(k = 12\) no puede surgir.

Cuando\(k = 11\) esto da

\(y = \dfrac{14 · 13 · 12 · 11}{(15 − t)(14 − t)(13 − t)(12 − t)} \).

Ya que\(k\) divide\(15y\) y\(k\) es coprime a\(15\), debemos tener\(k\) divisiones\(y\). Pero entonces

\(\dfrac{y}{11} = \dfrac{14 · 13 · 12}{(15 − t)(14 − t)(13 − t)(12 − t)}\)

es un número entero. Dado que el numerador no es múltiplo de\(5\), los cuatro números consecutivos que son los factores del denominador deben ser\(6\) a través\(9\) (ya que\(t ≥ 2\), no pueden ser\(11\) a través\(14\), y ya que no\(t < 11\) pueden ser\(1\) a través\(4\)). Por lo tanto, debemos tener\(t = 6\). Pero entonces el numerador no es divisible por\(3^2\), mientras que el denominador es divisible por\(3^3\), contradiciendo\(\dfrac{y}{11}\) ser un entero. Por lo tanto, no\(k = 11\) es posible.

Cuando\(k = 10\), esto da

\(y = \dfrac{14 · 13 · 12 · 11 · 10}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)}\).

Ahora\(k\) dividir\(15y\) implica que

\(\dfrac{15 · 14 · 13 · 12 · 11}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)}\)

es un número entero. Como el numerador no es múltiplo de\(2^4\), el denominador tampoco puede serlo. En particular,\(8\) no puede ser uno de los factores que aparece en el denominador (ya que algún otro factor incluso aparecería con él), ni puede\(2\)\(4\),, y\(6\) todos ser factores que aparecen en el denominador. Además, el numerador no es divisible por\(3^3\), así que no podemos tener\(11 − t = 9\). Esto deja\(t = 8\) como única posibilidad. Sin embargo, el numerador de no\(y\) es divisible por\(3^2\), por lo que tampoco\(t = 8\) es posible. Por lo tanto, no\(k = 10\) es posible.

Cuando\(k = 9\), vemos que

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)}\).

Así que\(k\) dividir\(15y\) da

\(\dfrac{15 · 14 · 13 · 12 · 11 · 10}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)}\)

siendo un entero. Como el numerador no es divisible por\(2^5\), el denominador tampoco puede serlo. En particular,\(8\) no puede aparecer como uno de los factores en el denominador (o otros dos números divisibles por también\(2\) aparecerían como factores), por lo que la única posibilidad es\(t = 8\). No obstante, si tomamos\(k = 9\),\(t = 8\), y\(i = 2\), la condición necesaria es\(7\binom{7}{6} = 7\) divide\(\binom{13}{6}\), lo cual no es cierto. Así, no\(k = 9\) es posible.

Cuando\(k = 8\), calculamos

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)}\).

Ya que\(k\) divide\(15y\) y\(k\) es coprime a\(15\), debemos tener\(k\) divisiones\(y\). Pero entonces

\(\dfrac{y}{8} = \dfrac{14 · 13 · 12 · 11 · 10 · 9}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)}\).

Dado que los factores consecutivos en el denominador incluyen\(8\) y al menos otros dos números pares, esto implica que el numerador también debe ser un múltiplo de\(2^5\), pero no lo es. Por lo tanto, no\(k = 8\) es posible.

Cuando\(k = 7\) vemos que

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)}\).

Ya que los factores consecutivos en el denominador incluyen\(6\) y\(9\), si también incluyen otro múltiplo de\(3\) entonces el numerador debe ser divisible por\(3^4\), pero no lo es. Esto deja la posibilidad de que\(t = 4\) así los factores en el denominador sean\(4\) a través\(11\), pero esto es divisible por\(5^2\), lo que no lo es el numerador. Así, no\(k = 7\) es posible.

Si\(k = 6\) entonces

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)}\).

Así que\(k\) dividir\(15y\) da

\(\dfrac{15 · 14 · 13 · 12 · 11 · 10 · 9 · 8 · 7}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)}\)

siendo un entero. El numerador no es divisible por\(2^8\), por lo que el denominador tampoco puede ser; en particular no puede incluir como factores todos los enteros pares de\(4\) a través así\(10\) como entre sí. Esto deja las posibilidades\(t = 2\) y\(t = 4\). Si\(t = 2\) entonces\(y = \dfrac{14}{5}\) que no es un entero, y de manera similar si\(t = 4\) entonces tenemos\(y = \dfrac{14 · 13 · 12}{5 · 4 · 3}\) que no es un entero. Entonces no\(k = 6\) es posible.

Si\(k = 5\) entonces

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6 · 5}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)(6 − t)}\).

El numerador no es divisible por\(2^9\), por lo que el denominador no puede ser ninguno; en particular, el denominador no puede incluir todos\(4\)\(6\),\(8\),\(10\),, y\(12\) como factores en el producto. Esto sólo deja la posibilidad\(t = 4\). Si\(k = 5\) y\(t = 4\) luego\(i = 0\) da\(\binom{5}{4} = 5\) divisiones\(\binom{15}{4} = 1365\) que es verdad;\(i = 1\) da\(\binom{4}{3} = 4\) divisiones\(\binom{14}{3} = 364\) que es verdad;\(i = 2\) da\(\binom{3}{2} = 3\) divisiones\(\binom{13}{2} = 78\), que es verdad;\(i = 3\) da\(\binom{2}{1} = 2\) divisiones\(\binom{12}{1} = 12\), que es verdad. Así un\(4\) −\((15, 5, 1)\) diseño podría existir, pero esta es la única posibilidad con\(k = 5\).

Cuando\(k = 4\) tenemos

\(y = \dfrac{14 · 13 · 12 · 11 · 10 · 9 · 8 · 7 · 6 · 5 · 4}{(15 − t)(14 − t)(13 − t)(12 − t)(11 − t)(10 − t)(9 − t)(8 − t)(7 − t)(6 − t)(5 − t)}\)

El denominador incluye\(3\),\(6\),\(9\), y\(12\), así es divisible por\(3^5\), pero el numerador no lo es. Así, no\(k = 4\) es posible.

Si\(k = 3\) entonces\(2 ≤ t < k\) implica\(t = 2\). Sabemos que estos parámetros son posibles, ya que estos son los parámetros de un sistema triple Steiner.

Así, los únicos valores posibles de\(k\) y\(t ≥ 2\) para los cuales podrían existir\(t\) diseños no triviales con\(v = 15\) y\(λ = 1\) son\(k = 5\) y\(t = 4\): a\(4\) −\((15, 5, 1)\) diseño, o\(k = 3\) y\(t = 2\): un sistema triple\((15, 3, 1)\) Steiner.

3) Si existe un\(3\) −\((16, 6, 1)\) diseño entonces tenemos\(bk = vr\) y\(b \binom{k}{t} = λ \binom{v}{t}\). La segunda ecuación da\(b \binom{6}{3} = \binom{16}{3}\)\(b = 28\), entonces, entonces tendría\(28\) bloques. Ahora\(bk = vr\) da\(28 · 6 = 16r\). Esto no tiene una solución integral, por lo que dicho diseño no es posible.

Soluciones al Ejercicio 18.3.1

1) PRUEBA. Dejar\(L\),\(M\), y\(N\) ser líneas de un plano afín tal que\(L\) sea paralelo a ambos\(M\) y\(N\); es decir, no hay punto en ambos\(L\) y\(M\) ni en ambos\(L\) y\(N\). Dejemos\(p\) ser un punto arbitrario sobre\(M\). Ya que\(L\) y\(M\) son paralelos,\(p\) no se acuesta sobre\(L\). Por el postulado paralelo, hay una línea única a través de la\(p\) que es paralela a\(L\); esta línea es\(M\). Por lo tanto\(N\) no puede contener\(p\). Dado que nuestra elección de\(p\) on\(M\) fue arbitraria, ningún punto de también\(M\) puede mentir\(N\), así\(M\) y\(N\) son paralelos.

3) Un plano afín finito de orden\(19\) tiene\(19^2 = 361\) puntos y\(19(19 + 1) = 380\) líneas.

5) Sin colores es difícil dibujar efectivamente este plano para que se puedan ver claramente las clases paralelas. Utilizaremos líneas verticales continuas; líneas horizontales sólidas; líneas discontinuas; líneas punteadas; líneas grises continuas; y líneas grises punteadas para representar las seis clases paralelas de líneas, pero algunas de ellas pueden ser difíciles de distinguir. Tenga en cuenta que las líneas que no son ni verticales ni horizontales “girarán esquinas” o zig-zag para unir sus conjuntos de\(5\) puntos.

Obtenemos los siguientes\(4\) MOLS de orden\(5\) a partir de este plano afín, utilizando las líneas verticales y horizontales para crear las coordenadas. Para que las cosas sean más fáciles de ver, tendremos las posiciones en los cuadrados latinos que correspondan visualmente a las posiciones en el\(5\) array\(5\) by de puntos que hemos dibujado, por lo que la entrada superior izquierda en los cuadrados latinos vendrá del punto superior izquierdo de la matriz, etc. numeraremos las líneas en cada una paralelo a fin de asegurar que las entradas en la fila superior de cada cuadrado son\(1\),\(2\),\(3\),\(4\), y\(5\), en ese orden. El primer cuadrado corresponde a las líneas discontinuas; el segundo a las líneas punteadas; el tercero a las líneas grises sólidas y el cuarto a las líneas grises discontinuas.

\( 1\;\;2\;\;3\;\;4\;\;5 \;\;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \;\;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \;\;\;\; 1\;\;2\;\;3\;\;4\;\;5 \\ 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\;\; 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \\ 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \\ 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\;\; 3\;\;4\;\;5\;\;1\;\;2 \;\;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\; 5\;\;1\;\;2\;\;3\;\;4 \\ 5\;\;1\;\;2\;\;3\;\;4 \;\;\;\;\; 2\;\;3\;\;4\;\;5\;\;1 \;\;\;\;\; 4\;\;5\;\;1\;\;2\;\;3 \;\;\;\; 3\;\;4\;\;5\;\;1\;\;2 \)

Soluciones al Ejercicio 18.4.1

1) No, no todos los diseños con\(λ = 1\) son un plano proyectivo. La condición\(λ = 1\) asegura que cada dos puntos tengan una línea única que sea incidente con ambos. Sin embargo, en un diseño no se requiere que cada dos bloques tengan una intersección no vacía. (Si cada dos bloques tienen una intersección no vacía, entonces la condición\(λ = 1\) obliga a la intersección a tener exactamente un punto). La condición de que existan cuatro puntos tales que no tres sean incidentes con una sola línea también puede fallar, sino sólo en situaciones triviales o completas.

3) A partir del Teorema 16.2.2, sabemos que hay\(p − 1\) MOLS de orden\(p\) cada vez que\(p\) es primo. Esto implica que hay un plano proyectivo que tiene\(p + 1\) puntos en cada línea siempre que\(p\) sea primo.

4) Como no hay\(5\) MOLS de orden\(6\) (como vimos en el problema de Euler), no hay plano proyectivo que tenga\(7\) puntos en cada línea.

Soluciones al Ejercicio 19.1.1

La única cadena con un número impar de\(1\) s es\(10101\), por lo que no es un mensaje permisible, pero todos los demás están permitidos.

Soluciones al Ejercicio 19.2.2

1) La única palabra así es “matemáticas”.

3) Hay muchas posibilidades, como “\(\text{\(\underline{\text{b}}\)at\(\underline{\text{s}}\)}\),” “\(\text{\(\underline{\text{g}}\)a\(\underline{\text{s}}\) h}\),” y “\(\text{ma\(\underline{\text{n}}\)\(\underline{\text{y}}\)}\)”.

5) Esto lo hemos respondido en cada solución dada anteriormente.

Soluciones al Ejercicio 19.2.3

2) PRUEBA. Dejar\(x\) y\(y\) ser palabras de la misma longitud. Tenemos\(d(x, y) = 0\) si y sólo si\(x\) y\(y\) difieren en ninguna posición. Esto quiere decir que\(x\) debe tener la misma entrada que\(y\) en cada posición, lo que significa\(x = y\).

4) PRUEBA. Dejar\(x\),\(y\), y\(z\) ser palabras de la misma longitud. Supongamos que\(d(x, z) = k\), para que\(x\) y\(z\) difieran en\(k\) posiciones. Supongamos que\(d(x, y) = i\), así\(y\) difiere de\(x\) en\(i\) posiciones. Si\(i ≥ k\) entonces desde\(d(y, z) ≥ 0\) por la parte (1), tenemos\(d(x, z) ≤ d(x, y)+d(y, z)\). De lo contrario, debe haber alguna lista de al menos\(k − i\) posiciones en las que\(x\) difiera de\(z\) pero no difiera de las mismas\(y\). En cada una de estas posiciones, ya que\(y\) tiene la misma entrada que\(x\),\(y\) debe tener una entrada diferente a la\(z\). Por lo tanto\(d(y, z) ≥ k −i\). Ahora\(d(x, y) +d(y, z) ≥ i + k − i = k = d(x, z)\), completando la prueba.

Soluciones al Ejercicio 19.2.4

3) La distancia mínima es\(2\). Para ver esto, primero tenga en cuenta que\(d(01011, 10011) = 2\), por lo que la distancia mínima no es mayor que\(2\). Dado que cada una de las palabras de código distintas de cero tiene exactamente tres\(1\) s\(3\), su distancia de\(00000\) es, y su distancia a cualquier otra palabra de código distinta de cero es mayor que\(1\) porque cambiar un solo bit cambiará el número\(1\) de s. entonces la distancia mínima es al menos\(2\).

Soluciones al Ejercicio 19.2.5

2) (a) El código puede detectar\(5\) errores, pero no\(6\) (porque el número de errores detectados debe ser menor que la distancia mínima).

(b) El código puede corregir\(2\) errores (porque\(2 × 2 < 6\), pero\(2 × 3 \nless 6\)).

Soluciones al Ejercicio 19.3.1

1) Desde

\( G = \left[ \begin{array}{ll} I_k \\ A \end{array} \right] = \left[ \begin{array}{ll} 1\;\;0\;\;0\;\;0 \\ 0\;\;1\;\;0\;\;0 \\ 0\;\;0\;\;1\;\;0 \\ 0\;\;0\;\;0\;\;1 \\ 1\;\;1\;\;0\;\;0 \\ 1\;\;0\;\;0\;\;1 \end{array} \right] \)

tenemos

\( G = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \\ 1 \\ 1 \\ 1 \end{array} \right], \;\;\;\;\;\;\;\; G = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{array} \right], \;\;\;\;\;\;\;\; G = \left[ \begin{array}{ll} 1 \\ 1 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 1 \end{array} \right] \)

Esto significa que\(0101\) codifica como\(010111\),\(0010\) codifica como\(001000\) y\(0010\) codifica como\(111001\).

Soluciones al Ejercicio 19.4.2

Ya que\( G = \left[ \begin{array}{ll} I_k \\ A \end{array} \right]\), y la matriz dada\(G\) tiene\(4\) columnas, debemos tener\(k = 4\), también lo\(I_k = I_4\) ha hecho\(4\) filas. Por lo tanto,\(A\) es todo menos las primeras\(4\) filas de\(G\), lo que significa

\(A = \left[ \begin{array}{ll} 1\;\;0\;\;1\;\;1 \\ 1\;\;0\;\;0\;\;1 \\ 0\;\;1\;\;1\;\;1 \end{array} \right] \)

Ya que\(A\) es una\(3 × 4\), matriz, tenemos\(r = 3\), así que la matriz de comprobación de paridad es

\( P = [A \;\; I_r] = [A \;\; I_3] = \left[ \begin{array}{ll} 1\;\;0\;\;1\;\;1\;\;1\;\;0\;\;0 \\ 1\;\;0\;\;0\;\;1\;\;0\;\;1\;\;0 \\ 0\;\;1\;\;1\;\;1\;\;0\;\;0\;\;1 \end{array} \right] \)

Soluciones al Ejercicio 19.4.4

2) (a) Sí, las seis columnas de la matriz de comprobación de paridad son diferentes entre sí (y ninguna de ellas lo es todas\(0\)), por lo que el Teorema 19.4.1 nos dice que el código puede corregir todos los errores de un solo bit.

b)\(P\) Sea la matriz de comprobación de paridad dada. Entonces:

• \(G = \left[ \begin{array}{ll} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 1 \\ 0 \end{array} \right].\;\;\;\;\)Esta es la\(5^{\text{th}}\) columna de\(P\), por lo que cambiar el\(5^{\text{th}}\) bit corrige el error. La palabra recibida\(001001\) decodifica como\(0010 \underline{1} 1\).
• \(G = \left[ \begin{array}{ll} 1 \\ 1 \\ 0 \\ 0 \\ 1 \\ 1 \end{array} \right] = \left[ \begin{array}{ll} 0 \\ 0 \\ 0 \end{array} \right].\;\;\;\;\)Esto es\(0\), por lo que no hay error. La palabra recibida\(110011\) decodifica como\(110011\).
• \(G = \left[ \begin{array}{ll} 0 \\ 0 \\ 0 \\ 1 \\ 1 \\ 0 \end{array} \right] = \left[ \begin{array}{ll} 1 \\ 1 \\ 0 \end{array} \right].\;\;\;\;\)Esta es la\(2^{\text{nd}}\) columna de\(P\), por lo que cambiar el\(2^{\text{nd}}\) bit corrige el error. La palabra recibida\(000110\) decodifica como\(0 \underline{1} 0110\).

Soluciones al Ejercicio 19.4.5

1) Hay\(2^5 − 1 = 31\) diferentes cadenas de\(5\) bits distintas de cero. De estas\(31\) cuerdas,\(5\) de ellas solo tienen una\(1\). Así, existen\(31 − 5 = 26\) diferentes cadenas distintas de cero con al menos dos\(1\) s. Por lo tanto, podemos hacer una\(5 × 24\) matriz\(A\), de tal manera que las columnas de\(A\) son\(24\) diferentes vectores de columna binarios con al menos dos\(1\) s en cada columna (porque hay\(26\) diferentes columnas posibles para elegir, y solo necesitamos\(24\) de ellas). Las columnas de la matriz de comprobación de paridad resultante\(P = [A \;\;I_5]\) son todas distintas de cero y distintas, por lo que el Teorema 19.4.1 nos dice que el código lineal binario resultante puede corregir cada error de un solo dígito.

Además, ya que\(P\) es\(5 × 24\), sabemos que\(r = 5\) y\(k = 24\). Ya que\(r = n − k\), esto implica\(n = k+r = 24+ 5 = 29\). Entonces el código es de tipo\((n, k) = (29, 24)\), según se desee.

3) Supongamos que\(P\) es la matriz de comprobación de paridad de un código lineal binario de tipo\((n, k)\) que corrige todos los errores de un solo bit, y let\(r = n − k\). Entonces el Teorema 19.4.1 nos dice que las columnas de\(P\) deben ser distintas (y distintas de cero). Sin embargo,\(P\) es\(r × n\), y\(n = k + r\), por lo que tiene\(k + r\) columnas de longitud r, y solo hay\(2^r − 1\) diferentes columnas posibles distintas de cero de longitud\(r\). Por lo tanto, debemos tener\(k + r ≤ 2^r − 1\). Por el contrario, si se satisface esta desigualdad, entonces podemos construir una matriz de\(k × (k + r)\) verificación de paridad cuyas columnas sean todas distintas y distintas de cero. Así, el menor número posible de bits de comprobación es el valor más pequeño\(r\) que satisface la desigualdad\(k + r ≤ 2^r − 1\).

Así:

• \(r = 2\)bits de verificación son suficientes para\(k = 1\), porque\(k + r = 1 + 2 = 3 = 2^2 − 1 = 2^r − 1\). (Pero el bit de\(r = 1\) verificación no es suficiente, porque\(k +r ≥ 1 + 1 = 2 > 2^1 −1 = 2^r −1\)).
• \(r = 3\)bits de verificación son suficientes para\(k = 2, 3, 4\), porque\(k +r ≤ 4 + 3 = 7 = 2^3 −1 = 2^r −1\). (Pero los bits de\(r = 2\) verificación no son suficientes, porque\(k + r ≥ 2 + 2 = 4 > 2^2 − 1 = 2^r − 1\)).
• \(r = 4\)bits de verificación son suficientes para\(5 ≤ k ≤ 11\), porque\(k+r ≤ 11+4 = 15 = 2^4−1 = 2^r−1\). (Pero los bits de\(r = 3\) verificación no son suficientes, porque\(k + r ≥ 5 + 3 = 8 > 2^3 − 1 = 2^r − 1\)).
• \(r = 5\)bits de verificación son suficientes para\(12 ≤ k ≤ 20\), porque\(k + r ≤ 20 + 5 = 25 < 31 = 2^5 − 1 = 2^r − 1\). (Pero los bits de\(r = 4\) verificación no son suficientes, porque\(k+r ≥ 12+4 = 16 > 2^4−1 = 2^r −1\)).

Soluciones al Ejercicio 19.5.1

1) Usando la Proposición 19.5.1, tenemos\(v = 10\),\(k − 2 = 4\) para que\(k = 6\), y\(λ = 1\). La pregunta nos está pidiendo\(b\). El uso\(bk(k − 1) = λv(v − 1)\) da\(30b = 90\) así\(b = 3\). Dicho código sólo tendrá\(3\) palabras.