4.E: Sistemas de Representantes Distintos (Ejercicios)
- Page ID
- 117119
4.2: Existencia de DEG
Ejercicio\(\PageIndex{2.1}\)
¿Cuántos sistemas diferentes de representantes distintos hay para\(A_1=\{1,2\}\),\(A_2=\{2,3\}\),...,\(A_n=\{n,1\}\)?
Ejercicio\(\PageIndex{2.2}\)
¿Cuántos sistemas diferentes de representantes distintos hay para los conjuntos\(A_i=[n]\backslash{i}\),\(i=1,2,\ldots,n\),\(n\ge2\)?
Ejercicio\(\PageIndex{2.3}\)
Supongamos que el sistema set\(A_1,A_2,\ldots,A_n\) tiene un sdr, y eso\(x\in A_i\). Mostrar el sistema set tiene un sdr que contiene\(x\). \(x\)Demostrar que no necesariamente se puede elegir para representar\(A_i\).
Ejercicio\(\PageIndex{2.4}\)
Supongamos que el sistema establecido\(A_1,A_2,\ldots,A_n\) satisface\(|\bigcup_{j=1}^k A_{i_j}|\ge k+1\) para cada\(1\le k< n\) y\(\{i_1,i_2,\ldots,i_k\}\subseteq [n]\), y eso\(x\in A_i\). Mostrar el sistema set tiene un sdr en el que\(x\) representa\(A_i\).
Ejercicio\(\PageIndex{2.5}\)
Un\(m\times n\) tablero de ajedrez, con\(m\) par y ambos\(m\) y al\(n\) menos 2, tiene un cuadrado blanco y otro negro quitados. Demuestre que la tabla puede ser cubierta por dominó.
4.3: DEG parciales
Ejercicio\(\PageIndex{3.1}\)
Encuentra el tamaño de un sdr máximo para\[A_1=\{a,b,c\}, A_2=\{a,b,c,d,e\}, A_3=\{a,b\}, A_4=\{b,c\}, A_5=\{a\}, A_6=\{a,c,e\}.\nonumber\] Justifica tu respuesta.
4.4: Cuadrados latinos
Ejercicio\(\PageIndex{4.1}\)
Demostrar que solo hay un cuadrado latino reducido de orden 3.
Ejercicio\(\PageIndex{4.2}\)
Verificar que la relación isotopía es una relación de equivalencia.
Ejercicio\(\PageIndex{4.3}\)
Encuentra todos los 4 cuadrados latinos reducidos de orden 4. Demostrar que hay como máximo 2 clases de isotopía para el pedido 4.
Ejercicio\(\PageIndex{4.4}\)
Mostrar que el sistema del segundo conjunto definido en el Ejemplo 4.4.5 tiene un sdr como se reivindica.
Ejercicio\(\PageIndex{4.5}\)
Demostrar que no hay cuadrados latinos ortogonales de orden 2.
Ejercicio\(\PageIndex{4.6}\)
Encuentra los dos cuadrados ortogonales latinos de orden\(5\) como se describe en el Teorema 4.4.1. Muestra tu respuesta como en el Ejemplo 4.4.6.
Ejercicio\(\PageIndex{4.7}\)
Demostrar que para construir cuadrados latinos ortogonales de orden\(2^m\)\(m\ge2\),, basta con encontrar dos cuadrados latinos ortogonales de orden\(4=2^2\) y dos de orden\(8=2^3\).
Ejercicio\(\PageIndex{4.8}\)
Un cuadrado\(n\times n\) latino\(A\) es simétrico si es simétrico alrededor de la diagonal principal, es decir,\(A_{i,j}=A_{j,i}\) para todos\(i\) y\(j\). Es fácil encontrar cuadrados latinos simétricos: cada módulo de tabla de adición\(n\) es un ejemplo, como en el Ejemplo 4.4.4. Un cuadrado latino es idempotente si cada símbolo aparece en la diagonal principal. Mostrar que si\(A\) es a la vez simétrico e idempotente, entonces\(n\) es impar. Encuentra un cuadrado latino\(5\times 5\) simétrico e idempotente.
Ejercicio\(\PageIndex{4.9}\)
La transposición\(A^\top\) de un cuadrado latino\(A\) es el reflejo de\(A\) través de la diagonal principal, así que eso\(A_{i,j}^\top=A_{j,i}\). Un cuadrado latino es autoortogonal si\(A\) es ortogonal a\(A^\top\). Demostrar que no existe un cuadrado latino autoortogonal de orden 3. Encuentra uno de orden 4.
4.6: Emparejamientos
Ejercicio\(\PageIndex{5.1}\)
En esta gráfica bipartita, encuentra una coincidencia máxima y una mínima cobertura de vértice utilizando el algoritmo de esta sección. Comienza con la coincidencia que se muestra en rojo. Copias de esta gráfica están disponibles en este archivo pdf.
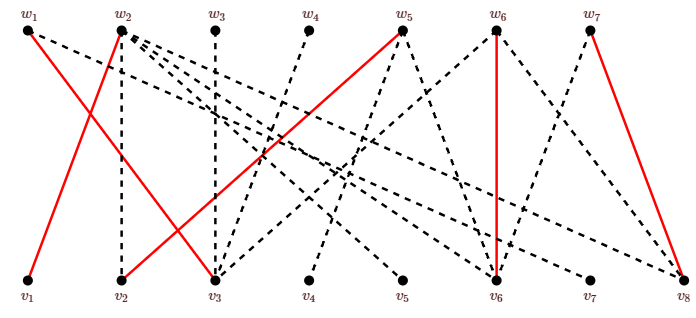
Ejercicio\(\PageIndex{5.2}\)
Mostrar directamente que el tamaño de una cubierta mínima de vértice en\(G\) es el valor mínimo de\(n-k+|\bigcup_{j=1}^k A_{i_j}|\), como se mencionó anteriormente.


