5.5: Árboles
- Page ID
- 117095
Otra clase especial útil de gráficos:
Definición\(\PageIndex{1}\): Acyclic Tree
Una gráfica conectada\(G\) es un árbol si es acíclica, es decir, no tiene ciclos. De manera más general, a una gráfica acíclica se le llama bosque.
En la Figura 5.1.5 se muestran dos pequeños ejemplos de árboles. Tenga en cuenta que la definición implica que ningún árbol tiene un bucle o múltiples aristas.
Teorema \(\PageIndex{1}\)
Cada árbol\(T\) es bipartito.
- Prueba
-
Ya que no\(T\) tiene ciclos, es cierto que cada ciclo de\(T\) tiene una longitud uniforme. Por Corolario 5.4.1,\(T\) es bipartito.
Definición\(\PageIndex{2}\): Pendant Vertex
Un vértice de grado uno se llama vértice colgante, y el borde incidente a él es un borde colgante.
Teorema \(\PageIndex{2}\)
Cada árbol en dos o más vértices tiene al menos un vértice colgante.
- Prueba
-
Demostramos lo contrapositivo. Supongamos que la gráfica no\(G\) tiene vértices colgantes. Comenzando en cualquier vértice\(v\), siga una secuencia de aristas distintas hasta que se repita un vértice; esto es posible porque el grado de cada vértice es de al menos dos, por lo que al llegar a un vértice por primera vez siempre es posible dejar el vértice en otro borde. Cuando un vértice se repite por primera vez, hemos descubierto un ciclo.
Este teorema a menudo proporciona el paso clave en una prueba de inducción, ya que al quitar un vértice colgante (y su borde colgante) se deja un árbol más pequeño.
Teorema \(\PageIndex{3}\)
Un árbol en\(n\) vértices tiene exactamente\(n-1\) bordes.
- Prueba
-
Un árbol en 1 vértice tiene 0 bordes; este es el caso base.
Si\(T\) es un árbol en\(n\ge 2\) vértices, tiene un vértice colgante. Retire este vértice y su borde colgante para obtener un árbol\(T'\) en\(n-1\) vértices. Por la hipótesis de inducción,\(T'\) tiene\(n-2\) bordes; así\(T\) tiene\(n-1\) bordes.
Teorema \(\PageIndex{4}\)
Un árbol con un vértice de grado\(k\ge 1\) tiene al menos vértices\(k\) colgantes. En particular, cada árbol en al menos dos vértices tiene al menos dos vértices colgantes.
- Prueba
-
El caso\(k=1\) es obvio. Dejar\(T\) ser un árbol con\(n\) vértices, secuencia de grados\(\{d_i\}_{i=1}^n\), y un vértice de grado\(k\ge2\), y dejar\(l\) ser el número de vértices colgantes. Sin pérdida de generalidad,\(1=d_1=d_2=\cdots=d_l\) y\(d_{l+1}=k\). Entonces\[2(n-1) = \sum_{i=1}^n d_i = l+k+\sum_{i=l+2}^n d_i \ge l+k+2(n-l-1).\nonumber\] Esto se reduce a\(l\ge k\), según se desee.
Si\(T\) es un árbol en dos vértices, cada uno de los vértices tiene grado 1. Si\(T\) tiene al menos tres vértices debe tener un vértice de grado\(k\ge 2\), ya que de lo contrario\(2(n-1)=\sum_{i=1}^n d_i = n\), lo que implica\(n=2\). De ahí que tenga al menos vértices\(k\ge2\) colgantes.
Los árboles son bastante útiles por derecho propio, pero también para el estudio de las gráficas generales.
Definición\(\PageIndex{3}\): Spanning Trees
Si\(G\) es una gráfica conectada en\(n\) vértices, un árbol de expansión para\(G\) es un subgrafo de\(G\) que es un árbol en\(n\) vértices.
Teorema \(\PageIndex{5}\)
Cada gráfica conectada tiene un árbol de expansión.
- Prueba
-
Por inducción en el número de aristas. Si\(G\) está conectado y tiene cero aristas, es un solo vértice, por lo que ya\(G\) es un árbol.
Ahora supongamos que\(G\) tiene\(m\ge1\) bordes. Si\(G\) es un árbol, es su propio árbol que abarca. De lo contrario,\(G\) contiene un ciclo; eliminar un borde de este ciclo. El gráfico resultante todavía\(G'\) está conectado y tiene menos bordes, por lo que tiene un árbol de expansión; este también es un árbol de expansión para\(G\).
En general, los árboles de expansión no son únicos, es decir, una gráfica puede tener muchos árboles de expansión. Es posible que algunos bordes estén en cada árbol de expansión incluso si hay múltiples árboles de expansión. Por ejemplo, cualquier borde colgante debe estar en cada árbol de expansión, al igual que cualquier borde cuya eliminación desconecte la gráfica (tal borde se llama puente).
Corolario \(\PageIndex{1}\)
Si\(G\) está conectado, tiene al menos\(n-1\) bordes; además, tiene exactamente\(n-1\) bordes si y solo si es un árbol.
- Prueba
-
Si\(G\) está conectado, tiene un árbol de expansión, que tiene\(n-1\) bordes, todos los cuales son bordes de\(G\).
Si\(G\) tiene\(n-1\) bordes, que deben ser los bordes de su árbol de expansión, entonces\(G\) es un árbol.
Teorema \(\PageIndex{6}\)
\(G\)es un árbol si y sólo si hay un camino único entre dos vértices cualesquiera.
- Prueba
-
si: Dado que cada dos vértices están conectados por una ruta,\(G\) está conectado. Para una contradicción, supongamos que hay un ciclo adentro\(G\); entonces dos vértices cualesquiera en el ciclo están conectados por al menos dos caminos distintos, una contradicción.
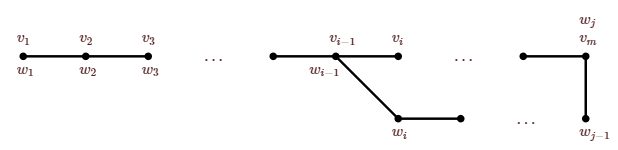
solo si: Si\(G\) es un árbol está conectado, por lo que entre dos vértices cualesquiera hay al menos un camino. Para una contradicción, supongamos que hay dos caminos diferentes de\(v\) a\(w\):\[v=v_1,v_2,\ldots,v_k=w \quad\hbox{and}\quad v=w_1,w_2,\ldots,w_l=w.\nonumber\] Let\(i\) be the smaller integer such that\(v_i\not= w_i\). Entonces deja\(j\) ser el entero más pequeño mayor o igual que\(i\) tal que\(w_j=v_m\) para algunos\(m\), que debe ser al menos\(i\). (Ya que\(w_l=v_k\), tal\(m\) debe existir.) Entonces\(v_{i-1},v_i,\ldots,v_m=w_j,w_{j-1},\ldots,w_{i-1}=v_{i-1}\) es un ciclo de entrada\(G\), una contradicción. Ver Figura\(\PageIndex{1}\).
Definición\(\PageIndex{4}\): Cutpoint
Un punto de corte en una gráfica conectada\(G\) es un vértice cuya eliminación desconecta la gráfica.
Teorema \(\PageIndex{7}\)
Cada gráfica conectada tiene un vértice que no es un punto de corte.
- Prueba
-
Retire un vértice colgante en un árbol de expansión para la gráfica.


