5.10: Colorear Gráficas Planares
- Page ID
- 117084
Ahora volvemos al problema original de coloración gráfica: colorear mapas. Como se indica en la Sección 1.2, el problema de coloración del mapa puede convertirse en un problema de coloración gráfica. En la figura se\(\PageIndex{1}\) muestra el ejemplo de la Sección 1.2.
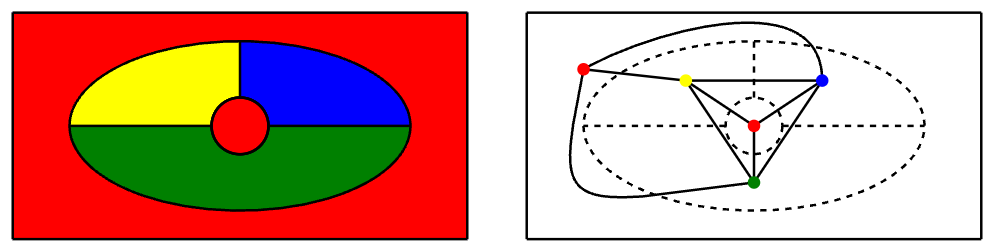
Las gráficas formadas a partir de mapas de esta manera tienen una propiedad importante: son planas.
Definición\(\PageIndex{1}\): Planar
Una gráfica\(G\) es plana si se puede representar mediante un dibujo en el plano para que no se crucen aristas.
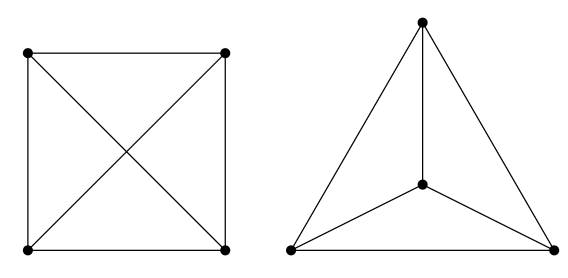
Tenga en cuenta que esta definición solo requiere que alguna representación de la gráfica no tenga bordes cruzados. La figura\(\PageIndex{2}\) muestra dos representaciones de\(K_4\); ya que en la segunda no hay bordes cruzados,\(K_4\) es plana.
El número de colores necesarios para colorear correctamente cualquier mapa es ahora el número de colores necesarios para colorear cualquier gráfico plano. Este problema se planteó por primera vez en el siglo XIX, y rápidamente se conjeturó que en todos los casos bastaban con cuatro colores. Esto finalmente se demostró en 1976 (ver Figura\(\PageIndex{3}\)) con la ayuda de una computadora. En 1879, Alfred Kempe dio una prueba que era ampliamente conocida, pero que era incorrecta, aunque no fue hasta 1890 que esto fue notado por Percy Heawood, quien modificó la prueba para mostrar que cinco colores bastan para colorear cualquier gráfica plana. Vamos a probar este Teorema de Cinco Colores, pero primero necesitamos algunos otros resultados. Asumimos que todas las gráficas son simples.

Teorema \(\PageIndex{1}\): Euler's Formula
Supongamos que\(G\) es una gráfica plana conectada, dibujada de manera que no se crucen aristas, con\(n\) vértices y\(m\) aristas, y que la gráfica divida el plano en\(r\) regiones. Entonces\[r=m-n+2.\nonumber\]
- Prueba
-
La prueba es por inducción en el número de aristas. El caso base es\(m=n-1\), el número mínimo de aristas en una gráfica conectada en\(n\) vértices. En este caso\(G\) es un árbol, y no contiene ciclos, por lo que el número de regiones es 1, y de hecho\(1=(n-1)-n+2\).
Ahora supongamos que\(G\) tiene más que\(n-1\) bordes, por lo que tiene un ciclo. Elimine un borde de un ciclo de formación\(G'\), que está conectado y tiene\(r-1\) regiones,\(n\) vértices y\(m-1\) aristas. Por la hipótesis de inducción\(r-1=(m-1)-n+2\), que se convierte\(r=m-n+2\) cuando sumamos 1 a cada lado.
Lema \(\PageIndex{1}\)
Supongamos que\(G\) es una gráfica plana simple conectada, dibujada de manera que no se crucen aristas, con\(n\ge3\) vértices y\(m\) aristas, y que la gráfica divida el plano en\(r\) regiones. Entonces\(m\le 3n-6\).
- Prueba
-
\(f_i\)Sea el número de aristas que colindan con el número de región\(i\); si la misma región está en ambos lados de una arista, esa arista se cuenta dos veces. Llamamos a los bordes adyacentes a una región los bordes de límite de la región. Ya que\(G\) es simple y\(n\ge3\), cada región está delimitada por al menos 3 bordes. Entonces\(\sum_{i=1}^r f_i=2m\), ya que cada borde se cuenta dos veces, una para la región a cada lado del borde. De\(r=m-n+2\) nosotros obtenemos\(3r=3m-3n+6\), y porque\(f_i\ge 3\),\(3r\le \sum_{i=1}^r f_i=2m\), así\(3m-3n+6\le 2m\), o\(m\le 3n-6\) como se desee.
Teorema \(\PageIndex{2}\)
\(K_5\)no es plano.
- Prueba
-
\(K_5\)tiene 5 vértices y 10 aristas, y\(10\not\le 3\cdot 5-6\), así por el lema, no\(K_5\) es plano.
Lema \(\PageIndex{2}\)
Si\(G\) es plano entonces\(G\) tiene un vértice de grado como máximo 5.
- Prueba
-
Supongamos que\(\text{d}(v_i)>5\) para todos\(v_i\). Entonces\(2m=\sum_{i=1}^n \text{d}(v_i)\ge 6n\). Por Lemma\(\PageIndex{1}\),\(3n-6\ge m\) entonces\(6n-12\ge 2m\). Así\(6n\le 2m \le 6n-12\), una contradicción.
Teorema \(\PageIndex{3}\): Five Color Theorem
Cada gráfico plano puede ser coloreado con 5 colores.
- Prueba
-
La prueba es por inducción en el número de vértices\(n\); cuando\(n\le 5\) esto es trivial.
Ahora supongamos que\(G\) es plano en más de 5 vértices; por Lemma\(\PageIndex{2}\) algún vértice\(v\) tiene grado como máximo 5. Por la hipótesis de inducción, se\(G-v\) puede colorear con 5 colores. Colorea los vértices de\(G\), que no sean\(v\), ya que están coloreados en un 5 colores de\(G-v\). Si\(\text{d}(v)\le 4\), entonces se\(v\) puede colorear con uno de los 5 colores para dar una coloración adecuada de\(G\) con 5 colores. Entonces ahora suponemos\(\text{d}(v)=5\). Si los cinco vecinos de\(v\) están coloreados con cuatro o menos de los colores, entonces nuevamente se\(v\) pueden colorear para dar una coloración adecuada de\(G\) con 5 colores.
Ahora suponemos que los cinco vecinos de\(v\) tienen un color diferente, como se indica en la Figura\(\PageIndex{4}\).
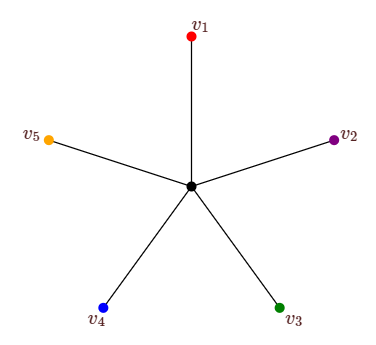
Figura\(\PageIndex{4}\): Cinco vecinos de\(v\) color con 5 colores:\(v_1\) es rojo,\(v_2\) es morado,\(v_3\) es verde,\(v_4\) es azul,\(v_5\) es naranja. Supongamos que en\(G\) hay un camino de\(v_1\) a\(v_3\), y que los vértices a lo largo de este camino son alternativamente coloreados de rojo y verde; llamar a dicho camino camino un camino alterno rojo-verde. Entonces junto con\(v\), este camino hace un ciclo con\(v_2\) por dentro y\(v_4\) por fuera, o viceversa. Esto significa que no puede haber un camino alterno de color púrpura azul de\(v_2\) a\(v_4\). Suponiendo que\(v_2\) está dentro del ciclo, cambiamos los colores de todos los vértices dentro del ciclo de color púrpura a azul, y todos los vértices azules se vuelven a colorear púrpura. Esta sigue siendo una coloración adecuada de todos los vértices de\(G\) excepto\(v\), y ahora ningún vecino de\(v\) es púrpura, por lo que al colorear\(v\) púrpura obtenemos una coloración adecuada de\(G\).
Si no hay un camino alterno rojo-verde de\(v_1\) a\(v_3\), entonces volvemos a colorear los vértices de la siguiente manera: Cambiar el color de\(v_1\) a verde. Cambiar todos los vecinos verdes de\(v_1\) a rojo. Continuar cambiando los colores de los vértices de rojo a verde o verde a rojo hasta que no haya conflictos, es decir, hasta que se obtenga una nueva coloración adecuada. Debido a que no hay camino alterno rojo-verde de\(v_1\) a\(v_3\), el color de no\(v_3\) cambiará. Ahora ningún vecino de\(v\) es de color rojo, así que coloreando\(v\) rojo obtenemos una coloración adecuada de\(G\).


