5.E: Teoría de las Gráficas (Ejercicios)
- Page ID
- 117092
5.1: Fundamentos
Ejercicio\(\PageIndex{1.1}\)
El complemento\(\overline G\) de la gráfica simple\(G\) es una gráfica simple con los mismos vértices que\(G\), y\(\{v,w\}\) es un borde de\(\overline G\) si y sólo si no es un borde de\(G\). Una gráfica\(G\) es autocomplementaria si\(G\cong \overline G\). Mostrar que si\(G\) es autocomplementario entonces tiene\(4k\) o\(4k+1\) vértices para algunos\(k\). Encuentra gráficas autocomplementarias en 4 y 5 vértices.
Ejercicio\(\PageIndex{1.2}\)
Demostrar que si\(\sum_{i=1}^n d_i\) es par, hay una gráfica (no necesariamente simple) con secuencia de grados\(d_1,d_2,\ldots,d_n\).
Ejercicio\(\PageIndex{1.3}\)
Supongamos\(d_1\ge d_2\ge\cdots\ge d_n\) y\(\sum_{i=1}^n d_i\) es parejo. Demostrar que hay un multígrafo con secuencia de grados\(d_1,d_2,\ldots,d_n\) si y solo si\(d_1\le \sum_{i=2}^n d_i\).
Ejercicio\(\PageIndex{1.4}\)
Demostrar que no\(0,1,2,3,4\) es gráfico.
Ejercicio\(\PageIndex{1.5}\)
¿Es\(4,4,3,2,2,1,1\) gráfico? Si no, explica por qué; si es así, encuentra una gráfica simple con esta secuencia de grados.
Ejercicio\(\PageIndex{1.6}\)
¿Es\(4,4,4,2,2\) gráfico? Si no, explica por qué, y encuentra una gráfica con esta secuencia de grados; si es así, encuentra una gráfica simple con esta secuencia de grados.
Ejercicio\(\PageIndex{1.7}\)
Demostrar que una gráfica simple con\(n\ge 2\) vértices tiene dos vértices del mismo grado.
Ejercicio\(\PageIndex{1.8}\)
Demostrar la parte “sólo si” del Teorema 5.1.2.
Ejercicio\(\PageIndex{1.9}\)
Demostrar que la condición sobre los grados en Teorema 5.1.2 es equivalente a esta condición:\(\sum_{i=1}^n d_i\) es par y para todos\(k\in \{1,2,\ldots,n\}\), y todos\(\{i_1,i_2,\ldots, i_k\}\subseteq [n]\),\[\sum_{j=1}^k d_{i_j}\le k(k-1)+ \sum_{i\notin \{i_1,i_2,\ldots, i_k\}} \min(d_i,k).\nonumber\] No usar Teorema 5.1.2.
Ejercicio\(\PageIndex{1.10}\)
Dibuja las 11 gráficas no isomórficas con cuatro vértices.
Ejercicio\(\PageIndex{1.11}\)
Supongamos\(G_1\cong G_2\). Mostrar que si\(G_1\) contiene un ciclo de duración\(k\) también lo hace\(G_2\).
Ejercicio\(\PageIndex{1.12}\)
Definir\(v\sim w\) si y sólo si hay una ruta conectando vértices\(v\) y\(w\). Demostrar que\(\sim\) es una relación de equivalencia.
Ejercicio\(\PageIndex{1.13}\)
Demostrar la parte “si” del Teorema 5.1.2, de la siguiente manera:
La prueba es por inducción en\(s=\sum_{i=1}^n d_i\). Esto es fácil de ver si\(s=2\), así que supongamos\(s>2\). Sin pérdida de generalidad podemos suponer eso\(d_n>0\). Dejar\(t\) ser el menor entero tal que\(d_t>d_{t+1}\), o\(t=n-1\) si no hay tal entero. Vamos\(d_t'=d_t-1\),\(d_n'=d_n-1\), y\(d_i'=d_i\) para todos los demás\(i\). Tenga en cuenta que\(d_1'\ge d_2'\ge\cdots d_n'\). Queremos demostrar que la secuencia\(\{d_i'\}\) satisface la condición del teorema, es decir, que para todos\(k\in \{1,2,\ldots,n\}\),\[\sum_{i=1}^k d_i'\le k(k-1)+\sum_{i=k+1}^n \min(d_i',k).\nonumber\] hay cinco casos:
- \(k\ge t\)
- \(k< t\),\(d_k< k\)
- \(k< t\),\(d_k=k\)
- \(k< t\),\(d_n>k\)
- \(k< t\),\(d_k > k\),\(d_n\le k\)
Por la hipótesis de inducción, existe una gráfica simple con secuencia de grados\(\{d_i'\}\). Por último, mostrar que existe una gráfica con secuencia de grados\(\{d_i\}\).
Esta prueba se debe a S. A. Choudum, A Simple Proof of the Erdős-Gallai Theorema on Graph Sequence, Bulletin of the Australian Mathematics Society, vol. 33, 1986, pp. 67-70. La prueba de Paul Erdős y Tibor Gallai fue larga; Berge proporcionó una prueba más corta que utilizó resultados en la teoría de los flujos de red. La prueba de Choudum es a la vez corta y elemental.
5.2: Euler Circuitos y Paseos
Ejercicio\(\PageIndex{2.1}\)
Supongamos que una gráfica conectada\(G\) tiene secuencia de grados\(d_1,d_2,\ldots,d_n\). ¿A cuántos bordes hay que añadir para\(G\) que la gráfica resultante tenga un circuito de Euler? Explique.
Ejercicio\(\PageIndex{2.2}\)
¿Cuáles gráficas completas\(K_n\),\(n\ge 2\), tienen circuitos de Euler? ¿Cuáles tienen paseos de Euler? Justifica tus respuestas.
Ejercicio\(\PageIndex{2.3}\)
Demostrar que si los vértices\(v\) y\(w\) están unidos por un paseo están unidos por un camino.
Ejercicio\(\PageIndex{2.4}\)
Mostrar que si\(G\) está conectado y tiene exactamente\(2k\) vértices de grado impar,\(k\ge1\), sus bordes se pueden particionar en\(k\) paseos. ¿Es esto cierto para los no conectados\(G\)?
5.3: Ciclos y caminos de Hamilton
Ejercicio\(\PageIndex{3.1}\)
Supongamos que una gráfica simple\(G\) sobre\(n\) vértices tiene al menos\( {(n-1)(n-2)\over2}+2\) aristas. Demostrar que\(G\) tiene un ciclo Hamilton. Para\(n\ge 2\), mostrar que hay una gráfica simple con\( {(n-1)(n-2)\over2}+1\) bordes que no tiene ciclo Hamilton.
Ejercicio\(\PageIndex{3.2}\)
Demostrar Teorema 5.3.2.
Ejercicio\(\PageIndex{3.3}\)
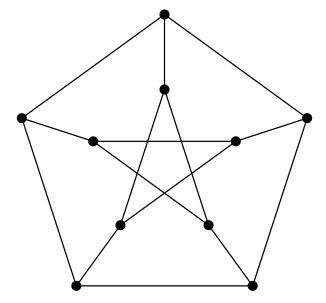
La gráfica que se muestra a continuación es la gráfica de Petersen. ¿Tiene un ciclo Hamilton? Justifica tu respuesta. ¿Tiene un camino Hamilton? Justifica tu respuesta.
5.4: Gráficas bipartitas
Ejercicio\(\PageIndex{4.1}\)
Demostrar que existe un multígrafo bipartito con secuencia de grados\(d_1,\ldots,d_n\) si y sólo si hay una partición\(\{I,J\}\) de\([n]\) tal manera que\[\sum_{i\in I}d_i=\sum_{i\in J} d_i.\nonumber\]
Ejercicio\(\PageIndex{4.2}\)
¿Cuál es el menor número de aristas que se pueden eliminar\(K_5\) para crear una gráfica bipartita?
Ejercicio\(\PageIndex{4.3}\)
Una gráfica regular es aquella en la que el grado de cada vértice es el mismo. Mostrar que si\(G\) es una gráfica bipartita regular, y el grado común de los vértices es de al menos 1, entonces las dos partes son del mismo tamaño.
Ejercicio\(\PageIndex{4.4}\)
Una coincidencia perfecta es aquella en la que todos los vértices de la gráfica son incidentes con un borde en la coincidencia. Demostrar que una gráfica bipartita regular con grado común al menos 1 tiene una coincidencia perfecta. (Discutimos los emparejamientos en la Sección 4.6.)
5.5: Árboles
Ejercicio\(\PageIndex{5.1}\)
Supongamos que\(G\) es una gráfica conectada, y que cada árbol de expansión contiene borde\(e\). Demostrar que\(e\) es un puente.
Ejercicio\(\PageIndex{5.2}\)
Demuestre que cada borde de un árbol es un puente.
Ejercicio\(\PageIndex{5.3}\)
Mostrar que\(G\) es un árbol si y solo si no tiene ciclos y agregar cualquier borde nuevo crea una gráfica con exactamente un ciclo.
Ejercicio\(\PageIndex{5.4}\)
¿Qué árboles tienen paseos Euler?
Ejercicio\(\PageIndex{5.5}\)
¿Qué árboles tienen caminos Hamilton?
Ejercicio\(\PageIndex{5.6}\)
Vamos\(n\ge 2\). Demostrar que hay un árbol con secuencia de grados\(d_1,d_2,\ldots,d_n\) si y solo si\(d_i>0\) para todos\(i\) y\(\sum_{i=1}^n d_i=2(n-1)\).
Ejercicio\(\PageIndex{5.7}\)
Un multiárbol es un multígrafo cuya condensación es un árbol. Vamos\(n\ge 2\). Dejar\(d_1,d_2,\ldots,d_n\) ser enteros positivos, y dejar que\(g\) sea el mayor divisor común de la\(d_i\). Demostrar que hay un multiárbol con secuencia de grados\(d_1,d_2,\ldots,d_n\) si y solo si\(\sum_{i=1}^n d_i/g\ge 2(n-1)\) y para alguna partición\(I\),\(J\) de\([n]\),\(\sum_{i\in I}d_i=\sum_{i\in J} d_i\).
Ejercicio\(\PageIndex{5.8}\)
Supongamos que\(T\) es un árbol sobre\(n\) vértices,\(k\) de los cuales tienen grado mayor que\(1,\: d_1,\: d_2,\cdots d_k\). Por supuesto, también\(T\) deben tener vértices colgantes. ¿Cuántos vértices colgantes? Tu respuesta debe depender únicamente de\(k\) y\(d_1,\: d_2,\cdots d_k\).
5.6: Árboles de expansión óptimos
Ejercicio\(\PageIndex{6.1}\)
El algoritmo de Kruskal también es un algoritmo codicioso que produce un árbol de expansión de costo mínimo para una gráfica conectada\(G\). Comience por elegir una ventaja en\(G\) el menor costo. Suponiendo que se\(e_1, e_2,\ldots,e_i\) hayan elegido aristas, elija una arista\(e_{i+1}\) que no forme un ciclo junto con\(e_1, e_2,\ldots,e_i\) y que tenga el menor costo entre todas esas aristas. Los bordes\(e_1, e_2,\ldots,e_{n-1}\) forman un árbol de expansión para\(G\). Demuestre que este árbol de expansión tiene un costo mínimo.
Ejercicio\(\PageIndex{6.2}\)
Demuestre que si los costos de borde de\(G\) son distintos, hay exactamente un árbol de expansión de costos mínimos. Dé un ejemplo de una gráfica\(G\) con más de un árbol de expansión de costo mínimo.
Ejercicio\(\PageIndex{6.3}\)
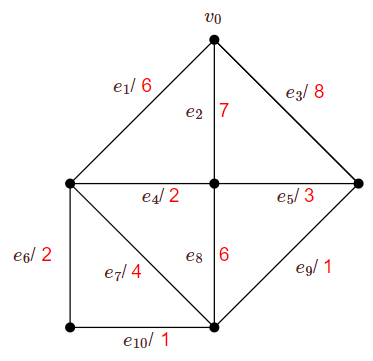
Tanto en los algoritmos Jarník como en Kruskal, puede ser que se puedan agregar dos o más bordes en cualquier paso en particular, y se requiere algún método para elegir uno sobre el otro. Para la gráfica a continuación, use ambos algoritmos para encontrar un árbol de expansión de costos mínimos. Usando las etiquetas\(e_i\) en la gráfica, en cada etapa escoge el borde\(e_i\) que el algoritmo especifica y que tiene el menor posible\(i\) entre todos los bordes disponibles. Para el algoritmo Jarník, utilice el designado\(v_0\) como vértice inicial. Para cada algoritmo, enumere los bordes en el orden en que se agreguen. Los pesos de borde\(e_1,e_2,\ldots,e_{10}\) son\(6,7,8,2,3,2,4,6,1,1\).
5.7: Conectividad
Ejercicio\(\PageIndex{7.1}\)
Supongamos que una gráfica simple\(G\) sobre\(n\ge 2\) vértices tiene al menos\( {(n-1)(n-2)\over2}+1\) aristas. Demostrar que\(G\) está conectado.
Ejercicio\(\PageIndex{7.2}\)
Supongamos que una gráfica general\(G\) tiene exactamente dos vértices de grado impar,\(v\) y\(w\). Dejar\(G'\) ser la gráfica creada mediante la adición de una unión de borde\(v\) a\(w\). Demostrar que\(G'\) está conectado si y solo si\(G\) está conectado.
Ejercicio\(\PageIndex{7.3}\)
Supongamos que\(G\) es simple con secuencia de grados\(d_1\le d_2\le\cdots\le d_n\), y para\(k\le n-d_n-1\),\(d_k\ge k\). \(G\)El show está conectado.
Ejercicio\(\PageIndex{7.4}\)
Recordemos que una gráfica es\(k\) -regular si todos los vértices tienen grado\(k\). Cuál es el entero más pequeño\(k\) que hace que esto sea cierto:
Si\(G\) es simple, tiene\(n\) vértices,\(m\ge k\), y\(G\) es\(m\) -regular, entonces\(G\) está conectado.
(Por supuesto\(k\) depende de\(n\).)
Ejercicio\(\PageIndex{7.5}\)
Supongamos que\(G\) tiene al menos un borde. Mostrar que\(G\) es 2-conectado si y sólo si para todos los vértices\(v\) y aristas\(e\) hay un ciclo que contiene\(v\) y\(e\).
Ejercicio\(\PageIndex{7.6}\)
Encuentra una gráfica sencilla con\(\kappa(G)< \lambda(G)< \delta(G)\).
Ejercicio\(\PageIndex{7.7}\)
Supongamos\(\lambda(G)=k>0\). Mostrar que hay conjuntos de vértices\(U\) y\(V\) que particiona los vértices de\(G\), y tal que hay exactamente\(k\) bordes con un punto final adentro\(U\) y un punto final adentro\(V\).
Ejercicio\(\PageIndex{7.8}\)
Encontrar\(\lambda(K_{m,n})\), donde ambos\(m\) y\(n\) son por lo menos 1.
Ejercicio\(\PageIndex{7.9}\)
Supongamos que\(G\) es una gráfica conectada. El gráfico bloque de punto de corte de\(G\),\(BC(G)\) se forma de la siguiente manera: Que los vértices\(c_1,c_2,\ldots,c_k\) sean los puntos de corte de\(G\), y dejar que los bloques de\(G\) ser\(B_1,\ldots,B_l\). Los vértices de\(BC(G)\) son\(c_1,…,c_k,B_1,\ldots,B_l\). Agrega un borde\(\{B_i,c_j\}\) si y solo si\(c_j\in B_i\). Mostrar que la gráfica de bloque de punto de corte es un árbol.
Tenga en cuenta que un punto de corte está contenido en al menos dos bloques, de modo que todos los vértices colgantes del gráfico de punto de corte de bloques son bloques. Estos bloques se llaman bloques finales.
Ejercicio\(\PageIndex{7.10}\)
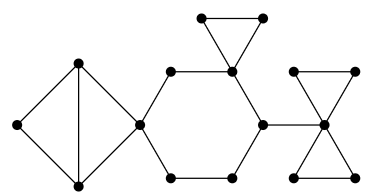
Dibuja la gráfica de bloques-punto de corte de la gráfica de abajo.
Ejercicio\(\PageIndex{7.11}\)
Mostrar que el complemento de una gráfica desconectada está conectado. ¿El complemento de una gráfica conectada siempre está desconectado? (El complemento\(\overline G\) de gráfico\(G\) tiene los mismos vértices que\(G\), y\(\{v,w\}\) es un borde de\(\overline G\) si y solo si no es un borde de\(G\).)
5.8: Colorear Gráfica
Ejercicio\(\PageIndex{8.1}\)
Supongamos que\(G\) tiene\(n\) vértices y número cromático\(k\). Demostrar que\(G\) tiene al menos\(k\choose2\) bordes.
Ejercicio\(\PageIndex{8.2}\)
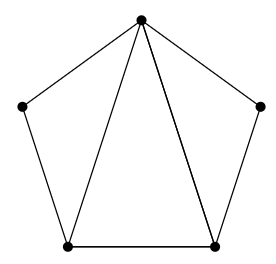
Encuentra el número cromático de la gráfica a continuación usando el algoritmo en esta sección. Dibuja todas las gráficas\(G+e\) y\(G/e\) generadas por el alorithm en una “estructura de árbol” con las gráficas completas en la parte inferior, etiquete cada gráfica completa con su número cromático, luego proponga los valores hasta la gráfica original.
Ejercicio\(\PageIndex{8.3}\)
Mostrar que una gráfica es bipartita si y sólo si se puede colorear correctamente con dos colores.
Ejercicio\(\PageIndex{8.4}\)
Demostrar que\(\chi(G-v)\) es\(\chi(G)\) o\(\chi(G)-1\).
Ejercicio\(\PageIndex{8.5}\)
Demostrar Teorema 5.8.3 sin asumir ninguna propiedad particular del orden\(v_1,\ldots,v_n\).
Ejercicio\(\PageIndex{8.6}\)
Demostrar Teorema 5.8.4 de la siguiente manera. Por Corolario 5.8.1 necesitamos considerar solo gráficas regulares. Las gráficas regulares de grado 2 son fáciles, por lo que consideramos solo gráficas regulares de grado al menos 3.
Si no\(G\) es 2-conectado, mostrar que los bloques de\(G\) pueden colorearse con\(\Delta(G)\) colores, y luego los colorantes pueden ser alterados ligeramente para que se combinen para dar una coloración adecuada de\(G\).
Si\(G\) es 2-conectado, mostrar que hay vértices\(u\),\(v\),\(w\) tal que\(u\) es adyacente a ambos\(v\) y\(w\),\(v\) y no\(w\) son adyacentes, y\(G-v-w\) está conectado. Dados tales vértices, color\(v\) y\(w\) con color 1, luego colorea los vértices restantes por un algoritmo codicioso similar al del Teorema 5.8.4, con\(u\) jugar el papel de\(v_n\).
Para mostrar la existencia de\(u\)\(v\),\(w\) según sea necesario, dejar\(x\) ser un vértice no adyacente a todos los demás vértices. Si\(G-x\) es 2-conectado, let\(v=x\), let\(w\) be at distance 2 from\(v\) (justifique esto), y deje que un camino de longitud 2 sea\(v,u,w\). Utilice el Teorema 5.7.2 para demostrar que\(u\)\(v\),,\(w\) tienen las propiedades requeridas.
Si no\(G-x\) es 2-conectado, let\(u=x\) y let\(v\) y\(w\) ser (cuidadosamente elegido) vértices en dos bloques finales diferentes de\(G-x\). Demostrar que\(u\)\(v\),,\(w\) tener las propiedades requeridas.
Brooks probó el teorema en 1941; esta prueba más simple se debe a Lovász, 1975.
5.9: El polinomio cromático
Ejercicio\(\PageIndex{9.1}\)
Demostrar que el coeficiente principal de\(P_G\) es 1.
Ejercicio\(\PageIndex{9.2}\)
Supongamos que no\(G\) está conectado y tiene componentes\(C_1,\ldots,C_k\). \(P_G=\prod_{i=1}^k P_{C_i}\)Demuéstralo.
Ejercicio\(\PageIndex{9.3}\)
Demostrar que el término constante de\(P_G(k)\) es 0. Mostrar que el coeficiente de\(k\) in\(P_G(k)\) es distinto de cero si y solo si\(G\) está conectado.
Ejercicio\(\PageIndex{9.4}\)
Mostrar que el coeficiente de\(k^{n-1}\) in\(P_G\) es\(-1\) multiplicado por el número de aristas en\(G\).
Ejercicio\(\PageIndex{9.5}\)
Demostrar que\(G\) es un árbol si y solo si\(P_G(k)=k(k-1)^{n-1}\).
Ejercicio\(\PageIndex{9.6}\)
Encuentra el polinomio cromático de\(K_n\) con un borde eliminado.
5.10: Colorear Gráficas Planares
Ejercicio\(\PageIndex{10.1}\)
\(K_{3,3}\)El espectáculo no es plano. (Prueba un lema como Lema 5.10.1 para gráficas bipartitas, luego haz algo así como la prueba del Teorema 5.10.2.) ¿Cuál es el número cromático de\(K_{3,3}\)?
5.11: Gráficas dirigidas
Ejercicio\(\PageIndex{11.1}\)
La conectividad en dígrafos resulta ser un poco más complicada que la conectividad en las gráficas. Un dígrafo está conectado si el gráfico subyacente está conectado. (La gráfica subyacente de un dígrafo se produce eliminando la orientación de los arcos para producir aristas, es decir, reemplazando cada arco\((v,w)\) por una arista\(\{v,w\}\). Incluso si el dígrafo es simple, el gráfico subyacente puede tener múltiples bordes). Un dígrafo está fuertemente conectado si por cada vértices\(v\) y\(w\) hay un paseo de\(v\) a\(w\). Dé un ejemplo de un dígrafo que está conectado pero no fuertemente conectado.
Ejercicio\(\PageIndex{11.2}\)
Un dígrafo tiene un circuito de Euler si hay un paseo cerrado que usa cada arco exactamente una vez. Mostrar que un dígrafo sin vértices de grado 0 tiene un circuito de Euler si y sólo si está conectado y\(\text{d}^+(v)=\text{d}^-(v)\) para todos los vértices\(v\).
Ejercicio\(\PageIndex{11.3}\)
Un torneo es una gráfica completa orientada. Es decir, se trata de un dígrafo sobre\(n\) vértices, que contiene exactamente uno de los arcos\((v,w)\) y\((w,v)\) por cada par de vértices. Un camino de Hamilton es un paseo que usa cada vértice exactamente una vez. Demuestre que cada torneo tiene un camino Hamilton.
Ejercicio\(\PageIndex{11.4}\)
Interpreta un torneo de la siguiente manera: los vértices son jugadores. Si\((v,w)\) es un arco, el jugador\(v\) venció\(w\). Decir que\(v\) es un campeón si por cada otro jugador\(w\), ya sea\(v\) vencer\(w\) o\(v\) vencer a un jugador que venció\(w\). Demuestre que un jugador con el número máximo de victorias es campeón. Encuentra un torneo de 5 vértices en el que cada jugador sea campeón.


