6.5: Operaciones de Cierre en Relaciones

En la Sección 6.1, estudiamos las relaciones y una operación importante sobre las relaciones, a saber, la composición. Esta operación nos permite generar nuevas relaciones a partir de relaciones previamente conocidas. En la Sección 6.3, discutimos algunas propiedades clave de las relaciones. Ahora queremos considerar la situación de construir una nueva relación a\(r^+\) partir de una relación existente\(r\) donde, primero,\(r^+\) contiene\(r\) y, segundo,\(r^{+ }\) satisface la propiedad transitiva.

Cierre Transitivo

Considerar una red telefónica en la que la oficina principal\(a\) esté conectada a, y pueda comunicarse con, individuos\(b\) y\(c\text{.}\) Ambos\(b\) y\(c\) pueda comunicarse con otra persona,\(d\text{;}\) sin embargo, la oficina principal no puede comunicarse con\(d\text{.}\) Asumir la comunicación es sólo de una manera, como se indica. Esta situación puede ser descrita por la relación\(r = \{(a, b), (a, c), (b, d), (c, d)\}\text{.}\) Nos gustaría cambiar el sistema para que la oficina principal\(a\) pueda comunicarse con la persona\(d\) y aún así mantener el sistema anterior. Nosotros, por supuesto, queremos el sistema más económico.

Esto se puede reformular de la siguiente manera; Encontrar la relación más pequeña\(r^{+ }\) que contiene\(r\) como subconjunto y que es transitiva;\(r^+ =\{(a, b), (a, c), (b, d), (c, d), (a, d)\}\text{.}\)

Definición \(\PageIndex{1}\): Transitive Closure

Dejar\(A\) ser un conjunto y\(r\) ser una relación en\(A\text{.}\) El cierre transitivo de\(r\text{,}\) denotado por\(r^+\text{,}\) es la relación transitiva más pequeña que contiene\(r\) como subconjunto.

Dejar\(A = \{1, 2, 3, 4\}\text{,}\) y dejar\(\mathcal{S} = \{(1, 2), (2, 3), (3, 4)\}\) ser una relación sobre\(A\text{.}\) Esta relación se llama la relación sucesora en\(A\) ya que cada elemento está relacionado con su sucesor. Cómo calculamos\(\mathcal{S}^+\text{?}\) Por inspección observamos que\((1, 3)\) debe estar en\(\mathcal{S}^+\). Analicemos por qué. Esto es así porque\((1,2) \in \mathcal{S}\) y\((2, 3) \in \mathcal{S}\text{,}\) y la propiedad transitiva obliga\((1,3)\) a estar en\(\mathcal{S}^+\text{.}\)

En general, se deduce que si\((a, b) \in \mathcal{S}\) y\((b, c) \in S,\) entonces\((a, c) \in \mathcal{S}^+ \text{.}\) Esta condición es exactamente el requisito de membresía para que el par\((a, c)\) esté en la composición\(\mathcal{S}\mathcal{S} = \mathcal{S}^2\text{.}\) Así que cada elemento en\(\mathcal{S}^2\) debe ser un elemento en\(\mathcal{S}^+\). Entonces ahora sabemos eso,\(\mathcal{S}^+\) contiene por lo menos\(\mathcal{S} \cup \mathcal{S}^2\). En particular, para este ejemplo, desde\(\mathcal{S} = \{(1, 2), (2, 3), (3, 4)\}\) y\(\mathcal{S}^2 = \{(1, 3), (2, 4)\}\text{,}\) tenemos

\ begin {ecuación*}\ mathcal {S}\ copa\ mathcal {S} ^2 =\ {(1, 2), (2, 3), (3, 4), (1, 3), (2, 4)\}\ end {ecuación*}

¿La relación es\(\mathcal{S} \cup \mathcal{S}^2\) transitiva? Nuevamente, por inspección, no\((1, 4)\) es un elemento de\(\mathcal{S} \cup \mathcal{S}^2\text{,}\) sino\((1,3) \in \mathcal{S}^2\) y\((3, 4) \in \mathcal{S}\text{.}\) Por lo tanto, la composición\(\mathcal{S}^2 \mathcal{S} = \mathcal{S}^3\) produce\((1, 4)\text{,}\) y debe ser un elemento de\(\mathcal{S}^+\) ya\((1,3)\) y\((3, 4)\) se requiere estar en\(\mathcal{S}^+\text{.}\) Esto demuestra que\(\mathcal{S}^3 \subseteq \mathcal{S}^+\text{.}\) Este proceso debe continuarse hasta que la relación resultante sea transitiva. Si\(A\) es finito, como es cierto en este ejemplo, el cierre transitivo se obtendrá en un número finito de pasos. Para este ejemplo,

\ begin {ecuación*}\ mathcal {S} ^+ =\ mathcal {S}\ copa\ mathcal {S} ^2\ copa\ mathcal {S} ^3=\ {(1, 2), (2, 3), (3, 4), (1, 3), (2, 4), (1,4)\}\ end {ecuación*}

Teorema\(\PageIndex{1}\): Transitive Closure on a Finite Set

Si\(r\) es una relación sobre un conjunto\(A\) y\(\lvert A \rvert = n\text{,}\) entonces el cierre transitivo de\(r\) es la unión de los primeros\(n\) poderes de r.

\ begin {ecuación*} r^+ = r\ taza r^2\ taza r ^3\ taza\ cdots\ taza r^n\ texto {.} \ end {ecuación*}

Consideremos ahora el análogo matricial del cierre transitivo.

Considerar la relación

\ begin {ecuación*} r =\ {(1, 4), (2, 1), (2, 2), (2, 3), (3, 2), (4, 3), (4, 5), (5, 1)\}\ end {ecuación*}

en el set\(A = \{1,2, 3, 4, 5\}\text{.}\) La matriz de\(r\) es

\ begin {ecuación*} R=\ left (\ begin {array} {ccccc} 0 & 0 & 0 & 1 & 0\\ 1 & 1 & 1 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ end {array}\ derecha)\ end {ecuación*}

Recordemos que se\(r^2, r^3, \ldots\) puede determinar mediante la computación de las potencias de la matriz\(R^2, R^3, \ldots\text{.}\) Para nuestro ejemplo,

Mesa\(\PageIndex{1}\)

\(R^2=\left( \begin{array}{ccccc} 0 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ \end{array} \right)\)	\(R^3=\left( \begin{array}{ccccc} 1 & 1 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 \\ 0 & 0 & 1 & 0 & 1 \\ \end{array} \right)\)
\(R^4=\left( \begin{array}{ccccc} 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 0 & 0 \\ \end{array} \right)\)	\(R^5=\left( \begin{array}{ccccc} 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 0 \\ \end{array} \right)\)

¿Cómo nos relacionamos\(\underset{i=1}{\overset{5}{\cup }}r^i\) con los poderes de\(R\text{?}\)

Teorema\(\PageIndex{2}\): Matrix of a Transitive Closure

Dejar\(r\) ser una relación sobre un conjunto finito y\(R\) su matriz. Dejar\(R^+\) ser la matriz\(r^+\text{,}\) del cierre transitivo de\(r\text{.}\) Entonces\(R^+ = R + R^2 + \cdots + R^n\text{,}\) usando aritmética booleana.

Usando este teorema, encontramos que\(R^+\) es la\(5\times 5\) matriz que consiste en todos por\(1's\text{,}\) lo tanto,\(r^+\) es todo de\(A \times A\text{.}\)

Algoritmos para computar cierre transitivo

Let\(r\) be a relation on the set\(\{1, 2, \dots , n\}\) with relation matrix\(R\text{.}\) La matriz del cierre transitivo se\(R^+\text{,}\) puede computar por la ecuacion\(R^+ = R + R ^2 + \cdots + R^n\text{.}\) Mediante el uso de metodos de evaluacion polinomial ordinarios, se puede computar\(R^+\) con multiplicaciones\(n -1\) matriciales:

\ begin {ecuación*} R^+ = R (I + R (I + (\ cdots R (I+ R)\ cdots)))\ end {ecuación*}

Por ejemplo, si\(n = 3\text{,}\)\(R^+ = R(I + R(I + R))\text{.}\)

Podemos hacer uso del hecho de que si\(T\) es una matriz de relaciones,\(T + T = T\) debido a que\(1 + 1 = 1\) en la aritmética booleana. Vamos\(S_k = R + R^2 + \cdots + R^k\text{.}\) Entonces

\ begin {ecuación*}\ begin {split} R &= S_1\\ S_1 (I+S_1) &=R (I+R) =R+R^2 = S_2\\ S_2 (I+S_2) &= (R+R^2) (I+R^2)\\ &= (R+R^2) + (R^2+R^3) + (R^3+R^4)\\ &=R+R^2+R^3+R^4 = S_4\ end {split}\ text {.} \ end {ecuación*}

Del mismo modo,

\ begin {ecuación*} S_4 (I+S_4) =S_8\ end {ecuación*}

y por inducción podemos probar

\ begin {ecuación*} S_ {2^k} (I+S_ {2^k}) =S_ {2^ {k+1}}\ end {ecuación*}

Observe cómo cada multiplicación matricial duplica el número de términos que se han agregado a la suma que actualmente ha calculado. En forma algorítmica, podemos calcular de la\(R^+\) siguiente manera.

Algorithm\(\PageIndex{1}\): Transitive Closure Algorithm

Dejar\(R\) ser una matriz de relación y dejar\(R^+\) ser su matriz de cierre transitivo, que se va a computar como matriz\(T\)

1.0. S=R
2.0  T=S*(I+S)
3.0 While T != S
        3.1 S = T
        3.2 T= S*(I+S) // using Boolean arithmetic
4.0 Return T

Listado\(\PageIndex{1}\)

Nota\(\PageIndex{1}\)

• A menudo, los términos de mayor potencia en\(S_{n}\) no contribuyen nada a\(R^{+}\). Cuando la condición\(T=S\) se vuelve verdadera en el Paso 3, esto es una indicación de que no se necesitan términos de mayor potencia.
• Para calcular\(R^{+}\) usando este algoritmo, no es necesario realizar más que multiplicaciones\(⌈\log_{2}⁡n⌉\) matriciales, donde\(⌈x⌉\) es el menor número entero que es mayor o igual a\(x\). Por ejemplo, si\(r\) es una relación sobre 25 elementos, no se necesitan más que multiplicaciones\(⌈\log_{2}⁡25⌉=5\) matriciales.

Un segundo algoritmo, el Algoritmo de Warshall, reduce el tiempo de cálculo al tiempo que lleva multiplicar dos matrices cuadradas con el mismo orden que la matriz de relación en cuestión.

Algorithm\(\PageIndex{2}\): Warshall's Algorithm

Dejar\(R\) ser una matriz de\(n \times n\) relación y dejar\(R^+\) ser su matriz de cierre transitivo, que se va a computar como matriz\(T\) usando aritmética booleana

1.0 T = R
2.0 for k = 1 to n:
     for i = 1 to n:
      for j = 1 to n:
        T[i,j]= T[i,j] + T[i,k] * T[k,j]
3.0 Return T

Listado\(\PageIndex{2}\)

Ejercicios

Ejercicio\(\PageIndex{1}\)

Let\(A =\{0, 1, 2, 3, 4\}\) y\(\mathcal{S}=\{(0, 1), (1, 3), (2, 3), (3, 4), (4, 1)\}\text{.}\) Compute\(\mathcal{S}^+\) usando la representación matricial de\(\mathcal{S}\text{.}\) Verifica tus resultados comprobando contra el resultado obtenido directamente de la definición de cierre transitivo.

Ejercicio\(\PageIndex{2}\)

Dejar\(A=\{1,2,3,4,6,12\}\) y\(t=\{(a,b)\mid b/a \textrm{ is a prime number}\}\text{.}\) Determinar\(t^+\) por cualquier medio. Representa tu respuesta como una matriz.

Ejercicio\(\PageIndex{3}\)

1. Dibujar dígrafos de las relaciones\(\mathcal{S}\text{,}\)\(\mathcal{S}^2\text{,}\)\(\mathcal{S}^3\), y\(\mathcal{S}^+\) dónde\(\mathcal{S}\) se define en el primer ejercicio anterior.
2. Verificar que en términos de la gráfica de\(\mathcal{S}\text{,}\)\(a \mathcal{S}^+ b\) si y solo si\(b\) es alcanzable a\(a\) lo largo de una ruta de cualquier longitud finita distinta de cero.

Contestar

1. Consulte las gráficas a continuación.
2. Por ejemplo,\(0 s^+ 4\) y usando\(S\) uno puede ir de 0 a 4 usando una ruta de longitud 3.

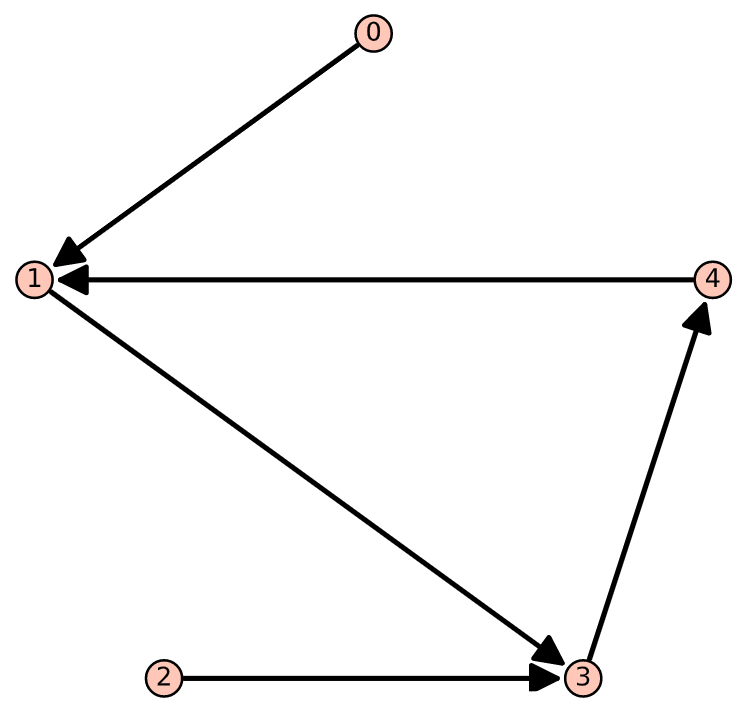
Figura\(\PageIndex{1}\): Dígrafo de\(S\)

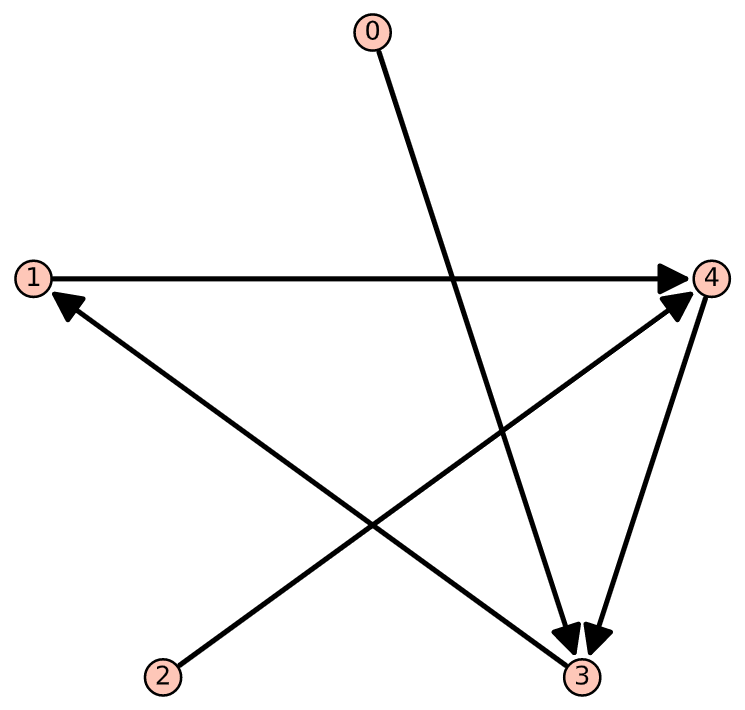
Figura\(\PageIndex{2}\): Dígrafo de\(S^{2}\)

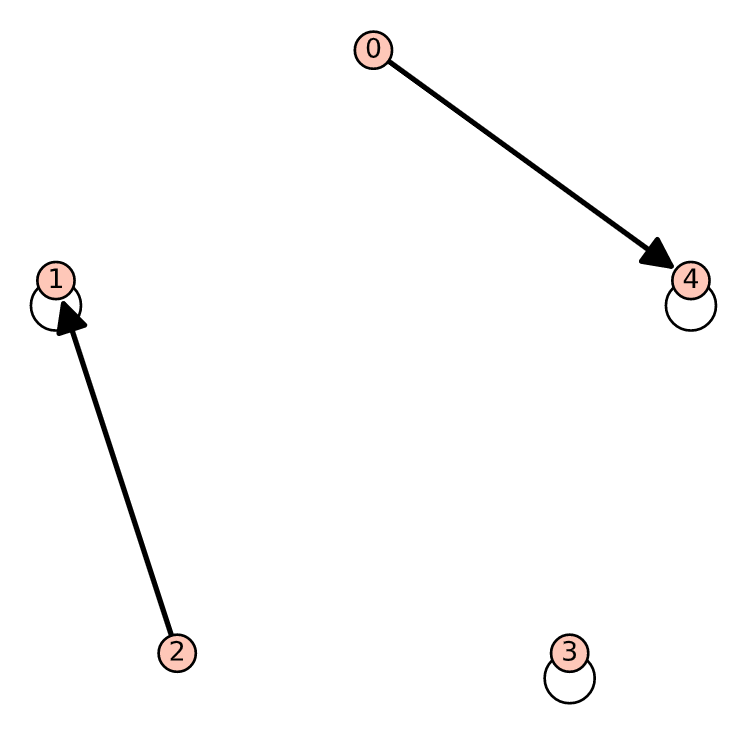
Figura\(\PageIndex{3}\): Dígrafo de\(S^{3}\)

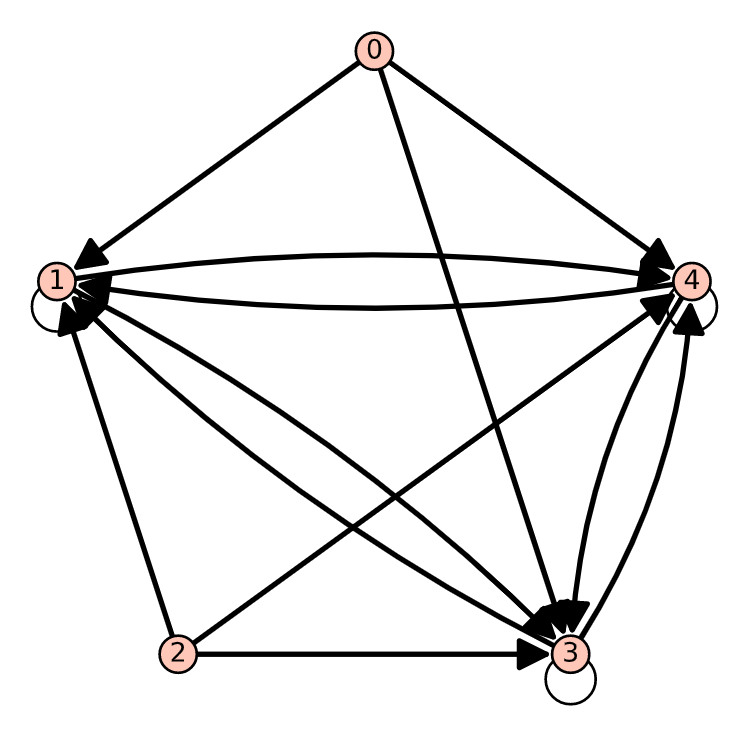
Figura\(\PageIndex{4}\): Dígrafo de\(S^{+}\)

Ejercicio\(\PageIndex{4}\)

\(r\)Sea la relación representada por el siguiente dígrafo.

1. Encuentra\(r^+\) usando la definición basada en pares de órdenes.
2. Determinar el dígrafo de\(r^+\) directamente a partir del dígrafo de\(r\text{.}\)
3. Verifica tu resultado en la parte (b) calculando el dígrafo a partir de tu resultado en la parte (a).

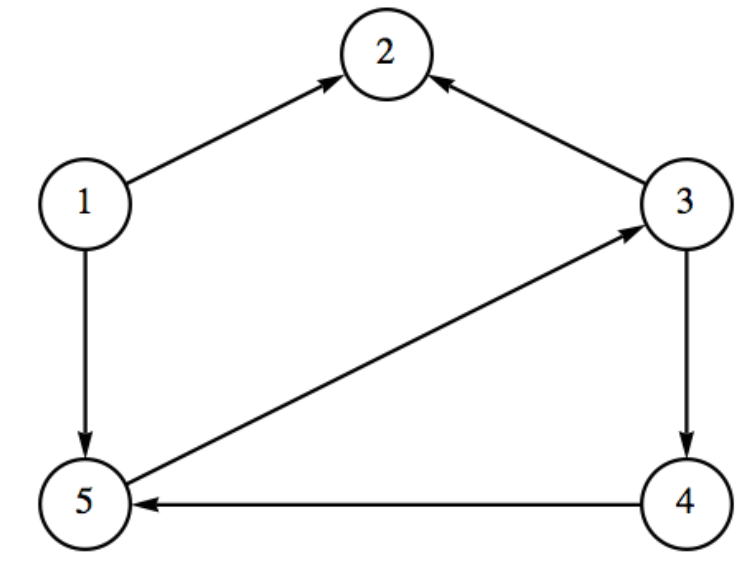
Figura\(\PageIndex{5}\): Dígrafo de\(r\) en ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

1. Definir el cierre reflexivo y el cierre simétrico imitando la definición de cierre transitivo.
2. Usa tus definiciones para calcular los cierres reflexivos y simétricos de los ejemplos en el texto.
3. ¿Cuáles son los cierres reflexivos transitivos de estos ejemplos?
4. Convénzase de que el cierre reflexivo de la relación\(<\) sobre el conjunto de enteros positivos\(\mathbb{P}\) es\(\leq\text{.}\)

Contestar

Definición: Cierre Reflejo. Dejar\(r\) ser una relación sobre\(A\text{.}\) El cierre reflexivo de\(r\) es la relación reflexiva más pequeña que contiene\(r\text{.}\)

Teorema: El cierre reflexivo de\(r\) es la unión de\(r\) con\(\{(x, x) : x\in A\}\)

Ejercicio\(\PageIndex{6}\)

¿En qué relaciones comunes\(\mathbb{Z}\) son los cierres transitivos de las siguientes relaciones?

1. \(a S b\)si y solo si\(a + 1 = b\text{.}\)
2. \(a R b\)si y solo si\(| a - b | = 2\text{.}\)

Ejercicio\(\PageIndex{7}\)

1. \(A\)Sea cualquier conjunto y\(r\) una relación sobre\(A\text{,}\) probar que\(\left(r^+\right)^+=r^+\text{.}\)
2. ¿El cierre transitivo de una relación simétrica es siempre simétrico y reflexivo? Explique.

Contestar

1. Por la definición de cierre transitivo,\(r^+\) es la relación más pequeña que contiene\(r\text{;}\) por lo tanto, es transitiva. El cierre transitivo de\(r^+\text{,}\)\(\left(r^+\right)^+\), es la relación transitiva más pequeña que contiene\(r^+\text{.}\) Since\(r^+\) es transitiva,\(\left(r^+\right)^+=r^+\text{.}\)
2. El cierre transitivo de una relación simétrica es simétrico, pero puede no ser reflexivo. Si un elemento no está relacionado con ningún elemento, entonces el cierre transitivo no relacionará ese elemento con otros.

Ejercicio\(\PageIndex{8}\)

La definición del Cierre Transitivo, Definición\(\PageIndex{1}\), de\(r\) se refiere a la “relación transitiva más pequeña que contiene\(r\) como subconjunto”. Mostrar que la intersección de todas las relaciones transitivas al\(A\) contener\(r\) es una relación transitiva que contiene\(r\) y es precisamente\(r^+\text{.}\)