13.4: Átomos de un álgebra booleana

Última actualización
Guardar como PDF

Page ID: 117189

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección veremos más de cerca algo que hemos insinuado, que es que cada álgebra booleana finita es isomórfica a un álgebra de conjuntos. Mostraremos que cada álgebra booleana finita tiene$2^n$ elementos para algunos$n$ con precisamente$n$ generadores, llamados átomos.

Considere el álgebra booleana$[B; \lor , \land, \bar{}{\hspace{3 pt}}]\text{,}$ cuyo diagrama de orden se representa en la Figura$\PageIndex{1}$

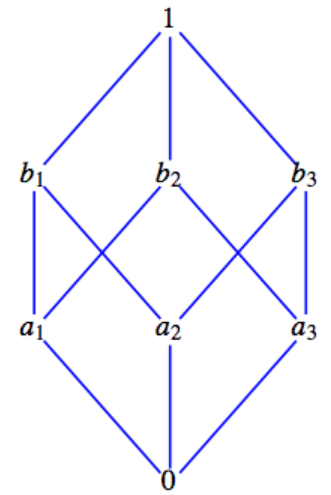$clipboard_e987d942738e8ca3623c6b968f2b06fc8.png$ Figura$\PageIndex{1}$: Ilustración del concepto de átomo

Observamos$b_3 = a_2 \lor a_3\text{;}$ que$1 = a_1 \lor a_2 \lor a_3\text{,}$$b_1 = a_1 \lor a_2\text{,}$$b_2 = a_1 \lor a_3\text{,}$ y es decir, cada uno de los elementos por encima del nivel uno puede describirse completa y singularmente en términos de los elementos en el nivel uno. Los$a_i$'s han generado de manera única los elementos no menos importantes de$B$ mucho como una base en álgebra lineal genera los elementos en un espacio vectorial. También señalamos que los$a_i$'s son los sucesores inmediatos del elemento mínimo, 0. En cualquier álgebra booleana, los sucesores inmediatos del elemento mínimo se denominan átomos. Por ejemplo, dejar$A$ ser cualquier conjunto no vacío. En el álgebra booleana$[\mathcal{P}(A); \cup , \cap, \hspace{1 mm}^c]$ (over$\subseteq$), los conjuntos singleton son los generadores, o átomos, de la estructura algebraica ya que cada elemento$\mathcal{P}(A)$ puede describirse completa y exclusivamente como la unión, o unión, de conjuntos singleton.

Definición$\PageIndex{1}$: Atom

Un elemento no mínimo$a$ en un álgebra booleana$[B; \lor , \land, \bar{}\hspace{3 pt}]$ se llama átomo si para cada$x \in B\text{,}$$x \land a = a$ o$x \land a = 0\text{.}$

La condición que nos$x \land a = a$ dice que$x$ es un sucesor de$a\text{;}$ eso es,$a \preceq x\text{,}$ como se representa en la Figura$\PageIndex{2}$ (a)

La condición$x \land a = 0$ es verdadera sólo cuando$x$ y “no$a$ están conectados”. Esto ocurre cuando$x$ es otro átomo o si$x$ es un sucesor de átomos diferente a$a\text{,}$ como se representa en la Figura$\PageIndex{2}$ (b).

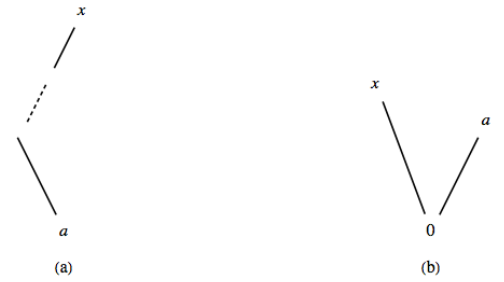$clipboard_e52d7452fa86a7f237dd1c88af0d206c1.png$ Figura$\PageIndex{2}$: Condiciones para un átomo

Una definición alternativa de un átomo se basa en el concepto de “cobertura”.

Definición$\PageIndex{2}$: The Covering Relation

Dado un álgebra booleana$[B; \lor , \land, \bar{}\hspace{3 pt}]\text{,}$$x, z \in B\text{.}$ vamos a decir que$z$ cubre$x$ iff$x \prec z$ y no existe$y \in B$ con$x \prec y \prec z\text{.}$

Se puede probar que los átomos del álgebra booleana son precisamente aquellos elementos que cubren el elemento cero.

El conjunto de átomos del álgebra booleana$\left[D_{30}; \lor , \land, \bar{\hspace{5 mm}}\right]$ es$M = \{2, 3, 5\}\text{.}$ Para ver que$a = 2$ es un átomo, dejar que$x$ sea cualquier elemento no menor de$D_{30}$ y tenga en cuenta que una de las dos condiciones$x \land 2 = 2$ o$x \land 2 = 1$ sostiene. Por supuesto, para aplicar la definición a este álgebra booleana, debemos recordarnos que en este caso el elemento 0 es 1, la operación$\land$ es el divisor más común, y la relación poset es “divide”. Entonces si$x = 10\text{,}$ tenemos$10 \land 2 = 2$ (o$2 \mid 10$), entonces la Condición 1 se mantiene. Si$x = 15\text{,}$ la primera condición no es cierta. (¿Por qué?) No obstante, la Condición 2,$15 \land 2 = 1\text{,}$ es cierta. Se anima al lector a demostrar que 3 y 5 también satisfacen la definición de un átomo. A continuación, si debemos calcular la unión (el múltiplo menos común en este caso) de todas las combinaciones posibles de los átomos 2, 3 y 5 para generar todos los elementos distintos de cero (no 1 en este caso) de$D_{30}\text{.}$ Por ejemplo,$2 \lor 3 \lor 5 = 30$ y$2 \lor 5 = 10\text{.}$ Nosotros declaramos este concepto formalmente en el siguiente teorema, que damos sin pruebas.

Teorema$\PageIndex{1}$

$\mathcal{B}=[B; \lor, \land, \hspace{1 mm}^{\bar{}}] $Sea cualquier álgebra booleana finita. $A = \left\{a_1, a_2, \dots ,a_n\right\}$Sea el conjunto de todos los átomos de$\mathcal{B}\text{.}$ Entonces cada elemento en$B$ puede expresarse de manera única como la unión de un subconjunto de$A\text{.}$

El menor elemento en relación con este teorema vale la pena señalar. Si consideramos el conjunto vacío de átomos, consideraríamos que la unión de elementos en el conjunto vacío es el elemento menor. Esto hace que la afirmación del teorema anterior sea un poco más ordenada ya que no necesitamos calificar qué elementos se pueden generar a partir de átomos.

Ahora nos preguntamos si podemos ser más definitivos sobre la estructura de diferentes álgebras booleanas de un orden dado. Ciertamente, las álgebras booleanas$\left[D_{30}; \lor , \land, \land\bar{\hspace{5 mm}} \right]$ y$[\mathcal{P}(A); \cup , \cap, \hspace{1 mm}^c]$ tienen la misma gráfica (la de la Figura$\PageIndex{1}$), el mismo número de átomos, y, en todos los aspectos, se ven iguales a excepción de los nombres de los elementos y las operaciones. De hecho, cuando aplicamos las operaciones correspondientes a los elementos correspondientes, obtenemos los resultados correspondientes. Sabemos por el Capítulo 11 que esto significa que las dos estructuras son isomórficas como álgebras booleanas. Además, las gráficas de estos ejemplos son exactamente las mismas que las de la Figura$\PageIndex{1}$, que es un álgebra booleana arbitraria de orden$8 = 2^3\text{.}$

En estos ejemplos de un álgebra booleana de orden 8, observamos que cada uno tenía 3 átomos y$2^3 = 8$ número de elementos, y todos eran isomórficos a$[\mathcal{P}(A ); \cup , \cap, \hspace{1 mm}^c]\text{,}$ donde$A = \{a, b, c\}\text{.}$ Esto nos lleva a las siguientes preguntas:

¿Hay álgebras booleanas diferentes (no isomórficas) de orden 8?
¿Cuál es la relación, si la hay, entre álgebras booleanas finitas y sus átomos?
¿Cuántos álgebras booleanas diferentes (no isomórficas) hay de orden 2? ¿Orden 3? ¿Orden 4? etc.

Las respuestas a estas preguntas se dan en el siguiente teorema y corolarios.

Teorema $\PageIndex{2}$

$\mathcal{B}=[B; \lor, \land, -]$Sea cualquier álgebra booleana finita, y deje que A sea el conjunto de todos los átomos de$\mathcal{B}\text{.}$ Entonces$[\mathcal{P}(A); \cup, \cap, {}^c]$ es isomórfico a$[B; \lor, \land, -]$

Prueba: Un isomorfismo que sirve para probar este teorema se$T:\mathcal{P}(A) \to B $ define por$T(S)= \bigvee_{a \in S}{a}\text{,}$ donde$T(\emptyset)$ se interpreta como el cero de$\mathcal{B}\text{.}$ Dejamos al lector probar que esto es efectivamente un isomorfismo.

Corolario$\PageIndex{1}$

Cada álgebra booleana finita$\mathcal{B}=[B; \lor, \land, \bar{\hspace{5 mm}}]$ tiene$2^n$ elementos para algún entero positivo$n\text{.}$

Prueba: Dejar$A$ ser el conjunto de todos los átomos de$\mathcal{B}$ y dejar$\left| A\right| = n\text{.}$ Entonces hay exactamente$2^n$ elementos (subconjuntos) en$\mathcal{P}(A)\text{,}$ y por Teorema$\PageIndex{2}$,$[B; \lor, \land, \bar{\hspace{5 mm}} ]$ es isomórfico a$[\mathcal{P}(A); \cup , \cap \hspace{1 mm}^c]$ y también debe tener$2^n$ elementos.

Corolario$\PageIndex{2}$

Todas las álgebras booleanas de orden$2^n$ son isomórficas entre sí.

Prueba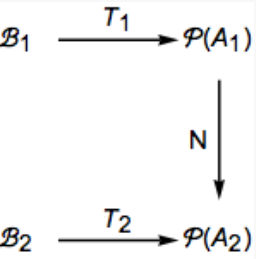: $clipboard_ed69fe7ac87c3d1a3349ef90da6e9660d.png$ Figura$\PageIndex{1}$: Isomorfismos a combinar

Cada álgebra booleana de orden$2^n$ es isomórfica a$[\mathcal{P}(A); \cup , \cap, \hspace{1 mm}^c ]$ cuándo$\lvert A \rvert= n\text{.}$ Por lo tanto, si$\mathcal{B}_1$ y$\mathcal{B}_2$ cada uno tiene$2^n$ elementos, cada uno tiene$n$ átomos. Supongamos que sus conjuntos de átomos son$A_1$ y$A_2\text{,}$ respectivamente. Sabemos que hay isomorfismos$T_1$ y$T_2\text{,}$ donde$T_i:\mathcal{B}_i \to \mathcal{P}(A_i)\text{,}$$i=1,2\text{.}$ Además tenemos un isomorfismo,$N$$\mathcal{P}(A_1)$ a partir del$\mathcal{P}(A_2)\text{,}$ cual te pedimos que pruebes en Ejercicio$\PageIndex{9}$. Podemos combinar estos isomorfismos para producir el isomorfismo$T_{2}^{-1}\circ N \circ T_1:\mathcal{B}_1 \to \mathcal{B}_2\text{,}$ que prueba el corolario.

El teorema y los corolarios anteriores nos dicen que solo podemos tener álgebras booleanas finitas de órdenes$2^1, 2^2, 2^3,. . , 2^n\text{,}$ y que todas las álgebras booleanas finitas de cualquier orden dado son isomórficas. Estas son herramientas poderosas para determinar la estructura de álgebras booleanas finitas. En la siguiente sección, discutiremos una de las formas más fáciles de describir un álgebra booleana de cualquier orden dado.

Ejercicios

Ejercicio$\PageIndex{1}$

Mostrar que$a = 2$ es un átomo del álgebra booleana$\left[D_{30}; \lor , \land, - \right]\text{.}$
Repita la parte a para los elementos 3 y 5 de$D_{30}\text{.}$
Verificar teorema$\PageIndex{1}$ para el álgebra booleana$\left[D_{30}; \lor , \land, - \right]\text{.}$

Contestar

Para$a = 3$ debemos demostrar que para cada$x \in D_{30}$ uno de lo siguiente es cierto:$x\land 3=3$ o lo$x\land 3=1\text{.}$ hacemos a través de la siguiente tabla:
\ begin {equation*}\ begin {array} {cc} x &\ textrm {verification}\\\ hline\ begin {array} {c} 1\\ 2\ 3\\ 5\\ 6\\ 10\\ 15\ 30\\ end {array} &\ begin {array} {c} 1\ land 3=1\\ 2\ tierra 3=1\\ 3\ tierra 3=3\\ 5\ tierra 3=1\\ 6\ tierra 3=3\\ 20\ tierra 3=1\\ 15\ tierra 3=3\\ 30\ tierra 3=3\\\ end {array}\\ end {array}\ end {array}\ end {ecuación*}
Para$a=5\text{,}$ un se puede realizar una verificación similar.
$6 = 2 \lor 3\text{,}$$10 = 2 \lor 5\text{,}$$15 = 3 \lor 5\text{,}$y$30 = 2 \lor 3 \lor 5\text{.}$

Ejercicio$\PageIndex{2}$

Let$A = \{a, b, c\}\text{.}$

Reescribe la definición de átomo para$[\mathcal{P}(A); \cup , \cap, c ]\text{.}$ ¿Qué$a \leq x$ significa en este ejemplo?
Encuentra todos los átomos de$[\mathcal{P}(A); \cup , \cap, c ]\text{.}$
Verificar teorema$\PageIndex{1}$ para$[\mathcal{P}(A); c, \cup , \cap ]\text{.}$

Ejercicio$\PageIndex{3}$

Verificar Teorema$\PageIndex{2}$ y sus corolarios para los álgebras booleanos en Ejercicios$\PageIndex{1}$ y$\PageIndex{2}$ de esta sección.

Contestar: Si$B = D_{30}\textrm{ }$ 30 entonces$A = \{2, 3, 5\}$ y$D_{30}$ es isomórfico a$\mathcal{P}(A)\text{,}$ donde
$\begin{array}{cc} 1\leftrightarrow \emptyset \textrm{ } & 5\leftrightarrow \{5\} \\ 2\leftrightarrow \{2\}\textrm{ } & 10\leftrightarrow \{2,5\} \\ 3\leftrightarrow \{3\}\textrm{ } & 15\leftrightarrow \{3,5\} \\ 6\leftrightarrow \{2,3\}\textrm{ } & 30\leftrightarrow \{2,3,5\} \\ \end{array}$ y$\begin{array}{c} \textrm{ Join} \leftrightarrow \textrm{ Union} \\ \textrm{ Meet}\leftrightarrow \textrm{ Intersection} \\ \textrm{ Complement}\leftrightarrow \textrm{ Set} \textrm{ Complement} \\ \end{array}$

Ejercicio$\PageIndex{4}$

Dar un ejemplo de álgebra booleana de orden 16 cuyos elementos son ciertos subconjuntos del conjunto$\{1, 2, 3, 4, 5, 6, 7\}$

Ejercicio$\PageIndex{5}$

Corolario$\PageIndex{1}$ implica que no existen álgebras booleanas de órdenes 3, 5, 6, 7, 9, etc. (órdenes diferentes a$2^n$). Sin este corolario, muestran directamente que no podemos tener un álgebra booleana de orden 3.

Insinuación

Supongamos que$[B; \lor , \land, - ]$ es un álgebra booleana de orden 3 donde$B = \{0, x, 1\}$ y mostrar que esto no puede suceder investigando las posibilidades para sus tablas de operaciones.

Contestar

Supongamos que$x \neq 0 \textrm{ or } 1$ es el tercer elemento de un álgebra booleana. Entonces solo hay un conjunto posible de tablas para unirse y reunirse, todas siguiendo de las propiedades requeridas del álgebra booleana.

\ begin {ecuación*}\ begin {array} {lr}\ begin {array} {c|c}\ lor &\ begin {array} {ccc} 0 & x & 1\\ end {array}\\\ hline\ begin {array} {c} 0\\ x\ 1\\ end {array} &\ begin {array} {ccc} 0 & x & 1\ x & x & 1\\ 1 & 1 & 1\\\ end {array}\\\ end {array} &\ begin {array} {c|c}\ land &\ begin {array} {ccc} 0 & x & 1\\\ end {array}\\\ hline\ begin {array} {c} 0\\ x\\ 1\\ end {array} &\ begin {array} {ccc} 0 & 0 & 0\\ 0 & x & x\\ 0 & x\\ 0 & x & 1\\ end {array}\\ end {array}\ end {array}\ end array}\ end {ecuación*}

A continuación, para encontrar el complemento de$x$ queremos$y$ tal que$x \land y = 0$ y$x \lor y = 1\text{.}$ Ningún elemento satisfaga ambas condiciones; de ahí que la celosía no se complemente y no puede ser un álgebra booleana. La falta de un complemento también se puede ver a partir del diagrama de ordenamiento del cual$\land$ y$\lor$ debe derivarse.

Ejercicio$\PageIndex{6}$

Hay muchos álgebras booleanas diferentes, pero isomórficas, con dos elementos. Describa uno de esos álgebra booleana que se deriva de un conjunto de$\mathcal{P}(A)\text{,}$ potencias, bajo$\subseteq\text{.}$ Describir un segundo que se describe$D_n\text{,}$ para algunos$n \in P\text{,}$ bajo “divide”.
Dado que los elementos de un álgebra booleana de dos elementos deben ser los elementos mayores y menores, 1 y 0, las tablas para las operaciones$\{0, 1\}$ están determinadas por las leyes del álgebra booleana. Escriba las tablas de operaciones para$[\{0, 1\}; \lor , \land, -]\text{.}$

Ejercicio$\PageIndex{7}$

Encuentra un álgebra booleana con un número infinitamente contable de elementos.

Contestar

$X$Sea cualquier conjunto infinitamente contable, como los enteros. Un subconjunto de$X$ es cofinito si es finito o su complemento es finito. El conjunto de todos los subconjuntos cofinitos de$X$ es:

Contablemente infinito - esto podría no ser obvio, pero aquí hay una pista. Asumir$X=\left\{x_0,x_1,x_2,\ldots \right\}\text{.}$ Por cada subconjunto finito$A$ de$X\text{,}$ mapa que se establece en el entero$\sum _{i=0}^{\infty } \chi _A \left(x_i\right)2^i$ Puedes hacer algo similar a conjuntos que tienen un complemento finito, pero mapearlos a enteros negativos. Solo se necesita hacer un ajuste menor para acomodar tanto el conjunto vacío como$X\text{.}$
Cerrado bajo unión
Cerrado bajo intersección, y
Cerrada bajo complementación.

Por lo tanto, si$B =\{A \subseteq X : A \textrm{ is cofinite}\}\text{,}$ entonces$B$ es un álgebra booleana contable bajo las operaciones establecidas habituales.

Ejercicio$\PageIndex{8}$

Demostrar que el producto directo de dos álgebras booleanas es un álgebra booleana.

Insinuación: “Copiar” el comprobante correspondiente para grupos en la Sección 11.6.

Ejercicio$\PageIndex{9}$

Demostrar si dos conjuntos finitos$A_1$ y$A_2$ ambos tienen$n$ elementos entonces$[\mathcal{P}(A_1); \cup , \cap, \hspace{1 mm}^c]$ es isomórfico a$[\mathcal{P}(A_2); \cup , \cap, \hspace{1 mm}^c]$

Ejercicio$\PageIndex{10}$

Demostrar que un elemento de un álgebra booleana es un átomo si y solo si cubre el elemento cero.