15.5: Actividades
- Page ID
- 118250
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
En cada una de las siguientes, idear una gráfica que contenga el tipo de caminata solicitado. (No es necesario crear una gráfica que contenga los tres tipos de caminatas; puede dibujar tres gráficas separadas).
- Un camino cerrado que no es un sendero.
- Un sendero abierto que no es un camino.
- Un sendero cerrado que no es un camino.
Diseñar una gráfica con exactamente cuatro vértices, cada uno de los cuales tiene grado\(5\text{,}\) para que la gráfica sea
- no conectados.
- conectado.
En cada una de las siguientes, idear una gráfica conectada con al menos cinco vértices que tenga las propiedades solicitadas. Hazlo sin mirar las gráficas de ejemplo en este capítulo. (No es necesario crear una gráfica que contenga todas las propiedades; puede dibujar una gráfica separada para cada tarea a continuación).
- Contiene un puente.
- Cada borde es un puente.
- Contiene un vértice de articulación.
- Cada vértice de grado al menos\(2\) es un vértice de articulación.
¿Aumentar el número de bordes en una gráfica aumenta su conectividad de borde?
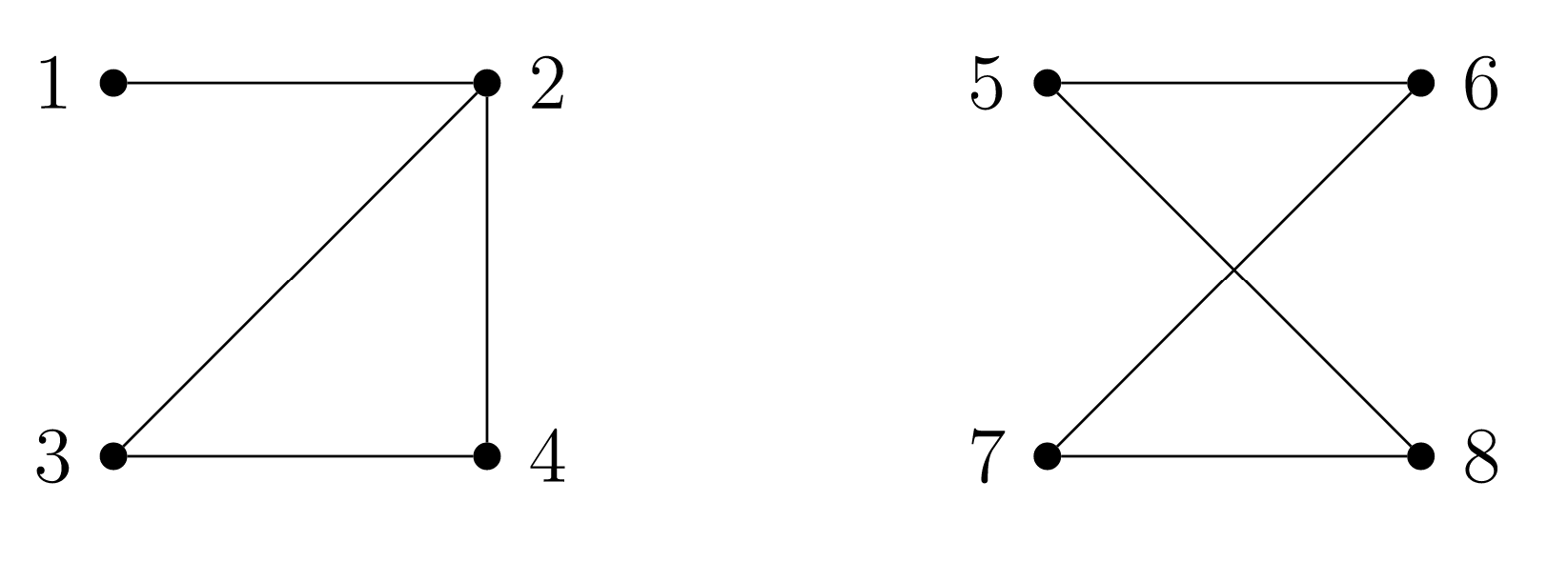
En la gráfica de Figura\(\PageIndex{1}\), explique por qué el subgrafo formado por vértices\(2\text{,}\)\(3\text{,}\) y\(4\text{,}\) junto con todos los bordes incidentes a estos vértices, falla la definición formal de componente conectado. Identificar cuál de las dos condiciones de esta definición formal falla el subgrafo, y describir explícitamente cómo el subgrafo no cumple esa condición.
Supongamos que\(G\) es una gráfica simple, no conectada con\(n\) vértices que es máxima con respecto a estas propiedades. Es decir, si intentaste hacer una gráfica más grande en la que\(G\) sea una subgráfica, esta gráfica más grande perderá al menos una de las propiedades (a) simple, (b) no conectada, o (c) tiene\(n\) vértices.
¿Qué implica ser máximo con respecto a estas propiedades sobre Es\(G\text{?}\) decir, qué propiedades adicionales deben\(G\) poseer debido a esta suposición?
Un circuito de Euler es un sendero cerrado en una gráfica conectada G que atraviesa cada borde de G. Ya que debe ser un sendero, se podría decir que un circuito de Euler atraviesa cada borde de G exactamente una vez (además de terminar en el mismo nodo en el que comienza).
Demostrar que si una gráfica conectada contiene un circuito de Euler, entonces cada vértice en esa gráfica debe tener un grado par.


