9.1: Respuestas
- Page ID
- 112945
Sección 2.1
- Sólo las letras a), c) y e) son declaraciones.
-
- false
- false
- false
- true
-
- \(\pi\notin\mathbb{Z}\)
- \(1^3+2^3+3^3 \neq 3^2\cdot4^2/4\)
- \(u\)no es una vocal
- Esta afirmación es verdadera o falsa.
-
- true
- true
- true
- false
- false
- true
- Por definición, un número racional puede escribirse como una relación de dos enteros. Después de multiplicar el numerador por 7, todavía tenemos una relación de dos enteros. Por el contrario, dado cualquier número racional\(x\), podemos multiplicar el denominador por 7, obtenemos otro número racional\(y\) tal que\(7y=x\). De ahí que los dos conjuntos\(7\mathbb{Q}\) y\(\mathbb{Q}\) contengan la misma colección de números racionales. En contraste,\(0\mathbb{Q}\) contiene sólo un número, a saber, 0. Por lo tanto,\(0\mathbb{Q}\neq\mathbb{Q}\).
Sección 2.2
-
- \(p\wedge q\)
- \(\overline{q}\wedge r\)
- \(\overline{p}\vee \overline{q}\)
- \((p\vee q) \wedge \overline{p\wedge q}\)
-
- \(p\wedge q\); siempre falso independientemente del valor de\(r\).
- \(p\vee q\); siempre cierto independientemente del valor de\(r\).
- \((p\wedge q)\vee r\); verdadero si\(r\) es verdadero, y falso si\(r\) es falso.
- \(\overline{q}\wedge r\); verdadero si\(r\) es verdadero, y falso si\(r\) es falso.
-
- false
- true
-
- \((4\leq x)\wedge (x\leq 7)\)
- \((4 < x)\wedge (x\leq 7)\)
- \((4\leq x)\wedge (x < 7)\)
Sección 2.3
-
- \(p\Rightarrow q\)
- \(r\Rightarrow p\)
- \(\overline{p}\Rightarrow q\)
- \(\overline{p}\Rightarrow r\)
- \((\overline{p}\wedge q)\Rightarrow r\)
-
- \(p\Rightarrow q\), que es falso.
- \(p\Rightarrow r\), que es verdadero si\(r\) es verdadero, y es falso si\(r\) es falso.
- \((p\vee q)\Rightarrow r\), que es verdadero si\(r\) es verdadero, y es falso si\(r\) es falso.
-
- \(x^3-3x^2+x-3=0 \Rightarrow x=3\)
- \(x^3-3x^2+x-3=0 \Rightarrow x=3\)
- \(x=3 \Rightarrow x^3-3x^2+x-3=0\)
- \ (\ begin {array} {|c|c|c|c|c|}\ hline p & q & r & p\ cuña q & (p\ cuña q)\ vee r\\\ hline T & T & T & T &\ qquad\; T\ T & T &F & T &\ qquad\; T\ T & T &\ T &F & F &\ qquad\; F\\ F & T T & F &\ qquad\; T\\ F & T &F &\ qquad\; F\\ F &F & T & F &\ qquad\; T\\ F &F & F &\ qquad\; F\\ hline\ end {array}\ hspace {0.5 in}
\ begin {array} {|c|c|c|c|c|c| c|}\ hline p & q & r & p\ vee q & p\ cuña r & (p\ vee q)\ Rightarrow (p\ cuña r)\\\ hline T & T & T & T & T & T & F & T & F & F & F & F & T & T & T & T & T\\ T & F & T & F & F & F & F & F & T & F & T & F & F & T & F & F & T & F & F & F & T & F & F & T & F & F & F & F & T\\\ hline\ final {matriz}\) -
- Usando una tabla de la verdad, encontramos que la implicación\((p\wedge q) \Rightarrow(q\vee r)\) es siempre cierta. De ahí que ningún valor de verdad de\(p\) haría\((p\wedge q)\Rightarrow(q\vee r)\) falso.
- De una tabla de verdad, encontramos que,\((q\wedge r)\Rightarrow (p\wedge q)\) es falsa sólo cuando\(p\) es falsa. Podemos sacar la misma conclusión sin usar ninguna tabla de la verdad. Una implicación es falsa sólo cuando su hipótesis (en este caso,\(q\wedge r\)) es verdadera y su conclusión (en este caso,\(p\wedge q\)) es falsa. \(q\wedge r\)Para ser verdad, necesitamos ambas\(q\) y\(r\) para ser verdad. Ahora\(q\) es cierto y\(p\wedge q\) es falso requieren\(p\) ser falsos.
Sección 2.4
-
- \(p\Leftrightarrow q\)
- \(r\Leftrightarrow\overline{p}\)
- \(r\Leftrightarrow(q\wedge\overline{p})\)
- \(r\Leftrightarrow(p\wedge q)\)
-
- \(p\Leftrightarrow q\), que es falso.
- \(p\Leftrightarrow r\), que es verdadero si\(r\) es verdadero, y es falso si\(r\) es falso.
- \((p\vee q)\Leftrightarrow r\), que es verdadero si\(r\) es verdadero, y es falso si\(r\) es falso.
-
- true
- false
- false
- false
- Decimos que\(n\) es impar si y sólo si\(n=2q+1\) para algún entero\(q\).
Sección 2.5
- \(\begin{array}{|c|c|c|c|c|c|c|} \hline p & q & p\vee q & \overline{p\vee q} & \overline{p} & \overline{q} & \overline{p}\wedge\overline{q} \\ \hline T & T & T & F & F & F & F \\ T & F & T & F & F & T & F \\ T & T & T & F & T & F & F \\ T & F &F & T & T & T & T \\ \hline \end{array}\)
- Sólo (b) es una tautología, como se indica en las tablas de verdad a continuación.
- \(\begin{array}{|c|c|c|c|c|} \hline p & q & \overline{p} & \overline{p}\vee q & (\overline{p}\vee q)\Rightarrow p \\ \hline T & T & F & T & \qquad\;T \\ T & F & F & F & \qquad\;T \\ F & T & T & T & \qquad\; F \\ F & F & T & T & \qquad\; F \\ \hline \end{array}\)
- \(\begin{array}{|c|c|c|c|c|c|} \hline p & q & p\Rightarrow q & \overline{q} & p\Rightarrow\overline{q} & (p\Rightarrow q)\vee(p\Rightarrow\overline{q}) \\ \hline T &T &T & F & F &T \\ T &F &F & T & T &T \\ F &T &T & F & T &T \\ F &F &F & T & T &T \\ \hline \end{array}\)
- \(\begin{array}{|c|c|c|c|c|} \hline p & q & r & p\Rightarrow q & (p\Rightarrow q)\Rightarrow r \\ \hline T &T &T & T & \qquad\quad T \\ T &T &F & T & \qquad\quad F \\ T &F &T & F & \qquad\quad T \\ T &F &F & F & \qquad\quad T \\ F &T &T & T & \qquad\quad T \\ F &T &F & T & \qquad\quad F \\ F &F &T &T & \qquad\quad T \\ F &F &F &T & \qquad\quad F \\ \hline \end{array}\)
- Las pruebas se muestran a continuación sin explicaciones. Asegúrate de rellenarlos.
- \(\begin{array}{lclc} (p\wedge q)\Rightarrow r &\equiv& \overline{p\wedge q}\vee r & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& (\overline{p}\vee\overline{q})\vee r & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& \overline{p}\vee(\overline{q}\vee r) & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& p\Rightarrow(\overline{q}\vee r) & ( \; \; \; \; \; \; \; \; \; \; \; \;) \end{array}\)
- \( \begin{array}{lclc} (p\Rightarrow\overline{q}) \wedge (p\Rightarrow\overline{r}) &\equiv& (\overline{p}\vee\overline{q}) \wedge (\overline{p}\vee\overline{r}) & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& \overline{p}\vee(\overline{q}\wedge\overline{r}) & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& \overline{p}\vee\overline{q\vee r} & ( \; \; \; \; \; \; \; \; \; \; \; \;) \\ &\equiv& \overline{p\wedge(q\vee r)} & ( \; \; \; \; \; \; \; \; \; \; \; \;) \end{array}\)
-
-
Converse: Si\(ABC\) el triángulo es un triángulo rectángulo, entonces\(ABC\) es isósceles y contiene un ángulo de 45 grados. Inversa: Si\(ABC\) el triángulo no es isósceles o no contiene un ángulo de 45 grados, entonces no\(ABC\) es un triángulo rectángulo. Contrapositivo: Si\(ABC\) el triángulo no es un triángulo rectángulo, entonces no\(ABC\) es isósceles o no contiene un ángulo de 45 grados. -
Converse: Si el cuadrilátero\(ABCD\) es tanto un rectángulo como un rombo, entonces\(ABCD\) es un cuadrado. Inversa: Si el cuadrilátero no\(ABCD\) es un cuadrado, entonces no es un rectángulo o no un rombo. Contrapositivo: Si el cuadrilátero no\(ABCD\) es un rectángulo o no un rombo, entonces no\(ABCD\) es un cuadrado.
-
-
- true
- true
- false
- Únicamente b).
-
- \(p\wedge q\)
- \(p\wedge\overline{q}\)
- \(p\wedge q\)
Sección 2.6
-
- Existe un entero\(n\) tal que\(n\) es primo y\(n\) es par.
- Para todos los enteros\(n\), si\(n>2\), entonces\(n\) es primo o\(n\) es par.
- Existe un entero\(n\) tal que\(n\) es primo, y o bien\(n\) es par o\(n>2\).
- Para todos los enteros\(n\), si\(n\) es primo y\(n\) es par, entonces\(n\leq2\).
-
- true
- true
- false
- false
- true
-
- \(\exists x<0\,\exists y,z\in\mathbb{R}\,(y<z \wedge xy\leq xz)\)
- \(\exists x\in\mathbb{Z}\,[\overline{p(x)}\wedge\overline{q(x)}]\)
- \(\exists x,y\in\mathbb{R}\,[p(x,y)\wedge\overline{q(x,y)}]\)
-
-
\(\forall x,y\in\mathbb{R}\,(x+y=y+x)\) \(\exists x,y\in\mathbb{R}\,(x+y\neq y+x)\) Existen números reales\(x\) y\(y\) tal que\(x+y\neq y+x\). -
\(\forall x\in\mathbb{R}^+\,\exists y\in\mathbb{R}\,(y^2=x)\) \(\exists x\in\mathbb{R}^+\,\forall y\in\mathbb{R}\,(y^2\neq x)\) Existe un número real positivo\(x\) tal que para todos los números reales\(y\),\(y^2\neq x\). -
\(\exists y\in\mathbb{R}\,\forall x\in\mathbb{Z}\,(2x^2+1>x^2y)\) \(\forall y\in\mathbb{R}\,\exists x\in\mathbb{Z}\,(2x^2+1\leq x^2y)\) Por cada número real\(y\), existe un entero\(x\) tal que\(2x^2+1\leq x^2y\).
-
- El enunciado “un cuadrado debe ser un paralelogramo” significa, simbólicamente,\[\forall PQRS\,(PQRS \mbox{ is a square} \Rightarrow PQRS \mbox{ is a parallelogram}), \nonumber\] pero la declaración “un cuadrado no debe ser un paralelogramo” significa\[\forall PQRS\,(PQRS \mbox{ is a square} \Rightarrow PQRS \mbox{ is not a parallelogram}). \nonumber\] La segunda declaración no es la negación de la primera. La negación correcta, en símbolo, es\[\exists PQRS\,(PQRS \mbox{ is a square} \wedge PQRS \mbox{ is a parallelogram}). \nonumber\] En palabras, significa “existe un cuadrado que no es un paralelogramo”.
Sección 3.1
- Colocar seis dominó horizontalmente en cada fila cubre todo el tablero de ajedrez.
- Vamos\(f(x)=x^3-12x+2\). De la siguiente tabla\[\begin{array}{|c||*{9}{r|}} \hline x & -4 & -3 & -2 & -1 & 0 & 1 & 2 & 3 & 4 \\ \hline f(x) & -14 & 12 & 18 & 13 & 2 & -9 & -14 & -7 & 18 \\ \hline \end{array} \nonumber\] concluimos\(x^3-12x+2=0\) que hay una solución entre\(-4\) y\(-3\), otra entre 0 y 1, y una tercera entre 3 y 4. Por lo que tiene al menos tres soluciones reales.
OBSERVACIÓN. El Teorema Fundamental del Álgebra afirma que un polinomio real de grado\(n\) tiene como máximo raíces\(n\) reales. De ahí que la ecuación dada tenga exactamente tres soluciones reales.
- \(n=3\).
Sección 3.2
- No,\(2^3+1=9\) es compuesto.
- Según (i), el número\(\sqrt{2}\) es irracional. Se deduce de (ii) que también\(\sqrt[4]{2} = \sqrt{\sqrt{2}}\) es irracional. Aplicando (ii) una vez más, concluimos que\(\sqrt[8]{2} = \sqrt{\sqrt[4]{2}}\) es irracional.
-
- El enunciado es falso, porque\((-3)^2 > (-2)^2\), pero\(-3\not>-2\).
- El enunciado es falso, porque cuando\(n=41\),\[n^2+n+41 = 41^2+41+41 = 41(41+1+1) = 41\cdot 43 \nonumber\] es compuesto.
Sección 3.3
-
- Demostraremos el contrapositivo de la declaración dada. Es decir, vamos a probar que si\(n\) es impar, entonces\(n^2\) es impar. Si\(n\) es impar, podemos escribir\(n=2q+1\) para algún entero\(q\). Entonces\[n^2 = (2q+1)^2 = 4q^2+4q+1 = 2(2q^2+2q)+1, \nonumber\] donde\(2q^2+2q\) es un entero. Esto demuestra que\(n^2\) es extraño.
- Supongamos que la declaración dada es falsa. Es decir, supongamos que\(n^2\) es par, pero\(n\) es extraño. Dado que\(n\) es impar,\(n=2q+1\) para algún entero\(q\). Entonces\[n^2 = (2q+1)^2 = 4q^2+4q+1 = 2(2q^2+2q)+1, \nonumber\] donde\(2q^2+2q\) es un entero. Esto demuestra que\(n^2\) es extraño, lo que contradice la suposición de que\(n^2\) es par. Por lo tanto, la afirmación dada debe ser cierta.
- Supongamos que existen algunos números\(a\neq b\) tales que\(a^2+b^2=2ab\). Entonces eso\[0 = a^2-2ab+b^2 = (a-b)^2 \nonumber\] habría dado a entender\(a=b\). Esto contradice la suposición de que\(a\neq b\). Por lo tanto,\(a^2+b^2\neq 2ab\).
- Supongamos que\((p\Rightarrow q) \vee (p\Rightarrow \overline{q})\) es falso para algunas declaraciones lógicas\(p\) y\(q\). Para que una disyunción sea falsa, necesitamos
- \(p\Rightarrow q\)ser falso, y
- \(p\Rightarrow \overline{q}\)ser falso.
Ellos a su vez requieren
- \(p\)ser verdad y\(q\) ser falso, y
- \(p\)ser verdad y\(\overline{q}\) ser falso.
Tener\(\overline{q}\) falso implicaría\(q\) es cierto, lo que contradice lo que encontramos. Por lo tanto, la fórmula lógica dada es siempre cierta, de ahí, una tautología.
Sección 3.4
- Se procede por inducción en\(n\). Cuando\(n=1\), el lado izquierdo de la identidad se reduce a\(1^3=1\), y el lado derecho se vuelve\(\frac{1^2\cdot2^2}{4}=1\). De ahí que la identidad se mantenga cuando\(n=1\). Supongamos que la identidad se mantiene cuando\(n=k\) para algún entero\(k\geq1\); es decir, asumir\[1^3+2^3+3^3+\cdots+k^3 = \frac{k^2(k+1)^2}{4} \nonumber\] para algún entero\(k\geq1\). Queremos mostrar que también sostiene cuándo\(n=k+1\); es decir, queremos mostrar que\[1^3+2^3+3^3+\cdots+(k+1)^3 = \frac{(k+1)^2(k+2)^2}{4}. \nonumber\] Usando la hipótesis inductiva, encontramos\[\begin{array}{rcl} 1^3+2^3+3^3+\cdots+(k+1)^3 &=& 1^3+2^3+3^3+\cdots+k^3+(k+1)^3 \\ &=& \frac{k^2(k+1)^2}{4} + (k+1)^3 \\ &=& \frac{(k+1)^2[k^2+4(k+1)]}{4} \\ &=& \frac{(k+1)^2(k^2+4k+4)}{4} \\ &=& \frac{(k+1)^2(k+2)^2}{4}. \end{array} \nonumber\] Por lo tanto, la identidad también sostiene cuándo\(n=k+1\). Esto completa la inducción.
Sección 3.5
- 1. Se procede por inducción en\(n\). Cuando\(n=1\), el producto\(n(n+1)(n+2)\) se convierte\(1\cdot2\cdot3=6\), que obviamente es un múltiplo de 3. De ahí que el reclamo se mantenga cuando\(n=1\). Supongamos que la afirmación se mantiene cuando\(n=k\) para algún entero\(k\geq1\); es decir, supongamos que\(k(k+1)(k+2)\) es un múltiplo de 3 para algún entero\(k\geq1\). Entonces podemos escribir\[k(k+1)(k+2) = 3q \nonumber\] para algún entero\(q\). Queremos demostrar que el reclamo sigue siendo válido cuando\(n=k+1\). Es decir, queremos mostrar que también\((k+1)(k+2)(k+3)\) es un múltiplo de 3. Entonces queremos encontrar un entero\(Q\) tal que\[(k+1)(k+2)(k+3) = 3Q. \nonumber\] Observemos que, usando la hipótesis inductiva,\[\begin{array}{rcl} (k+1)(k+2)(k+3) &=& k(k+1)(k+2) + 3(k+1)(k+2) \\ &=& 3q + 3(k+1)(k+2) \\ &=& 3\,[q+(k+1)(k+2)], \end{array} \nonumber\] donde\(q+(k+1)(k+2)\) es un entero. De ahí,\((k+1)(k+2)(k+3)\) es un múltiplo de 3. Esto completa la inducción.
-
- \(S_n=1-\frac{1}{(n+1)!}\)para todos los enteros\(n\geq1\).
-
- \(T_n = \frac{n+1}{2n+3}\)para todos los enteros\(n\geq0\).
Sección 3.6
- Se procede por inducción en\(n\). Cuando\(n=1\), el lado izquierdo de la identidad se reduce a\(F_1^2=1^2=1\), y el lado derecho se vuelve\(F_1F_2=1\cdot1=1\). De ahí que la identidad se mantenga cuando\(n=1\). Supongamos que la identidad se mantiene cuando\(n=k\) para algún entero\(k\geq1\); es decir, asumir\[F_1^2+F_2^2+F_3^2+\cdots+F_k^2 = F_k F_{k+1} \nonumber\] para algún entero\(k\geq1\). Queremos mostrar que también sostiene cuándo\(n=k+1\); es decir, queremos mostrar que\[F_1^2+F_2^2+F_3^2+\cdots+F_{k+1}^2 = F_{k+1} F_{k+2}. \nonumber\] Usando la hipótesis inductiva, encontramos\[\begin{array}{rcl} F_1^2+F_2^2+F_3^2+\cdots+F_{k+1}^2 &=& F_1^2+F_2^2+F_3^2+\cdots+F_k^2+F_{k+1}^2 \\ &=& F_k F_{k+1} + F_{k+1}^2 \\ &=& F_{k+1} (F_k+F_{k+1}) \\ &=& F_{k+1} F_{k+2}. \end{array} \nonumber\] Por lo tanto, la identidad también sostiene cuándo\(n=k+1\). Esto completa la inducción.
Sección 4.1
-
- \(\{-5,-4,-3,-2,-1,0,1,2,3\}\)
- \(\{1,2,3\}\)
- \(\{0,-2,3\}\)
- \(\{-3,3\}\)
-
- \(\{n\in\mathbb{Z} \mid n<0\}\)
- \(\{n\in\mathbb{Z} \mid n \text{ is a perfect cube}\}\)
- \(\{n\in\mathbb{Z} \mid n \text{ is a perfect square}\}\)
-
- \(\mathbb{Z}^-\)
- \(5\mathbb{Z}\)
- \(4+6\mathbb{Z}\)
observación. No podemos escribir (b) como\(\mathbb{Z}^3\) y (c) como\(\mathbb{Z}^2\), porque\(\mathbb{Z}^3\) y\(\mathbb{Z}^2\) significar otra cosa. Si bajamos 0 de (e), entonces\(\{4,8,12,\ldots\}=4\mathbb{N}\). Sin embargo, la inclusión de 0 hace que sea más difícil describir (d) en forma de\(4S\).
-
- \((-4,7)\)
- \((-4,7]\)
- \((0,7]\)
-
- 10
- 11
- 7
-
- true
- true
- true
- false
-
- Es incorrecto escribir\((3,7]=3<x\leq7\) porque\((3,7]\) es un conjunto, pero\(3<x\leq7\) es una sentencia lógica.
- No, porque ambos\(\{x\in\mathbb{R}\mid x^2<0\}\) y\(\emptyset\) son conjuntos, por lo que debemos usar un signo igual para compararlos. La notación\(\equiv\) sólo se aplica a las sentencias lógicas. La forma correcta de decirlo es “\(\{x\in\mathbb{R}\mid x^2<0\} = \emptyset\).”
Sección 4.2
-
- true
- true
- true
- true
- true
- false
- Tenemos\(\mathbb{Z}\subseteq\mathbb{N}\) porque cada entero\(n\) es también un número racional, ya que podemos escribirlo como el número racional\(\frac{n}{1}\).
- Sí, esta es la propiedad transitiva.
-
- \(\big\{\emptyset,\{a\},\{\{b\}\},\{a,\{b\}\}\big\}\)
-
- False, porque el conjunto\(\{a\}\) no se puede encontrar en\(\{a,b,c\}\) como un elemento.
- Falso, porque\(a\), el único elemento en\(\{a\}\), no se puede encontrar en\(\{\{a\},b,c\}\) como un elemento.
- Falso. Para\(\{a\}\in\wp(\{\{a\},b,c\})\), el conjunto\(\{a\}\) debe ser un subconjunto de\(\{\{a\},b,c\}\}\). Este medio\(a\) debe pertenecer a\(\{\{a\},b,c\}\), lo cual no es cierto.
Sección 4.3
-
- \(\{-4,-3,-2,-1,0,1,2,3,4\}\)
- \(\{-3,-2,-1,0,1,2,3,4\}\)
- \(\{-3,-2,-1,0,1,2,3,\ldots\}\)
-
- false
- false
-
- \(E\cap D\)
- \(\overline{E}\cup B\)
- Por ejemplo, tomar\(A=\{x\}\), y\(B=\{\{x\},x\}\).
- Asumir\(A\subseteq C\) y\(B\subseteq C\), queremos demostrarlo\(A\cup B \subseteq C\). En este sentido\(x\in A\cup B\), vamos, queremos demostrarlo\(x\in C\) también. Ya que\(x\in A\cup B\), la definición de conjunto de unión asevera que cualquiera\(x\in A\) o\(x\in B\).
En ambos casos, encontramos\(x\in C\). Esto lo demuestra\(A\cup B\subseteq C\).
- Caso 1: Si\(x\in A\), entonces\(A\subseteq C\) implica eso\(x\in C\).
- Caso 2: Si\(x\in B\), entonces\(B\subseteq C\) implica eso\(x\in C\).
-
- La notación\(\cap\) se utiliza para conectar dos conjuntos, pero “\(x\in A\)” y “\(x\in B\)” son ambas sentencias lógicas. También deberíamos usar\(\Leftrightarrow\) en lugar de\(\equiv\). El comunicado debió haber sido escrito como “\(x\in A \,\wedge\, x\in B \Leftrightarrow x\in A\cap B\).”
- Si lo leemos en voz alta, suena perfecto:\[\mbox{If $x$ belongs to $A$ and $B$, then $x$ belongs to $A\cap B$}. \nonumber\] El problema es que cada notación tiene su propio significado y uso específico. En este caso, no\(\wedge\) es exactamente un reemplazo para la palabra inglesa “y”. En cambio, es la notación para unir dos sentencias lógicas para formar una conjunción. Antes\(\wedge\), tenemos “\(x\in A\),” que es una afirmación lógica. Pero, después\(\wedge\), tenemos “\(B\),” que es un conjunto, y no una afirmación lógica. Debe escribirse como “\(x\in A\,\wedge\,x\in B \Rightarrow x\in A\cap B\).”
Sección 4.4
-
- \(\{(-2,0), (-2,4), (2,0), (2,4)\}\)
- \(\{(-2,-3), (-2,0), (-2,3), (-2,-3), (-2,0), (-2,3)\}\)
- \(2\cdot2\cdot2\cdot3 = 24\).
-
- \(\{(-2,\emptyset),(-2,\{-2\}),(-2,\{2\}),(-2,\{-2,2\}), ( 2,\emptyset),( 2,\{-2\}),( 2,\{2\}),( 2,\{-2,2\})\}\)
Sección 4.5
- \(\bigcap_{n=1}^\infty A_n = [0,2)\),\(\bigcup_{n=1}^\infty A_n = (-1,\infty)\).
- \(\bigcap_{n=0}^\infty C_n = \emptyset\),\(\bigcup_{n=0}^\infty C_n = \mathbb{N}\cup\{0\}\).
- \(\bigcap_{n\in\mathbb{N}} E_n = E_0 = \{0\}\),\(\bigcup_{n\in\mathbb{N}} E_n = \mathbb{Z}\).
- \(\bigcup_{i\in I} A_i = [1,\infty)\),\(\bigcap_{i\in I} A_i = \{1\}\).
- \(\bigcap_{x\in(1,2)} (1-2x,x^2) = [-1,1]\),\(\bigcup_{x\in(1,2)} (1-2x,x^2) = (-3.4)\).
- \(\bigcap_{r\in(0,\infty)} A_r = \{(0,0)\}\),\(\bigcup_{r\in(0,\infty)} A_r = \mathbb{R}^*\times\mathbb{R}^+ \cup \{(0,0)\}\).
Sección 5.1
-
- 3
- 3
- 3
- 1
- Afirmamos que el subconjunto\((3,5)\) no tiene un elemento más pequeño. Para ver por qué, supongamos que tiene un elemento más pequeño\(x\). El punto medio entre 3 y\(x\) es el número\(\frac{3+x}{2}\), y\[3 < \frac{3+x}{2} < x < 5. \nonumber\] Esto significa que también\(\frac{3+x}{2}\) está dentro del intervalo\((3,5)\), y es menor que\(x\). Esto contradice la minimalidad de\(x\). Así, el intervalo\((3,5)\) no tiene un elemento más pequeño. En consecuencia, el intervalo no\((3,5]\) está bien ordenado.
- Sabemos que\(\mathbb{N}\) está bien ordenado. Dado que\(2\mathbb{N}\) es un subconjunto de\(\mathbb{N}\), y\(2\mathbb{N}\) es claramente no vacío, concluimos del Problema 4 que también\(2\mathbb{N}\) está bien ordenado.
Sección 5.2
-
- 23, 1
- \(-11\), 1
- \(-6\), 13
- Esto es una consecuencia inmediata del Corolario 5.2.2.
-
- Dejar\(n\) ser cualquier entero. Entonces\(n\bmod3=0,1,2\).
En los tres casos, hemos demostrado que\(n^3-n\) es un múltiplo de 3.
- Observamos que\[n^3-n = n(n^2-1) = n(n-1)(n+1) = (n-1)n(n+1) \nonumber\] es un producto de tres enteros consecutivos. Como hemos visto en el Problema 4, cualquiera de tres enteros consecutivos deben contener un múltiplo de 3. De ello se deduce que su producto es también un múltiplo de 3.
- Caso 1: si\(n\bmod3=0\), entonces\(n=3q\) para algún entero\(q\), y\[n^3-n = (3q)^3-3q = 27q^3-3q = 3(9q^2-q), \nonumber\] donde\(9q^2-q\) es un entero.
- Caso 2: si\(n\bmod3=1\), entonces\(n=3q+1\) para algún entero\(q\), y\[n^3-n = (3q+1)^3-(3q+1) = 27q^3+27q^2+6q = 3(9q^3+9q^2+2q), \nonumber\] donde\(9q^3+9q^2+2q\) es un entero.
- Caso 2: si\(n\bmod3=2\), entonces\(n=3q+2\) para algún entero\(q\), y\[n^3-n = (3q+2)^3-(3q+2) = 27q^3+54q^2+33q+6 = 3(9q^3+18q^2+11q+2), \nonumber\] donde\(9q^3+18q^2+11q+2\) es un entero.
- Dejar\(n\) ser cualquier entero. Entonces\(n\bmod3=0,1,2\).
-
- \(s+t\)
- 4
Sección 5.3
- Asumir\(a\mid b\) y\(c\mid (-a)\). Existen enteros\(x\) y\(y\) tal que\(b=ax\) y\(-a=cy\). Entonces\[b = ax = (-a)(-x) = cy\cdot(-x) = (-c)\cdot xy, \nonumber\] donde\(xy\) es un entero. Así,\((-c)\mid b\).
- Hay tres casos, dependiendo del resto cuando un entero se divide por 3.
- \((3q)^2 = 9q^2 = 3\cdot3q^2\).
- \((3q+1)^2 = 9q^2+6q+1 = 3(3q^2+2q)+1\).
- \((3q+2)^2 = 9q^2+12q+4 = 9q^2+12q+3+1 = 3(3q^2+4q+1)+1\).
En cada caso, hemos demostrado que el cuadrado de un entero es de la forma\(3k\) o\(3k+1\).
Sección 5.4
-
- \(1\cdot 27+ 0\cdot 81= 27\)
- \(-3\cdot 24+ 1\cdot 84= 12\)
- \(-35\cdot1380+16\cdot3020= 20\)
- 1, 2, 17 y 34.
Sección 5.5
- Ya que\[-3\cdot(2n+1)+2\cdot(3n+2) = 1, \nonumber\] deducimos eso\(\gcd(2n+1,3n+2)=1\).
- Dejar\(a\),\(b\), y\(c\) ser enteros positivos tales que\(a\mid c\),\(b\mid c\), y\(\gcd(a,b)=1\). Entonces existen enteros\(x\) y\(y\) tal que\(c=ax\) y\(c=by\); y existen enteros\(s\) y\(t\) tal que\(sa+tb=1\). De ello se deduce que\[c = c\cdot 1 = c(sa+tb) = csa+ctb. \nonumber\] Usando\(c=ax\) y\(c=by\), encontramos\[c = csa+ctb = by\cdot sa+ax\cdot tb = ab(ys+xt), \nonumber\] donde\(ys+xt\) es un entero. Así,\(ab\mid c\).
Sección 5.6
-
- \(3^2\cdot5^2\cdot7\)
- \(2\cdot3^2\cdot7^2\cdot11\)
-
- 81
- 168
- Cada 50 días.
- Asumir\(x\in 10\mathbb{Z}\cap15\mathbb{Z}\), entonces\(x\in10\mathbb{Z}\) y\(x\in15\mathbb{Z}\). Esto significa que\(x\) es un múltiplo tanto de 10 como de 15. En consecuencia,\(x\) es un múltiplo de\(\text{lcm}(10,15)=30\), lo que significa\(x\in30\mathbb{Z}\). Así,\(10\mathbb{Z}\cap15\mathbb{Z} \subseteq 30\mathbb{Z}\).
A continuación, supongamos\(x\in 30\mathbb{Z}\), entonces\(x\) es un múltiplo de 30. En consecuencia,\(x\) es un múltiplo de 10, así como un múltiplo de 15. Esto significa\(x\in10\mathbb{Z}\), y\(x\in15\mathbb{Z}\). Como resultado,\(x\in 10\mathbb{Z}\cap15\mathbb{Z}\). Así,\(30\mathbb{Z} \subseteq 10\mathbb{Z}\cap15\mathbb{Z}\). Junto con\(10\mathbb{Z}\cap15\mathbb{Z} \subseteq 30\mathbb{Z}\), concluimos que\(10\mathbb{Z}\cap15\mathbb{Z} = 30\mathbb{Z}\).
-
- Cuando\(p\) se divide por 4, su resto es 0, 1, 2 o 3. Pero\(p\) es impar, por lo tanto,\(p\) es de la forma\(4k+1\) o\(4k+3\) para algún entero\(k\). Ya que\(p\geq3\), también necesitamos\(k\) ser un entero no negativo.
- Cuando\(p\) se divide por 6, su resto es 0, 1, 2, 3, 4 o 5. Pero\(p\) es extraño, por lo tanto,\(p\) es de la forma\(6k+1\),\(6k+3\), o\(6k+5\). Descartamos la forma\(6k+3\) porque esto haría\(p\) un múltiplo de 3. De ahí,\(p\) es de la forma\(6k+1\) o\(6k+5\) para algún entero no negativo\(k\).
Sección 5.7
- A continuación se\(\mathbb{Z}_8\) enumeran las tablas de suma y multiplicación para. \[\begin{array}{|c|c|c|c|c|c|c|c|}\hline + & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline\hline 0 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 1 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 0 \\ \hline 2 & 2 & 3 & 4 & 5 & 6 & 7 & 0 & 1 \\ \hline 3 & 3 & 4 & 5 & 6 & 7 & 0 & 1 & 2 \\ \hline 4 & 4 & 5 & 6 & 7 & 0 & 1 & 2 & 3 \\ \hline 5 & 5 & 6 & 7 & 0 & 1 & 2 & 3 & 4 \\ \hline 6 & 6 & 7 & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline 7 & 7 & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline \end{array} \qquad\qquad \begin{array}{|c|c|c|c|c|c|c|c|}\hline \cdot & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 1 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 2 & 0 & 2 & 4 & 6 & 0 & 2 & 4 & 6 \\ \hline 3 & 0 & 3 & 6 & 1 & 4 & 7 & 2 & 5 \\ \hline 4 & 0 & 4 & 0 & 4 & 0 & 4 & 0 & 4 \\ \hline 5 & 0 & 5 & 2 & 7 & 4 & 1 & 6 & 3 \\ \hline 6 & 0 & 6 & 4 & 2 & 0 & 6 & 4 & 2 \\ \hline 7 & 0 & 7 & 2 & 5 & 4 & 3 & 2 & 1 \\ \hline \end{array} \nonumber\]Sólo 1, 3, 5 y 7 tienen inversos multiplicativos. De hecho,\(1^{-1}=1\),\(3^{-1}=3\),\(5^{-1}=5\), y\(7^{-1}=7\).
- La suma es 9, y el producto es 7.
- A partir del siguiente cómputo\[\begin{array}{|c|l|} \hline \mbox{$m$ (mod~7)} & \hfil\mbox{$m^2+1$ (mod~7)} \\ \hline 0 & 0^2+1 = 1 \\ \pm1 & 1^2+1 = 2 \\ \pm2 & 2^2+1 = 5 \\ \pm3 & 3^2+1 = 10 \equiv 3 \\ \hline \end{array} \nonumber\] determinamos que\(m^2+1\not\equiv0\) (mod 7). Por lo tanto, no\(m^2+1\) es un múltiplo de 7 para todos los enteros\(m\).
- Ambos métodos\(4^{45}=1\) ceden\(\mathbb{Z}_{11}\).
-
- 9
Sección 6.1
- -24pt\(\begin{array}[t]{|c||*{6}{c|}} \hline x & 5.7 & \pi & e & -7.2 & -0.8 & 9 \\ \hline \lfloor x \rfloor & 5 & 3 & 2 & -8 & -1 & 9 \\ \lceil x \rceil & 6 & 4 & 3 & -7 &\phantom{-}0 & 9 \\ {[x]} & 6 & 3 & 3 & -7 & -1 & 9 \\ \hline \end{array}\)
- \([0,\infty)\).
Sección 6.2
- \(\big[\frac{7}{3},\infty\big)\).
- Sólo\(g\) es una función bien definida. La imagen\(f(4)\) es indefinida, y hay dos valores para\(h(3)\). De ahí que ambas\(f\) y no\(h\) sean funciones bien definidas.
-
- Sí, porque nunca ocurrirá ninguna división por cero.
- \(\begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline p(x) & 3 & 1 & 2 & 2 \\ \hline \end{array}\)\(\begin{array}{|c||c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline q(x) & 2 & 3 & 1 & 3 \\ \hline \end{array}\)
-
- 7
- 7
- 3
Sección 6.3
-
- No. Por ejemplo,\(f(0)=f(2)=1\).
- Sí, ya que\(g'(x)=3x^2-4x=x(3x-4)>0\) para\(x>2\).
- Debido a que el dominio y el codominio son intervalos semiabiertos, debemos tener cuidado con la inclusión y exclusión de los puntos finales. Podemos usar la gráfica que se muestra a continuación a la izquierda.
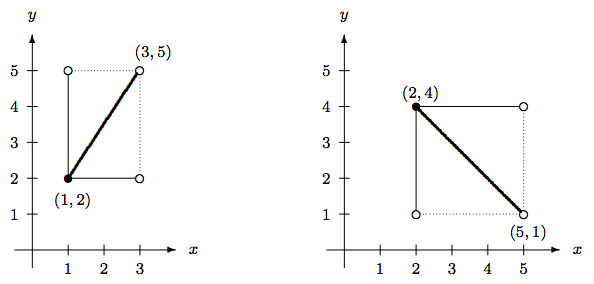
Nos encontramos\(f(x) = \frac{3}{2}\,x+\frac{1}{2}\).
-
- Uno a uno
- No uno a uno
-
- No uno a uno
- Uno a uno
- Hay doce funciones uno a uno de\(\{1,2\}\) a\(\{a,b,c,d\}\). A continuación se enumeran las imágenes de 1 y 2 debajo de ellas. \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7 & f_8 & f_9 & f_{10} & f_{11} & f_{12} \\ \hline\hline 1 & a & a & a & b & b & b & c & c & c & d & d & d \\ \hline 2 & b & c & d & a & c & d & a & b & d & a & b & c \\ \hline \end{array} \nonumber\]
-
- Uno a uno
- No uno a uno
- No uno a uno
Sección 6.4
-
- ¡Sí! No es fácil de expresar\(x\) en términos de a\(y\) partir de la ecuación\(y=x^3-2x^2+1\). No obstante, a partir de su gráfica, podemos decir que los\(y\) -valores cubren todos los posibles valores reales en el codominio.
- No, porque\(g(x)\geq1\).
-
- No en
- Sobre
-
- No en
- Sobre
- No, porque tenemos como máximo dos imágenes distintas, pero el codominio tiene cuatro elementos.
-
- Sobre
- No en
- No en
Sección 6.5
-
- \(f_1(A)=\{a,b\}\),\(f_1^{-1}(B)=\{2,3,4,5\}\)
- \(f_2(A)=\{a,c\}\),\(f_2^{-1}(B)=\{2,4\}\)
- \(f_3(A)=\{b,d\}\),\(f_3^{-1}(B)=\emptyset\)
- \(f_4(A)=\{e\}\),\(f_4^{-1}(B)=\{5\}\)
- Las imágenes de\(s\) se tabulan a continuación. \[\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|} \hline x & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 \\ \hline s(x) & 7 & 11 & 3 & 7 & 11 & 3 & 7 & 11 & 3 & 7 & 11 & 3 \\ \hline \end{array} \nonumber\]
- \(\{3,11\}\)
- \(\{0,3,6,9\}\)
- \(\{3,7,11\}\)
-
- \([20,26)\);\(\{20,23,26\}\)
- \([-3,-\frac{4}{3}\big)\);\(\{-2\}\)
-
- \(\big\{\frac{3}{5},\frac{9}{5},\frac{27}{5}, 3,9,27,15,45,135\big\}\)
- \(\{(-3,2)\}\)c)\(\mathbb{N}\times\{0\}\)
- Para que una función esté bien definida, cada suma de fila debe ser 1. Para que la función sea uno a uno, cada suma de columna debe ser como máximo 1. Para que la función esté en, cada suma de columna debe ser al menos 1 (por lo tanto, ninguna suma de columna es cero).
- Vamos\(y\in f(C_1)-f(C_2)\), queremos demostrarlo\(y\in f(C_1-C_2)\) también. Ya que\(y\in f(C_1)-f(C_2)\), sabemos que existe\(x\in A\) tal que\(f(x)=y\). Tener\(y\in f(C_1)-f(C-2)\) medios\(y\in f(C_1)\) pero\(y\notin f(C_2)\). De ahí,\(x\in C_1\) pero\(x\notin C_2\). En otras palabras,\(x\in C_1-C_2\). Esto lleva a\(y=f(x)\in f(C_1-C_2)\). Esto completa la prueba de que\(f(C_1)-f(C_2) \subseteq f(C_1-C_2)\).
- \(\{0,1,4,9\}\);\(\{0,\pm1,\pm2,\pm3\}\).
Sección 6.6
- Sólo (e) es biyectiva.
- Sus funciones inversas\({f^{-1},g^{-1}}:{(4,7)}\to{(1,3)}\) están definidas por\[f^{-1}(x) = \frac{2}{3}\left(x-\frac{ 5}{2}\right), \qquad\mbox{and}\qquad g^{-1}(x) = -\frac{2}{3}\left(x-\frac{17}{2}\right). \nonumber\]
- \({g^{-1}}:\to{[4,7]}{[1,3]}\), donde\(g^{-1}(x) = \cases{ x-3 & if $4\leq x <5$, \cr \frac{1}{2} (11-x) & if $5 \leq x \leq 7$. \cr}\)
- \({s^{-1}}:{(-\infty,-3)}\to{\mathbb{R}}\), donde\(s^{-1}(x) = \frac{1}{2}\, \ln\left(\frac{4-x}{7}\right)\).
-
- \({u^{-1}}:{\mathbb{Q}}\to{\mathbb{Q}}\),\(u^{-1}(x)=(x+2)/3\)
- Las imágenes debajo\({\alpha^{-1}}:{\{a,b,c,d,e,f,g,h\}}\to {\{1,2,3,4,5,6,7,8\}}\) se dan a continuación. \[\begin{array}{|c||*{8}{c|}} \hline x & a & b & c & d & e & f & g & h \\ \hline \alpha^{-1}(x)& 2 & 5 & 8 & 3 & 6 & 7 & 1 & 4 \\ \hline \end{array} \nonumber\]
Sección 6.7
- Ambos\(f\circ g\) y\(g\circ f\) son de\(\mathbb{R}\) a\(\mathbb{R}\), dónde\((f\circ g)(x)=15x^2+19\), y\((g\circ f)(x)=75x^2-30x+7\).
- No necesitamos encontrar la fórmula de la función compuesta, ya que podemos evaluar el resultado directamente:\(f(g(f(0))) = f(g(1)) = f(2) = -5\).
-
- \({g\circ f}:{\mathbb{Z}}\to{\mathbb{Q}}\),\((g\circ f)(n)=1/(n^2+1)\)
- \({g\circ f}:{\mathbb{R}}\to{(0,1)}\),\((g\circ f)(x)=x^2/(x^2+1)\)
-
- \(\begin{array}{l} {g\circ f}:{\{1,2,3,4,5\}}\to{\{1,2,3,4,5\}}, \\ \phantom{(a)} (g\circ f)(1)=2, (g\circ f)(2)=5, (g\circ f)(3)=1, (g\circ f)(4)=3, (g\circ f)(5)=4 \end{array}\)
- \({g\circ f}:{\mathbb{Z}}\to{\mathbb{Z}}\),\((g \circ f)(n) = \cases{ 3(2n-1) & if $n\geq 0$, \cr 2n+1 & if $n < 0$. \cr}\)
-
- \(\begin{array}{ll}{f\circ g}:{\mathbb{Z}}\to{\mathbb{Z}}, & (f\circ g)(n) = 3-n \\ \phantom{(a)} {(f\circ g)^{-1}}:{\mathbb{Z}}\to{\mathbb{Z}}, & (f\circ g)^{-1}(n) = 3-n \\ \phantom{(a)} {f^{-1}:}{\mathbb{Z}}\to{\mathbb{Z}}, & f^{-1}(n) =2-n \\ \phantom{(a)} {g^{-1}}:{\mathbb{Z}}\to{\mathbb{Z}}, & g^{-1}(n) = n-1 \\ \phantom{(a)} {g^{-1}\circ: f^{-1}}{\mathbb{Z}}\to{\mathbb{Z}}, & (g^{-1}\circ f^{-1})(n) = 3-n \end{array}\)
Sección 7.1
-
-
\(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 6 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 6 \end{array} & \left(\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right) \end{array}\)
-
\(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 6 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 6 \end{array} & \left(\begin{array}{cccc} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \end{array}\right) \end{array}\)
-
\(\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 6 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 6 \end{array} & \left(\begin{array}{cccc} 0 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{array}\right) \end{array}\)
-
-
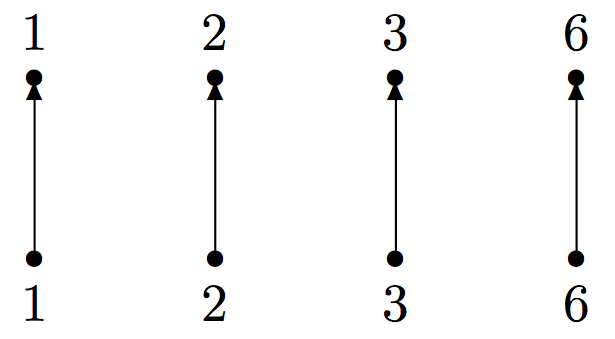
- \(\mbox{domain}=\mbox{image}=\{1,2,3,6\}\).
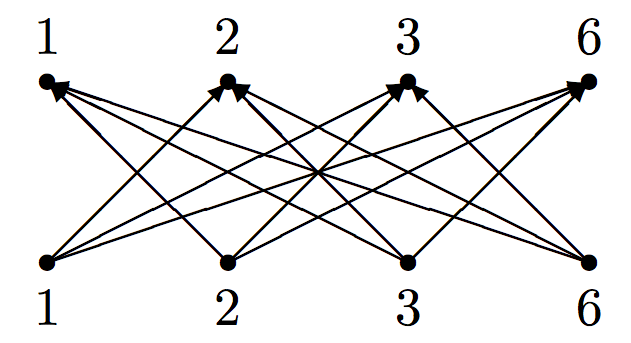
- \(\mbox{domain}=\mbox{image}=\{1,2,3,6\}\).
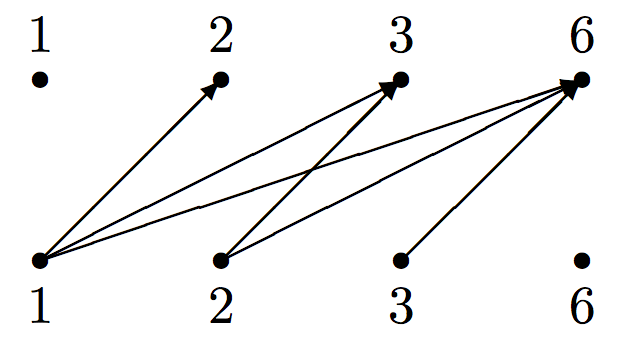
- \(\mbox{domain}=\{1,2,3\}\),\(\mbox{image}=\{2,3,6\}\).
-
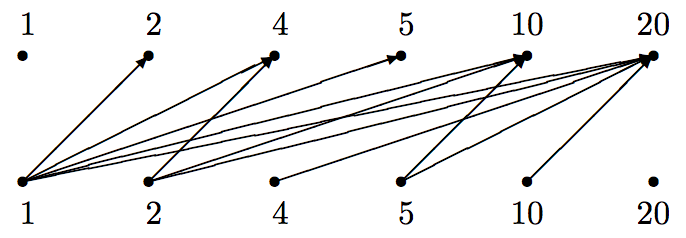
\(\begin{array}[t]{cc} & \begin{array}{cccccc} 1 & 2 & 4 & 5 & 10 & 20 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 4 \\ 5 \\ 10 \\ 20 \end{array} & \left(\begin{array}{cccccc} 0 & 1 & 1 & 1 &\; 1 \;&\; 1 \\ 0 & 0 & 1 & 0 &\; 1 \;&\; 1 \\ 0 & 0 & 0 & 0 &\; 0 \;&\; 1 \\ 0 & 0 & 0 & 0 &\; 1 \;&\; 1 \\ 0 & 0 & 0 & 0 &\; 0 \;&\; 1 \\ 0 & 0 & 0 & 0 &\; 0 \;&\; 0 \end{array}\right) \end{array}\)
- \(\begin{array}[t]{cc} & \begin{array}{cccc} \;\;\;\;\emptyset & \{1\} & \{2\} & \{1,2\} \end{array} \\ \begin{array}{c} \emptyset \\ \{1\} \\ \{2\} \\ \{1,2\} \end{array} & \left(\begin{array}{cccc} 0 &\;\;0\;&\;\;0&\;\;\;0 \\ 0 &\;\;1\;&\;\;0&\;\;\;1 \\ 0 &\;\;0\;&\;\;1&\;\;\;1 \\ 0 &\;\;1\;&\;\;1&\;\;\;1 \end{array}\right) \end{array}\)
Sección 7.2
-
- Reflexiva, simétrica, antisimétrica y transitiva.
- Irreflexiva y simétrica.
- Irreflexiva y transitiva.
-
- Antisimétrico.
- Refleja, simétrica y transitiva.
- Irreflexiva, simétrica y transitiva.
- Refleja, simétrica y transitiva.
- Antisimétricos y transitivos.
- Irreflexivo y antisimétrico.
- Simétrico.
-
- \(A\)no es reflexivo porque\((X,X)\notin A\) si\(X\neq\emptyset\).
- \(A\)no es irreflexivo porque\((\emptyset,\emptyset)\in A\).
- No. Por ejemplo, considere\(S=\{a,b,c\}\),\(X=\{a\}\),\(Y=\{b\}\), y\(Z=\{a,c\}\). Entonces\((X,Y)\in A\),\((Y,Z)\in A\), pero\((X,Z)\notin A\).
-
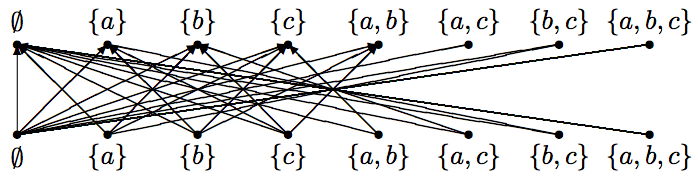
\(\begin{array}[t]{cc} & \begin{array}{cccccccc} \emptyset & \{a\} & \{b\} & \{c\} & \{a,b\} & \{a,c\} & \{b,c\} & \{a,b,c\} \end{array} \\ \begin{array}{c} \emptyset \\ \{a\} \\ \{b\} \\ \{c\} \\ \{a,b\} \\ \{a,c\} \\ \{b,c\} \\ \{a,b,c\} \end{array} & \left(\begin{array}{cccccccc} 1 & \phantom{a} 1 \phantom{a} & \phantom{a} 1 \phantom{a} & \phantom{a} 1 \phantom{a} & \phantom{(a} 1 \phantom {a)} & \phantom{a)} 1 \phantom{a)} & \phantom{a)} 1 \phantom{a)} & \phantom{(aa} 1 \phantom{(aa} \\ 1 & 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \end{array}\)
-
- Simétrico.
- Reflexiva y simétrica.
-
- Reflexiva, antisimétrica y transitiva.
- Refleja, simétrica y transitiva.
- Simétrico.
-
- Reflexiva, antisimétrica y transitiva.
- Simétrico.
- Simétrica y transitiva.
-
- Reflexiva y transitiva.
- Simétrico,
- Refleja, simétrica y transitiva.
-
- Simétrica y transitiva.
- Refleja, simétrica y transitiva.
- Reflexiva y transitiva.
Sección 7.3
-
- Las clases de equivalencia son de la forma\(\{3-k,3+k\}\) para algún entero\(k\). Por ejemplo,\([3]=\{3\}\),\([2]=\{2,4\}\),\([1]=\{1,5\}\), y\([-5]=\{-5,11\}\).
- Hay tres clases de equivalencia:\([0]=3\mathbb{Z}\),\([1]=1+3\mathbb{Z}\), y\([2]=2+3\mathbb{Z}\).
-
- Cierto
- Falso
- \([\{1,5\}] = \big\{ \{1\}, \{1,2\}, \{1,4\}, \{1,5\}, \{1,2,4\}, \{1,2,5\}, \{1,4,5\}, \{1,2,4,5\} \big\}\)
- \([X] = \{(X\cap T)\cup Y \mid Y\in\wp(\overline{T})\}\). En otras palabras,\(S\sim X\) si\(S\) contiene el mismo elemento en\(X\cap T\), más posiblemente algunos elementos no en\(T\).
-
- Sí, con\([(a,b)] = \{(x,y) \mid y=x+k \text{ for some constant } k\). Es decir, las clases de equivalencia son las líneas rectas de la forma\(y=x+k\) para alguna constante\(k\).
- No. Por ejemplo,\((2,5)\sim(3,5)\) y\((3,5)\sim(3,7)\), pero\((2,5)\not\sim(3,7)\). De ahí que la relación no\(\sim\) sea transitiva.
- Nos encontramos\([0] = \frac{1}{2}\,\mathbb{Z} = \{\frac{n}{2} \mid n\in\mathbb{Z}\}\), y\([\frac{1}{4}] = \frac{1}{4}+\frac{1}{2}\,\mathbb{Z} = \{\frac{2n+1}{4} \mid n\in\mathbb{Z}\}\).
Sección 7.4
- A continuación se muestra el diagrama de Hasse.
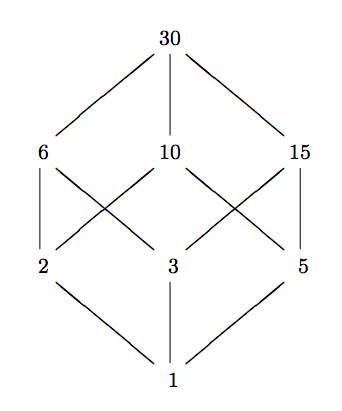
- Vamos\(a\in B\), ya que\(B\subseteq A\), también nos encontramos\(a\in A\). Ya que\((A,\preceq)\) es un poset, la relación\(\preceq\) sobre\(A\) es reflexiva, por lo tanto,\(a\preceq a\). Esto demuestra que\(\preceq\) sigue siendo reflexivo cuando se restringe a\(B\). La antisimetría y la transitividad se prueban con un argumento similar.
-
- A continuación se muestra el diagrama de Hasse.
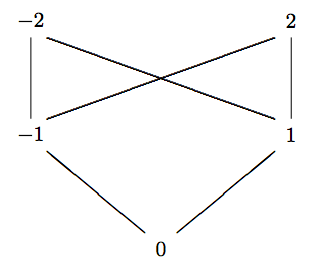
Copiar y Pegar Leyenda aquí
- A continuación se muestra el diagrama de Hasse.
- \(B=\big\{\emptyset,\{a\},\{a,b\},\{a,b,c\},\{a,b,c,d\}\big\}\).
Sección 8.2
- 6.
- 70.
- \(7\cdot5+7\cdot4+5\cdot4\)
- \(4^5\),\(4^5-3\cdot4^2\)
-
- \(52^4\)
- \(39^4\)
- \(4\cdot13^4\)
- \(4\cdot48\cdot52^3\)
- \(52^4-48^4\)
-
- \(9\cdot10^3\)
- \(8\cdot9^3\)
- \(9\cdot10^3-8\cdot9^3\)
- \(9\cdot10\)
-
- \(8^6\)
- \(8\cdot7\cdot6\cdot5\cdot4\cdot3\)
- 0
- \(8^6-4^6\)
- \(4\cdot8^4\)f)\(7^5\)
Sección 8.3
- \(62^8\),\(P(62,8)\).
- \(P(14,5)\).
- \(p(7,3)\cdot P(10,3) + P(7,3)\cdot P(11,3) + P(10,3)\cdot P(11,3)\).
- \(P(11,7)\cdot3!/7\).
Sección 8.4
- \(\binom{6}{3}\binom{8}{3}\).
-
- al menos 5
- al menos 7
- 10.
-
- \(\binom{14}{4}\)
- \(\binom{14}{4}-\binom{11}{4}\)
- \(\binom{3}{2}\binom{7}{1}\binom{4}{1} +\binom{3}{1}\binom{7}{2}\binom{4}{1} +\binom{3}{1}\binom{7}{1}\binom{4}{2}\)
-
- \(8!\)
- \(\binom{8}{2}\,P(8,2)\, \big[\binom{6}{2}\,P(8,2)+2\cdot7\cdot6\cdot7+7\cdot6\big]\)
- \(\binom{16}{7}\).
-
- \(\binom{52}{5}\)
- \(4 \,\binom{13}{2}\,13^3\)
- \(13\,\binom{4}{2}\binom{12}{3}\,4^3\)
- \(13\,\binom{4}{3}\binom{12}{2}\,4^2\)
- \(13\,\binom{4}{3}\,12\,\binom{4}{2}\)
- \(10\cdot(4^5-1)\)
- \(4\,\big[\binom{13}{5}-10\big]\)
- \(4\cdot10\)
Sección 8.5
-
- \(x^5+5x^4y+10x^3y^2+10x^2y^3+5xy^4+y^5\)
- \(s^6-6s^5t+15s^4t^2-20s^3t^3+15s^2t^4-6st^5+t^6\)
- \(a^4+12a^3b+54a^2b^2+108ab^3+81b^4\)
-
- \(\binom{4}{2}=6\)
- \(-\binom{9}{3}\,3^6\left(\frac{2}{5}\right)^3 =-\frac{489888}{125}\)
- 0
- \(-\binom{6}{3}\,3^3\left(\frac{5}{7}\right)^3 =-\frac{67500}{343}\)
- \(\sum_{k=0}^n \binom{n}{k} r^k = (1+r)^n\)
-
- \(k^2 = 2\binom{k}{2} + \binom{k}{1}\)
- \(\sum_{k=1}^n k^2 = \frac{1}{6}\,n(n+1)(2n+1)\)

