3.6: Funciones

Un tipo de relación muy, muy importante se llama función. Algunos matemáticos tratan las funciones totalmente separadamente de las relaciones, pero creo que es más útil pensar en una función como un tipo especial de relación. Muchas de las ideas son las mismas, como verás.

Piensa en las relaciones entre magos y refrescos. Una de esas relaciones (la llamamos\(R\)) tenía (Harry, Mt. Rocío) y (Ron, Mt. Rocío) en ella. Otro (\(S\)) contenía (Hermione, Mt. Rocío), (Hermione, Dr. Pepper) y (Harry, Dr. Pepper). Como había tres magos y dos refrescos, calculamos que había\(2^6\) tales relaciones.

Ahora algunas de esas relaciones tienen exactamente un par ordenado por cada mago. Por ejemplo, la relación\(F\) que contiene {(Harry, Dr. Pepper), (Ron, Mt. Rocío), (Hermione, Mt. Rocío)}. Este tipo de relación es una función. Asocia cada elemento del primer conjunto exactamente con un elemento del segundo conjunto. Obviamente no todas las relaciones son funciones:\(R\), por ejemplo, no es (no hay pareja con Hermione) y tampoco lo es\(S\) (hay más de un par con Hermione). Pero aquellos que sí forman una clase de interés muy especial, y justifican una terminología completamente nueva.

Cuando tenemos una función\(F\) entre un conjunto\(X\) y\(Y\), escribimos\(F : X \rightarrow Y\) para indicar esto. El conjunto\(X\) se llama el dominio de la función, y el conjunto\(Y\) se llama codominio. Los dos puntos y la flecha están ahí para completar la sintaxis. La regla con funciones es muy simple: cada elemento del dominio está relacionado exactamente con un elemento del codominio. A veces decimos que un elemento de dominio es “mapeado" a su elemento de codominio correspondiente. Obsérvese con mucho cuidado que lo contrario no es necesariamente cierto. De hecho, con el ejemplo de magos y bebidas, no puede ser cierto: hay menos bebidas que magos, por lo que alguna bebida está destinada a estar relacionada con más de un mago. (Piénsalo.) También es perfectamente legítimo tener una función como {(Harry, Dr. Pepper), (Ron, Dr. Pepper), (Hermione, Dr. Pepper)}, donde algunos elementos del codominio quedan fuera por completo.

Una de las cosas que hace que las funciones sean útiles es que podemos preguntar “¿qué elemento de\(Y\) va con\(X\)?” y siempre vamos a recuperar una respuesta bien definida. Realmente no podemos hacer eso con las relaciones en general, porque la respuesta podría ser “ninguna” o “varias”. Echa un vistazo a los\(S\) ejemplos\(R\) y, arriba: ¿qué respuesta obtendríamos si preguntáramos “¿a qué bebida va el mapa de Hermione?” para cualquiera de las relaciones? Respuesta: no hay respuesta.

Pero con funciones, puedo hacer esa pregunta libremente porque sé que voy a obtener una respuesta kosher. Con\(F\), puedo preguntar, “¿a qué bebida mapea Hermione?” y la respuesta es “Mt. Rocío”. En símbolos, escribimos esto de la siguiente manera:

\(F\)(Hermione) = Mt. Rocío

Esto le resultará familiar a los programadores informáticos, ya que se asemeja a una llamada de función. De hecho, se trata de una llamada de función. Eso es exactamente lo que es. Las “funciones” en lenguajes como C++ y Java fueron de hecho nombradas después de esta noción matemática discreta. Y si sabes algo de programación, sabes que en un programa puedo “llamar a la función F ()” y “pasarle el argumento 'Hermione'” y “obtener el valor de retorno 'Mt.Dew.'” Nunca tengo que preocuparme por recuperar más de un valor, o no obtener ninguno en absoluto.

Quizás también recuerdes haber discutido funciones en matemáticas de secundaria, y la llamada “prueba de línea vertical”. Cuando trazó los valores de una función numérica en una gráfica, y no había una línea vertical (arriba y abajo) que intersectara más de un punto, podría llamar a la gráfica de forma segura una “función”. Eso es realmente exactamente lo mismo que la condición que acabo de dar para las funciones, declaró gráficamente. Si una gráfica pasa la prueba de línea vertical, entonces no hay ningún\(x\) valor para el que haya más de un\(y\) valor. Esto significa que tiene sentido preguntar “¿cuál es el valor de\(y\) para un valor particular de\(x\)?” Siempre obtendrás una y sólo una respuesta. (Por supuesto, no existe tal cosa como una “prueba de línea horizontal”, ya que las funciones son libres de mapear más de un\(x\) valor al mismo\(y\) valor. Simplemente no pueden hacer lo contrario.)

La diferencia entre las funciones de las matemáticas de secundaria y las funciones de las que estamos hablando aquí, por cierto, es simplemente que nuestras funciones no son necesariamente numéricas. A veces dibujamos una especie de “tramas”, sin embargo, como esta:

Figura\(\PageIndex{1}\): Una función representada gráficamente.

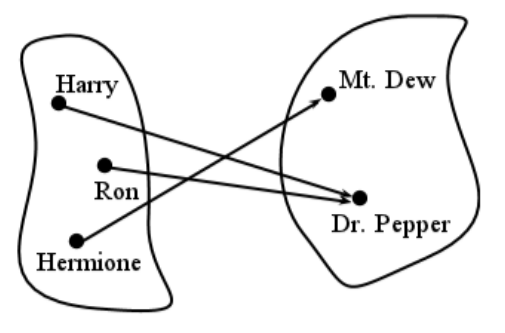
Esto simplemente muestra qué elementos del dominio mapean a qué elementos del codominio. El blob izquierdo es el dominio, el blob derecho es el codominio, y hay una flecha que representa cada mapeo.

Ahora como con las relaciones, las funciones normalmente tienen “sentido”. Podríamos definir una función llamada “FirstTaste” que asocia a cada mago con el refresco que primero probó cuando era niño. Podríamos definir otro llamado “FaveDrink” que mapee a cada mago a su favorito, presumiendo que cada mago tiene una bebida favorita en el set (Hermione tendrá que pasar por alto su té helado y elegir entre las opciones proporcionadas). Una tercera función llamada “WouldChoosewithMexicanFood” proporciona información sobre qué bebida proporciona cada mago con ese tipo de cocina. Aquí están los valores de Ron para cada una de las tres funciones:

PrimeroCatado (Ron) = Mt. Dew
FaveDrink (Ron) = Mt.
Rocío elegiríaConcomida Mexicana (Ron) = Dr. Pepper

Estos valores indican que Mt. Dew fue el soda pop que Ron primero bebió, y desde entonces ha sido su favorito, aunque en La Estrellita prefiere un Pepper.

Las funciones se pueden definir de manera intensiva o extensiva, al igual que con las relaciones. Intensivamente, proporcionamos el significado conceptual de lo que representa la función. Extensionalmente, enumeramos los valores para cada elemento del dominio.

Otro término que se aplica a cada función es su rango. El rango de una función es el subconjunto del codominio al que al menos un elemento al que realmente se asigna el dominio. Es la parte del codominio que es “alcanzable”. Por ejemplo, si la función\(G : X \rightarrow Y\) es {(Harry, Dr. Pepper), (Ron, Dr. Pepper), (Hermione, Dr. Pepper)}, entonces a pesar de que el codominio es {Dr. Pepper, Mt. Rocío} el rango es meramente {Dr. Pepper}. Eso es porque no hay ningún par ordenado que contenga Mt. Rocío, por lo que queda fuera del rango. No se puede “alcanzar” el monte. Rocíe a través de la\(G\) función comenzando con cualquiera de sus entradas, por lo que se deja afuera en el frío.

Por cierto, el rango de una función a veces se llama su imagen. Estos términos son sinónimos.