1: Aritmética IEEE
- Page ID
- 117227
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Definiciones
La línea real es continua, mientras que los números de computadora son discretos. Aquí aprendemos cómo se representan los números en la computadora y cómo esto puede conducir a errores de redondeo. Un número se puede representar en la computadora como un entero con signo o sin signo, o como un número real (punto flotante). Presentamos las siguientes definiciones:
\(\begin{array}{lll}\text { Bit } & =0 \text { or } 1 & \\ \text { Byte } & =8 \text { bits } & \\ \text { Word } & =\text { Reals: } & 4 \text { bytes (single precision) } \\ & & 8 \text { bytes (double precision) } \\ & =\text { Integers: } & 1,2,4, \text { or } 8 \text { byte signed } \\ & & 1,2,4, \text { or } 8 \text { byte unsigned }\end{array}\)
Normalmente, la computación científica en MATLAB es de doble precisión utilizando números reales de 8 bytes. La precisión única se puede usar con poca frecuencia en problemas grandes para conservar la memoria. Los enteros también se pueden usar con poca frecuencia en situaciones especiales. Dado que la doble precisión es el valor por defecto -y lo que se utilizará en esta clase- nos centraremos aquí en su representación.
Formato IEEE de doble precisión
La doble precisión hace uso de palabras de 8 bytes (64 bits), y generalmente da como resultado cálculos suficientemente precisos. El formato para un número de doble precisión es

\[ \nonumber \#=(-1)^s \times 2^{e-1023} \times 1.f, \nonumber \]
donde\(\mathrm{s}\) está el bit de signo, e es el exponente sesgado y 1.f (usando un punto binario) es el significado. Vemos que los 64 bits están distribuidos de manera que el signo usa 1 bit, el exponente usa 11 bits, y el significand usa 52 bits. La distribución de bits entre el exponente y el significando consiste en conciliar dos deseos contradictorios: que los números vayan desde valores muy grandes hasta valores muy pequeños, y que el espaciado relativo entre los números sea pequeño.
Números de máquina
Mostramos para ilustración cómo los números 1,2, y\(1 / 2\) se representan en doble precisión. Para el número 1, escribimos
\[1.0=(-1)^{0} \times 2^{(1023-1023)} \times 1.0 . \nonumber \]
De (1.1), encontramos\(\mathrm{s}=0, \mathrm{e}=1023\), y\(\mathrm{f}=0\). Ahora
\[1023=01111111111 \text { (base 2), } \nonumber \]
de manera que la representación de la máquina del número 1 viene dada por
\[0011111111110000 \ldots 0000 \text {. } \nonumber \]
Se puede ver la representación de la máquina de los números en MATLAB usando el comando format hex. MATLAB luego muestra el número hexadecimal correspondiente al número binario de máquina. Hex mapea números binarios de cuatro bits a un solo carácter, donde los números binarios correspondientes al decimal 0-9 se mapean a los mismos números decimales, y los números binarios correspondientes a\(10-15\) se mapean a a-f. Por lo tanto, la representación hexadecimal del número 1 dada por (1.3) viene dada por
\[3 f f 0\, 0000\, 0000\, 0000 \text {. } \nonumber \]
Para el número 2, tenemos
\[2.0=(-1)^{0} \times 2^{(1024-1023)} \times 1.0, \nonumber \]
con representación binaria
\[0100\, 0000\, 0000\, 0000 \ldots 0000 \nonumber \]
y representación hexadecimal
\[4000\, 0000\, 0000\, 0000 . \nonumber \]
Para el número\(1 / 2\), tenemos
\[2.0=(-1)^{0} \times 2^{(1022-1023)} \times 1.0, \nonumber \]
con representación binaria
\[0011\, 1111\, 1110\, 0000 \ldots 0000 \nonumber \]
y representación hexadecimal
\[4 \mathrm{fe} 0\, 0000\, 0000\, 0000 . \nonumber \]
Los números 1,2 y se\(1 / 2\) pueden representar exactamente en doble precisión. Pero los enteros muy grandes, y la mayoría de los números reales no pueden. Por ejemplo, el número\(1 / 3\) es inexacto, y así es\(1 / 5\), que consideramos aquí. Escribimos
\[\begin{aligned} \frac{1}{5} &=(-1)^{0} \times \frac{1}{8} \times\left(1+\frac{3}{5}\right) \\ &=(-1)^{0} \times 2^{1020-1023} \times\left(1+\frac{3}{5}\right) \end{aligned} \nonumber \]
de manera que\(\mathrm{s}=0, \mathrm{e}=1020=01111111100\) (base 2), y\(\mathrm{f}=3 / 5\). La razón 1/5 es inexacta es que\(3 / 5\) no tiene una representación finita en binario. Para convertir\(3 / 5\) a binario, multiplicamos sucesivamente por 2 de la siguiente manera:
\[ \begin{array}{lll} 0.6 \ldots & \qquad \qquad \qquad & 0. \\ 1.2 \ldots & \qquad \qquad \qquad & 0.1 \\ 0.4 \ldots & \qquad \qquad \qquad & 0.10 \\ 0.8 \ldots & \qquad \qquad \qquad & 0.100 \\ 1.6 \ldots & \qquad \qquad \qquad & 0.1001 \\ \qquad \text{etc} & & \end{array} \nonumber \]
de manera que\(3 / 5\) exactamente en binario es\(0 . \overline{1001}\), donde la barra denota una repetición sin fin. Con solo 52 bits para representar\(\mathrm{f}\), la fracción\(3 / 5\) es inexacta y tenemos
\[\mathrm{f}=10011001 \ldots 10011010 \text {, } \nonumber \]
donde hemos redondeado el extremo repetitivo del número\(\overline{1001}\) al número binario más cercano 1010. Aquí el redondeo es hacia arriba porque el 53-bit es un 1 seguido de no todos los ceros. Pero el redondeo también puede ser a la baja si el bit 53 es un 0. Exactamente en el límite (el 53-bit es un 1 seguido de todos los ceros), el redondeo es al número par más cercano. En esta situación especial que ocurre sólo en raras ocasiones, si el 52 bits es un 0, entonces el redondeo es hacia abajo, y si el bit 52 es un 1, entonces el redondeo es hacia arriba.
Por lo tanto, el número de máquina\(1 / 5\) se representa como
\[00111111110010011001 \ldots 10011010 \text {, } \nonumber \]
o en hex,
3fc99999999a
El pequeño error al representar un número como\(1 / 5\) en doble precisión generalmente hace poca diferencia en un cálculo. Uno suele estar satisfecho para obtener resultados precisos a unos pocos dígitos significativos. Sin embargo, los científicos computacionales necesitan ser conscientes de que la mayoría de los números no están representados exactamente.
Por ejemplo, considere restar lo que deberían ser dos números reales idénticos que no sean idénticos en la computadora. En MATLAB, si se entra en la línea de comandos
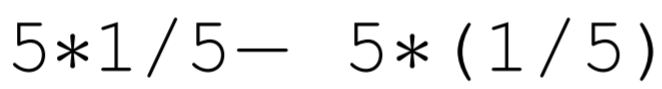
la respuesta resultante es 0, como cabría esperar. Pero si uno entra
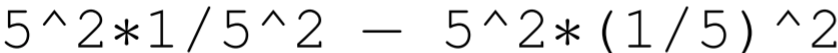
la respuesta resultante es\(-2.2204 \mathrm{e}-16\), un número ligeramente diferente a cero. La razón de este error es que aunque el número se\(5^{2} * 1 / 5^{2}=25 / 25=1\) puede representar exactamente, el número\(5^{2} *(1 / 5)^{2}\) es inexacto y ligeramente mayor que uno. Probar exactamente cero en un cálculo que depende de la cancelación de números reales, entonces, puede que no funcione. Más problemáticos, sin embargo, son los cálculos que restan dos números grandes con la esperanza de obtener un número pequeño y sensible. Se puede producir una pérdida total de precisión del número pequeño.
Números especiales
Tanto el exponente más grande como el más pequeño están reservados en la aritmética IEEE. Cuando\(\mathrm{f}=0\), el exponente más grande,\(\mathrm{e}=11111111111\), se utiliza para representar\(\pm \infty\) (escrito en MATLAB como Inf y - Inf). Cuando\(\mathrm{f} \neq 0\), el exponente más grande se usa para representar 'no un número' (escrito en MATLAB como NaN). La aritmética IEEE también implementa lo que se llama números denormales, también llamado subflujo agraciado. Se reserva el exponente más pequeño,\(\mathrm{e}=00000000000\), para representar números para los que la representación cambia de 1.f a\(0 . f\).
Con el mayor exponente reservado, el mayor número positivo de precisión doble tiene\(\mathrm{s}=0, \mathrm{e}=11111111110=2046\), y\(\mathrm{f}=11111111 \ldots 1111=1-2^{-52} .\) Llamado realmax en MATLAB, tenemos
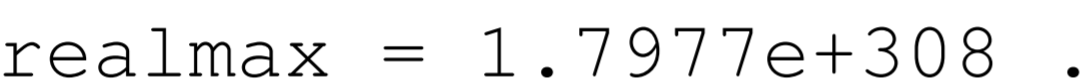
Con el exponente más pequeño reservado, el número de doble precisión positivo más pequeño tiene\(\mathrm{s}=0, \mathrm{e}=00000000001=1\), y\(\mathrm{f}=00000000 \ldots 0000=0\). Llamado realmin en MATLAB, tenemos

Por encima de realmax, uno obtiene Inf, y por debajo de realmin, uno obtiene primero números denormales y luego 0.
Otro número importante se llama machine epsilon (llamado eps en MATLAB). La máquina épsilon se define como la distancia entre 1 y el siguiente número más grande. Si\(0 \leq \delta<e p s / 2\), entonces\(1+\delta=1\) en computación matemática. También desde
\[x+y=x(1+y / x), \nonumber \]
si\(0 \leq y / x<e p s / 2\), entonces\(x+y=x\) en matemática informática.
Ahora, el número 1 en formato IEEE de doble precisión está escrito como
\[1=2^{0} \times 1.000 \ldots 0, \nonumber \]
con 520's siguiendo el punto binario. El número apenas mayor que 1 tiene un 1 en la posición 52 después del punto decimal. Por lo tanto,
\[\text { eps }=2^{-52} \approx 2.2204 e-016 \text {. } \nonumber \]
¿Cuál es la distancia entre 1 y el número apenas menor que 1? Aquí, el número apenas más pequeño que uno se puede escribir como
\[2^{-1} \times 1.111 \ldots 1=2^{-1}\left(1+\left(1-2^{-52}\right)\right)=1-2^{-53} \nonumber \]
Por lo tanto, esta distancia es\(2^{-53}=\mathrm{eps} / 2\).
Aquí, observamos que el espaciamiento entre números es uniforme entre potencias de 2, pero cambia en un factor de dos con cada potencia adicional de dos. Por ejemplo, el espaciado de números entre 1 y 2 es\(2^{-52}\), entre 2 y 4 es\(2^{-51}\), entre 4 y 8 es\(2^{-50}\), etc. ocurre una excepción para los números denormales, donde el espaciamiento se vuelve uniforme hasta llegar a cero. Los números denormales implementan un subflujo agraciado y no deben usarse para el cálculo normal.
Error de redondoff
Considera resolver la ecuación cuadrática
\[x^{2}+2 b x-1=0, \nonumber \]
donde\(b\) es un parámetro. La fórmula cuadrática produce las dos soluciones
\[x_{\pm}=-b \pm \sqrt{b^{2}+1} . \nonumber \]
Ahora, considere la solución con\(b>0\) y\(x>0\) (la\(x_{+}\) solución) dada por
\[x=-b+\sqrt{b^{2}+1} . \nonumber \]
Como\(b \rightarrow \infty\)
\[\begin{aligned} x &=-b+\sqrt{b^{2}+1} \\ &=-b+b \sqrt{1+1 / b^{2}} \\ &=b\left(\sqrt{1+1 / b^{2}}-1\right) \\ & \approx b\left(1+\frac{1}{2 b^{2}}-1\right) \\ &=\frac{1}{2 b} . \end{aligned} \nonumber \]
Ahora en doble precisión, realmin\(\approx 2.2 \times 10^{-308}\) y en software profesional uno quisiera\(x\) ser exacto a este valor antes de que pase a 0 vía números denormales. Por lo tanto, se\(x\) debe computar con precisión a\(b \approx 1 /(2 \times\) realmin\() \approx 2 \times 10^{307}\). ¿Qué pasa si calculamos (1.19) directamente? Entonces\(x=0\) cuando\(b^{2}+1=b^{2}\), o\(1+1 / b^{2}=1\). Por lo tanto,\(x=0\) cuando\(1 / b^{2}<\) eps\(/ 2\), o\(b>\sqrt{2 / e p s} \approx 10^{8}\).
La forma en que un diseñador de software matemático profesional resuelve este problema es computar la solución para\(x\)\(b>0\) cuando
\[x=\frac{1}{b+\sqrt{b^{2}+1}} . \nonumber \]
En esta forma, cuando\(b^{2}+1=b^{2}\), entonces\(x=1 / 2 b\), que es la forma asintótica correcta.


