7: Métodos iterativos

Los métodos iterativos se utilizan a menudo para resolver un sistema de ecuaciones no lineales. Incluso para sistemas lineales, los métodos iterativos tienen algunas ventajas. Pueden requerir menos memoria y pueden ser computacionalmente más rápidos. También son más fáciles de codificar. Aquí, sin detallar el análisis numérico teórico, simplemente explicaremos los métodos iterativos relacionados que van por los nombres del método Jacobi, el método Gauss-Seidel y el método Sucesivo sobre Relajación (o SOR). Ilustramos estos tres métodos mostrando cómo resolver la ecuación bidimensional de Poisson, una ecuación que luego necesitaremos resolver para determinar el campo de flujo más allá de un obstáculo

La ecuación de Poisson viene dada por

\[-\nabla^{2} \Phi=f, \nonumber \]

donde

\[\nabla^{2}=\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}} \nonumber \]

es el usual laplaciano bidimensional. Esto podría ser una ecuación lineal con\(f\) independiente de\(\Phi\), o una ecuación no lineal donde\(f\) puede ser alguna función no lineal de\(\Phi\).

Después de discretizar la ecuación de Poisson usando la aproximación de diferencia finita centrada para las segundas derivadas, obtenemos en una cuadrícula con espaciado de cuadrícula uniforme\(h\),

\[4 \Phi_{i, j}-\Phi_{i+1, j}-\Phi_{i-1, j}-\Phi_{i, j+1}-\Phi_{i, j-1}=h^{2} f_{i, j} . \nonumber \]

El método Jacobi simplemente resuelve la ecuación discretizada (7.1) para\(\Phi_{i, j}\) iterativamente. Con superíndices que indican pasos de iteración, tenemos

\[\Phi_{i, j}^{(n+1)}=\frac{1}{4}\left(\Phi_{i+1, j}^{(n)}+\Phi_{i-1, j}^{(n)}+\Phi_{i, j+1}^{(n)}+\Phi_{i, j-1}^{(n)}+h^{2} f_{i, j}^{(n)}\right) . \nonumber \]

En el antiguo lenguaje de programación científica FORTRAN-77, la implementación del método Jacobi requirió el guardado\(\Phi\) en dos matrices diferentes, una correspondiente a la iteración\(n\) -ésima y otra correspondiente a la iteración\((n+1)\) -st. Cuando la iteración se realizó con una sola matriz, el método se llamó Gauss-Seidel. En el método estándar de Gauss-Seidel, la matriz se actualizó fila por fila y tenía la forma

\[\Phi_{i, j}^{(n+1)}=\frac{1}{4}\left(\Phi_{i+1, j}^{(n)}+\Phi_{i-1, j}^{(n+1)}+\Phi_{i, j+1}^{(n)}+\Phi_{i, j-1}^{(n+1)}+h^{2} f_{i, j}^{(n)}\right) . \nonumber \]

El método Gauss-Seidel tuvo la doble ventaja de requerir menos memoria y converger más rápidamente que el método Jacobi.

Una variante de Gauss-Seidel que también se puede encontrar en los libros de texto se llama Gauss-Seidel rojo-negro. En este algoritmo, la cuadrícula se ve como un tablero de ajedrez con cuadrados rojos y negros. Se\(\Phi_{i, j}\) realiza una actualización de en dos pasadas: en la primera pasada,\(\Phi_{i, j}\) se actualiza sólo en las casillas rojas; en la segunda pasada, sólo en las casillas negras. Debido a la estructura del operador de diferencia finita laplaciana, al resolver\(\nabla^{2} \Phi=0\) los valores actualizados de\(\Phi\) en los cuadrados rojos dependen solo de los valores de\(\Phi\) en los cuadrados negros, y los valores actualizados en los cuadrados negros dependen solo del rojo cuadrados.

Traduciendo FORTRAN-77 directamente a MATLAB, el método Gauss-Seidel en la forma estándar podría implementarse en una cuadrícula uniforme con\(N-1\) puntos de cuadrícula\(M-1\) internos en las\(y\) direcciones\(x\) -y -respectivamente, como

Hoy en día, sin embargo, lenguajes de programación como MATLAB operan sobre vectores, que están optimizados para computadoras modernas, y los bucles explícitos que solían ser el caballo de batalla de FORTRAN77 ahora están vectorizados.

Entonces, para implementar correctamente el método Jacobi, digamos, en MATLAB, se pueden predefinir los vectores índice 1 e índice 2 que contienen los números de índice de los índices primero y segundo de la variable matricial phi. Estas definiciones serían

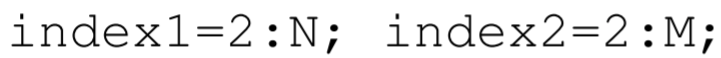
donde indexl e índice 2 hacen referencia a los puntos internos de la cuadrícula del dominio. Se supone que la variable phi se conoce en los límites del dominio correspondiente a los índices\((1,1)\),\((N+1,1),(1, M+1)\), y\((N+1, M+1)\). El método Jacobi en MATLAB se puede codificar en una línea como

El método rojo-negro Gauss-Seidel podría implementarse de una manera algo similar. Ahora hay que predefinir los vectores incluso 1, odd1, even 2 y odd2, con definiciones

El método Gauss-Seidel rojo-negro requiere entonces las siguientes cuatro líneas de codificación para implementar:

Cada iteración del método Gauss-Seidel rojo-negro se ejecutará más lentamente que la del método Jacobi, y el método rojo-negro Gauss-Seidel solo será útil si las iteraciones más lentas son compensadas por una convergencia más rápida. En la práctica, sin embargo, el método Jacobi o el método rojo-negro Gauss Seidel se sustituye por el método Sucesivo sobre Relajación (método SOR) correspondiente. Ilustraremos este método usando el método Jacobi, aunque el mejor enfoque es usar Gauss-Seidel rojo-negro.

El método Jacobi se reescribe primero sumando y restando el término diagonal\(\Phi_{i, j}^{(n)}\):

\[\Phi_{i, j}^{(n+1)}=\Phi_{i, j}^{(n)}+\frac{1}{4}\left(\Phi_{i+1, j}^{(n)}+\Phi_{i-1, j}^{(n)}+\Phi_{i, j+1}^{(n)}+\Phi_{i, j-1}^{(n)}-4 \Phi_{i, j}^{(n)}+h^{2} f_{i, j}^{(n)}\right) \nonumber \]

En esta forma, vemos que el método Jacobi actualiza el valor de\(\Phi_{i, j}\) en cada iteración. Podemos ampliar o disminuir esta actualización introduciendo un parámetro de relajación\(\lambda\). Tenemos

\[\Phi_{i, j}^{(n+1)}=\Phi_{i, j}^{(n)}+\frac{\lambda}{4}\left(\Phi_{i+1, j}^{(n)}+\Phi_{i-1, j}^{(n)}+\Phi_{i, j+1}^{(n)}+\Phi_{i, j-1}^{(n)}-4 \Phi_{i, j}^{(n)}+h^{2} f_{i, j}^{(n)}\right) \nonumber \]

que se puede escribir de manera más eficiente como

\[\Phi_{i, j}^{(n+1)}=(1-\lambda) \Phi_{i, j}^{(n)}+\frac{\lambda}{4}\left(\Phi_{i+1, j}^{(n)}+\Phi_{i-1, j}^{(n)}+\Phi_{i, j+1}^{(n)}+\Phi_{i, j-1}^{(n)}+h^{2} f_{i, j}^{(n)}\right) \nonumber \]

Cuando se usa con Gauss-Seidel, a menudo se\(1<\lambda<2\) puede usar un valor de\(\lambda\) en el rango para acelerar la convergencia de la iteración. Cuando\(\lambda>1\), el modificador sobre en Sucesivo Sobre Relajación es apto. Cuando el lado derecho de la ecuación de Poisson es una función no lineal de\(\Phi\), sin embargo, el método\(\lambda=1\) Gauss-Seidel puede no converger. En este caso, puede ser razonable elegir un valor\(\lambda\) menor a uno, y tal vez un nombre mejor para el método sería Sucesivo Bajo Relajación. Al estar bajo relajación, la convergencia de la iteración, por supuesto, se ralentizará. Pero este es el costo que a veces hay que pagar por la estabilidad.

Método de Newton para un sistema de ecuaciones no lineales

Un sistema de ecuaciones no lineales se puede resolver usando una versión del Método iterativo de Newton para encontrar raíces. Aunque en la práctica, el método de Newton a menudo se aplica a un gran sistema no lineal, aquí ilustraremos el método para el sistema simple de dos ecuaciones y dos incógnitas.

Supongamos que queremos resolver

\[f(x, y)=0, \quad g(x, y)=0, \nonumber \]

por las incógnitas\(x\) y\(y\). Queremos construir dos secuencias simultáneas\(x_{0}, x_{1}, x_{2}, \ldots\) y\(y_{0}, y_{1}, y_{2}, \ldots\) que converjan a las raíces. Para construir estas secuencias, las series Taylor expandimos\(f\left(x_{n+1}, y_{n+1}\right)\) y\(g\left(x_{n+1}, y_{n+1}\right)\) sobre el punto\(\left(x_{n}, y_{n}\right) .\) Usando las derivadas parciales\(f_{x}=\)\(\partial f / \partial x, f_{y}=\partial f / \partial y\), etc., las expansiones bidimensionales de la serie Taylor, mostrando solo las lineales términos, están dados por

\[\begin{array}{ll} f\left(x_{n+1}, y_{n+1}\right)=f\left(x_{n}, y_{n}\right)+\left(x_{n+1}-x_{n}\right) f_{x}\left(x_{n}, y_{n}\right) & +\left(y_{n+1}-y_{n}\right) f_{y}\left(x_{n}, y_{n}\right)+\ldots \\ g\left(x_{n+1}, y_{n+1}\right)=g\left(x_{n}, y_{n}\right)+\left(x_{n+1}-x_{n}\right) g_{x}\left(x_{n}, y_{n}\right) & +\left(y_{n+1}-y_{n}\right) g_{y}\left(x_{n}, y_{n}\right)+\ldots . \end{array} \nonumber \]

Para obtener el método de Newton\(f\left(x_{n+1}, y_{n+1}\right)=0, g\left(x_{n+1}, y_{n+1}\right)=0\), tomamos y soltamos términos de orden superior por encima de los lineales. Aunque entonces se puede encontrar un sistema de ecuaciones lineales para\(x_{n+1}\) y\(y_{n+1}\), es más conveniente definir las variables

\[\Delta x_{n}=x_{n+1}-x_{n}, \quad \Delta y_{n}=y_{n+1}-y_{n} \nonumber \]

Las ecuaciones de iteración serán dadas por

\[x_{n+1}=x_{n}+\Delta x_{n}, \quad y_{n+1}=y_{n}+\Delta y_{n} \nonumber \]

y las ecuaciones lineales a resolver\(\Delta x_{n}\) y\(\Delta y_{n}\) están dadas por

\[\left(\begin{array}{ll} f_{x} & f_{y} \\ g_{x} & g_{y} \end{array}\right)\left(\begin{array}{l} \Delta x_{n} \\ \Delta y_{n} \end{array}\right)=\left(\begin{array}{l} -f \\ -g \end{array}\right), \nonumber \]

donde\(f, g, f_{x}, f_{y}, g_{x}\), y\(g_{y}\) son todos evaluados en el punto\(\left(x_{n}, y_{n}\right) .\) El caso bidimensional se generaliza fácilmente a\(n\) las dimensiones. La matriz de derivadas parciales se llama Matriz Jacobiana.

Ilustramos el Método de Newton encontrando numéricamente la solución de estado estacionario de las ecuaciones de Lorenz, dada por

\[\begin{aligned} \sigma(y-x) &=0, \\ r x-y-x z &=0, \\ x y-b z &=0, \end{aligned} \nonumber \]

donde\(x, y\), y\(z\) son las variables desconocidas y\(\sigma, r\), y\(b\) son los parámetros conocidos. Aquí, tenemos un sistema homogéneo tridimensional\(f=0, g=0\), y\(h=0\), con

\[\begin{aligned} &f(x, y, z)=\sigma(y-x), \\ &g(x, y, z)=r x-y-x z, \\ &h(x, y, z)=x y-b z . \end{aligned} \nonumber \]

Las derivadas parciales se pueden calcular para ser

\[\begin{array}{lll} f_{x}=-\sigma, & f_{y}=\sigma, & f_{z}=0, \\ g_{x}=r-z, & g_{y}=-1, & g_{z}=-x, \\ h_{x}=y, & h_{y}=x, & h_{z}=-b . \end{array} \nonumber \]

Por lo tanto, la ecuación de iteración es

\[\left(\begin{array}{ccc} -\sigma & \sigma & 0 \\ r-z_{n} & -1 & -x_{n} \\ y_{n} & x_{n} & -b \end{array}\right)\left(\begin{array}{c} \Delta x_{n} \\ \Delta y_{n} \\ \Delta z_{n} \end{array}\right)=-\left(\begin{array}{c} \sigma\left(y_{n}-x_{n}\right) \\ r x_{n}-y_{n}-x_{n} z_{n} \\ x_{n} y_{n}-b z_{n} \end{array}\right) \nonumber \]

con

\[\begin{aligned} &x_{n+1}=x_{n}+\Delta x_{n}, \\ &y_{n+1}=y_{n}+\Delta y_{n}, \\ &z_{n+1}=z_{n}+\Delta z_{n} . \end{aligned} \nonumber \]

El programa MATLAB de muestra que resuelve este sistema está en el m-file newton_system.m.