1.9: PDE Lineal de Primer Orden

Solo consideramos la ODE hasta el momento, así que resolvamos una PDE lineal de primer orden. Considere la ecuación\[a(x,t) \, u_x + b(x,t) \, u_t + c(x,t) \, u = g(x,t), \qquad u(x,0) = f(x) , \qquad -\infty < x < \infty, \quad t > 0 , \nonumber \] donde\(u(x,t)\) es una función de\(x\) y\(t\). La condición inicial\(u(x,0) = f(x)\) es ahora una función de\(x\) más que solo un número. En estos problemas, es útil pensar en la\(x\) posición y\(t\) como el tiempo. La ecuación describe la evolución de una función de a\(x\) medida que pasa el tiempo. Abajo, los coeficientes\(a\),\(b\),\(c\), y la función en su mayoría\(g\) van a ser constantes o cero. El método que describimos funciona con coeficientes no constantes, aunque los cálculos pueden llegar a ser difíciles rápidamente.

Este método que utilizamos es el. La idea es que encontremos líneas a lo largo de las cuales la ecuación es una ODE que resolvemos. Volveremos a ver esta técnica para PDE de segundo orden cuando encontremos la ecuación de onda en la Sección 4.8.

Ejemplo\(\PageIndex{1}\)

Considerar la ecuación\[u_t + \alpha u_x = 0, \qquad u(x,0) = f(x) . \nonumber \] Esta ecuación particular,\(u_t + \alpha u_x = 0\), se llama la ecuación de transporte.

Los datos se propagarán a lo largo de curvas llamadas características. La idea es cambiar a las llamadas coordenadas características. Si cambiamos a estas coordenadas, la ecuación se simplifica. El cambio de variables para esta ecuación es

\[\xi = x - \alpha t , \qquad s = t . \nonumber \]

Veamos en qué se convierte la ecuación. Recuerda la regla de la cadena en varias variables.

\[\begin{align}\begin{aligned} & u_t = u_\xi \xi_t + u_s s_t = - \alpha u_\xi + u_s , \\ & u_x = u_\xi \xi_x + u_s s_x = u_\xi .\end{aligned}\end{align} \nonumber \]

La ecuación en las coordenadas\(\xi\) y\(s\) se convierte

\[\underbrace{(- \alpha u_\xi + u_s)}_{u_t} + \alpha \underbrace{(u_\xi)}_{u_x} = 0 , \nonumber \]

o en otras palabras\[u_s = 0 . \nonumber \]

Eso es trivial de resolver. Tratando simplemente\(\xi\) como un parámetro, hemos obtenido la ODE\(\frac{d u}{d s} = 0\).

La solución es una función de la que no depende\(s\) (pero sí depende de\(\xi\)). Es decir, hay alguna función\(A\) tal que\[u = A(\xi) = A(x - \alpha t) . \nonumber \] La condición inicial dice que:\[f(x) = u(x,0) = A(x - \alpha 0) = A(x) , \nonumber \] así\(A=f\). En otras palabras,\[u(x,t) = f(x-\alpha t) . \nonumber \] Todo simplemente se mueve a la derecha a la velocidad a\(\alpha\) medida que\(t\) aumenta. La curva dada por la ecuación\[\xi = \text{constant} \nonumber \]

se llama la característica. Ver Figura\(\PageIndex{1}\). En este caso, la solución no cambia a lo largo de la característica.

Figura\(\PageIndex{1}\): Curvas características.

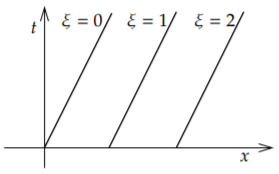
En las\((x,t)\) coordenadas, las curvas características satisfacen\(t = \frac{1}{\alpha} ( x- \xi)\), y de hecho son líneas. La pendiente de las líneas características es\(\frac{1}{\alpha}\), y para cada diferente\(\xi\) obtenemos una línea característica diferente.

Vemos por qué\(u_t + \alpha u_x = 0\) se llama la ecuación del transporte: todo viaja a cierta velocidad constante. A veces esto se llama. Un ejemplo de aplicación es el material que se mueve por un río donde el material no se difunde y simplemente se transporta. En esta configuración,\(x\) es la posición a lo largo del río,\(t\) es el tiempo, y\(u(x,t)\) la concentración el material en la posición\(x\) y el tiempo\(t\). Ver Figura\(\PageIndex{2}\) para un ejemplo.

Figura\(\PageIndex{2}\): Ejemplo de “transporte” en\(u_{t}-u_{x}=0\) (es decir,\(\alpha =1\)) donde la condición inicial\(f(x)\) es un pico en el origen. A la izquierda hay una gráfica de la condición inicial\(u(x,0)\). A la derecha hay una gráfica de la función\(u(x,1)\), es decir en el momento\(t=1\). Observe que es la misma gráfica desplazada una unidad a la derecha.

Usamos idea similar en el caso más general:\[a u_x + b u_t + c u = g, \qquad u(x,0) = f(x) . \nonumber \] Cambiamos las coordenadas a las coordenadas características. Llamemos a estas coordenadas\((\xi,s)\). Estas son coordenadas donde\(a u_x + b u_t\) se convierte en diferenciación en la\(s\) variable.

A lo largo de las curvas características (donde\(\xi\) es constante), obtenemos una nueva ODE en la\(s\) variable. En la ecuación de transporte, conseguimos lo simple\(\frac{du}{ds} = 0\). En general, obtenemos la ecuación lineal\[\label{eq:fopde:charode} \frac{du}{ds} + c u = g. \]

Pensamos en todo como una función de\(\xi\) y\(s\), aunque estamos pensando en un parámetro más que\(\xi\) como una variable independiente. Entonces la ecuación es una ODE. Se trata de una ODE lineal que podemos resolver utilizando el factor integrador.

Para encontrar las características, piense en una curva dada paramétricamente\(\bigl(x(s),t(s)\bigr)\). Tratamos de que la curva satisfaga\[\frac{dx}{ds} = a, \qquad \frac{dt}{ds} = b . \nonumber \] ¿Por qué? Porque cuando pensamos en\(x\) y\(t\) como funciones de\(s\) encontramos, usando la regla de la cadena,\[\frac{du}{ds} + c u = \underbrace{\left( u_x \frac{dx}{ds} + u_t \frac{dt}{ds}\right)}_{\frac{du}{ds}} + c u = a u_x + b u_t + c u = g . \nonumber \]

Entonces obtenemos la ODE\(\eqref{eq:fopde:charode}\), que luego describe el valor de la solución\(u\) de la PDE a lo largo de esta curva característica. También es conveniente asegurarse de que\(s=0\) corresponda a\(t=0\), es decir\(t(0) = 0\). Será conveniente también para\(x(0) = \xi\). Ver Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Curva característica general.

Ejemplo\(\PageIndex{2}\)

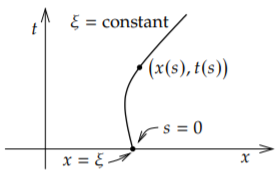
Considerar\[u_x + u_t + u = x, \qquad u(x,0) = e^{-x^2} . \nonumber \] Encontramos las características, es decir, las curvas dadas por So\[\frac{dx}{ds} = 1, \qquad \frac{dt}{ds} = 1 . \nonumber \]\[x = s + c_1, \qquad t = s+ c_2 , \nonumber \] para algunos\(c_1\) y\(c_2\). En\(s=0\) queremos\(t=0\), y\(x\) debemos ser\(\xi\). Así que dejamos\(c_1 = \xi\) y\(c_2 = 0\):\[x = s + \xi, \qquad t = s . \nonumber \]

La ODE es\(\frac{du}{ds} + u = x\), y\(x = s+\xi\). Entonces, la ODE a resolver a lo largo de\[\frac{du}{ds} + u = s+ \xi . \nonumber \] la característica es La solución general de esta ecuación, tratándola\(\xi\) como un parámetro, es\(u = C e^{-s}+s+\xi-1\), para alguna constante\(C\). Al\(s=0\), nuestra condición inicial es que\(u\) es\(e^{-\xi^2}\), ya que en\(s=0\) tenemos\(x=\xi\). Ante esta condición inicial, encontramos\(C=e^{-\xi^2} - \xi +1\). Entonces,

\[\begin{align}\begin{aligned} u & = \bigl(e^{-\xi^2} - \xi +1\bigr) e^{-s}+s+\xi-1 \\ & = e^{-\xi^2-s} + (1 - \xi) e^{-s} +s+\xi-1 . \end{aligned}\end{align} \nonumber \]

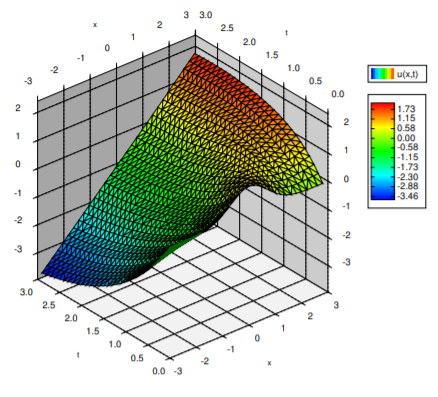
\(s=t\)Sustituir\(\xi = x-t\) y encontrar\(u\) en términos de\(x\) y\(t\):\[\begin{align}\begin{aligned} u & = e^{-\xi^2-s} + (1 - \xi) e^{-s} +s+\xi-1 \\ & = e^{-{(x-t)}^2-t} + (1 - x + t) e^{-t} +x-1 . \end{aligned}\end{align} \nonumber \] Ver Figura\(\PageIndex{4}\) para una gráfica de\(u(x,t)\) como una función de dos variables.

Figura\(\PageIndex{4}\): Gráfica de la solución\(u(x,t)\) a\(u_{x}+u_{t}+u=x\),\(u(x,0)=e^{-x^{2}}\).

Cuando los coeficientes no son constantes, las curvas características ya no van a ser líneas rectas.

Ejemplo\(\PageIndex{3}\)

Considere la siguiente ecuación de coeficiente variable:\[x u_x + u_t + 2 u = 0, \qquad u(x,0) = \cos(x) . % , \qquad -\infty < x < \infty, %\quad t > 0 . \nonumber \]

Encontramos las características, es decir, las curvas dadas por\[\frac{dx}{ds} = x, \qquad \frac{dt}{ds} = 1 . \nonumber \] So\[x = c_1 e^{s} , \qquad t = s+ c_2 . \nonumber \]

En\(s=0\), deseamos conseguir la línea\(t=0\), y\(x\) debería ser\(\xi\). Entonces\[x = \xi e^s, \qquad t = s . \nonumber \]

OK, la ODE que necesitamos resolver es\[\frac{du}{ds} + 2 u = 0 . \nonumber \]

Esto es para un fijo\(\xi\). Al\(s=0\), deberíamos conseguir que\(u\) sea\(\cos(\xi)\), así que esa es nuestra condición inicial. En consecuencia,\[u = e^{-2s} \cos(\xi)= e^{-2t} \cos(xe^{-t}) . \nonumber \]

Hacemos algunas observaciones finales. Una cosa a tener en cuenta es que nos meteríamos en problemas si el coeficiente delante de\(u_t\), es decir el\(b\), es siempre cero. Consideremos un ejemplo rápido de lo que puede salir mal:\[u_x + u = 0, \qquad u(x,0) = \sin(x). \nonumber \] Este problema no tiene solución. Si tuviéramos una solución, eso implicaría\(u_x(x,0) = \cos(x)\), pero\(u_x(x,0) + u(x,0) = \cos(x) + \sin(x) \not= 0\). El problema es que la curva característica es ahora la línea\(t=0\), ¡y la solución ya está provista en esa línea!

Siempre y cuando\(b\) sea distinto de cero, es conveniente asegurar que\(b\) sea positivo multiplicando por\(-1\) si es necesario, para que positivo\(s\) signifique positivo\(t\).

Otra observación es que si\(a\) o\(b\) en la ecuación son variables, los cálculos pueden salirse de control rápidamente, ya que las expresiones para las coordenadas características se vuelven desordenadas y luego resolver la ODE se vuelve aún más desordenada. En los ejemplos anteriores,\(b\) fue siempre\(1\), es decir, nos metimos\(s=t\) en las coordenadas características. Si no\(b\) es constante, tu expresión para\(s\) será más complicada.

Encontrar las coordenadas características es realmente un sistema de ODE en general si\(a\) depende\(t\) o si\(b\) depende de\(x\). En ese caso, necesitaríamos técnicas de sistemas de ODE para resolver, ver Capítulo 3 o Capítulo 8. En general, si\(a\) y no\(b\) son funciones lineales o constantes, puede ser imposible encontrar expresiones de forma cerrada para las coordenadas características.

Finalmente, el método de características se aplica también a la PDE no lineal de primer orden. En el caso no lineal, las características dependen no sólo de la ecuación diferencial, sino también de los datos iniciales. Esto lleva no sólo a cálculos más difíciles, sino también a la formación de singularidades donde la solución se descompone en un momento determinado. Una aplicación de ejemplo donde surgen PDE no lineales de primer orden es la teoría del flujo de tráfico, y probablemente hayas experimentado la formación de singularidades: los atascos. Pero nosotros digremos.