1.E: ODEs de primer orden (Ejercicios)
- Page ID
- 115492
Estos son ejercicios de tarea para acompañar el mapa de texto "Ecuaciones Diferenciales para Ingeniería" de Libl. Se trata de un libro de texto dirigido a un primer curso de un semestre sobre ecuaciones diferenciales, dirigido a estudiantes de ingeniería. El requisito previo para el curso es la secuencia básica de cálculo.
1.1: Integrales como soluciones
Resolver para\(v\), y luego resolver para\(x\). Encuentra\(x(10)\) para responder a la pregunta.
Resolver\(\dfrac{dy}{dx} = x^2 + x\) for \(y(1) = 3\).
Resolver\(\dfrac{dy}{dx} = \sin (5x)\) for \(y(0) = 2\).
Resolver\(\dfrac{dy}{dx} = \dfrac {1}{x^2 - 1}\) for \(y(0) = 0\).
Resolver\(y' = y^3\) for \(y(0) = 1\).
Resolver\(y' = \left({y-1}\right) \left({y + 1} \right)\) for \(y(0) = 3\).
Resolver\(\dfrac{dy}{dx} = \dfrac{1}{y+1}\) for \(y(0) = 0\).
Resolver\(y'' = \sin x\) for \(y(0) =0\), \(y'(0) = 2\).
Una nave espacial viaja a la velocidad\(2t^2 + 1\) km/s (\(t\)es tiempo en segundos). Está apuntando directamente lejos de la tierra y a la vez\(t = 0\) se encuentra a 1000 kilómetros de la tierra. ¿Qué tan lejos de la Tierra está a un minuto del tiempo\(t =0\)?
Resolver\(\dfrac{dx}{dt} = \sin (t^2) + t\), \(x(0) = 20\). Está bien dejar tu respuesta como una integral definitiva.
Una bola caída acelera hacia abajo a un ritmo constante\(9.8\) metros por segundo al cuadrado. Establecer la ecuación diferencial para la altura sobre el suelo\(h\) en metros. Entonces suponiendo\(h(0)=100\text{ meters}\), cuánto tiempo tarda la pelota en golpear el suelo.
Encuentra la solución general de\(y'=e^{x}\), y luego\(y'=e^{y}\).
Resolver\(\dfrac{dy}{dx} = e^x + x\) and \(y(0) = 10\).
- Contestar
-
\(y=e^{x}+\frac{x^{2}}{2}+9\)
Resolver\(x' = \dfrac{1}{x^2}\), \(x(1) = 1\).
- Contestar
-
\(x=(3t-2)^{1/3}\)
Resolver\(x'=\frac{1}{\cos (x)}\),\(x(0)=\frac{\pi}{2}\).
- Contestar
-
A\(x=\sin ^{-1}(t+1)\)
Sid está en un automóvil viajando a velocidad\(10t + 70\) millas por hora de distancia de Las Vegas, donde\(t\) está en horas. En\(t =0\) el Sid se encuentra a 10 millas de Las Vegas. ¿A qué distancia de Las Vegas está Sid\(2\) horas después?
- Contestar
-
\(170\)
Resolver\(y' = y''\), \(y(0) = 1\), donde\(n\) es un entero positivo. Pista: Hay que considerar diferentes casos.
- Contestar
-
Si\(n\neq 1\), entonces\(y=((1-n)x+1)^{1/(1-n)}\). Si\(n=1\), entonces\(y=e^{x}\).
La tasa de cambio del volumen de una bola de nieve que se está derritiendo es proporcional a la superficie de la bola de nieve. Supongamos que la bola de nieve es perfectamente esférica. El volumen (en centímetros cúbicos) de una bola de radio\(r\) centímetros es\(\frac{4}{3})\pi r^{3}\). La superficie es\(4\pi r^{2}\). Configura la ecuación diferencial de cómo\(r\) está cambiando el radio. Entonces, supongamos que en el tiempo\(t=0\) minutos, el radio es\(10\) centímetros. Después de\(5\) minutos, el radio es de\(8\) centímetros. ¿A qué hora\(t\) se derretirá completamente la bola de nieve?
- Contestar
-
La ecuación es\(r'=-C\) para alguna constante\(C\). La bola de nieve se fundirá completamente en\(25\) minutos a partir del tiempo\(t=0\).
Encuentre la solución general para\(y''''=0\). ¿Cuántas constantes distintas necesitas?
- Contestar
-
\(y=Ax^{3}+Bx^{2}+Cx+D\), por lo que\(4\) constantes.
1.2: Campos de taludes
Campo de pendiente de boceto para\(y' = e^{x-y}\). ¿Cómo se comportan las soluciones a medida\(x\) que crecen? ¿Puedes adivinar una solución particular mirando el campo de pendiente?
Campo de pendiente de boceto para\(y' = x^2\).
Campo de pendiente de boceto para\(y' = y^2\).
¿Es posible resolver la ecuación\(y' = \frac {xy}{\cos {x}} \) para\(y (0) = 1\)? Justificar.
¿Es posible resolver la ecuación\( y' = y \sqrt {\left \vert x \right \vert}\) para\( y(0) = 0 \)? ¿La solución es única? Justificar.
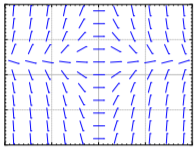
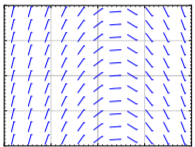
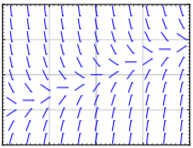
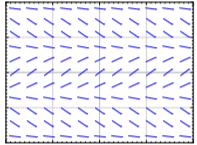
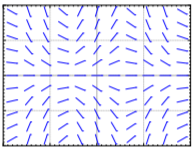
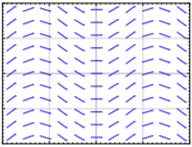
Hacer coincidir ecuaciones\(y' = 1 - x\), \(y' = x - 2y\), \( y' = x(1 - y) \) con campos de pendiente. Justificar.
Take \(y' = f(x, y)\), \( y(0) = 0\), where \( f(x, y) > 1 \) for all \(x\) and \(y\). If the solution exists for all \(x\), can you say what happens to \(y(x)\) as \(x\) goes to positive infinity? Explain.
Take \( (y - x)y' = 0\), \( x(0) = 0 \).
- Find two distinct solutions.
- Explain why this does not violate Picard’s theorem.
Suppose \(y'=f(x,y)\). What will the slope field look like, explain and sketch an example, if you know the following about \(f(x,y)\):
- \(f\) does not depend on \(y\).
- \(f\) does not depend on \(x\).
- \(f,(t,t)=0\) for any number \(t\).
- \(f(x,0)=0\) and \(f(x,1)=1\) for all \(x\).
Find a solution to \(y'=|y|\), \(y(0)=0\). Does Picard’s theorem apply?
Take an equation \(y'=(y-2x)g(x,y)+2\) for some function \(g(x,y)\). Can you solve the problem for the initial condition \(y(0)=0\), and if so what is the solution?
Suppose \(y'=f(x,y)\) is such that \(f(x,1)=0\) for every \(x,f\) is continuous and \(\frac{\partial f}{\partial y}\) exists and is continuous for every \(x\) and \(y\).
- Guess a solution given the initial condition \(y(0)=1\).
- Can graphs of two solutions of the equation for different initial conditions ever intersect?
- Given \(y(0)=0\), what can you say about the solution. In particular, can \(y(x)>1\) for any \(x\)? Can \(y(x)=1\) for any \(x\)? Why or why not?
Sketch the slope field of \( y' = y^3 \). Can you visually find the solution that satisfies \( y(0) = 0\)?
- Answer
-
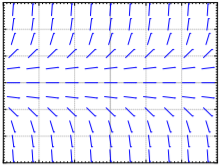
\(y=0\) is a solution such that \(y(0)=0\)
Is it possible to solve \( y' = xy \) for \( y(0) = 0 \)? Is the solution unique?
- Answer
-
Yes a solution exists. The equation is \(y'=f(x,y)\) where \(f(x,y)=xy\). The function \(f(x,y)\) is continuous and \(\frac{\partial f}{\partial y}=x\), which is also continuous near \((0, 0)\). So a solution exists and is unique. (In fact, \(y=0\) is the solution.)
Is it possible to solve \( y' = \frac {x}{x^2 - 1}\) for \( y(1) = 0 \)?
- Answer
-
No, the equation is not defined at \((x,y) = (1, 0)\).
Match equations \( y' = \sin x\), \(y' = \cos y\), \(y' = y \cos (x)\) to slope fields. Justify.
- Contestar
-
- \(y'=\cos y\)
- \(y'=y\cos (x)\)
- \(y'=\sin x\)
Justificación dejada al lector.
Supongamos
\[f(y)=\left\{\begin{array}{cc}{0}&{if\: y>0,} \\ {1}&{if\: y\leq 0.}\end{array}\right.\nonumber\]
¿\(y(0)=0\)Tiene\(y'=f(y)\), una solución continuamente diferenciable? ¿Aplica Picard? ¿Por qué, o por qué no?
- Contestar
-
Picard no aplica ya que no\(f\) es continuo en\(y=0\). La ecuación no tiene una solución continuamente diferenciable. Supongamos que sí. Observe eso\(y'(0)=1\). Por la primera prueba derivada,\(y(x)>0\) para pequeños positivos\(x\). Pero entonces para los que\(x\) tendríamos\(y'(x)=0\), así que claramente el derivado no puede ser continuo.
Considera una ecuación de la forma\(y'=f(x)\) para alguna función continua\(f\), y una condición inicial\(y(x_{0})=y_{0}\). ¿Existe una solución para todos\(x\)? ¿Por qué o por qué no?
- Contestar
-
La solución es\(y(x)=\int_{x_{0}}^{x}f(s)ds+y_{0}\), y esto sí existe para todos\(x\).
1.3: Ecuaciones separables
Resolver\(y' = \frac {x}{y}\).
Resolver\(y' = x^2y\).
Resolver\( \frac{dx}{dt} = \left ( x^2 -1 \right ) \), for \( x(0) = 0\).
Resolver\( \frac{dx}{dt} = x \sin (t)\), para\(x(0) = 1\).
Resolver\( \frac {dy}{dx} = xy + x + y + 1 \). Pista: Facturar el lado derecho.
Resolver\( xy' = y + 2x^2y\), donde\(y(1) = 1\).
Resolver\( \frac {dy}{dx} = \frac {y^2 + 1}{x^2 + 1} \), para\(y (0) = 1\).
Encuentra una solución implícita para\( \frac {dy}{dx} = \frac {x^2 + 1}{y^2 + 1} \), para\(y (0) = 1\).
Encuentre una solución explícita para\( y' = xe^{-y}\), \(y(0) = 1\).
Encuentre una solución explícita para\( xy' = e^{-y}\), para\(y(1) = 1\).
Encuentre una solución explícita para\( y' = ye^{-x^2}\), \(y(0) = 1\). Está bien dejar una integral definitiva en tu respuesta.
Supongamos que una taza de café está a 100 grados Celsius a la vez\(t =0\), está a 70 grados a los\(t = 10\) minutos, y está a 50 grados a los\(t = 20\) minutos. Compute la temperatura ambiente.
Resolver\( y' = 2xy\).
- Contestar
-
\(y=Ce^{x^{2}}\)
Resolver\( x' = 3xt^2 - 3t^2\), \( x(0) = 2 \).
- Contestar
-
\(y=e^{t^{3}}+1\)
Encuentre una solución implícita para\(x' = \frac {1}{3x^2 + 1}\) \( x(0) = 1\).
- Contestar
-
\(x^{3}+x=t+2\)
Encuentre una solución explícita para\( xy' = y^2\), \(y(1) = 1\).
- Contestar
-
\(y=\frac{1}{1-\ln x}\)
Encuentra una solución implícita para\(y' = \frac {\sin (x)}{ \cos (y)}\).
- Contestar
-
\(\sin (y)=-\cos (x)+C\)
T ake Ejemplo 1.3.3 con los mismos números:\(89\) degrees at \( t =0\), \(85\) degrees a\(t =1\), y temperatura ambiente de\(22\) degrees. Suppose these temperatures were measured with precisión de\( \pm 0.5\) grados. Dada esta imprecisión, el tiempo que tarda el café en enfriarse a (exactamente) 60 grados también solo se conoce en un cierto rango. Encuentra esta gama. Pista: Piense en qué tipo de error hace que el tiempo de enfriamiento sea más largo y qué más corto.
- Contestar
-
El rango es de aproximadamente\(7.45\) a\(12.15\) minutos.
Se\(x\) modela una población de conejos en una isla\(x'=x-(\frac{1}{1000})x^{2}\), donde la variable independiente es el tiempo en meses. En su momento\(t=0\), hay\(40\) conejos en la isla.
- Encuentra la solución a la ecuación con la condición inicial.
- Cuántos conejos hay en la isla en\(1\) mes,\(5\) meses,\(10\) meses,\(15\) meses (redondos al entero más cercano)
- Contestar
-
- \(x=\frac{1000e^{t}}{e^{t}+24}\).
- \(102\)conejos después de un mes,\(861\) después de\(5\) meses,\(999\) después de\(10\) meses,\(1000\) después de\(15\) meses.
1.4: Ecuaciones lineales y el factor integrador
En los ejercicios, siéntase libre de dejar la respuesta como una integral definitiva si no se puede encontrar una solución de forma cerrada. Si puede encontrar una solución de forma cerrada, debe darle eso.
Resolver\( y' + xy = x\).
Resolver\( y' + 6y = e^x\).
Resuelve\(y' +3x^2y = \sin(x)\,e^{-x^3}\) con\( y(0)=1\).
Resolver\(y' + \cos(x)\,y =\cos(x) \).
Resuelve\( \frac{1}{x^2+1}y'+xy = 3\) con\( y(0)=0\).
Supongamos que hay dos lagos ubicados en un arroyo. El agua limpia fluye hacia el primer lago, luego el agua del primer lago desemboca en el segundo lago, y luego el agua del segundo lago fluye más aguas abajo. El flujo de entrada y salida de cada lago es\(500\) liters per hour. The first lago contiene\(100\) thousand liters of water and the second lake contains \(200\) thousand liters of agua. Un camión con\(500\) kg of toxic substance crashes into the first lake. Assume that the water is estar continuamente mezclado perfectamente por el arroyo.
- Encontrar la concentración de sustancia tóxica en función del tiempo en ambos lagos.
- ¿Cuándo la concentración en el primer lago será inferior\(0.001\text{ kg}\) por litro?
- ¿Cuándo será máxima la concentración en el segundo lago?
La ley de enfriamiento de Newton establece que\(\frac{dx}{dt} = -k(x-A)\) dónde\(x\) está la temperatura,\(t\) es el tiempo,\(A\) es la temperatura ambiente, y\(k>0\) es una constante. Supongamos que\(A=A_0 \cos(\omega t)\) para algunas constantes\(A_0\) y\(\omega\). Es decir, la temperatura ambiente oscila (por ejemplo temperaturas nocturnas y diurnas).
- Encuentra la solución general.
- A largo plazo, ¿las condiciones iniciales marcarán mucha diferencia? ¿Por qué o por qué no?
Inicialmente la\(5\) grams of salt are dissolved in \(20\) liters of water. Brine with concentración de sal\(2\) grams of salt per liter is added at a rate of \(3\) liters a minute. The tank is se mezcla bien y se drena en\(3\) liters a minute. How long does the process have to continue until hay\(20\) grams of salt in the tank?
Inicialmente un tanque contiene\(10\) liters of pure water. Brine of unknown (but constant) concentración de sal está fluyendo en\(1\) liter per minute. The water is mixed well and drained at \(1\) litro por minuto. ¿En\(20\) minutes there are \(15\) grams of salt in the tank. What is the concentration of sal en la salmuera entrante?
Resolver\(y' + 3x^2y + x^2\).
- Contestar
-
\(y=Ce^{-x^{3}}+\frac{1}{3}\)
Resolver\(y' + 2\sin(2x)y=2\sin(2x)\) with \(y(\pi/2)=3\).
- Contestar
-
\(y=2e^{\cos (2x)+1}+1\)
Supongamos que se está bombeando un tanque de agua en\(3\:\frac{\text{L}}{\text{min}}\). El tanque de agua comienza a las\(10\text{ L}\) of clean water. Water with toxic substance is flowing into the tank at \(2\:\frac{\text{L}}{\text{min}}\), con concentración\(20t\:\frac{\text{g}}{\text{L}}\) en el momento\(t\). Cuando el tanque está medio vacío, ¿cuántos gramos de sustancia tóxica hay en el tanque (suponiendo una mezcla perfecta)?
- Contestar
-
\(250\)gramos
Supongamos que tenemos bacterias en un plato y supongamos que poco a poco estamos agregando una sustancia tóxica de tal manera que la tasa de crecimiento se esté desacelerando. Es decir, supongamos que\(\frac{dP}{dt}=(2-0.1\, t)P\). Si\(P(0)=1000\), encuentra la población en\(t=5\).
- Contestar
-
\(P(5)=1000e^{2\times 5-0.05\times 5^{2}}=1000e^{8.75}\approx 6.31\times 10^{6}\)
Un tanque de agua cilíndrico tiene agua que fluye a metros\(I\) cúbicos por segundo. Dejar\(A\) ser el área de la sección transversal del tanque en metros. Supongamos que el agua fluye desde el fondo del tanque a una tasa proporcional a la altura del nivel del agua. Configura la ecuación diferencial para\(h\), la altura del agua, introduciendo y nombrando las constantes que necesites. También debes dar las unidades para tus constantes.
- Contestar
-
\(Ah'=I-kh\), donde\(k\) es una constante con unidades\(\frac{\text{m}^{2}}{\text{s}}\).
1.5: Sustitución
Pista: No es necesario que las respuestas estén siempre en forma cerrada.
Resolver\( y' + y(x^2 - 1) + xy^6 = 0 \), con\( y(1) = 1\).
Resolver\( 2yy' + 1 = y^2 + x \), con\( y(0) = 1 \).
Resolver\( y' + xy = y^4 \), con\( y(0) = 1 \).
Resolver\( yy' + x = \sqrt {x^2 + y^2} \).
Resolver\( y' = {(x +y -1)}^2 \).
Resolver\( y' = \dfrac {x^2 - y^2}{xy} \), con\( y(1) = 2 \).
Resolver\(xy' + y + y^2 = 0\), \(y(1) = 2\).
- Contestar
-
\(y=\frac{2}{3x-2}\)
Resolver\( xy' + y + x = 0 \), \(y(1) = 1\).
- Contestar
-
\(y=\frac{3-x^{2}}{2x}\)
Resolver\( y^2y' = y^3 - 3x\), \(y(0) = 2\).
- Contestar
-
\(y=\left(7e^{3x}+3x+1\right)^{1/3}\)
S olve\( 2yy' = e^{y^2 - x^2} + 2x \).
- Contestar
-
\(y=\sqrt{x^{2}-\ln (C-x)}\)
1.6: Ecuaciones autónomas
Considerar\(x' = x^2\).
- Dibuja el diagrama de fases, encuentra los puntos críticos y márcalos estables o inestables.
- Esbozar soluciones típicas de la ecuación.
- Encuentre\(\lim \limits_{t\to\infty} x(t)\) para la solución con la condición inicial\(x(0) = -1\).
Vamos\(x' = \sin x\).
- Dibuja el diagrama de fases para\(-4\pi \leq x \leq 4\pi \). En este intervalo marcar los puntos críticos estables o inestables.
- Esbozar soluciones típicas de la ecuación.
- Encuentre\(\lim \limits_{t\to\infty} x(t)\) para la solución con la condición inicial\(x(0) = 1\).
Supongamos que\(f(x)\) es positivo para\(0 < x < 1\), es cero cuando\(x=0\) y\(x=1\), y es negativo para todos los demás\(x\).
- Dibuja el diagrama de fases para\(x' = f(x)\), encuentra los puntos críticos y márcalos estables o inestables.
- Esbozar soluciones típicas de la ecuación.
- Encuentre\(\lim \limits_{t\to\infty} x(t)\) para la solución con la condición inicial\(x(0) = 0.5\).
Comience con la ecuación logística\(\frac{dx}{dt} = kx (M -x)\). Supongamos que modificamos nuestra cosecha. Es decir, sólo cosecharemos una cantidad proporcional a la población actual. En otras palabras cosechamos\(hx\) por unidad de tiempo para algunos\(h > 0\) (Similar al ejemplo anterior con\(h\) reemplazado por\(hx\)).
- Construir la ecuación diferencial.
- Demostrar que si\(kM > h\), entonces la ecuación sigue siendo logística.
- ¿Qué pasa cuando\(kM < h\)?
Una enfermedad se está propagando por el país. \(x\)Sea el número de personas infectadas. Que la constante\(S\) sea el número de personas susceptibles a la infección. La tasa de infección\(\frac{dx}{dt}\) es proporcional al producto de personas ya infectadas,\(x\), y al número de personas susceptibles pero no infectadas,\(S-x\).
- Anote la ecuación diferencial.
- Supongamos\(x(0) > 0\), es decir, algunas personas se infectan a la vez\(t=0\), qué es\(\displaystyle \lim_{t\to\infty} x(t)\).
- ¿La solución a la parte b) concuerda con tu intuición? ¿Por qué o por qué no?
Vamos\(x' = (x-1)(x-2)x^2\).
- Dibuje el diagrama de fases y encuentre puntos críticos.
- Clasificar los puntos críticos.
- Si\(x(0) = 0.5\) entonces encuentra\(\lim \limits_{t\to\infty} x(t)\).
- Contestar
-
- \(0,\: 1,\: 2\)son puntos críticos.
- \(x=0\)es inestable (semistable),\(x=1\) estable y\(x=2\) inestable.
- \(1\)
Vamos\(x' = e^{-x}\).
- Encuentra y clasifica todos los puntos críticos.
- Encontrar\(\lim \limits_{t\to\infty} x(t)\) dado cualquier condición inicial.
- Contestar
-
- No hay puntos críticos.
- \(\infty\)
Supongamos que una población de peces en un lago satisface\(\frac{dx}{dt} = kx (M -x)\). Ahora supongamos que los peces se agregan continuamente en\(A\) peces por unidad de tiempo.
- Encuentra la ecuación diferencial para\(x\).
- ¿Cuál es la nueva población limitante?
- Contestar
-
- \(\frac{dx}{dt}=kx(M-x)+A\)
- \(\frac{kM+\sqrt{(kM)^{2}+4Ak}}{2k}\)
Supongamos\(\frac{dx}{dt} = (x-\alpha)(x-\beta)\) para dos números\(\alpha < \beta\).
- Encuentre los puntos críticos y clasifíquelos.
Para b), c), d), encontrar con\(\displaystyle \lim_{t\to\infty} x(t)\) base en el diagrama de fases.
- \(x(0) < \alpha\),
- \(\alpha < x(0) < \beta\),
- \(\beta < x(0)\).
- Contestar
-
- \(\alpha\)es un punto crítico estable,\(\beta\) es inestable.
- \(\alpha\)
- \(\alpha\)
- \(\infty\)o DNE.
1.7: Métodos numéricos: método de Euler
Considerar\(\frac{dx}{dt} = (2t - x)^2\), \(x(0) = 2\). Utilice el método de Euler con tamaño de paso\(h = 0.5\) para aproximarse\(x(1)\).
Considerar\(\frac{dx}{dt} = t -x \), \(x(0) = 1\).
- Utilice el método de Euler con tamaños de paso\(h = 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}\) para aproximarse\(x(1)\).
- Resuelve la ecuación exactamente.
- Describe lo que sucede con los errores de cada uno\(h\) que usaste. Es decir, encuentra el factor por el cual el error cambió cada vez que redujo a la mitad el intervalo.
Aproximar el valor\(e\) de mirando el problema de valor inicial\(y' = y\) con\(y(0) = 1\) y aproximando\(y(1)\) usando el método de Euler con un tamaño de paso de\(0.2\).
Ejemplo de inestabilidad numérica: Tomar\(y' = -5y\), \(y(0) = 1\). Sabemos que la solución debe decaer a cero a medida que\(x\) crece. Usando el método de Euler, comienza con\(h =1\) y calcula\(y_1, y_2, y_3, y_4\) para intentar aproximar\(y(4)\). ¿Qué pasó? Ahora reducir a la mitad el intervalo. Sigue recortando a la mitad el intervalo y aproximando\(y(4)\) hasta que los números que estás obteniendo comiencen a estabilizarse (es decir, hasta que empiecen a ir hacia cero). Nota: Es posible que desee usar una calculadora.
El método más simple utilizado en la práctica es el método Runge-Kutta. Considere\(\frac{dy}{dx} = f(x, y)\),\(y(x_0) = y_0\) y un tamaño de paso\(h\). Todo es igual que en el método de Euler, excepto el cómputo de\(y_{i+1}\) y\(x_{i+1}\).
\[\begin{align}\begin{aligned} k_1 &= f(x_i, y_i), \\ k_2 &= f(x_i + \frac{h}{2}, y_i +k_1 \frac{h}{2}) & x_{i+1} = x_i + h, \\ k_3 &= f(x_i + \frac{h}{2}, y_i +k_2 \frac{h}{2}) & y_{i+1} = y_i + \dfrac{k_1 + 2k_2 + 2k_3 + k_4}{6}h, \\ k_4 &= f(x_i + h, y_i +k_3h).\end{aligned}\end{align}\]
Considerar\(\frac{dy}{dx} = yx^2\), \(y(0) = 1\).
- Use Runge-Kutta (ver arriba) con tamaños de escalón\(h = 1\) y\(h = \frac{1}{2}\) para aproximarse\(y(1)\).
- Utilice el método de Euler con\(h = 1\) y\(h = \frac{1}{2}\).
- Resuelve exactamente, encuentra el valor exacto de\(y(1)\), y compara.
Vamos\(x' = \sin (xt)\), y\(x(0) = 1\). Aproximado\(x(1)\) usando el método de Euler con tamaños de paso\(1\), \(0.5\), \(0.25\). Use a calculator and compute up to \(4\) decimal digits.
- Contestar
-
Aproximadamente:\(1.0000,\: 1.2397,\: 1.382\)
Vamos\(x' = 2t\), y\(x(0) = 0\).
- Aproximado\(x(4)\) usando el método de Euler con tamaños de paso\(4\), \(2\), and \(1\).
- Resuelve exactamente y calcula los errores.
- Calcular el factor por el cual cambiaron los errores.
- Contestar
-
- \(0,\: 8,\: 12\)
- \(x(4) = 16,\)por lo que los errores son:\(16,\: 8,\: 4\).
- Los factores son\(0.5,\: 0.5,\: 0.5\).
Vamos\(x' = xe^{xt+1}\), y\(x(0) = 0\).
- Aproximado\(x(4)\) usando el método de Euler con tamaños de paso\(4\), \(2\), and \(1\).
- Adivina una solución exacta basada en la parte a) y calcula los errores.
- Contestar
-
- \(0,\: 0,\: 0\)
- \(x=0\)es una solución por lo que los errores son:\(0,\: 0,\: 0\).
Hay una manera sencilla de mejorar el método de Euler para convertirlo en un método de segundo orden haciendo solo un paso adicional. Considere\(\frac{dy}{dx}=f(x,y)\),\(y(x_0) = y_0\), y un tamaño de paso\(h\). Lo que hacemos es pretender que calculamos el siguiente paso como en Euler, es decir, empezamos con\((x_i,y_i)\), calculamos una pendiente\(k_1 = f(x_i,y_i)\), y luego miramos el punto\((x_i+h,y_i + k_1h)\). En lugar de dejar que nuestro nuevo punto sea\((x_i+h,y_i + k_1h)\), calculamos la pendiente en ese punto\(k_2\), lo llamamos, y luego tomamos el promedio de\(k_1\) y\(k_2\), esperando que el promedio esté más cerca de la pendiente real en el intervalo de \(x_i\)a\(x_i+h\). Y estamos en lo cierto, si redujimos a la mitad el paso, el error debería bajar por un factor de\(2^2 = 4\). Para resumir, la configuración es la misma que para Euler regular, excepto el cálculo de\(y_{i+1}\) y\(x_{i+1}\).
\[\begin{align}\begin{aligned} & k_1 = f(x_i,y_i) , & & x_{i+1} = x_i + h , \\ & k_2 = f(x_i + h,y_i + k_1h) , & & y_{i+1} = y_i + \frac{k_1+k_2}{2}\,h .\end{aligned}\end{align}\]
Considerar\(\dfrac{dy}{dx} = x+y\),\(y(0)=1\).
- Utilice el método mejorado de Euler (ver arriba) con tamaños de paso\(h=\frac{1}{4}\) y\(h=\frac{1}{8}\) para aproximarse\(y(1)\).
- Utilice el método de Euler con\(h=\frac{1}{4}\) y\(h=\frac{1}{8}\).
- Resuelve exactamente, encuentra el valor exacto de\(y(1)\).
- Calcular los errores, y los factores por los cuales los errores cambiaron.
- Contestar
-
- Euler mejorado:\(y(1)\approx 3.3897\) para\(h=1/4\),\(y(1)\approx 3.4237\) para\(h=1/8\),
- Standard Euler:\(y(1)\approx 2.8828\) para\(h=1/4\),\(y(1)\approx 3.1316\) para\(h=1/8\),
- \(y=2e^{x}-x-1\), así\(y(2)\) es aproximadamente\(3.4366\).
- Errores aproximados para Euler mejorado:\(0.046852\) para\(h=1/4\) y\(0.012881\) para\(h=1/8\). Para Euler estándar:\(0.55375\) para\(h=1/4\), y\(0.30499\) para\(h=1/8\). El factor es aproximadamente\(0.27\) para Euler mejorado y\(0.55\) para Euler estándar.
1.8 Ecuaciones Exactas
Resuelve las siguientes ecuaciones exactas, bastarán las soluciones generales implícitas:
- \((2 xy + x^2) \, dx + (x^2+y^2+1) \, dy = 0\)
- \(x^5 + y^5 \frac{dy}{dx} = 0\)
- \(e^x+y^3 + 3xy^2 \frac{dy}{dx} = 0\)
- \((x+y)\cos(x)+\sin(x) + \sin(x)y' = 0\)
Encuentre el factor de integración para las siguientes ecuaciones convirtiéndolas en ecuaciones exactas:
- \(e^{xy} \, dx + \frac{y}{x} e^{xy} \, dy = 0\)
- \(\frac{e^x+y^3}{y^2} \, dx + 3x \, dy = 0\)
- \(4(y^2+x) \, dx + \frac{2x+2y^2}{y} \, dy = 0\)
- \(2\sin(y) \, dx + x\cos(y)\, dy = 0\)
Supongamos que tiene una ecuación de la forma:\(f(x) + g(y) \frac{dy}{dx} = 0\).
- Demostrar que es exacto.
- Encontrar la forma de la función potencial en términos de\(f\) y\(g\).
Supongamos que tenemos la ecuación\(f(x) \, dx - dy = 0\).
- ¿Es exacta esta ecuación?
- Encuentra la solución general usando una integral definida.
Encuentra la función potencial\(F(x,y)\) de la ecuación exacta\(\frac{1+xy}{x}\, dx + \bigl(\frac{1}{y} + x \bigr) \, dy = 0\) de dos maneras diferentes.
- Integrar\(M\) en términos de\(x\) y luego diferenciar\(y\) y establecer en\(N\).
- Integrar\(N\) en términos de\(y\) y luego diferenciar\(x\) y establecer en\(M\).
Se dice que una función\(u(x,y)\) es un if\(u_{xx} + u_{yy} = 0\).
- Mostrar si\(u\) es armónico,\(-u_y \, dx + u_x \, dy = 0\) es una ecuación exacta. Entonces existe (al menos localmente) la llamada función\(v(x,y)\) tal que\(v_x = -u_y\) y\(v_y = u_x\).
Verifique que los siguientes\(u\) sean armónicos y encuentre los conjugados armónicos correspondientes\(v\):
- \(u = 2xy\)
- \(u = e^x \cos y\)
- \(u = x^3-3xy^2\)
Resuelve las siguientes ecuaciones exactas, bastarán las soluciones generales implícitas:
- \(\cos(x)+ye^{xy} + xe^{xy} y' = 0\)
- \((2x+y)\, dx + (x-4y) \, dy = 0\)
- \(e^x + e^y \frac{dy}{dx} = 0\)
- \((3x^2+3y)\,dx + (3y^2+3x)\, dy = 0\)
- Contestar
-
- \(e^{xy}+\sin (x)=C\)
- \(x^{2}+xy-2y^{2}=C\)
- \(e^{x}+e^{y}=C\)
- \(x^{3}+3xy+y^{3}=C\)
Encuentre el factor de integración para las siguientes ecuaciones convirtiéndolas en ecuaciones exactas:
- \(\frac{1}{y}\, dx + 3y \, dy = 0\)
- \(dx - e^{-x-y} \, dy = 0\)
- \(\bigl( \frac{\cos(x)}{y^2} + \frac{1}{y} \bigr) \, dx + \frac{x}{y^2} \, dy = 0\)
- \(\bigl( 2y + \frac{y^2}{x} \bigr) \, dx + ( 2y+x )\, dy = 0\)
- Responder
-
- El factor integrador es\(y\), la ecuación se convierte\(dx+3y^{2}dy=0\).
- El factor integrador es\(e^{x}\), la ecuación se convierte\(e^{x}dx-e^{-y}dy=0\).
- El factor integrador es\(y^{2}\), la ecuación se convierte\((\cos(x)+y)dx+xdy=0\).
- El factor integrador es\(x\), la ecuación se convierte\((2xy+y^{2})dx+(x^{2}+2xy)dy=0\).
- Demostrar que cada ecuación separable\(y' = f(x)g(y)\) puede escribirse como una ecuación exacta, y verificar que efectivamente sea exacta.
- Usando esta reescritura\(y' = xy\) como una ecuación exacta, resuelva y verifique que la solución sea la misma que estaba en el Ejemplo 1.3.1.
- Responder
-
- La ecuación es\(-f(x)dx+\frac{1}{g(y)}dy\), y esto es exacto porque\(M=-f(x)\),\(N=\frac{1}{g(y)}\), entonces\(M_{y}=0=N_{x}\).
- \(-xdx+\frac{1}{y}dy=0\), lleva a la función potencial\(F(x,y)=-\frac{x^{2}}{2}+\ln|y|\), la resolución\(F(x,y)=C\) conduce a la misma solución que el ejemplo.
1.9: PDE Lineal de Primer Orden
Resolver
- \(u_t +9u_x = 0\),\(u(x,0) = \sin(x)\),
- \(u_t -8u_x = 0\),\(u(x,0) = \sin(x)\),
- \(u_t +\pi u_x = 0\),\(u(x,0) = \sin(x)\),
- \(u_t + \pi u_x + u = 0\),\(u(x,0) = \sin(x)\).
Resolver\(u_t +3u_x = 1\),\(u(x,0) = x^2\).
Resolver\(u_t +3u_x = x\),\(u(x,0) = e^x\).
Resolver\(u_x+u_t+xu = 0\),\(u(x,0) = \cos(x)\).
- Encuentra las coordenadas características para las siguientes ecuaciones:
\(u_x+u_t + u = 1\),\(u(x,0) = \cos(x)\),)\(2u_x+2u_t +2u = 2\),\(u(x,0) = \cos(x)\). - Resuelve las dos ecuaciones usando las coordenadas.
- Explica por qué obtuviste la misma solución, aunque las coordenadas características que encontraste eran diferentes.
Resolver\((1+x^2) u_t + x^2 u_x + e^x u = 0\),\(u(x,0) = 0\). Pista: Piensa un poco fuera de la caja.
Resolver
- \(u_t - 5u_x = 0\),\(u(x,0) = \frac{1}{1+x^2}\),
- \(u_t + 2u_x = 0\),\(u(x,0) = \cos(x)\).
- Responder
-
- \(u=\frac{1}{1+(x+5t)^{2}}\)
- \(u=\cos (x-2t)\)
Resolver\(u_x+u_t+tu = 0\),\(u(x,0) = \cos(x)\).
- Responder
-
\(u=\cos (x-t)e^{-t^{2}/2}\)
Resolver\(u_x+u_t = 5\),\(u(x,0) = x\).
- Responder
-
\(u=x+4t\)