20.9: Área en los planos y esferas neutrales

Última actualización
Guardar como PDF

Page ID: 114517

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El área se puede definir en los planos neutros y esferas. En la definición, el cuadrado unitario sólido$\mathcal{K}_1$ tiene que ser intercambiado por un conjunto poligonal fijo no degenerado$\mathcal{U}$. Uno tiene que hacer ese cambio por una buena razón —el plano hiperbólico y la esfera no tienen cuadrados.

El conjunto$\mathcal{U}$ en este caso juega el papel de la unidad de medida para el área y el cambio$\mathcal{U}$ requerirá la conversión de unidades de área.

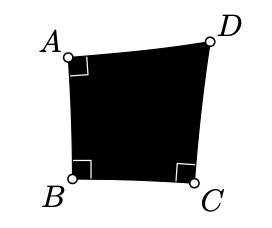
$2021-03-03 10.43.30.png$

De acuerdo con la convención estándar, el conjunto$\mathcal{U}$ se toma para que en pequeñas escalas el área se comporte como área en el plano euclidiano. Digamos, si$\mathcal{K}_a$ denota el cuadriángulo sólido$\blacksquare ABCD$ con ángulos rectos en$A$$B$,, y$C$ tal que$AB=BC=a$, entonces podemos suponer que

$\tfrac{1}{a^2}\cdot\text{area }\mathcal{K}_a\to 1 \quad \text{as} \quad a\to 0.$

Esta convención funciona igualmente bien para esferas y planos neutros, incluido el plano euclidiano. En geometría esférica equivalentemente podemos suponer que si$r$ es el radio de la esfera, entonces el área de toda la esfera es$4\cdot\pi\cdot r^2$.

Recordemos que defecto del triángulo$\triangle ABC$ se define como

Resulta que cualquier plano neutro o esfera hay un número real$k$ tal que

\[k\cdot\text{area }(\blacktriangle ABC)+\text{defect}(\triangle ABC)=0 \]

para cualquier$\triangle ABC$.

Este número$k$ se llama curvatura;$k=0$ para el plano euclidiano,$k=-1$ para el plano h,$k=1$ para la esfera unitaria, y$k=\tfrac1{r^2}$ para la esfera de radio$r$.

Dado que los ángulos del triángulo ideal desaparecen, cualquier triángulo ideal en el plano h tiene área$\pi$. De manera similar en la esfera unitaria el área del triángulo equilátero con ángulos rectos tiene área$\tfrac\pi2$; ya que toda la esfera puede subdividirse en ocho de esos triángulos, obtenemos que el área de esfera unitaria es$4\cdot\pi$.

La identidad 20.9.1 puede ser utilizada como una forma alternativa de introducir la función de área; funciona en esferas y todos los planos neutros, excepto en el plano euclidiano.