Prefacio

Introducción

El curso inicia con una revisión de varios de los resultados más elementales de la Geometría Euclidiana tradicional; de hecho, los del inicio del Libro 1 de Los Elementos, el original euclidiano. Dado que esta obra tiene alrededor de 2300 años, los derechos al original no son un problema. Durante milenios, los matemáticos han estado convencidos de que los griegos originales y las generaciones de matemáticos que los siguieron creían que la “singularidad de los paralelos” podría demostrarse a partir de “axiomas” más fundamentales sobre la geometría (lit., “medida de la tierra”) que eran tan obvios que podían asumirse con seguridad sin pruebas. El contenido estándar para un curso llamado “Geometría Moderna” implica demostrar que no es así y estudiar lo que sucede bajo una suposición diferente.

Comprender lo que los matemáticos modernos quieren decir con “prueba” data de esta época y de esta obra, Los Elementos. Muchos de nosotros estamos convencidos de que, de todas las aportaciones de los antiguos griegos al pensamiento humano moderno, sus ideas de lógica deductiva, concretadas con pruebas matemáticas, son las más importantes.

Se han escrito muchos libros y se dispone de buenos libros de texto que cubren el material de este curso. Desafortunadamente, los libros que van lo suficientemente profundo como para desarrollar bien el tema asumen un año de estudio, un semestre no es suficiente sobre todo para estudiantes con antecedentes débiles. El enfoque estándar es desarrollar primero más resultados de geometría euclidiana avanzada y eventualmente retroceder y entrar en geometría hiperbólica. Para llegar a donde necesitamos llegar, no vamos a desarrollar formalmente algunos de los resultados euclidianos avanzados que lógicamente son necesarios porque nunca llegaríamos a la parte “moderna” del nombre del curso. Volveremos y desarrollaremos, o al menos introduciremos conceptualmente, algunos de estos cuando los necesitemos tarde en el curso. Se sacrificará un compromiso considerable con la formalidad matemática para cumplir con este objetivo pero no la idea de prueba matemática en sí misma. De hecho, el objetivo más importante del curso es solidificar declaraciones probatorias dentro del marco de la geometría euclidiana. Que el contexto no sea “euclidiano” puede ser muy útil para entender el propio entorno euclidiano. Si nunca has tenido experiencia en geometría euclidiana basada en pruebas, espera que el curso sea muy difícil, tal vez incluso demasiado difícil para tu éxito sin un esfuerzo excepcional de tu parte.

Se asumirá que tienes un conocimiento práctico de la lógica elemental; por ejemplo, un uso cómodo de declaraciones universales (“por cada...” \(\forall\)) versus declaraciones existenciales (“existe...” \(\exists\)) donde cada elipsis, “...”, es en sí misma una declaración. Eso nos respalda aún más; ¿qué es una “declaración”? Se trata de una oración (en nuestro caso inglés pero cualquier idioma servirá) que tiene “valor de verdad”; tiene sentido llamarla “verdadera” o “falsa” en contraposición a, digamos, preguntas u órdenes. Estas ideas y geometría euclidiana mucho más elemental podrían darse por sentadas hasta las últimas décadas pero, lamentablemente, ya no es así. El curso tradicional de secundaria, generalmente “geometría de segundo año”, dio una formación muy diferente a la que han experimentado muchos estudiantes -incluso estudiantes fuertes con aspiraciones profesionales basadas en las matemáticas-. Creo profundamente que este tipo de estudiantes son fallidos por este “progreso” pero la realidad es lo que es. Como ejemplo concreto, uno de los mejores y más populares libros de Geometría Proyectiva (incluyendo este campus, ¡usando este mismo nombre y número de curso!) dentro de la historia reciente - es A. Seidenberg Conferencias en Geometría Proyectiva, de la Serie La Universidad en Matemáticas de Pregrado, 1962, de D. Van Nostrand Company, Inc. Del primer párrafo de la Intro:

“El propósito de este libro es proporcionar un texto para un curso de licenciatura en Geometría Proyectiva. El enfoque axiomático de esta materia es indudablemente el propio, pero parece deseable, si no es necesario, partir de lo que sabe el alumno, es decir, la geometría de secundaria, y proceder de ahí a cosas nuevas. En consecuencia, el primer capítulo está dedicado a introducir algunos de los temas principales de una forma lo más ingenua posible”.

Esa “forma ingenua como sea posible” del primer capítulo debería servir de advertencia. Yo desafiaría a más de dos alumnos de esta clase a leerla y entenderla sin alguna ayuda seria; quizás la mitad de nuestro semestre necesitaría dedicarse para llegar a la preparación que Abraham Seidenberg de UC Berkeley tenía en mente para el inicio del curso. Si no has tenido un curso de geometría euclidiana bastante tradicional basado en pruebas, encontrar un texto de geometría de secundaria más antiguo o uno de algunos de los colegios comunitarios (muchos de los cuales no han perdido el camino) para estudiar puede ser un comienzo muy útil (¡como en AHORA!) para el curso. Otra oportunidad es la increíble Khan Academy gratuita en línea que puede ofrecer esta “revisión” que puede ser mucho más que revisión pero necesaria para el éxito en este curso y para una comprensión adecuada de la geometría basada en pruebas específicamente y las matemáticas basadas en pruebas de manera más general:

https://www.khanacademy.org/math/geometry/

Este es un curso de primer año de nivel de secundaria sobre Geometría (que se basa en los elementos de Euclides). Revisita muchos de los conceptos geométricos básicos estudiados en cursos anteriores, pero los aborda con más rigor matemático. Hay un fuerte enfoque en probar teoremas y resultados a partir de postulados básicos.

Procediendo (como en todas las matemáticas formales), una “declaración” es una oración que tiene un “valor de verdad” indefinido (ojalá, significativo en el contexto) y se construyen nuevas declaraciones a partir de las existentes de varias maneras. Para una sola declaración, su negación significa cualquier reformulación de la declaración de tal manera que si era verdad, la nueva declaración es falsa e inversamente, si era falsa, la nueva afirmación es verdadera. Simbólicamente, si\(p\) es una declaración, su negación se indica por\(\sim p\) o\(\neg p\) o, con menos frecuencia,\(p^{\prime}\). Dos o más declaraciones se pueden componer en nuevas declaraciones de varias maneras; las más obvias son y y o (formalmente, conjunción y disyunción que nunca usaremos más allá de esta introducción junto con sus símbolos lógicos formales, \(\wedge\)y\(\vee\)). En el primer caso, la afirmación es verdadera si y sólo si ambas (todas, si son más de dos) declaraciones son verdaderas y, en la segunda, es verdad si y sólo si al menos una de ellas es verdadera.

Volviendo a las declaraciones universales y existenciales, sus nombres formales rara vez se usarán y sus símbolos formales\((\forall\) y\(\exists\)) nunca se utilizarán. También entendida -pero esta vez de uso frecuente- será la idea de que para probar que una declaración universal falsa solo requiere exhibir un contraejemplo concreto (un ejemplo de la afirmación que es demostrablemente falsa) o, como a veces es más esclarecedor, un conjunto de ejemplos de la afirmación con alguna propiedad común que muestre todo (¡eso es importante!) de ellos para ser falsos. Para un ejemplo no matemático, considere la afirmación, “Todos los perros son blancos”. Obviamente es falso y solo contraejemplo, exhibir un solo perro marrón (o de cualquier color que no sea blanco) demuestra que es falso como lo hace el conjunto de todos los perros marrones (ya que ese conjunto no está vacío). Un hecho menos obvio -pero totalmente estándar a lo largo de las matemáticas- a menos que se califique lo contrario, se supone que las declaraciones generales son universales Como ejemplo de geometría, “Un triángulo equilátero es equiangular” se supone que significa una afirmación sobre todos los triángulos equiláteros, no sólo alguno de ellos, de lo contrario tendría que decir algo como, “Algún triángulo equilátero es equilátero”, o equivalentemente, “Algunos triángulos equiláteros son equiláteros”, ya que el adjetivo plural “algunos” en lógica significa lo mismo que “uno o más”; es decir, “al menos uno”.

Ya siendo utilizado en el párrafo introductorio, es un “conocimiento práctico” de los enunciados condicionales (también conocidos como implicaciones); es decir, “Si..., entonces...” declaraciones donde cada “...” es una declaración. Un poco más formalmente, “Si\(p\)\(q\), entonces”, donde\(p\) (el antecedente) y\(q\) (lo consecuente) son declaraciones. En lógica formal, esto se escribe\(p \Rightarrow q\) "" (o "\(p \rightarrow q\)“) y rara vez se utilizará excepto aquí donde hace más conveniente revisar términos relevantes. En primer lugar,\(p \Rightarrow q\) "" es cierto excepto para un caso, cuando\(p\) es verdadero y\(q\) es falso. Por ello, probar una implicación se efectúa asumiendo que eso\(p\) es cierto y demostrando que, con esa suposición, también\(q\) debe ser cierto. Al primer conocimiento, esta convención puede parecer contradictoria pero la lógica del sentido común sí requiere que afirmaciones como “Si todos los perros son blancos, entonces mi perro es blanco” se consideren verdaderas aunque no tenga sentido porque, obviamente, no todos los perros son blancos sino, a pesar de que el antecedente es claramente falso, la declaración debe tomarse como verdadera. Si no estás convencido de que esa afirmación carece de sentido, considera esta ligera modificación, “Si todos los perros son blancos, entonces mi perro es negro”. Nuevamente, el antecedente es falso por lo que la afirmación se toma como verdadera pero, obviamente, sin sentido.

[Nota: Esto es desde la perspectiva de lo que se conoce como “lógica proposicional”. Este tipo de declaraciones (“cuantificadas”) se consideran ordinariamente desde la perspectiva de lo que se conoce como “lógica predicada"].

Puede recordar de la lógica que tal implicación "\(p \Rightarrow q\)" es lógicamente equivalente (es decir, una declaración es verdadera si y solo si la otra declaración es verdadera) a la declaración compuesta "\((\sim p) \vee q\)" que es verdadera si cualquiera\(\sim p\) es verdadera (es decir, \(p\)es falso) o\(q\) es cierto. Es decir, para que la implicación original sea cierta, o el antecedente\(p\) es falso o el consecuente\(q\) es verdadero, de ahí la equivalencia. Si esto no le parece familiar, es fácil probar tales afirmaciones usando tablas de verdad; es decir, confirmar directamente todos los valores de verdad posibles, en este caso, cuatro.

Atrás algunos párrafos, se utilizó la palabra “inversamente” aunque menos cuidadoso pero el uso común podría haber dicho “a la inversa”. La idea de lo contrario de una implicación es crítica en este curso y a lo largo de las matemáticas al igual que otras permutaciones de los enunciados involucrados. Considerando la implicación general:

implicación:\(p \Rightarrow q\) Las permutaciones son:

converse: Es\(q \Rightarrow p\) decir, intercambiar el antecedente y lo consecuente.

inverso: Es\(\sim p \Rightarrow \sim q\) decir, negar el antecedente y también el consecuente.

contrapositivo: Es\(\sim q \Rightarrow \sim p\) decir, tanto negar como intercambiar el antecedente y consecuente.

No es una permutación del original sino una declaración relacionada que puede o no ser cierta:

bicondicional: Es\(p \Leftrightarrow q\) decir, tanto la implicación como su contrario:\(p \Rightarrow q\) y\(q \Rightarrow p\).

Debes saber (es fácil de probar) que la implicación original y su contrapositiva son lógicamente equivalentes (una es verdadera si y sólo si la otra es verdadera) como lo son su inversa y su inversa (contrapositivo implica eso). Por último, lo bicondicional es verdadero si y solo si\(p\) y\(q\) son ambos verdaderos o ambos falsos.

De importancia crítica es el hecho de que la implicación y su contrario no son inherentemente lógicamente equivalentes (Si mi perro es blanco, ¿entonces todos los perros son blancos?) aunque suele darse el caso de que las implicaciones en matemáticas son bicondicionales; es decir, “si y sólo si” y abreviado como “iff” Por ejemplo, “Un triángulo es equilátero si y sólo si es equiangular”, o más sucintamente, “Un triángulo es equilátero si es equiangular”. A primera vista, tal afirmación no parece ningún tipo de implicación sino que hay que pensarla de manera equivalente y sin esfuerzo como, “Si un triángulo es equiangular entonces es equilátero y a la inversa; es decir, si un triángulo es equilátero entonces es equiangular”.

El “pensarlo como” puede parecer al revés pero no lo es. Si esto no está claro, es necesario examinar más cuidadosamente la posición del “si” y del “solo si” en la declaración. Deja fuera el “y solo si” para ver más fácilmente la idea. Simbólicamente, eso diría "\(p\)si\(q\)" eso es casi obviamente equivalente a “si\(q\), entonces\(p\)”. El “solo si” es un poco más difícil de entender al principio pero pensar en lo que "\(p\)solo si\(q\)" debe significar; debe significar que se\(q\) deriva de saber\(p\) o, si\(p\) es cierto, entonces\(q\) también debe ser cierto. Es decir, si\(p\), entonces\(\mathrm{q}\). De ahí la equivalencia.

Las primeras 28 proposiciones del Libro 1 original de los Elementos de Euclides no utilizan “Euclides\(5^{\text {th }}\)”, conocido como “El Postulado Paralelo”, y esas proposiciones son donde iniciaremos el curso. Los usaremos como una revisión de la geometría y de la prueba misma en el entorno geométrico familiar. El lenguaje es arcaico pero me gusta tanto la historia como la geometría. Desde una perspectiva moderna, las definiciones introductorias del griego antiguo son demasiado ingenuas y algunas de las primeras proposiciones (especialmente SAS) necesitan ser axiomas o probarse como consecuencias de otras no declaradas, pero la presentación es sorprendentemente moderna dados los milenios intermedios. La idea de esforzarse tanto por evitar “el” Postulado Paralelo (o cualquiera de las infinitamente muchas afirmaciones que son lógicamente equivalentes) en la medida de lo posible es bastante moderna en su perspectiva. “El mayor tiempo posible” es una exageración pero el objetivo es evidente y no fue respondido por un par de milenios hasta el desarrollo de la geometría hiperbólica por parte de los bolyais (en su mayoría hijo Johann) y Nikolai Lobachevski en los 1830 s.

Muchos otros teoremas que “se sienten como geometría euclidiana” también pueden probarse en geometría "neutra" o "absoluta" (que abarca tanto la geometría euclidiana como la hiperbólica) que estudiaremos en el Capítulo 2 como “Hipotenusa-Pierna”, “construcción del círculo interior de un triángulo”, y “construcción de las tangentes de un punto a un círculo” junto con muchos otros que son demostrables en este contexto (sin Postulado Paralelo) antes del Capítulo 3 donde nos especializamos utilizando la negación del Postulado Paralelo que (en conjunto con los otros axiomas de geometría neutra) es geometría hiperbólica.

Ninguna de estas geometrías es el “mundo real” en el que vivimos; es decir, en la superficie de una esfera, un caso especial de geometría elíptica. Incluso allí, muchos de los teoremas sostienen con restricciones que las cifras no son “demasiado grandes”, sea lo que sea que eso pueda significar. Este contexto puede ser útil para comprender algunos resultados (por lo que ocasionalmente se utilizará aquí) pero no deben considerarse como parte de la negación del Postulado Paralelo porque, dados los otros axiomas, surgen grandes diferencias. En una esfera, una “línea” es un “gran círculo”; es decir, cuyo plano contiene el centro de la esfera. Utilizando un globo como modelo concreto, todas las líneas longitudinales son líneas en la geometría pero todas pasan por los polos Norte y Sur por lo que incluso la más fundamental, “dos puntos determinan una línea”, necesita algún tipo de revisión. Como otro ejemplo, considere tres puntos seguidos en el ecuador (una línea en esta geometría, otros círculos de latitud NO son líneas)) A, B y C. Ahora piensa en “deslizarse” por\(C\) todo el globo para alinearse como\(C, A\), y B. Originalmente, B “se sentía como” que estaba entre A y C. Ahora bien, es A la que tiene ese sentimiento con respecto a\(C\) y B. ¿La resolución? El concepto de "entretenimiento" que está presente e importante en la geometría neutra - no existe en la geometría esférica, al menos no de la misma manera irrestricta. Aún así, pensar en triángulos esféricos y otras figuras geométricas puede ser útil para comprender la validez y/o limitaciones de los teoremas en otros entornos geométricos. Cuando no logran ser ciertas en geometría esférica, nos ayuda a pensar con más detenimiento sobre nuestras pruebas de las afirmaciones. A menudo las razones por las que fallan las pruebas explícitas son menos que obvias Un ejemplo esclarecedor: En una esfera, cualquier triángulo -como un triángulo (ideal y perfectamente) dibujado sobre un piso de concreto vertido- tiene una suma angular estrictamente mayor que\(180^{\circ} !\)

Desde una perspectiva moderna, las definiciones introductorias del griego antiguo son demasiado ingenuas y algunas de las primeras proposiciones (SAS especialmente) necesitan ser axiomas o probarse como consecuencias de otras no declaradas pero, en términos generales, la presentación es sorprendentemente moderna dados los milenios intermedios. Este es el contenido del Capítulo 1. Después de considerar algunos teoremas adicionales comunes en geometría neutra en el Capítulo 2, comenzaremos a discutir algunas propiedades y probar algunos teoremas que son exclusivos de la geometría hiperbólica en el Capítulo 3. Para la mayoría de las personas conocedoras en la primera introducción, estos pueden parecer bastante contradictorios, incluso equivocados. La competencia con la lógica deductiva formal, es decir, la prueba, hará que los resultados sean inevitables (desde ese punto de partida) pero aún así pueden tener un aire de fantasía. Hay mucho más en la geometría hiperbólica de lo que estudiaremos pero, nuevamente, solo tenemos un término así que esto solo será una breve introducción con el objetivo principal ser el desarrollo de una lectura y prueba cuidadosas en matemáticas en lugar de dominar el contenido ya sea de geometría hiperbólica o geometría euclidiana avanzada, ambos temas importantes dignos de estudio en esta etapa de tu carrera.

La validez de los axiomas de geometría hiperbólica se establece verificando la “consistencia relativa” con la geometría euclidiana; es decir, estableciendo un modelo para esta “nueva” geometría enteramente dentro de la geometría euclidiana. Es decir, si alguna vez hay que demostrar que algo es inconsistente en esta nueva geometría, significaría una inconsistencia dentro de la geometría que todos creemos, la geometría euclidiana. En realidad, este es un teorema largo y complicado de geometría euclidiana con muchas partes. Para ello, se selecciona un subconjunto del plano euclidiano dentro del cual se redefinen los constructos de geometría “normal”; es decir, dando nuevas especificaciones de cómo llamar puntos, líneas, medida de segmento de línea, etc., y relaciones entre ellos. Dentro de este escenario, cada axioma (postulado) de geometría hiperbólica debe ser probado como un teorema euclidiano; es decir, utilizando cualquiera de los axiomas y teoremas de la geometría euclidiana necesarios. Es decir, somos libres de usar puntos convencionales, líneas, etc., de todo el plano euclidiano, y todos los teoremas entre ellos, para probar cada uno de los axiomas de la geometría hiperbólica como teorema en el modelo. Muchos de los resultados necesarios en la geometría euclidiana no están cubiertos en los cursos introductorios de geometría euclidiana, por lo que tendremos que introducir y estudiar algunas de las propiedades de la geometría euclidiana que son “conocidas” pero más avanzadas que la geometría de la escuela secundaria.

Cabe señalar que este teorema de consistencia es una consecuencia trivial del Análisis Complejo (Transformaciones Fraccionales Lineales y mapeo conformacional). Sin embargo, la mayoría de los estudiantes de matemáticas no tienen ese nivel de sofisticación matemática en esta etapa (¡y muchos nunca lo harán!). Además, mucho se puede obtener de la revisión de la geometría euclidiana elemental así como del nuevo material aprendido en el proceso (inversiones en círculo especialmente). Peor aún, a veces no se prueban las ideas en Análisis Complejo sino que se refieren al conocimiento del estudiante Geometría euclidiana. No hay nada malo en esto excepto que no se puede usar en ambos sentidos; ¡el razonamiento circular es un no-no en matemáticas!

Después de argumentar que la lógica deductiva semiformal era el regalo más importante de los antiguos griegos al pensamiento humano moderno, y que la geometría es una introducción efectiva y más común (algo) formal a ese proceso, podría sorprender que el desarrollo axiomático formal no sea realizado en este curso. Es incluso peor que eso; ¡la colección de axiomas que usaremos nunca se declarará ni siquiera! El problema es que, en un desarrollo genuinamente formal, incluso la teoría de conjuntos subyacente y el análisis real, tendrían que desarrollarse axiomáticamente. Incluso dar por sentado la teoría de conjuntos ingenua y las propiedades de los números reales y enfocarse solo en la geometría requeriría un nivel de formalidad que excluiría hacer mucho más en todo el curso. Tomaremos el extremo opuesto y solo declararemos el más crítico de los axiomas pero cuánta formalidad se espera es difícil de cuantificar con precisión. Ojalá, desarrollarás rápidamente una “sensación” para ello. De hecho, tal vez tengas que “desaprender” algunas formalidades falsas; por ejemplo, en este nivel y más allá, es estándar ignorar afirmaciones que son lógicamente necesarias pero tan obvias que su inclusión sería pedante. Saber lo que es “obvio” y lo que requiere declaraciones de verificación puede ser complicado, claro; entre otros problemas, depende de la sofisticación tanto del escritor como del público objetivo.

Los términos axioma y postulado están tomando para ser intercambiables y significan declaraciones que son aceptadas sin pruebas. Uno de los “errores” de los griegos fue asumir que algunas afirmaciones son tan obviamente universalmente verdaderas que siempre son verdaderas sin pruebas y, por tanto, un punto de partida seguro. Una perspectiva más moderna es dejar completamente fuera de la mezcla el concepto de “verdad universal”. Si estamos en un escenario donde las afirmaciones son verdaderas -un llamado “modelo” de la geometría- ¿qué más debe ser cierto porque ya se ha demostrado? Si no, eso también está bien; solo estamos en algún otro escenario, quizás igualmente útil, tal vez aún más. Las mismas afirmaciones pueden o no ser ciertas pero, si lo son, requieren nuevas pruebas.

Axioma 1 - (¡Por el resto del curso!) - Dos puntos determinan una línea.

Si esto no te parece familiar, ¡probablemente estés en el rumbo equivocado! No obstante, saber realmente lo que significa es muy diferente. ¿Qué son los “puntos”? ¿Qué son las “líneas”? ¿Qué significa “determinar”?

Quizás sorprendentemente, (excepto dentro de cualquier modelo) punto y línea se tomarán como términos indefinidos restringidos por ciertos axiomas (que tampoco se declaran formalmente). Más sorprendentemente, quizás, es que en cualquier sistema axiomático, debe haber términos indefinidos o la estructura es inherentemente circular. En el nivel set, “set” y “element of a set” no están definidos. ¿Un conjunto no significa una “colección de” o algo así? Bueno, ¿qué significa “colección de”? Etc., etc. es decir, no hay lugar para detenerse así que, a lo largo de milenios, los logísticos formales han aprendido a no intentarlo. Pero, sean lo que sean, se comportan de ciertas maneras; es decir, según declaraciones llamadas axiomas. Para la teoría de conjuntos y los números reales o complejos, ni siquiera comenzaremos a tratar de decir lo que son axiomáticamente; solo los usaremos a voluntad (junto con la mayoría de los matemáticos casi todo el tiempo).

Antes de comenzar, hay algunas propiedades de un conjunto de axiomas que hay que entender.

Lo más fundamental es que necesitan ser consistentes; es decir, que no tengan contradicciones inherentes. En otras palabras, es fundamental estar seguro de que no pueden conducir a afirmaciones que puedan ser probadas y desmentidas; es decir, que se demuestre que son tanto verdaderas como falsas dentro del sistema. Tal afirmación destruiría toda la estructura.

Demostrar que no pueden surgir tales contradicciones inherentes es un desafío en sí mismo. De hecho, en un sentido muy real, ¡es una tarea imposible! Totalmente dentro de un sistema mismo, es imposible probar que los axiomas son consistentes. La prueba estándar de consistencia de un conjunto de axiomas es producir un “modelo”; una realización concreta de la situación (¡e incluso “concreto” está en el ojo del observador!) en el que todos los axiomas pueden ser probados como teoremas. Por ejemplo, si tenemos suficiente fe en el plano cartesiano ordinario (x, y), proporciona un ejemplo de un modelo para la geometría euclidiana y, con esa suposición, los axiomas de la geometría euclidiana deben ser consistentes. Para los sistemas abstractos, lo máximo que lógicamente podemos esperar es la consistencia relativa; si aceptamos que un sistema sea consistente, utilícelo para probar que otro también debe serlo.

Una propiedad menos crítica pero deseable es que los axiomas sean independientes. Esto significa que no es posible probar ninguno de ellos usando solo los demás. No tener esta propiedad no destruiría el sistema pero definitivamente se prefiere. Cuanto menos y más fundamentales sean los axiomas, más “limpia” es la estructura. Podríamos haber encontrado el Teorema de Pitágoras en sexto o séptimo grado pero no se presentó como el Axioma de Pitágoras solo porque aún no podíamos entender una prueba. La idea era que se tomara como verdad sin nuestra prueba pero no sin la prueba de alguien. Los axiomas no son simplemente “sacados del aire”; la sabia elección de ellos es un proceso muy sofisticado y no vamos a empezar a intentarlo. Ni siquiera intentaremos enumerarlos, pero algunas opciones famosas están fácilmente disponibles y serán referenciadas a continuación.

Una tercera propiedad que podría tener un sistema es que los axiomas sean categóricos. Esta no siempre es una propiedad deseable ya que implica que estamos tratando en circunstancias muy especializadas cuando, en matemáticas, muchas veces queremos estudiar propiedades que se aplican a muchas situaciones inherentemente diferentes. Por ejemplo, un “grupo” en matemáticas es un término especializado que se aplica a muchas estructuras diferentes que se ajustan a los axiomas del grupo pero, si les sumamos que el grupo tiene exactamente siete elementos, el conjunto de axiomas se vuelve categórico. En un sentido muy real, sólo hay uno de esos grupos. Es decir, si el conjunto de axiomas es categórico, todos los “modelos” del escenario pueden verse como formas exteriormente diferentes de exactamente lo mismo. En la jerga, todos los modelos son “isomórficos”. En el lado positivo, si se sabe que un conjunto de axiomas es categórico, un teorema probado en el contexto de un modelo también debe ser válido en todos los demás modelos. Como ejemplo, si estás familiarizado con la prueba “analítica” versus la prueba “sintética” en la geometría euclidiana, saber que los axiomas son categóricos nos asegura que cualquiera de las pruebas es suficiente. Un teorema en cualquier modelo es un teorema en la geometría. (Véase el capítulo 4.)

¿Qué es un modelo del escenario? Mantengámoslo en términos de geometría plana. Una geometría es un conjunto abstracto de elementos llamados “puntos”, ciertos subconjuntos abstractos de los cuales se llaman “líneas” y quizás otros conjuntos especiales asumiendo que satisfacen ciertas propiedades de confinamiento llamadas axiomas. Un modelo para esta geometría es, en cierto sentido, casi lo contrario. Se trata de un conjunto muy concreto, cuyos elementos se denominan puntos, subconjuntos concretos de estos puntos llamados líneas y círculos, etc., y todos los axiomas de la geometría (es decir, declaraciones asumidas sin prueba en la geometría) se prueban como teoremas en el modelo. En ese punto, todos los teoremas de la geometría se convierten también en teoremas en el modelo; es decir, ya han sido probados.

Aquí hay dos famosos conjuntos de axiomas que están fácilmente disponibles:

• Axiomas de Hilbert para Geometría Euclidiana:

• Axiomas de Birkhoff para Geometría Euclidiana:

Nota: De estos conjuntos formales de axiomas (que no usaremos formalmente), solo el de Birkhoff (1959) incluye lo que se conoce como Postulado Gobernante y Postulado Transportador. Sin embargo, el de Hilbert (1899 revisado en 1902) implica resultados consistentes con ellos [Google: Desargues/Pappus/Field y/o ver Blumenthal,\(A\) Modern View of Geometry, the V. H. Freeman & Co, 1961] y fueron revisados para incluirlos por Saunders MacLane en 1923. Estos no fueron utilizados por los griegos (aunque algunas de las mismas ideas estuvieron presentes pero se expresaron en términos de comparaciones de segmentos de línea (para longitud), polígonos (para área) y ángulos (para medida de ángulo). Los incluiremos pero los usaremos de manera algo informal de la siguiente manera:

Postulado de Regla: Hay una correspondencia 1-1 entre los puntos de una línea dada y los números reales que se comportan de “maneras agradables”; es decir, dada una distancia y una dirección, hay un punto único determinado y viceversa. Es decir, una vez que la línea está “coordinatizada”, cada punto corresponde a un número real único, y esta asociación de segmentos de línea es consistente con la aritmética de números reales. Para los segmentos de línea, esta distancia entre sus puntos finales se llama la medida del segmento de línea pero la palabra “medida” es engañosa; no hay medición involucrada ya que toda la medición es aproximada y estas se toman para ser infinitamente precisas.

Postulado del Transportador: Hay una correspondencia 1-1 entre los ángulos que parten de un rayo dado y los números reales de un intervalo cerrado\([0,180]\) (\([-90,90]\)o\([0, \pi]\) o o\([-\pi / 2, \pi / 2]\) o cualquier otro, incluidos los que puedan ser razonables pero casi nunca se usan como\([0,100]\)) tal que, dado un tamaño de ángulo y una dirección, hay un rayo único determinado y viceversa. Una vez que el semicírculo está “coordinado”, cada rayo corresponde a un número real único del intervalo y, nuevamente, esta asociación es consistente con la aritmética de los números reales. A este número asociado se le llama la medida del ángulo pero, nuevamente, no hay medición involucrada. Siempre se asume la precisión infinita a menos que se indique lo contrario (casi nunca).

Por última vez, estas ideas (especialmente sus nombres) pueden ser un poco engañosas; no hay ninguna medición real que se esté llevando a cabo ya que eso sería inherentemente aproximado. Se trata únicamente de abstracciones teóricas. Se supone que todo es infinitamente preciso, lo que nunca es posible en situaciones de medición. Además, a menos que se indique lo contrario, se esperará de usted una precisión infinita por lo que las calculadoras serán de poca ayuda excepto como manta de seguridad. A excepción de los exámenes mayores, no estarán prohibidos pero se espera que las respuestas sean precisas; por ejemplo, no\(\pi\)\(3.14159,2 / 7\) es\(3.14\) ni no\(0.2857\), etc. Las respuestas decimales son aceptables solo si son precisas - decimal aproximaciones no recibirán crédito completo. Las fracciones ordinarias simplificadas bastarán para el curso y, de hecho, se prefieren cuando proceda. Las calculadoras, los celulares, y similares estarán prohibidos a partir de la mitad de período y final porque se han vuelto demasiado “inteligentes”; es decir, pueden registrar información y darle acceso a información que debe estar en su cabeza para poder pensar de manera efectiva.

¿Cómo podemos operar axiomáticamente sin afirmar nunca la mayoría de los axiomas explícitamente? Ojalá, se te ocurra la idea a medida que avancemos. Una de las ideas importantes sobre las que vamos a ser algo “descuidados” es la de “entretenimiento” de puntos en una línea pero tiene que “estar ahí” nos preocupemos o no. Otra son las consideraciones de continuidad. Digamos, por ejemplo, que un segmento de línea está determinado por un punto dentro de un círculo y otro fuera de él. Debería ser obvio -y lo daremos por sentado- que hay un punto de intersección de ese segmento y el círculo. Se necesitan axiomas formales pero serán ignorados.

La misma idea se aplica a las definiciones. Son absolutamente críticos y sin embargo muchos de ellos no se darán en el curso, al menos no explícitamente. Si hay alguna duda sobre lo que es cierto "por definición" sobre algún objeto nombrado de algún tipo, pregunte, y tome nota cuidadosa de ello en su propio glosario personal. Afirmar que una propiedad de alguna estructura geométrica es cierta por definición cuando no forma parte de la definición, sino que se ha demostrado en cambio, es un grave error así que ten cuidado. Si hay alguna ambigüedad, incluya también el nombre de la palabra a la que se hace referencia; por ejemplo, “por definición de rectángulo” en lugar de simplemente “por definición”. [¿Cuál es la definición de rectángulo? Un cuadrilátero con todos los ángulos siendo ángulos rectos. Nada más. Cualquier otra cosa debe ser probada.]

Las abreviaturas son otro lugar donde se debe ejercer cuidado en el sentido de que sus formas “en toda regla” tienen que estar claramente en mente. Es decir, no se debe usar una abreviatura a menos que tanto el escritor como el lector puedan expandirla de manera equivalente y sin esfuerzo. Un buen ejemplo en geometría es SAS. A menos que tengas habilidades de inglés o matemáticas débiles, puedes leerlo inmediatamente como “Side-Angle-Side”. Eso no es lo que se entiende por “expandirlo”; eso es solo la abreviatura. SAS es una declaración; es decir, es una frase completa (en nuestro caso, en inglés) que tiene valor de verdad. Además, se trata de una declaración universal; en este caso, una afirmación sobre todos los triángulos que cumplen con las condiciones SAS. Es común en geometría -y en entornos matemáticos de manera más general- asumir la universalidad (es decir, “por cada...”) de declaraciones que “suenan así”. En general, no se debe usar una abreviatura a menos que pueda expandirla sin ambigüedades a pedido y no como algún tipo de respuesta literal, de memoria sino exactamente el mismo contenido matemático con tan pocos símbolos y/o figuras matemáticas como sea factible y consistente con la expansión que cualquier otro conocedor practicante se lo daría. Además de ser una declaración universal, SAS es un ejemplo de una declaración o implicación condicional; es decir, es una declaración “si..., entonces...” como se discutió anteriormente siendo la SAS sólo una abreviatura de su hipótesis, no de su conclusión, y mucho menos de toda la implicación.

SAS: Si dos triángulos tienen dos pares de lados congruentes y los ángulos incluidos por estos pares de lados congruentes, entonces los triángulos son congruentes.

¿Es verdad? Al menos tiene sentido preguntar así que es una declaración! Explicando su significado a alguien que no sabe lo que significa, sería más claro si se apoyara en una buena figura con las condiciones debidamente señaladas. Eso, sin embargo, debe ser una trivialidad para la persona que utiliza la declaración y para la persona que la está leyendo o escuchando; de lo contrario, no se debería utilizar en absoluto la abreviatura. Sus cuadros tendrían triángulos de diferentes formas (pero ninguno debería parecer especializado; es decir, no triángulos rectos, no isósceles, etc.) y probablemente estarían etiquetados de manera diferente pero estarían comunicando exactamente la misma idea. Una cosa que probablemente sería lo mismo sería el uso de “marcas de congruencia”, indicadores estándar de “marca de verificación” de que los segmentos de línea o ángulos son congruentes y una marca especial para ángulos rectos. ¡ÚSALOS! Desafortunadamente, mi software de gráficos más potente, Cenicienta, no los incluye así que habrá momentos en los que necesitarás agregarlos en ti mismo. Eso debería ser fácil de hacer desde el contexto. Otro punto, puede estar acostumbrado a ver tales declaraciones presentadas artificialmente como:

Dado:\(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), y\(\angle \mathrm{A} \cong \angle \mathrm{E}\) (o\(\angle \mathrm{BAC} \cong \angle \mathrm{FEG}\))

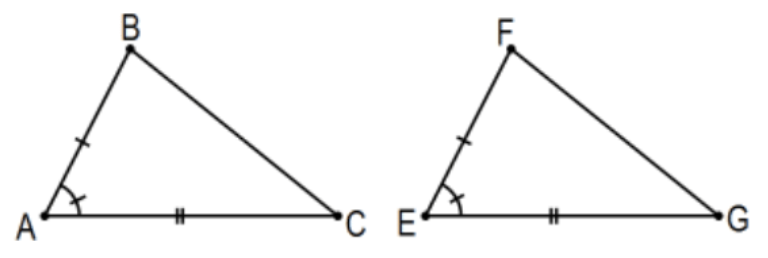
Conclusión:\(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\)

Nota: Otro (¡y peor!) limitación de mi software es que es difícil y distorsiona el espaciado entre líneas poner barras matemáticamente apropiadas sobre segmentos de línea\((\overline{\mathrm{AB}})\), flechas sobre rayos\((\overline{\mathrm{AB}}\) o\(\overleftarrow{\mathrm{BA}})\), flechas de dos puntas sobre líneas\((\overleftrightarrow{\mathrm{AB}})\) y arcos sobre arcos \((\overparen{\mathrm{AB}})\)cuando se indica por dos puntos, generalmente letras inglesas en mayúscula. Úselos en tu trabajo de manera consistente y correcta. También tenga cuidado con el “orden correspondiente”. Por ejemplo, en lo anterior, no tendríamos razón para sospechar eso\(\triangle \mathrm{ABC} \cong \triangle \mathrm{FEG}\) sino que\(\triangle \mathrm{ABC} \cong \triangle \mathrm{EFG}\) es equivalente al original. Nota: Como se mencionó anteriormente, esto es ahora una declaración o implicación condicional (universal) (es decir, si... entonces...), pero muchas veces no están así declaradas en matemáticas. Deberías poder hacer sin esfuerzo la traducción en una declaración equivalente que sí tenga esa forma y reconocer la universalidad cuando eso está implícito.

Una característica artificial a la que podría estar acostumbrado es la llamada “prueba T”; declaraciones cuidadosamente emparejadas con las razones correspondientes por las que las declaraciones son verdaderas en el contexto de la prueba. Si te sientes más cómodo con eso, siéntete libre de usar la estructura pero en realidad es solo una técnica pedagógica para convencer a los estudiantes principiantes de matemáticas de que si se hace una declaración sin una razón de apoyo (podría entenderse pero no declararse explícitamente), no es una prueba. ¿Cierto? Quizás, pero no probado.

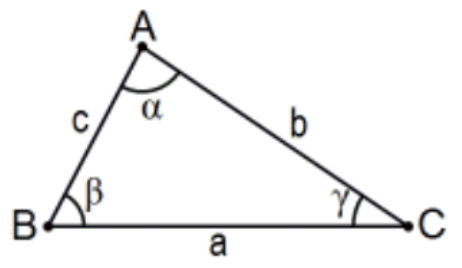
Otro detalle que se utilizará, y se le anima a usar también, es la notación estándar, algunos de los cuales son obligatorios y algunos de los cuales solo se prefieren. (Esa preferencia puede o no ser estándar fuera de los Estados Unidos). Los puntos se indicarán con letras inglesas mayúsculas y los vértices de un polígono deben enumerarse en orden secuencial (en sentido horario o antihorario).

Asimismo, los vértices correspondientes de los polígonos correspondientes (generalmente congruentes o similares pero no necesariamente) deben enumerarse en el orden correspondiente. Una variable escrita dentro de un ángulo indica la medida del ángulo -es decir, su tamaño de ángulo- no un nombre para el ángulo en sí así que NO indique un ángulo usando su tamaño en lugar de su nombre, varios ángulos pueden tener el mismo tamaño pero, obviamente, nombres diferentes.

Una convención conveniente, pero lejos de ser estándar, es usar la letra griega minúscula correspondiente para la medida de un ángulo del mismo nombre inglés. Es decir,\(\mathrm{m}(\angle \mathrm{A})\) a menudo se indicará\(\alpha, \mathrm{m}(\angle \mathrm{B})\) por\(\beta\),\(\mathrm{m}(\angle \mathrm{C})\) por\(\gamma\) (porque es el siguiente en el alfabeto griego), etc., y utilizar letras minúsculas en inglés para indicar la medida de un lado y muchas veces serán las mismas letra (pero minúscula) del vértice opuesto. El Bloc de Dibujo de Geometer “rellena” automáticamente los indicadores de medida de ángulo. NO hagas eso en tu trabajo; no es de uso estándar. Otro comentario sobre el uso, las entidades geométricas como ángulos, segmentos de línea y polígonos que son (informalmente hablando) del mismo tamaño y forma se dice que son congruentes, a diferencia de “iguales”, pero medidas\((\alpha, \beta, \mathrm{a}, \mathrm{b}\), etc.) son números reales por lo que, si son iguales, los apropiados palabra es “igual”. Este cuidado con las palabras (no compartidas por todos los geometros) proviene de su naturaleza subyacente como conjuntos de puntos. Los conjuntos son iguales si y solo si tienen los mismos elementos por lo que la consistencia requiere que, por ejemplo,\(\angle \mathrm{A}=\angle \mathrm{B}\) implicaría que los dos ángulos (unión de dos rayos con un punto inicial común) fueran exactamente los mismos dos rayos, no dos ángulos del mismo tamaño que probablemente fue la intención ; en cambio expresarlo simbólicamente como\(\angle A \cong \angle B\) y leerlo como “ángulo\(A\) es congruente con ángulo\(B\)”.

Para tener una idea de cómo va a funcionar esta prueba formal/informal, a continuación se presentan elementos de un primer cuestionario genérico junto con soluciones sugeridas (que se parecen mucho a los ítems del Conjunto de Problemas 1, en adelante PS 1). Las instrucciones comenzaron simplemente con, “Todos los ítems se relacionan con el triángulo isósceles dado”\(\triangle \mathrm{ABC}\). Implicado, por supuesto, es lo que significa isósceles, incluso el triángulo mismo. Hay muchos términos “familiares” que se usan aquí y a lo largo del curso, términos como “es perpendicular a”, “rayo”, “bisectriz angular”, ASA y SSS. Ojalá que estas ideas no sean nuevas, aunque serán revisadas. Uno que usaremos que es común pero no universal es “cpctc”, “las partes correspondientes de triángulos congruentes son congruentes”. Equivalentemente, se podría decir “por congruencia de triángulos” (o de figuras geométricas congruentes de manera más general) pero cpctc es tan práctico y de uso tan común que animo su uso. Nuevamente, hazte un glosario preciso de términos sobre los que tengas alguna duda (después de preguntar si hay algo de lo que no estés seguro).

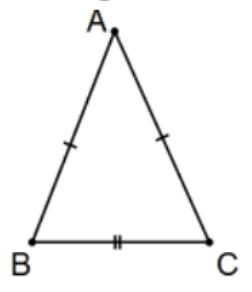
Todos los ítems se relacionan con el triángulo isósceles dado\(\triangle \mathrm{ABC}\) con ángulos de base en\(B\) y\(\mathrm{C}\).

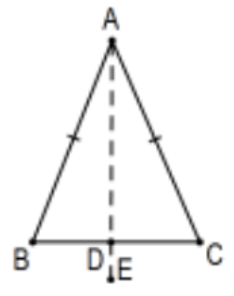
1. Indicar en el boceto toda la información dada de la manera estándar. Igualmente importante, indican nada más que la información dada.

Solución: Agregar marcas de congruencia coincidentes, “marcas de marca” a los segmentos\(A B\) y\(A C\).

2. Supongamos que ese punto\(D\) es el punto determinado por la bisectriz de\(\angle A\). \(\angle B \cong \angle C\)Demuéstralo.

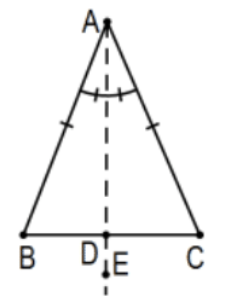
Solución:\(\mathrm{AB} \cong \mathrm{AC}\) por definición de isósceles (o “dado”) y\(\angle \mathrm{BAD} \cong \angle \mathrm{CAD}\) por definición de ángulo bisectriz (o “dado”). Por lo tanto,\(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) por SAS y\(\angle \mathrm{B} \cong \angle \mathrm{C}\) por cpctc. [Nota: ¿Qué pasó con lo\(\mathrm{AD} \cong \mathrm{AD}\) necesario\(\mathrm{SAS}\)? Formalmente, es propiedad reflexiva de la congruencia pero no se moleste. ¿No es obviamente cierto?!]

3. Supongamos que el punto\(\mathrm{D}\) es el punto medio del segmento de línea\(B C\). \(\angle B \cong \angle C\)Demuéstralo.

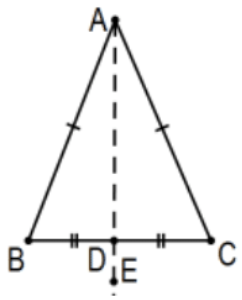
Solución:\(\mathrm{AB} \cong \mathrm{AC}\) por definición y\(\mathrm{BD} \cong \mathrm{CD}\) por definición de punto medio (o “dado”). Por lo tanto,\(\triangle \mathrm{BAD} \cong \triangle \mathrm{CAD}\) por\(\mathrm{SSS}\) y\(\angle \mathrm{B} \cong \angle \mathrm{C}\) por cpctc.

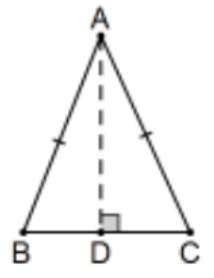
4. Supongamos que la línea DE es la bisectriz perpendicular del segmento de línea BC. No pruebes nada más que explicar por qué una fácil hipotenusa-pierna “prueba” que\(\angle \mathrm{B} \cong \angle \mathrm{C}\) es falaz.

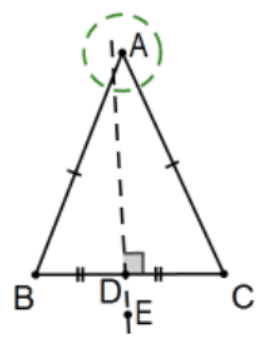
Respuesta: Por lo que sabemos en este punto, el punto A no necesita estar en la línea DE.
(El círculo en el vértice A muestra cómo se puede dibujar la figura para enfatizar esto). Es decir, la “prueba” supone que\(\mathrm{A} \in \mathrm{DE}\) sin antes probar ese hecho.

Prueba válida: Supongamos que\(\mathrm{D}\) es el pie de la perpendicular de\(A\) a la línea\(B C\) (es decir, no hay marcas que\(B D \cong C D)\). Ahora, por Hyp-Leg,\(\triangle \mathrm{ABD} \cong \triangle \mathrm{ACD}\) y\(\angle \mathrm{B} \cong \angle \mathrm{C}\) por cpctc.

Nota: El problema de #4 es una idea muy importante. Una vez que se determina una entidad (y la bisectriz perpendicular de un segmento de línea determina completamente la línea) todas las demás propiedades sobre ella deben probarse o la situación está “sobredeterminada”; es decir, la información se asume sin pruebas y posiblemente incluso podría ser falsa. Eso es casi tan malo como se pone en “prueba”. De hecho, es mejor decir “no tengo idea de cómo probarlo”.

5. Solo usando\(\triangle \mathrm{ABC}\) (es decir, sin puntos o líneas auxiliares), probar\(\angle \mathrm{B} \cong \angle \mathrm{C}\).

Solución:\(\mathrm{AB} \cong \mathrm{AC}\) por definición y\(\mathrm{BC} \cong \mathrm{CB}\). Por lo tanto,\(\triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\) por\(\mathrm{SSS}\) y\(\angle B \cong \angle C\) por cpctc. [Es decir, el triángulo es congruente consigo mismo usando una correspondencia diferente.] Ya que\(\angle \mathrm{BAC} \cong \angle \mathrm{CAB}, \triangle \mathrm{BAC} \cong \triangle \mathrm{CAB}\)\(\mathrm{SAS}\) por también.

Nota: Las dos pruebas de #5 son un poco más sutiles de lo que parecen. La congruencia de las figuras geométricas, en nuestra interpretación, se ha supuesto que está en su forma de “geometría pura”; es decir, como un término indefinido sujeto a algunos axiomas (aunque no declarados). Por ejemplo, la congruencia es (entre otras cosas) una relación de equivalencia; es decir, es reflexiva, simétrica y transitiva. Más explícitamente:

i. La figura\(\mathrm{F}\) es congruente con la figura\(\mathrm{F}\),

ii. Si la Figura\(\mathrm{F}\) es congruente con la Figura\(\mathrm{G}\), entonces la Figura\(\mathrm{G}\) es congruente con la Figura\(\mathrm{F}\), y

iii. Si la Figura\(\mathrm{F}\) es congruente con la Figura\(\mathrm{G}\) y la Figura\(\mathrm{G}\) es congruente con la Figura\(\mathrm{H}\), entonces la Figura\(\mathrm{F}\) es congruente con la Figura H.

En la\(\mathrm{SSS}\) prueba, asumimos\(\mathrm{BC} \cong \mathrm{CB}\) sin pruebas y su instinto (¿quizás enseñanza pasada?) lo llamaría cierto por la propiedad reflexiva de la congruencia. No lo es, sin embargo, porque la orientación se invierte. Una forma menos “pura” de geometría (por ejemplo, incluyendo los Postulados Regla y Transportador como nosotros) define la congruencia, y no entre figuras geométricas específicas, sino de todo el conjunto de puntos de la geometría. Formalmente, en este contexto, se definiría una congruencia como una correspondencia uno a uno de todo el plano que preserva la distancia (medida sin signo) entre dos puntos cualesquiera correspondientes y el tamaño de dos ángulos correspondientes cualesquiera. Por ejemplo,\(\mathrm{BC} \cong \mathrm{CB}\) porque la reflexión en la bisectriz perpendicular del segmento\(\mathrm{BC}\) es una congruencia que lleva segmento\(\mathrm{BC}\) a segmento\(\mathrm{CB}\) incluyendo todo el triángulo en cuestión sobre sí mismo pero con una nueva correspondencia. De igual manera para la prueba SAS, la reflexión en la línea de la bisectriz de ángulo\(\angle \mathrm{BAC}\) es la congruencia necesaria. Otra congruencia con la que probablemente estés familiarizado es la rotación alrededor de un solo punto y todas las composiciones de estos dos. En la geometría euclidiana, la traducción por un vector (un segmento de línea dirigida) es otro, a veces llamado “deslizamiento” en los libros elementales. ¿Hay otros? La respuesta es “no” pero no vamos a probar ese hecho en este curso.

A excepción de las traducciones (que necesitan paralelismos únicos), estas son también congruencias en geometría neutra (o absoluta); es decir, sin referencia al\(5^{\text {th }}\) Postulado de Euclides que nos da geometría euclidiana por lo que estas afirmaciones son ciertas tanto en la geometría euclidiana como en la hiperbólica aunque podamos estar “pensando” solo en la geometría euclidiana (¡y todavía no tenemos idea de lo que podría ser la geometría hiperbólica!).

Una última complejidad que a menudo se pasa por alto en las clases introductorias de geometría es que, para la independencia de los axiomas, las declaraciones de congruencia (es decir, SAS, SSS, ASA, AAS e Hipotenuse-Leg) no son “axiomas”, al menos no la mayoría de ellos. Aunque los griegos no se dieron cuenta, uno de estos (o algo equivalente) debe tomarse como axioma y el resto son teoremas, declaraciones condicionales por probar.

Esa última afirmación no es del todo cierta pero casi. Por ejemplo, en los axiomas de Hilbert, se describe axiomáticamente la congruencia de segmentos y ángulos y la congruencia de figuras geométricas (restringidas a las conectadas que consisten en segmentos y ángulos) se definen como congruentes si hay una correspondencia uno a uno de sus puntos de tal manera que todos los segmentos y los ángulos corresponden y son congruentes. Con esta restricción, su axioma básico no es del todo\(\mathrm{SAS}\); incluye la congruencia de los dos ángulos faltantes pero omite la congruencia del lado faltante y prueba el SAS completo como teorema. Eso es tan cercano como para ser casi trivial a excepción de la idea de mantener el conjunto de axiomas en el mínimo absoluto necesario. [Ver libro clásico de Hilbert 1902, Fundamentos de la Geometría, Corte Abierta Publishing Co., Axioma IV, 6 y Teorema 10.]

Tomaremos SAS como axioma y lo usaremos para probar los demás aunque, por ejemplo, se podrían usar SS en su lugar. Si bien SSS se declarará de manera independiente, realmente lo es, “Si SAS, entonces SSS”. En términos de lógica formal (e ignorando la naturaleza universal entendida de la situación); es decir, “Por cada... “, ante el antecedente y nuevamente ante el consecuente en la implicación, “Si\((p \Rightarrow q)\), entonces\((r \Rightarrow s)\) “, o completamente"\((p \Rightarrow q) \Rightarrow(r \Rightarrow s)\)”. En tal situación, simplemente asumimos la verdad de la afirmación\(r\) y de alguna manera demostramos que la afirmación también\(s\) debe ser cierta. En el proceso de probar\(s\), se esperaría que en algún lugar a lo largo de la línea, quizá varias veces, se\(p \Rightarrow q\) utilizaría la supuesta verdad de cualquier ocurrencia de.

De hecho, es más complicado que eso. En realidad, dice que “Si todos los axiomas de geometría neutra incluyendo SAS y teoremas previamente probados son ciertos, entonces SSS, también es cierto”. De manera más general, a lo largo de las matemáticas formales, esa es la idea: Se utiliza una gran colección de “cosas” para probar alguna nueva declaración condicional. No se menciona nada de ese complicado antecedente, sólo el antecedente de la nueva declaración condicional que se va a probar. Como se mencionó anteriormente, bien podríamos asumir\(S S S\) como nuestro axioma y usarlo para probar SAS. Centrándose solo en los conceptos de congruencia, eso hace que la declaración condicional “Si SSS, entonces SAS” sea la inversa de “Si SAS, luego SSS”. En ese caso, si tuviéramos que probar la declaración, simplemente diríamos: “Probar SAS”. Para ello, tendríamos que descartar cualquier afirmación que pensáramos que eran ciertas porque se habían probado usando SAS, y de alguna manera construir una prueba usando SSS para demostrar que los dos triángulos con la hipótesis SAS son, de hecho, congruentes. Es decir, partimos de dos triángulos que satisfacen las hipótesis de SAS (NO la hipótesis de\(\mathrm{SSS}\)) y prueban que los triángulos son congruentes. Para ello, la configuración podría verse exactamente como el SAS que vimos antes:

Dado:\(\overline{\mathrm{AB}} \cong \overline{\mathrm{EF}}, \overline{\mathrm{AC}} \cong \overline{\mathrm{EG}}\), y\(\angle \mathrm{A} \cong \angle \mathrm{E}\) (o\(\angle \mathrm{BAC} \cong \angle \mathrm{FEG})\)

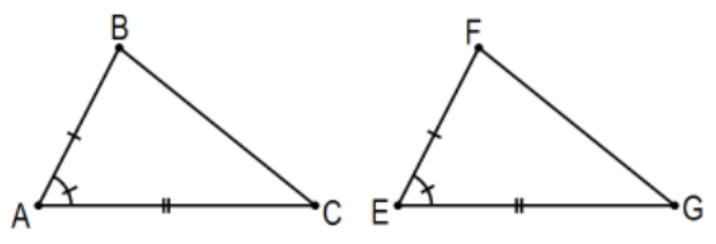
Conclusión:\(\triangle \mathrm{BAC} \cong \triangle \mathrm{FEG}\).

¿Dónde está el SSS? Siempre y donde sea tengamos las condiciones de SSS para dos triángulos (no estos dos (!) , al menos aún no), estamos para concluir que esos triángulos son congruentes. Para probar el resultado, necesitamos construir de alguna manera triángulos que sí satisfagan las condiciones de SSS como puente para demostrar que estos dos también son congruentes. Cómo hacerlo puede o no ser fácil dependiendo de la experiencia y creatividad matemática de uno. Sin embargo, hagamos lo que hagamos, debemos tener cuidado de no usar ningún teorema que se demostró usando SAS o tenemos un razonamiento circular claro, aunque no intencional. En esta etapa eso es fácil de hacer ya que no hemos probado ningún teorema excepto la congruencia de los ángulos base de los triángulos isósceles y sí ofrecimos una prueba SSS para ese hecho (que de todos modos no necesitamos). Para ver cómo esto podría funcionar, introducimos otro concepto familiar:

Las “herramientas” permitidas son una recta sin marcar (una realización del Axioma 1) y una brújula (una realización de “conocer” un círculo dado un punto para un centro y un segmento de línea o su longitud para un radio). Estas suelen denominarse las “herramientas euclidianas” pero (ya que son realizaciones artificiales de la consecuencia abstracta de los axiomas de la geometría neutra) se supone que están disponibles a lo largo del curso, geometría euclidiana o no. Nuevos puntos, líneas, etc., identificados por ellos se dirá que existen “por construcción”.

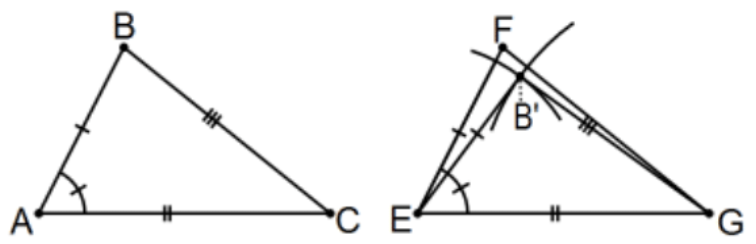
Prueba: Construir el punto\(\mathrm{B}^{\prime}\) como la intersección apropiada de (E; AB), el círculo con centro en\(\mathrm{E}\) de radio\(\mathrm{AB}\), y (G; CB), el círculo con centro en\(G\) de radio CB. Ahora tenemos un nuevo triángulo con\(\triangle \mathrm{EB}^{\prime} \mathrm{G} \cong \triangle \mathrm{ABC}\) por SSS ya que tenemos tres pares de lados congruentes “por construcción”. Ahora\(\angle B^{\prime} E G \cong \angle B A C\) porque las partes correspondientes de los triángulos congruentes son congruentes (cpctc). Por hipótesis,\(\angle B A C \cong \angle F E G\) así, por transitividad de congruencia,\(\angle B^{\prime} E G \cong \angle F E G\). Por el Postulado Transtractor, rayo\(\mathrm{EB}^{\prime}\) y rayo\(E F\) son exactamente el mismo rayo. Además,\(\mathrm{EB}^{\prime} \cong A B\) por construcción y se le dio que\(\mathrm{AB} \cong \mathrm{EF}\) así, por la transitividad,\(\mathrm{EB}^{\prime} \cong \mathrm{EF}\) así, por el Postulado Gobernante,\(F\) y\(\mathrm{B}^{\prime}\) son exactamente el mismo punto\(\left(F=B^{\prime}\right)\). Por lo tanto, los triángulos originales son congruentes porque ya sabíamos que eran congruentes, solo tenemos otro nombre para uno de los puntos. QED.

Para más información sobre el tema, consulte el Ex 22 al final del Conjunto de problemas 1 (en adelante se indica PS 1, #22).