8: Entrenamiento de una Red Neuronal

En lo que sigue, vamos a analizar el proceso de entrenamiento en una RNA de dos capas (ver figura 3). La red consta de una capa de entrada (correspondiente a \(l=0\), con dos neuronas), una capa intermedia oculta (correspondiente a \(l=1\), con tres neuronas) y la capa de salida (\(l=2\) y dos neuronas). El objetivo es calcular los pesos de la RNA, utilizando el algoritmo de retropropagación de la siguiente forma:

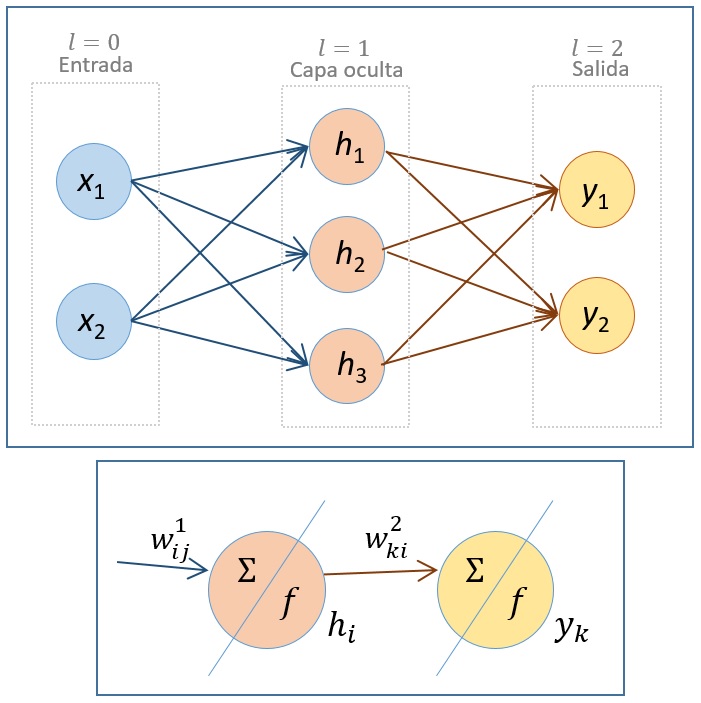
• Las entradas (en \(l=0\)), \(\textbf{x}=(x_1,x_2)^T\) son valores constantes. Vamos a denotar por \(h_i\) la salida de la neurona \(i\) de la capa \(l=1\), que serán a su vez entradas de la capa \(l=2\). Análogamente, denotamos por \(y_1\) e \(y_2\) las salidas de la capa \(l=2\) (salidas de la RNA).
• Los parámetros que debemos ajustar son los pesos (enlaces entre neuronas de diferentes capas). Se denotan por \(w^{l}_{ij}\), donde el superíndice \(l\) hace referencia a la capa a la que llega y los subíndices \(i\) y \(j\) a las neuronas de las capas \(l\) y \(l-1\), respectivamente, que conecta este peso.
• En las neuronas de la capa oculta y de la capa de salida se realizan dos procesos:
  • El primero, que simbolizamos con \(\Sigma\), corresponde en ambas capas a la combinación lineal de la salida de la capa anterior con los pesos correspondientes. Esto es:
    • En la neurona \(i\) \((i=1,2,3)\) de la capa \(l=1\): \(a^{1}_i=x_1w^1_{i1}+x_2w^1_{i2}\).
    • En la neurona \(k\) \((k=1,2)\) de la capa \(l=2\): \(a^{2}_k=h_1w^2_{k1}+h_2w^2_{k2}+h_3w^2_{k3}\).
  • El segundo, que represintamos en la figura con \(f\), corresponde a la función de activación que suponemos que es la misma para \(l=1,2\): \[\sigma(u) = \dfrac{1}{1+e^{-u}}\] Recordemos que la derivada de esta función es: \[\sigma ' (u) = \dfrac{e^{-u}}{(1+e^{-u})^2}=\sigma(u)(1-\sigma(u))\] Entonces, tenemos que las salidas de cada capa son:
    • \(h_i = \sigma(a^{1}_i)\), \(i=1,2,3\)
    • \(y_k = \sigma(a^{2}_k)\), \(k=1,2\)
• Definimos la función de pérdida o de error, como se hace usualmente, mediante la desviación cuadrática media \[L(y_1,y_2)=\frac{1}{2} \sum_{k=1}^{2} \left( y_k -t_k \right)^2\] siendo \(t_k\) (\(k=1,2\)) los valores deseados correspondientes a cada salida \(y_k\) de la RNA.

Puesto que nuestro objetivo es minimimar la función de pérdida, debemos buscar los pesos que lo consiguen, utilizando el algoritmo de retropropagación. Se trata de un proceso iterativo en el que se parte de unos valores iniciales para los pesos y estos se van modificando mediante el método del gradiente descendiente. Con los valores iniciales de los pesos, a partir de los valores \(\bf{x}\) se calculan los de \(\bf{a^1}, \bf{h}, \bf{a^2}\) e \(\bf{y}\). Con ellos, partiendo de la capa de salida, vamos hacia atrás:

1. Aplicamos la regla de la cadena \[\dfrac{\partial L}{\partial w^{2}_{ki}} \rightarrow \dfrac{\partial L}{\partial y_k}\dfrac{\partial y_k}{\partial a^{2}_k}\dfrac{\partial a^{2}_k}{\partial w^{2}_{ki}}\] con \((k=1,2)\):
   • \(\dfrac{\partial }{\partial w^{2}_{ki}}a^{2}_{k}(w^2_{k1},w^2_{k2},w^2_{k3})=h_i \quad (i=1,2,3)\)
   • \(\dfrac{\partial y_k}{\partial a^{2}_k} = \dfrac{\partial}{\partial a^{2}_{k}} \sigma (a^{2}_{k})=\sigma(a^{2}_{k})(1-\sigma(a^{2}_{k}))=y_k(1-y_k)\)
   • \(\dfrac{\partial }{\partial y_k}L(y_1,y_2) = \left( y_k -t_k \right)\)

   Resulta, sustituyendo: \[\dfrac{\partial L}{\partial w^{2}_{ki}} \rightarrow \left( y_k -t_k \right)y_k(1-y_k)h_i\]

2. Siguiendo el método del gradiente descendente, actualizamos los pesos \(w^{2}_{ki}\) en esta capa. Llamando \(\textbf{w}^2=\left( w^2_{ki} \right)_{k=1,2;i=1,2,3}\) \[\textbf{w}^2 \leftarrow \textbf{w}^2 - \varepsilon \nabla_{\textbf{w}^2}L\]
3. Aplicamos la regla de la cadena en la capa oculta: \[\dfrac{\partial L}{\partial w^{1}_{ij}} \rightarrow \dfrac{\partial L}{\partial h_i}\dfrac{\partial h_i}{\partial a^{1}_i}\dfrac{\partial a^{1}_i}{\partial w^{1}_{ij}}\] con \((i=1,2,3)\):
   • \(\dfrac{\partial }{\partial w^{1}_{ij}}a^{1}_i(w^1_{i1},w^1_{i2})=x_j \quad (j=1,2)\)
   • \(\dfrac{\partial h_i}{\partial a^{1}_i}=\dfrac{\partial }{\partial a^{1}_i}\sigma (a_i^1)=\sigma(a^{1}_{i})(1-\sigma(a^{1}_{i}))=h_i(1-h_i)\)
   • Para calcular \(\dfrac{\partial L}{\partial h_i}\) tenemos en cuenta la dependencia de las funciones respecto a las distintas variables: \(L(y_1,y_2)\), \(y_k(a_k^2)\) y \(a_k^2(h_1,h_2,h_3)\). Así, aplicando la regla de la cadena: \[\dfrac{\partial L}{\partial h_{i}} \rightarrow \dfrac{\partial L}{\partial y_1}\dfrac{\partial y_1}{\partial a^{2}_1}\dfrac{\partial a^{2}_1}{\partial h_{i}} + \dfrac{\partial L}{\partial y_2}\dfrac{\partial y_2}{\partial a^{2}_2}\dfrac{\partial a^{2}_2}{\partial h_{i}}\] Ya habíamos obtenido anteriormente las expresiones para \(\dfrac{\partial L}{\partial y_k}\) y \(\dfrac{\partial y_k}{\partial a^{2}_k}\), por lo que sólo queda calcular el último factor de cada sumando:
     • \(\dfrac{\partial a^{k}_2}{\partial h_{i}}=w^{2}_{ki}\)

   Sustituyendo: \[\dfrac{\partial L}{\partial w^{1}_{ij}} \rightarrow x_jh_i(1-h_i)\sum^{2}_{k=1}\left[(y_k-t_k)y_k(1-y_k)w^{2}_{ki} \right]\]

4. Finalmente, se actualizan los pesos \(w^{1}_{ij}\). Llamando \(\textbf{w}^1=\left( w^1_{ij} \right)_{i=1,2,3:j=1,2}\) \[\textbf{w}^1 \leftarrow \textbf{w}^1 - \varepsilon \nabla_{\textbf{w}^1}L\]

Con esto se ha dado un paso de la iteración de la actualización de los pesos. A continuación, se volvería a repetir el proceso partiendo de los valores de los datos \(\bf{x}\).

En la práctica se suele contar para el entrenamiento con un conjunto de datos (no solo uno) y la función que se minimiza entonces es la suma de todas las “pérdidas” que se tienen al considerar todos esos datos.