2: Introducción al Cálculo Multivariante
( \newcommand{\kernel}{\mathrm{null}\,}\)
Presentamos inicialmente algunos conceptos como los de función multivariante, derivada parcial, gradiente, así como la composición de funciones de varias variables y la regla de la cadena para su derivación. Todos ellos serán imprescindibles en el desarrollo subsiguiente, en el que se introduce un algoritmo de aprendizaje supervisado muy utilizado para entrenar redes neuronales. Nos valdremos para ello del método del gradiente descendente, en cuya aplicación efectiva se emplea la estrategia de retropropagación, indicada para el cálculo del gradiente de funciones mediante la aplicación recursiva de la regla de la cadena.
Definición 1. Una función f:Rn→Rk lleva x∈Rn en y=f(x)∈Rk. Se dice que Rn es el dominio de f y para cada x∈Rn, el vector y=f(x) es la imagen de x por f. El conjunto de todas las imágenes se denomina también imagen de f.
- x=(x1,…,xn)T.
- f(x)=(f1(x),…,fk(x))T y cada fi(x) es una función coordenada de f.
- Si k=1, f(x)∈R.
Observación 2.1
Los vectores x∈Rn son vectores columna. Por comodidad, usamos la notación x=(x1,…,xn)T para indicar el traspuesto del vector fila (x1,…,xn). En ocasiones preferiremos la notación f(x,y), que resulta más simple que f((x,y)T).
Funciones Lineales
Para números reales fijos a1,a2,a3, la función lineal f de dominio R3 dada por f(x1,x2,x3)=a1x1+a2x2+a3x3 cumple que fijadas dos de las variables.
Por ejemplo x1=−3 y x2=5, la función g(x3)=−3a1+5a2+a3x3 es una función lineal.
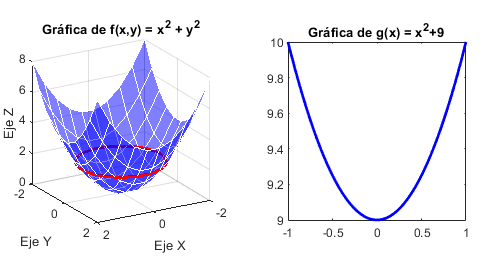
Consideramos la función f(x,y)=x2+y2, con dominio R2 e imagen en R. El valor mı́nimo que toma la función es 0, en el punto (0,0). En todos los puntos (x,y) que estén sobre la circunferencia centrada en (0,0) y radio r>0, la función f toma el valor r2. Si fijamos una de las variables, por ejemplo y=3, obtenemos la función g(x)=x2+9, cuya gráfica es una parábola. Podemos represintar la función f, que es la superficie de R3 de la gráfica siguiente:
Observación 2.2
Cuando trabajemos con una función f:Rn→R y fijemos n−1 variables, obtenemos una función con dominio e imagen en R, que podemos analizar con las técnicas ya conocidas.
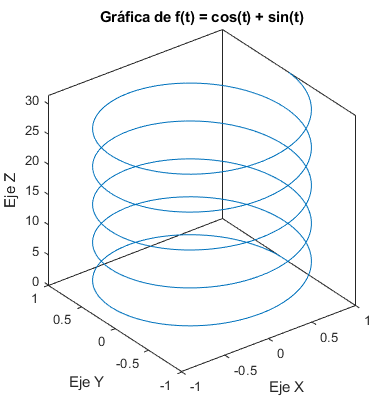
La función f:R→R2 dada por f(t)=(cos(t),sin(t)) viene definida por las funciones coordenadas f1(t)=cos(t) y f2(t)=sin(t). La gráfica de f es una hélice contenida en R3. La imagen de f es el conjunto C:={(x,y)∈R2:x2+y2=1}, ya que para todo t∈R se cumple que cos2(t)+sin2(t)=1 .
Nos encontraremos con la función sigmoide σ(x)=11+e−x, que es derivable y (¡Compruébalo!) su derivada es σ′(x)=σ(x)(1−σ(x))
Revisamos para una función f:R→R (es decir: n=k=1), la noción de derivada en un punto x.
La derivada de f en x, que notamos f′(x), viene dada (¡Cuando existe!) por: limh→0f(x+h)−f(x)h
Recuerda que f′(x) es la pendiente de la recta que más se asemeja a la gráfica de la función entre las que pasan por el punto (x,f(x)). Como la recta que une los puntos (a,b) y (c,d) tiene pendiente d−bc−a, la recta que une (x,f(x)) con (x+h,f(x+h)) tiene como pendiente f(x+h)−f(x)h, por lo que f′(x) es el lı́mite de las pendientes de estas rectas.
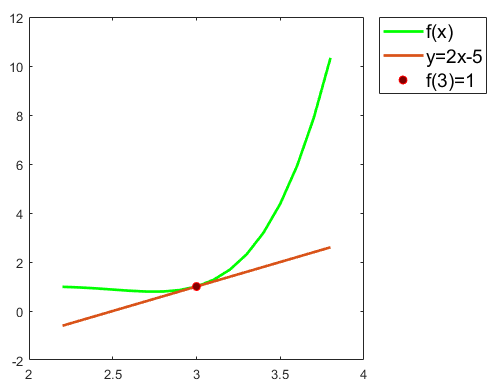
Si f:R→R cumple que f(3)=1 y f′(3)=2, el valor f(3) no puede ser mı́nimo (ni máximo), ya que la gráfica cerca de 3 es similar a la recta y=f(3)+f′(3)(x−3)=1+2(x−3); es decir, y=2x−5.
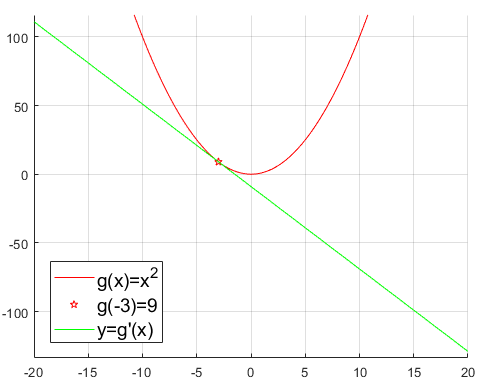
Si pensamos en la función g(x)=x2 y x=−3, como g′(−3)=−6, a la derecha de −3 la función tomará valores menores que g(−3)=9. El valor mı́nimo de la función, que es g(0)=0, se alcanza en un punto donde la derivada es nula.
La derivada parcial de la función f:Rn→R con respecto a la variable xj en x=(x1,…,xj−1,xj,xj+1,…,xn)T, que denotamos ∂∂xjf(x), viene dada por limh→0f(x1,…,xj−1,xj+h,xj+1,…,xn)−f(x1,⋯,xj−1,xj,xj+1,…,xn)h
La función f(x,y)=x2+y2 tiene como derivadas parciales ∂∂xf(x,y)=2x y ∂∂yf(x,y)=2y. La función f(x1,x2,x3)=a1x1+a2x2+a3x3 tiene como derivada parcial con respecto a xj el número aj, para 1≤j≤3. La función f(x,y)=sin(xy3)+x2y tiene como derivadas parciales ∂∂xf(x,y)=y3⋅cos(xy3)+2xy y ∂∂yf(x,y)=3xy2cos(xy3)+x2.
Dada una función f:Rn→R con derivadas parciales ∂∂xjf(x), el gradiente de f se denota por ∇f(x) y tiene por coordenadas las funciones ∂∂xjf(x), con 1≤j≤n.
La función f(x,y)=x2+y2 tiene como gradiente la función ∇f(x,y)=(2x,2y)T. La función f(x1,x2,x3)=a1x1+a2x2+a3x3 tiene como gradiente el vector constante ∇f(x)=(a1,a2,a3)T.
Observación 2.3
Como veremos más adelante, el hecho de que la dirección del gradiente ∇f(x) sea la de máximo crecimiento de la función f en cada punto x y la dirección dada por su opuesto, −∇f(x), la de mayor decrecimiento, permite establecer una estrategia para minimizar la función escalar f(x). Para la función f(x,y)=x2+y2 en el punto (−3,4) hemos elegido valores (h1,h2) de signos opuestos al gradiente (−6,8) para obtener puntos (−3+h1,4+h2) en los que f toma valores menores que f(−3,4)=25.
Si trabajamos con una función f:Rn→Rk de k coordenadas f1,f2,…,fk, cuando existan las n derivadas parciales de cada una de ellas podemos considerar la función matricial de k filas y n columnas formada por los k gradientes ∇fk. Se trata de la matriz jacobiana de la función f.
