2.5E: Ejercicios para la Sección 2.5

Última actualización
Guardar como PDF

Page ID: 116887

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

En los ejercicios 1 - 4, escribir la$ ε − δ$ definición apropiada para cada una de las declaraciones dadas.

1)$\displaystyle \lim_{x →a}f(x)=N$

2)$\displaystyle \lim_{t →b}g(t)=M$

Contestar: Por cada$ ε >0$, existe una$ δ >0$, de modo que si$0 <|t −b| < δ$, entonces$|g(t) −M| < ε$

3)$\displaystyle \lim_{x →c}h(x)=L$

4)$\displaystyle \lim_{x →a} φ(x)=A$

Contestar: Por cada$ ε >0$, existe una$ δ >0$, de modo que si$0 <|x −a| < δ$, entonces$| φ(x) −A| < ε$

La siguiente gráfica de la función$f$ satisface$\displaystyle \lim_{x →2}f(x)=2$. En los siguientes ejercicios, determinar un valor de$ δ >0$ que satisfaga cada enunciado.

Una función dibujada en el cuadrante uno para x 0. Es una función ascendente cóncava creciente, con puntos aproximadamente (0,0), (1, .5), (2,2) y (3,4)." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_204.jpeg">

5) Si$0 <|x −2| < δ$, entonces$|f(x) −2| <1$.

6) Si$0 <|x −2| < δ$, entonces$|f(x) −2| <0.5$.

Contestar: $ δ ≤0.25$

La siguiente gráfica de la función$f$ satisface$\displaystyle \lim_{x →3}f(x)= −1$. En los siguientes ejercicios, determinar un valor de$ δ >0$ que satisfaga cada enunciado.

Una gráfica de una función lineal decreciente, con puntos (0,2), (1,1), (2,0), (3, -1), (4, -2), y así sucesivamente para x = 0." style="width: 417px; height: 422px;" width="417px" height="422px" src="https://math.libretexts.org/@api/dek...02_05_205.jpeg">

7) Si$0 <|x −3| < δ$, entonces$|f(x)+1| <1$.

8) Si$0 <|x −3| < δ$, entonces$|f(x)+1| <2$.

Contestar: $ δ ≤2$

La siguiente gráfica de la función$f$ satisface$\displaystyle \lim_{x →3}f(x)=2$. En los siguientes ejercicios, por cada valor de$ ε$, encontrar un valor de$ δ >0$ tal manera que la definición precisa de límite sea cierta.

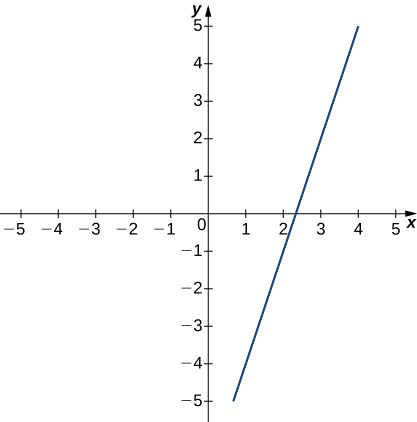
$Una gráfica de una función lineal creciente que interseca el eje x aproximadamente (2.25, 0) y recorriendo los puntos (3,2) y, aproximadamente, (1, -5) y (4,5).$

9)$ ε=1.5$

10)$ ε=3$

Contestar: $ δ ≤1$

[T] En los ejercicios 11 a 12, usa una calculadora gráfica para encontrar un número$ δ$ tal que las afirmaciones sean verdaderas.

11)$\left|\sin(2x) −\frac{1}{2}\right| <0.1$, siempre que$\left|x −\frac{ π}{12}\right| < δ$

12)$\left|\sqrt{x −4} −2\right| <0.1$, siempre que$|x −8| < δ$

Contestar: $ δ <0.3900$

En los ejercicios 13 - 17, utilizar la definición precisa de límite para probar los límites dados.

13)$\displaystyle \lim_{x →2}\,(5x+8)=18$

14)$\displaystyle \lim_{x →3}\frac{x^2 −9}{x −3}=6$

Contestar: Vamos$ δ= ε$. Si$0 <|x −3| < ε$, entonces$\left|\dfrac{x^2 −9}{x −3} - 6\right| = \left|\dfrac{(x+3)(x −3)}{x −3} - 6\right| = |x+3 −6|=|x −3| < ε$.

15)$\displaystyle \lim_{x →2}\frac{2x^2 −3x −2}{x −2}=5$

16)$\displaystyle \lim_{x →0}x^4=0$

Contestar: Vamos$ δ=\sqrt[4]{ ε}$. Si$0 <|x| <\sqrt[4]{ ε}$, entonces$\left|x^4-0\right|=x^4 < ε$.

17)$\displaystyle \lim_{x →2}\,(x^2+2x)=8$

En los ejercicios 18 - 20, utilice la definición precisa de límite para probar los límites unilaterales dados.

18)$\displaystyle \lim_{x →5^ −}\sqrt{5 −x}=0$

Contestar: Vamos$ δ= ε^2$. Si$- ε^2 < x - 5 < 0,$ podemos multiplicar por$-1$ para obtener$0 <5-x < ε^2.$
Entonces$\left|\sqrt{5 −x} - 0\right|=\sqrt{5 −x} < \sqrt{ ε^2} = ε$.

19)$\displaystyle \lim_{x →0^+}f(x)= −2$, donde$f(x)=\begin{cases}8x −3, & \text{if }x <0\\4x −2, & \text{if }x ≥0\end{cases}$.

20)$\displaystyle \lim_{x →1^ −}f(x)=3$, donde$f(x)=\begin{cases}5x −2, & \text{if }x <1\\7x −1, & \text{if }x ≥1\end{cases}$.

Contestar: Vamos$ δ= ε/5$. Si$ − ε/5 < x - 1 <0,$ podemos multiplicar por$-1$ para llegar$0 <1-x < ε/5.$
Entonces$|f(x) −3|=|5x-2-3| = |5x −5| = 5(1-x),$ desde$x <1$ aquí.
Y$5(1-x) < 5( ε/5) = ε$.

En los ejercicios 21 - 23, utilizar la definición precisa de límite para probar los límites infinitos dados.

21)$\displaystyle \lim_{x →0}\frac{1}{x^2}= ∞$

22)$\displaystyle \lim_{x → −1}\frac{3}{(x+1)^2}= ∞$

Contestar: Vamos$ δ=\sqrt{\frac{3}{N}}$. Si$0 <|x+1| <\sqrt{\frac{3}{N}}$, entonces$f(x)=\frac{3}{(x+1)^2} >N$.

23)$\displaystyle \lim_{x →2} −\frac{1}{(x −2)^2}= − ∞$

24) Un ingeniero está utilizando una máquina para cortar un cuadrado plano de Aerogel de área$144 \,\text{cm}^2$. Si hay una tolerancia máxima a errores en el área de$8 \,\text{cm}^2$, ¿con qué precisión debe cortar el ingeniero en el costado, asumiendo que todos los lados tienen la misma longitud? ¿Cómo se relacionan estos números con$ δ$$ ε$,$a$, y$L$?

Contestar: $0.033 \text{ cm}, \, ε=8,\, δ=0.33,\,a=12,\,L=144$

25) Utilizar la definición precisa de límite para demostrar que no existe el siguiente límite:$\displaystyle \lim_{x →1}\frac{|x −1|}{x −1}.$

26) Utilizando definiciones precisas de límites, demostrar que$\displaystyle \lim_{x →0}f(x)$ no existe, dado que$f(x)$ es la función de techo. (Pista: Prueba cualquiera$ δ <1$.)

Contestar: Las respuestas pueden muy.

27) Utilizando definiciones precisas de límites, demostrar que$\displaystyle \lim_{x →0}f(x)$ no existe:$f(x)=\begin{cases}1, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Pista: Piensa en cómo puedes elegir siempre un número racional$0 <d$, >

28) Utilizando definiciones precisas de límites, determinar$\displaystyle \lim_{x →0}f(x)$ para$f(x)=\begin{cases}x, & \text{if }x\text{ is rational}\\0, & \text{if }x\text{ is irrational}\end{cases}$. (Pista: Romper en dos casos,$x$ racional e$x$ irracional.)

Contestar: $0$

29) Utilizando la función del ejercicio anterior, utilizar la definición precisa de límites para demostrar que$\displaystyle \lim_{x →a}f(x)$ no existe para$a ≠0$

Para los ejercicios 30 - 32, supongamos que$\displaystyle \lim_{x →a}f(x)=L$ y$\displaystyle \lim_{x →a}g(x)=M$ ambos existen. Utilice la definición precisa de límites para probar las siguientes leyes de límites:

30)$\displaystyle \lim_{x →a}(f(x) −g(x))=L −M$

Contestar: $f(x) −g(x)=f(x)+( −1)g(x)$

31)$\displaystyle \lim_{x →a}[cf(x)]=cL$ para cualquier constante real$c$ (Pista: Considere dos casos:$c=0$ y$c ≠0$.)

32)$\displaystyle \lim_{x →a}[f(x)g(x)]=LM$. (Pista:$|f(x)g(x) −LM|= |f(x)g(x) −f(x)M +f(x)M −LM| ≤|f(x)||g(x) −M| +|M||f(x) −L|.)$

Contestar: Las respuestas pueden variar.

Search

Text Color

Text Size

Margin Size

Font Type