3.7: Derivadas de funciones inversas
- Page ID
- 116583
- Calcular la derivada de una función inversa.
- Reconocer las derivadas de las funciones trigonométricas inversas estándar.
En esta sección exploramos la relación entre la derivada de una función y la derivada de su inversa. Para funciones cuyas derivadas ya conocemos, podemos usar esta relación para encontrar derivadas de inversos sin tener que usar la definición límite de la derivada. En particular, aplicaremos la fórmula para derivadas de funciones inversas a funciones trigonométricas. Esta fórmula también se puede utilizar para extender la regla de poder a exponentes racionales.
La derivada de una función inversa
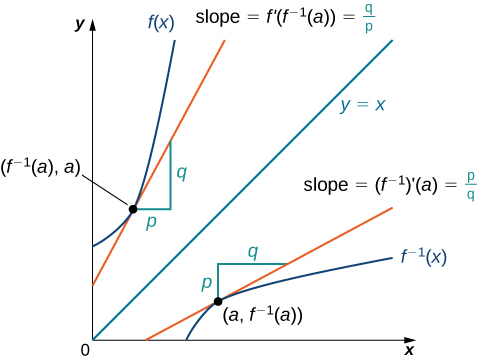
Comenzamos por considerar una función y su inversa. Si\(f(x)\) es tanto invertible como diferenciable, parece razonable que la inversa de también\(f(x)\) sea diferenciable. La figura\(\PageIndex{1}\) muestra la relación entre una función\(f(x)\) y su inversa\(f^{−1}(x)\). Mira el punto\(\left(a,\,f^{−1}(a)\right)\) en la gráfica de\(f^{−1}(x)\) tener una línea tangente con una pendiente de
\[\big(f^{−1}\big)′(a)=\dfrac{p}{q}. \nonumber \]
Este punto corresponde a un punto\(\left(f^{−1}(a),\,a\right)\) en la gráfica de\(f(x)\) tener una línea tangente con una pendiente de
\[f′\big(f^{−1}(a)\big)=\dfrac{q}{p}. \nonumber \]
Así, si\(f^{−1}(x)\) es diferenciable en\(a\), entonces debe darse el caso de que
\(\big(f^{−1}\big)′(a)=\dfrac{1}{f′\big(f^{−1}(a)\big)}\).
También podemos derivar la fórmula para la derivada de la inversa recordando primero eso\(x=f\big(f^{−1}(x)\big)\). Luego, diferenciando ambos lados de esta ecuación (usando la regla de la cadena a la derecha), obtenemos
\(1=f′\big(f^{−1}(x)\big)\big(f^{−1}\big)′(x))\).
Resolviendo para\(\big(f^{−1}\big)′(x)\), obtenemos
\(\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\).
Resumimos este resultado en el siguiente teorema.
Dejar\(f(x)\) ser una función que sea a la vez invertible y diferenciable. Dejar\(y=f^{−1}(x)\) ser la inversa de\(f(x)\). Para todos\(x\) satisfactorios\(f′\big(f^{−1}(x)\big)≠0\),
\[\dfrac{dy}{dx}=\dfrac{d}{dx}\big(f^{−1}(x)\big)=\big(f^{−1}\big)′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}.\label{inverse1} \]
Alternativamente, si\(y=g(x)\) es la inversa de\(f(x)\), entonces
\[g'(x)=\dfrac{1}{f′\big(g(x)\big)}. \label{inverse2} \]
Utilice el teorema de la función inversa para encontrar la derivada de\(g(x)=\dfrac{x+2}{x}\). Comparar la derivada resultante con la obtenida diferenciando la función directamente.
Solución
La inversa de\(g(x)=\dfrac{x+2}{x}\) es\(f(x)=\dfrac{2}{x−1}\).
Usaremos la ecuación\ ref {inverse2} y comenzaremos por encontrar\(f′(x)\). Por lo tanto,
\[f′(x)=\dfrac{−2}{(x−1)^2} \nonumber \]
y
\[f′\big(g(x)\big)=\dfrac{−2}{(g(x)−1)^2}=\dfrac{−2}{\left(\dfrac{x+2}{x}−1\right)^2}=−\dfrac{x^2}{2}. \nonumber \]
Por último,
\[g′(x)=\dfrac{1}{f′\big(g(x)\big)}=−\dfrac{2}{x^2}. \nonumber \]
Podemos verificar que esta es la derivada correcta aplicando la regla del cociente\(g(x)\) para obtener
\[g′(x)=−\dfrac{2}{x^2}. \nonumber \]
Utilice el teorema de la función inversa para encontrar la derivada de\(g(x)=\dfrac{1}{x+2}\). Comparar el resultado obtenido diferenciando\(g(x)\) directamente.
- Pista
-
Utilice el ejemplo anterior como guía.
- Responder
-
\(g′(x)=−\dfrac{1}{(x+2)^2}\)
Utilice el teorema de la función inversa para encontrar la derivada de\(g(x)=\sqrt[3]{x}\).
Solución
La función\(g(x)=\sqrt[3]{x}\) es la inversa de la función\(f(x)=x^3\). Ya que\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), comenzar por encontrar\(f′(x)\). Por lo tanto,
\[f′(x)=3x^2\nonumber \]
y
\[f′\big(g(x)\big)=3\big(\sqrt[3]{x}\big)^2=3x^{2/3}\nonumber \]
Por último,
\[g′(x)=\dfrac{1}{3x^{2/3}}.\nonumber \]
Si tuviéramos que diferenciarnos\(g(x)\) directamente, usando la regla de poder, primero reescribiríamos\(g(x)=\sqrt[3]{x}\) como un poder de\(x\) para obtener,
\[g(x) = x^{1/3}\nonumber \]
Entonces diferenciaríamos usando la regla de poder para obtener
\[g'(x) =\tfrac{1}{3}x^{−2/3} = \dfrac{1}{3x^{2/3}}.\nonumber \]
Encontrar la derivada de\(g(x)=\sqrt[5]{x}\) aplicando el teorema de la función inversa.
- Pista
-
\(g(x)\)es la inversa de\(f(x)=x^5\).
- Responder
-
\(g(x)=\frac{1}{5}x^{−4/5}\)
Del ejemplo anterior, vemos que podemos usar el teorema de la función inversa para extender la regla de potencia a exponentes de la forma\(\dfrac{1}{n}\), donde\(n\) es un entero positivo. Esta extensión en última instancia nos permitirá diferenciar\(x^q\), donde\(q\) está cualquier número racional.
La regla de poder puede extenderse a exponentes racionales. Es decir, si\(n\) es un entero positivo, entonces
\[\dfrac{d}{dx}\big(x^{1/n}\big)=\dfrac{1}{n} x^{(1/n)−1}. \nonumber \]
Además, si\(n\) es un entero positivo y\(m\) es un entero arbitrario, entonces
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
La función\(g(x)=x^{1/n}\) es la inversa de la función\(f(x)=x^n\). Ya que\(g′(x)=\dfrac{1}{f′\big(g(x)\big)}\), comenzar por encontrar\(f′(x)\). Por lo tanto,
\(f′(x)=nx^{n−1}\)y\(f′\big(g(x)\big)=n\big(x^{1/n}\big)^{n−1}=nx^{(n−1)/n}\).
Por último,
\(g′(x)=\dfrac{1}{nx^{(n−1)/n}}=\dfrac{1}{n}x^{(1−n)/n}=\dfrac{1}{n}x^{(1/n)−1}\).
Para diferenciarlo\(x^{m/n}\) debemos reescribirlo como\((x^{1/n})^m\) y aplicar la regla de la cadena. Por lo tanto,
\[\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{d}{dx}\big((x^{1/n}\big)^m)=m\big(x^{1/n}\big)^{m−1}⋅\dfrac{1}{n}x^{(1/n)−1}=\dfrac{m}{n}x^{(m/n)−1}. \nonumber \]
□
Encuentra la ecuación de la línea tangente a la gráfica de\(y=x^{2/3}\) at\(x=8\).
Solución
Primero\(\dfrac{dy}{dx}\) encuéntralo y evalúalo en\(x=8\). Desde
\[\dfrac{dy}{dx}=\frac{2}{3}x^{−1/3} \nonumber \]
y
\[\dfrac{dy}{dx}\Bigg|_{x=8}=\frac{1}{3}\nonumber \]
la pendiente de la línea tangente a la gráfica en\(x=8\) es\(\frac{1}{3}\).
Sustituyendo\(x=8\) a la función original, obtenemos\(y=4\). Así, la línea tangente pasa por el punto\((8,4)\). Sustituyendo en la fórmula de punto-pendiente por una línea, obtenemos la línea tangente
\[y=\tfrac{1}{3}x+\tfrac{4}{3}. \nonumber \]
Encuentra la derivada de\(s(t)=\sqrt{2t+1}\).
- Pista
-
Usa la regla de la cadena.
- Responder
-
\(s′(t)=(2t+1)^{−1/2}\)
Derivadas de funciones trigonométricas inversas
Ahora volvemos nuestra atención hacia la búsqueda de derivadas de funciones trigonométricas inversas. Estos derivados resultarán invaluables en el estudio de la integración más adelante en este texto. Las derivadas de las funciones trigonométricas inversas son bastante sorprendentes ya que sus derivadas son en realidad funciones algebraicas. Anteriormente, las derivadas de funciones algebraicas han demostrado ser funciones algebraicas y las derivadas de funciones trigonométricas han demostrado ser funciones trigonométricas. Aquí, por primera vez, vemos que la derivada de una función no necesita ser del mismo tipo que la función original.
Utilice el teorema de la función inversa para encontrar la derivada de\(g(x)=\sin^{−1}x\).
Solución
Ya que para\(x\) en el intervalo\(\left[−\frac{π}{2},\frac{π}{2}\right],f(x)=\sin x\) es la inversa de\(g(x)=\sin^{−1}x\), comenzar por encontrar\(f′(x)\). Desde
\[f′(x)=\cos x \nonumber \]
y
\[f′\big(g(x)\big)=\cos \big( \sin^{−1}x\big)=\sqrt{1−x^2} \nonumber \]
vemos que
\[g′(x)=\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{f′\big(g(x)\big)}=\dfrac{1}{\sqrt{1−x^2}} \nonumber \]
Análisis
Para verlo\(\cos(\sin^{−1}x)=\sqrt{1−x^2}\), considere el siguiente argumento. Set\(\sin^{−1}x=θ\). En este caso,\(\sin θ=x\) donde\(−\frac{π}{2}≤θ≤\frac{π}{2}\). Empezamos por considerar el caso donde\(0<θ<\frac{π}{2}\). Dado que\(θ\) es un ángulo agudo, podemos construir un triángulo rectángulo con ángulo agudo\(θ\), una hipotenusa de longitud\(1\) y el lado opuesto el ángulo\(θ\) que tiene longitud\(x\). Del teorema de Pitágoras, el lado adyacente al ángulo\(θ\) tiene longitud\(\sqrt{1−x^2}\). Este triángulo se muestra en la Figura\(\PageIndex{2}\) Usando el triángulo, vemos eso\(\cos(\sin^{−1}x)=\cos θ=\sqrt{1−x^2}\).
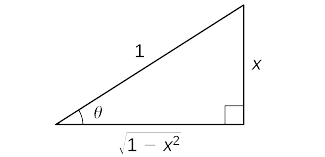
En el caso donde\(−\frac{π}{2}<θ<0\), hacemos la observación de que\(0<−θ<\frac{π}{2}\) y por lo tanto
\(\cos\big(\sin^{−1}x\big)=\cos θ=\cos(−θ)=\sqrt{1−x^2}\).
Ahora si\(θ=\frac{π}{2}\) o\(θ=−\frac{π}{2},x=1\) o\(x=−1\), y ya que en cualquiera de\(\cosθ=0\) los casos y\(\sqrt{1−x^2}=0\), tenemos
\(\cos\big(\sin^{−1}x\big)=\cosθ=\sqrt{1−x^2}\).
En consecuencia, en todos los casos,
\[\cos\big(\sin^{−1}x\big)=\sqrt{1−x^2}.\nonumber \]
Aplicar la regla de la cadena a la fórmula derivada en Ejemplo\(\PageIndex{4A}\) para encontrar la derivada de\(h(x)=\sin^{−1}\big(g(x)\big)\) y utilizar este resultado para encontrar la derivada de\(h(x)=\sin^{−1}(2x^3).\)
Solución
Aplicando la regla de la cadena a\(h(x)=\sin^{−1}\big(g(x)\big)\), tenemos
\(h′(x)=\dfrac{1}{\sqrt{1−\big(g(x)\big)^2}}g′(x)\).
Ahora déjalo\(g(x)=2x^3,\) así\(g′(x)=6x^2\). Sustituyendo al resultado anterior, obtenemos
\(\begin{align*} h′(x)&=\dfrac{1}{\sqrt{1−4x^6}}⋅6x^2\\[4pt]&=\dfrac{6x^2}{\sqrt{1−4x^6}}\end{align*}\)
Utilice el teorema de la función inversa para encontrar la derivada de\(g(x)=\tan^{−1}x\).
- Pista
-
La inversa de\(g(x)\) es\(f(x)=\tan x\). Use Ejemplo\(\PageIndex{4A}\) como guía.
- Responder
-
\(g′(x)=\dfrac{1}{1+x^2}\)
Las derivadas de las funciones trigonométricas inversas restantes también se pueden encontrar usando el teorema de la función inversa. Estas fórmulas se proporcionan en el siguiente teorema.
\[\begin{align} \dfrac{d}{dx}\big(\sin^{−1}x\big) &=\dfrac{1}{\sqrt{1−x^2}} \label{trig1} \\[4pt] \dfrac{d}{dx}\big(\cos^{−1}x\big) &=\dfrac{−1}{\sqrt{1−x^2}} \label{trig2} \\[4pt] \dfrac{d}{dx}\big(\tan^{−1}x\big) &=\dfrac{1}{1+x^2} \label{trig3} \\[4pt] \dfrac{d}{dx}\big(\cot^{−1}x\big) &=\dfrac{−1}{1+x^2} \label{trig4} \\[4pt] \dfrac{d}{dx}\big(\sec^{−1}x\big) &=\dfrac{1}{|x|\sqrt{x^2−1}} \label{trig5} \\[4pt] \dfrac{d}{dx}\big(\csc^{−1}x\big) &=\dfrac{−1}{|x|\sqrt{x^2−1}} \label{trig6} \end{align} \]
Encuentra la derivada de\(f(x)=\tan^{−1}(x^2).\)
Solución
Vamos\(g(x)=x^2\), entonces\(g′(x)=2x\). Sustituyendo en la Ecuación\ ref {trig3}, obtenemos
\(f′(x)=\dfrac{1}{1+(x^2)^2}⋅(2x).\)
Simplificando, tenemos
\(f′(x)=\dfrac{2x}{1+x^4}\).
Encuentra la derivada de\(h(x)=x^2 \sin^{−1}x.\)
Solución
Al aplicar la regla del producto, tenemos
\(h′(x)=2x\sin^{−1}x+\dfrac{1}{\sqrt{1−x^2}}⋅x^2\)
Encuentra la derivada de\(h(x)=\cos^{−1}(3x−1).\)
- Pista
-
Utilice la ecuación\ ref {trig2}. con\(g(x)=3x−1\)
- Responder
-
\(h′(x)=\dfrac{−3}{\sqrt{6x−9x^2}}\)
La posición de una partícula en el momento\(t\) viene dada por\(s(t)=\tan^{−1}\left(\frac{1}{t}\right)\) for\(t≥ \ce{1/2}\). Encuentra la velocidad de la partícula a la vez\( t=1\).
Solución
Empezar por diferenciar\(s(t)\) para encontrar\(v(t)\) .Así,
\(v(t)=s′(t)=\dfrac{1}{1+\left(\frac{1}{t}\right)^2}⋅\dfrac{−1}{t^2}\).
Simplificando, tenemos
\(v(t)=−\dfrac{1}{t^2+1}\).
Así,\(v(1)=−\dfrac{1}{2}.\)
Encuentra la ecuación de la línea tangente a la gráfica de\(f(x)=\sin^{−1}x\) at\(x=0.\)
- Pista
-
\(f′(0)\)es la pendiente de la línea tangente.
- Responder
-
\(y=x\)
Conceptos clave
- El teorema de la función inversa nos permite calcular derivadas de funciones inversas sin usar la definición límite de la derivada.
- Podemos utilizar el teorema de la función inversa para desarrollar fórmulas de diferenciación para las funciones trigonométricas inversas.
Ecuaciones Clave
- Teorema de función inversa
\((f^{−1})′(x)=\dfrac{1}{f′\big(f^{−1}(x)\big)}\)siempre\(f′\big(f^{−1}(x)\big)≠0\) y\(f(x)\) sea diferenciable.
- Regla de potencia con exponentes racionales
\(\dfrac{d}{dx}\big(x^{m/n}\big)=\dfrac{m}{n}x^{(m/n)−1}.\)
- Derivada de la función sinusoidal inversa
\(\dfrac{d}{dx}\big(\sin^{−1}x\big)=\dfrac{1}{\sqrt{1−x^2}}\)
- Derivada de la función coseno inversa
\(\dfrac{d}{dx}\big(\cos^{−1}x\big)=\dfrac{−1}{\sqrt{1−x^2}}\)
Derivada de la función tangente inversa
\(\dfrac{d}{dx}\big(\tan^{−1}x\big)=\dfrac{1}{1+x^2}\)
Derivada de la función cotangente inversa
\(\dfrac{d}{dx}\big(\cot^{−1}x\big)=\dfrac{−1}{1+x^2}\)
Derivada de la función secante inversa
\(\dfrac{d}{dx}\big(\sec^{−1}x\big)=\dfrac{1}{|x|\sqrt{x^2−1}}\)
Derivada de la función cosecante inversa
\(\dfrac{d}{dx}\big(\csc^{−1}x\big)=\dfrac{−1}{|x|\sqrt{x^2−1}}\)
Colaboradores y Atribuciones
- Template:ContribOpenStaxCalc
- Paul Seeburger (Monroe Community College) added the second half of Example \(\PageIndex{2}\).