4.11: Capítulo 4 Ejercicios de revisión

Última actualización
Guardar como PDF

Page ID: 116385

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

¿Verdadero o Falso? Justifica tu respuesta con una prueba o un contraejemplo. Supongamos que$f(x)$ es continuo y diferenciable a menos que se indique lo contrario.

1) Si$f(−1)=−6$ y$f(1)=2$, entonces existe al menos un punto$x∈[−1,1]$ tal que$f′(x)=4.$

Contestar: Verdadero, por Teorema del Valor Medio

2) Si$f′(c)=0,$ hay un máximo o mínimo en$x=c.$

3) Hay una función tal que$f(x)<0,f′(x)>0,$ y$f''(x)<0.$ (Una “prueba” gráfica es aceptable para esta respuesta.)

Contestar: Cierto

4) Hay una función tal que hay tanto un punto de inflexión como un punto crítico para algún valor$x=a.$

5) Dada la gráfica de$f′$, determinar dónde$f$ está aumentando o disminuyendo.

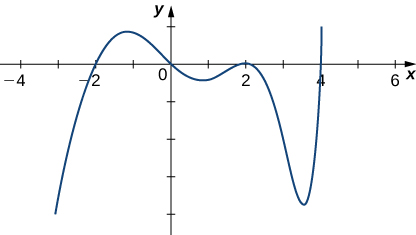
$La función aumenta para cruzar el eje x en −2, alcanza un máximo y luego disminuye a través del origen, alcanza un mínimo y luego aumenta a un máximo en 2, disminuye a un mínimo y luego aumenta para pasar por el eje x a 4 y continúa aumentando.$

Contestar: Incrementando:$(−2,0)∪(4,∞)$, decreciente:$(−∞,−2)∪(0,4)$

6) La gráfica de$f$ se da a continuación. Empate$f′$.

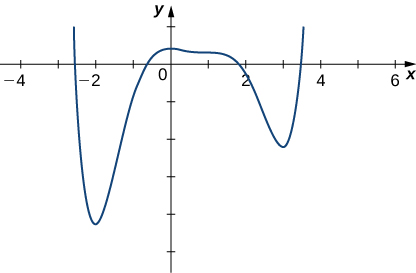
$La función disminuye rápidamente y alcanza un mínimo local en −2, luego aumenta hasta alcanzar un máximo local en 0, momento en el que disminuye lentamente al principio, luego deja de disminuir cerca de 1, luego continúa disminuyendo hasta alcanzar un mínimo en 3, y luego aumenta rápidamente.$

7) Encuentra la aproximación lineal$L(x)$ a$y=x^2+\tan(πx)$ cerca$x=\frac{1}{4}.$

Contestar: $L(x)=\frac{17}{16}+\frac{1}{2}(1+4π)\left(x−\frac{1}{4}\right)$

8) Encontrar el diferencial de$y=x^2−5x−6$ y evaluar$x=2$ con$dx=0.1.$

Encuentra los puntos críticos y los extremos locales y absolutos de las siguientes funciones en el intervalo dado.

9)$f(x)=x+\sin^2(x)$ sobre$[0,π]$

Contestar: Punto crítico: Mínimo$x=\frac{3π}{4},$
absoluto:$0$ cuando Máximo$x=0,$
absoluto:$π$ cuando$x=π$

Solución:

10)$f(x)=3x^4−4x^3−12x^2+6$ sobre$[−3,3]$

Determine en qué intervalos las siguientes funciones están aumentando, disminuyendo, cóncavas hacia arriba y cóncavas hacia abajo.

11)$x(t)=3t^4−8t^3−18t^2$

Contestar: Creciente:$(−1,0)∪(3,∞),$
Disminución:$(−∞,−1)∪(0,3),$
Cóncava hacia arriba:$\left(−∞,\frac{1}{3}\left(2−\sqrt{13}\right)\right)∪\left(\frac{1}{3}\left(2+\sqrt{13}\right),∞\right)$,
Cóncava$\left(\frac{1}{3}\left(2−\sqrt{13}\right),\frac{1}{3}\left(2+\sqrt{13}\right)\right)$

12)$y=x+\sin(πx)$

13)$g(x)=x−\sqrt{x}$

Contestar: Creciente:$\left(\frac{1}{4},∞\right),$
Disminución:$\left(0,\frac{1}{4}\right)$,
Cóncavo arriba:$(0,∞),$
Cóncavo

14)$f(θ)=\sin(3θ)$

Evaluar los siguientes límites.

15)$\displaystyle \lim_{x→∞}\frac{3x\sqrt{x^2+1}}{\sqrt{x^4−1}}$

Contestar: $3$

16)$\displaystyle \lim_{x→∞}\cos\left(\frac{1}{x}\right)$

17)$\displaystyle \lim_{x→1}\frac{x−1}{\sin(πx)}$

Contestar: $−\frac{1}{π}$

18)$\displaystyle \lim_{x→∞}(3x)^{1/x}$

Usa el método de Newton para encontrar las dos primeras iteraciones, dado el punto de partida.

19)$y=x^3+1,\quad x_0=0.5$

Contestar: $x_1=−1,\; x_2=−1$

20)$\dfrac{1}{x+1}=\dfrac{1}{2}, \quad x_0=0$

Encuentra los antiderivados$F(x)$ de las siguientes funciones.

21)$g(x)=\sqrt{x}−\dfrac{1}{x^2}$

Contestar: $F(x)=\dfrac{2x^{3/2}}{3}+\dfrac{1}{x}+C$

22)$f(x)=2x+6\cos x,\quad F(π)=π^2+2$

Grafica las siguientes funciones a mano. Asegúrese de etiquetar los puntos de inflexión, puntos críticos, ceros y asíntotas.

23)$y=\dfrac{1}{x(x+1)^2}$

Contestar

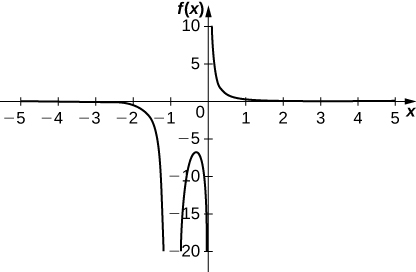
$Esta gráfica tiene asíntotas verticales en x = 0 y x = −1. La primera parte de la función ocurre en el tercer cuadrante con una asíntota horizontal en y = 0. La función disminuye rápidamente de cerca (−5, 0) a cerca de la asíntota vertical (−1, ∞). Al otro lado de la asíntota, la función tiene aproximadamente forma de U y apunta hacia abajo en el tercer cuadrante entre x = −1 y x = 0 con máximo cercano (−0.4, −6). Al otro lado de la asipotota x = 0, la función disminuye desde su asíntota vertical cerca (0, ∞) y para acercarse a la asíntota horizontal y = 0.$

Puntos de inflexión: ninguno; Puntos
críticos:$x=−\frac{1}{3}$;
Ceros: ninguno; asíntotas
verticales:$x=−1, \; x=0$; Asintota
horizontal:$y=0$

24)$y=x−\sqrt{4−x^2}$

25) Un automóvil está siendo compactado en un sólido rectangular. El volumen está disminuyendo a una tasa de$2\, \text{m}^3/\text{sec}$. El largo y ancho del compactador son cuadrados, pero la altura no es la misma longitud que el largo y ancho. Si las paredes de longitud y anchura se mueven una hacia la otra a una velocidad de$0.25$ m/seg, encuentre la velocidad a la que la altura está cambiando cuando la longitud y la anchura son$2$ m y la altura es$1.5$ m.

Contestar: La altura disminuye a una velocidad de$0.125$ m/seg

26) Un cohete es lanzado al espacio; su energía cinética viene dada por$K(t)=\frac{1}{2}m(t)v(t)^2$, donde$K$ está la energía cinética en julios,$m$ es la masa del cohete en kilogramos, y$v$ es la velocidad del cohete en metros/segundo. Supongamos que la velocidad está aumentando a una velocidad de$15 \,\text{m/sec}^2$ y la masa disminuye a una velocidad de$10$ kg/seg debido a que el combustible se está quemando. ¿A qué velocidad cambia la energía cinética del cohete cuando la masa es$2000$ kg y la velocidad es$5000$ m/seg? Da tu respuesta en Mega-julios (MJ), que equivale a$10^6$ J.

27) El famoso problema del regiomontano para la maximización angular se propuso durante el$15^\text{th}$ siglo. Una pintura cuelga de una pared con la parte inferior de la pintura a una distancia$a$ pies por encima del nivel de los ojos, y los$b$ pies superiores por encima del nivel de los ojos. ¿Qué distancia$x$ (en pies) de la pared debe pararse el espectador para maximizar el ángulo subtendido por la pintura,$θ$?

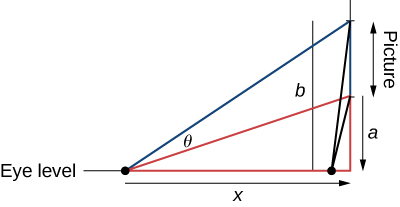
$Un punto se marca al nivel del ojo, y a partir de este punto se hace un triángulo rectángulo con la longitud del lado adyacente x y la longitud del lado opuesto a, que es la longitud desde la parte inferior de la imagen hasta el nivel del ojo. Un segundo triángulo rectángulo se realiza desde el punto marcado al nivel del ojo, siendo el lado adyacente x y el otro lado siendo la longitud b, que es la altura de la imagen. El ángulo entre las dos hipotenusas está marcado θ.$

Contestar: $x=\sqrt{ab}$pies

28) Una aerolínea vende boletos de Tokio a Detroit por$$1200.$ Hay$500$ asientos disponibles y un vuelo típico libro$350$ asientos. Por cada$$10$ disminución de precio, la aerolínea observa cinco asientos adicionales vendidos. ¿Cuál debería ser la tarifa para maximizar las ganancias? ¿Cuántos pasajeros estarían a bordo?

Search

Text Color

Text Size

Margin Size

Font Type