7.7: Integrales inadecuadas

Objetivos de aprendizaje

• Evaluar una integral en un intervalo infinito.
• Evaluar una integral en un intervalo cerrado con una discontinuidad infinita dentro del intervalo.
• Utilice el teorema de comparación para determinar si una integral definida es convergente.

¿El área entre la gráfica de$f(x)=\dfrac{1}{x}$ y el$x$ eje sobre el intervalo es$[1,+∞)$ finita o infinita? Si esta misma región gira alrededor del$x$ eje -eje, ¿el volumen es finito o infinito? Sorprendentemente, el área de la región descrita es infinita, pero el volumen del sólido obtenido al girar esta región alrededor del$x$ eje es finito.

En esta sección, definimos integrales a lo largo de un intervalo infinito así como integrales de funciones que contienen una discontinuidad en el intervalo. Las integrales de estos tipos se denominan integrales inpropias. Examinamos varias técnicas para evaluar integrales inadecuadas, todas las cuales implican tomar límites.

Integración a través de un Intervalo Infinito

¿Cómo debemos ir definiendo una integral del tipo$\displaystyle \int ^{+∞}_af(x)\,dx?$ Podemos integrar$\displaystyle \int ^t_af(x)\,dx$ por cualquier valor de$t$, por lo que es razonable mirar el comportamiento de esta integral a medida que sustituimos valores mayores de$t$. La figura$\PageIndex{1}$ muestra que$\displaystyle \int ^t_af(x)\,dx$ puede interpretarse como área para diversos valores de$t$. En otras palabras, podemos definir una integral impropia como un límite, tomado como uno de los límites de integración aumenta o disminuye sin límite.

Figura$\PageIndex{1}$: Para integrar una función a lo largo de un intervalo infinito, consideramos el límite de la integral a medida que el límite superior aumenta sin límite.

Definición: integral impropia

1. Dejar$f(x)$ ser continuo a lo largo de un intervalo de la forma$[a,+∞)$. Entonces $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx, \label{improper1}$$ siempre que exista este límite.
2. Dejar$f(x)$ ser continuo a lo largo de un intervalo de la forma$(−∞,b]$. Entonces $$\int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx, \label{improper2}$$ siempre que exista este límite.

En cada caso, si existe el límite, entonces se dice que la integral impropia converge. Si el límite no existe, entonces se dice que la integral impropia diverge.

3. Dejar$f(x)$ ser continuo sobre$(−∞,+∞)$. Entonces $$\int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx, \label{improper3}$$ siempre que eso$\displaystyle \int ^0_{−∞}f(x)\,dx$ y$\displaystyle \int ^{+∞}_0f(x)\,dx$ ambos converjan. Si alguna de estas dos integrales diverge, entonces$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx$ diverge. (Se puede demostrar que, de hecho,$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^a_{−∞}f(x)\,dx+\int ^{+∞}_af(x)\,dx$ por cualquier valor de a.).

En nuestro primer ejemplo, volvemos a la pregunta que planteamos al inicio de esta sección: ¿El área entre la gráfica de$f(x)=\frac{1}{x}$ y el$x$ eje -sobre el intervalo es$[1,+∞)$ finita o infinita?

Ejemplo$\PageIndex{1}$: Finding an Area

Determinar si el área entre la gráfica de$f(x)=\dfrac{1}{x}$ y el$x$ eje -sobre el intervalo$[1,+∞)$ es finita o infinita.

Solución

Primero hacemos un boceto rápido de la región en cuestión, como se muestra en la Figura$\PageIndex{2}$.

Figura$\PageIndex{2}$: Podemos encontrar el área entre la curva$f(x)=1/x$ y el$x$ eje -en un intervalo infinito.

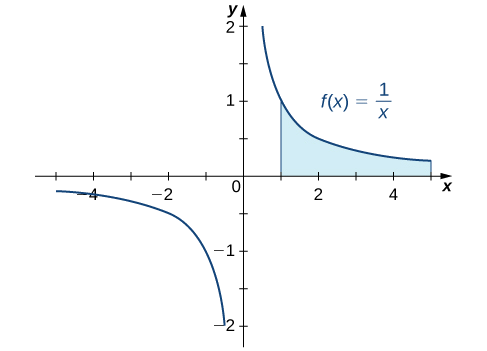
Podemos ver que la zona de esta región viene dada por

$$A=\int ^∞_1\frac{1}{x}\,dx. \nonumber$$

que se puede evaluar usando la ecuación\ ref {improper1}:

$$\begin{align*} A =\int ^∞_1\frac{1}{x}\,dx \nonumber \\[4pt] =\lim_{t→+∞}\int ^t_1\frac{1}{x}\,dx \tag{Rewrite the improper integral as a limit} \\[4pt] =\lim_{t→+∞}\ln |x|∣^t_1 \tag{Find the antiderivative} \\[4pt] =\lim_{t→+∞}(\ln |t|−\ln 1) \tag{Evaluate the antiderivative} \\[4pt] =+∞. \tag{Evaluate the limit.} \end{align*}$$

Dado que la integral impropia diverge a$+∞,$ la zona de la región es infinita.

Ejemplo$\PageIndex{2}$: Finding a Volume

Encuentra el volumen del sólido obtenido al girar la región delimitada por la gráfica de$f(x)=\dfrac{1}{x}$ y el$x$ eje -sobre el intervalo$[1,+∞)$ alrededor del$x$ eje -eje.

Solución

El sólido se muestra en la Figura$\PageIndex{3}$. Usando el método del disco, vemos que el volumen$V$ es

$$V=π\int ^{+∞}_1\frac{1}{x^2}\,dx. \nonumber$$

Figura$\PageIndex{3}$: El sólido de revolución se puede generar rotando un área infinita alrededor del$x$ eje.

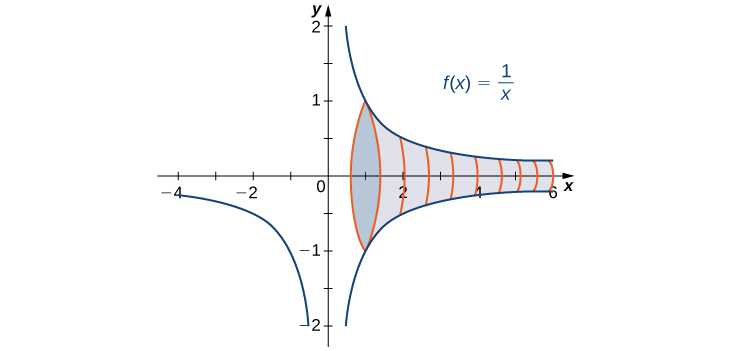
Entonces tenemos

\ [\ displaystyle\ begin {align*} V &=π\ int ^ {+∞} _1\ frac {1} {x^2}\, dx\\ [4pt]
&=π\ lim_ {t→+∞}\ int ^t_1\ frac {1} {x^2}\, dx\ quad\ text {Reescribir como límite.}\\ [4pt]
=π\ lim_ {t→+∞} −\ frac {1} {x} ^t_1\ quad\ text {Encuentra la antiderivada.}\\ [4pt]
&=π\ lim_ {t→+∞}\ left (− \ frac {1} {t} +1\ derecha)\ quad\ text {Evaluar la antiderivada.}\\ [4pt]
&=π\ end {align*}\]

La integral impropia converge a$π$. Por lo tanto, el volumen del sólido de la revolución es$π$.

En conclusión, aunque el área de la región entre el$x$ eje -eje y la gráfica de$f(x)=1/x$ sobre el intervalo$[1,+∞)$ es infinita, el volumen del sólido generado al girar esta región alrededor del$x$ eje es finito. El sólido generado se conoce como Cuerno de Gabriel.

Nota: El cuerno de Gabriel (también llamado trompeta de Torricelli) es una figura geométrica que tiene una superficie infinita, pero un volumen finito. El nombre hace referencia a la tradición identificando al Arcángel Gabriel como el ángel que toca el cuerno para anunciar el Día del Juicio, asociando lo divino, o infinito, con lo finito. Las propiedades de esta figura fueron estudiadas por primera vez por el físico y matemático italiano Evangelista Torricelli en el siglo XVII.

Ejemplo$\PageIndex{3}$: Traffic Accidents in a City

Supongamos que en una intersección transitada, los accidentes de tránsito ocurren a una tasa promedio de uno cada tres meses. Después de que vecinos se quejaron, se realizaron cambios en los semáforos en el cruce. Ya han pasado ocho meses desde que se hicieron los cambios y no ha habido accidentes. ¿Los cambios fueron efectivos o el intervalo de 8 meses sin accidente es resultado de casualidad?

Figura$\PageIndex{4}$: Modificación de obra de David McKelvey, Flickr.

La teoría de la probabilidad nos dice que si el tiempo promedio entre eventos es$k$, la probabilidad de que$X$, el tiempo entre eventos, esté entre$a$ y$b$ viene dada por

$$(P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

donde

$$f(x)=\begin{cases}0, \text{if}\;x<0\\ke^{−kx}, \text{if}\;x≥0\end{cases}. \nonumber$$

Así, si los accidentes ocurren a una tasa de uno cada 3 meses, entonces la probabilidad de que$X$, el tiempo entre accidentes, esté entre$a$ y$b$ viene dada por

$$P(a≤x≤b)=\int ^b_af(x)\,dx \nonumber$$

donde $$f(x)=\begin{cases}0, \text{if}\;x<0\\3e^{−3x}, \text{if}\;x≥0\end{cases}. \nonumber$$

Para responder a la pregunta, debemos calcular$\displaystyle P(X≥8)=\int ^{+∞}_83e^{−3x}\,dx$ y decidir si es probable que hayan pasado 8 meses sin accidente si no hubiera habido mejoría en la situación de tránsito.

Solución

Necesitamos calcular la probabilidad como una integral inadecuada:

\ (\ displaystyle\ begin {alinear*} P (X≥8) =\ int ^ {+∞} _83e^ {−3x}\, dx\\ [4pt]
=\ lim_ {t→+∞}\ int ^t_83e^ {−3x}\, dx\\ [4pt]
=\ lim_ {t→+∞} −e^ {−3x} t_8\\ [4pt]
=\ lim_ {t→+∞} (−e^ {−3t} +e^ {−24})\\ [4pt]
≈3.8×10^ {−11}. \ end {alinear*}\)

El valor$3.8×10^{−11}$ representa la probabilidad de que no haya accidentes en 8 meses bajo las condiciones iniciales. Dado que este valor es muy, muy pequeño, es razonable concluir que los cambios fueron efectivos.

Ejemplo$\PageIndex{4}$: Evaluating an Improper Integral over an Infinite Interval

Evaluar$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx.$ Estado si la integral inadecuada converge o diverge.

Solución

Comience reescribiendo$\displaystyle \int ^0_{−∞}\frac{1}{x^2+4}\,dx$ como límite usando la ecuación\ ref {improper2} de la definición. Por lo tanto,

\ [\ begin {alinear*}\ int ^0_ {−∞}\ frac {1} {x^2+4}\, dx &=\ lim_ {t→−∞}\ int ^0_t\ frac {1} {x^2+4}\, dx\ quad\ text {Reescribe como límite.}\\ [4pt]
&=\ lim_ {t→−∞} frac {1} {2}\ tan^ {−1}\ frac {x} {2} ^0_t\ quad\ text {Encuentra la antiderivada.}\\ [4pt]
&=\ lim_ {t→−∞}\ left (\ frac {1} {2}\ tan^ {−1} 0−\ frac {1} {2}\ tan^ {−1}\ frac {t} {2}\ derecha)\ quad\ text {Evalúa la antiderivada.}\\ [4pt]
&=\ frac {π} {4}. \ quad\ text {Evalúa el límite y simplifica.} \ end {alinear*}\]

La integral impropia converge a$\dfrac{π}{4}.$

Ejemplo$\PageIndex{5}$: Evaluating an Improper Integral on $(−∞,+∞)$

Evaluar$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx.$ Estado si la integral inadecuada converge o diverge.

Solución

Comience dividiendo la integral:

$$\int ^{+∞}_{−∞}xe^x\,dx=\int ^0_{−∞}xe^x\,dx+\int ^{+∞}_0xe^x\,dx. \nonumber$$

Si cualquiera$\displaystyle \int ^0_{−∞}xe^x\,dx$ o$\displaystyle \int ^{+∞}_0xe^x\,dx$ diverge, entonces$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ diverge. Compute cada integral por separado. Para la primera integral,

$\displaystyle \int ^0_{−∞}xe^x\,dx=\lim_{t→−∞}\int ^0_txe^x\,dx$Reescribir como límite.

$=\lim_{t→−∞}(xe^x−e^x)∣^0_t$Utilice la integración por partes para encontrar el antiderivado. (Aquí$u=x$ y$dv=e^x$.)

$=\lim_{t→−∞}(−1−te^t+e^t)$Evaluar el antiderivado.

$=−1.$

Evaluar el límite. Nota:$\displaystyle \lim_{t→−∞}te^t$ es indeterminado de la$0⋅∞$ forma.Así,$\displaystyle \lim_{t→−∞}te^t=\lim_{t→−∞}\frac{t}{e^{−t}}=\lim_{t→−∞}\frac{−1}{e^{−t}}=\lim_{t→−∞}−e^t=0$ por la Regla de L'Hôpital.

La primera integral impropia converge. Para la segunda integral,

$\displaystyle \int ^{+∞}_0xe^x\,dx=\lim_{t→+∞}\int ^t_0xe^x\,dx$Reescribir como límite.

$=\lim_{t→+∞}(xe^x−e^x)∣^t_0$Encuentra el antiderivado.

$=\lim_{t→+∞}(te^t−e^t+1)$Evaluar el antiderivado.

$=\lim_{t→+∞}((t−1)e^t+1)$Reescribir. ($te^t−e^t$es indeterminado.)

$=+∞.$Evaluar el límite.

Así,$\displaystyle \int ^{+∞}_0xe^x\,dx$ diverge. Ya que esta integral diverge,$\displaystyle \int ^{+∞}_{−∞}xe^x\,dx$ diverge también.

Ejercicio$\PageIndex{1}$

Evaluar$\displaystyle \int ^{+∞}_{−3}e^{−x}\,dx.$ Estado si la integral inadecuada converge o diverge.

Pista

$$\int ^{+∞}_{−3}e^{−x}\,dx=\lim_{t→+∞}\int ^t_{−3}e^{−x}\,dx \nonumber$$

Responder

Converge para$e^3.$

Integrando un Integrando Discontinuo

Ahora examinemos integrales de funciones que contienen una discontinuidad infinita en el intervalo sobre el cual se produce la integración. Considerar una integral de la forma$\displaystyle \int ^b_af(x)\,dx,$ donde$f(x)$ es continua sobre$[a,b)$ y discontinua en$b$. Dado que la función$f(x)$ es continua$[a,t]$ para todos los valores de$t$ satisfacción$a \le t<b$, la integral$\displaystyle \int ^t_af(x)\,dx$ se define para todos esos valores de$t$. Por lo tanto, tiene sentido considerar los valores de$\displaystyle \int ^t_af(x)\,dx$ como$t$ enfoques$b$ para$a \le t<b$. Es decir, definimos$\displaystyle \int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx$, siempre que este límite exista. La figura$\PageIndex{5}$ ilustra$\displaystyle \int ^t_af(x)\,dx$ como áreas de regiones para valores de$t$ aproximación$b$.

Figura$\PageIndex{5}$: A medida que t se acerca a b desde la izquierda, el valor del área de a a a t se acerca al área de a a b.

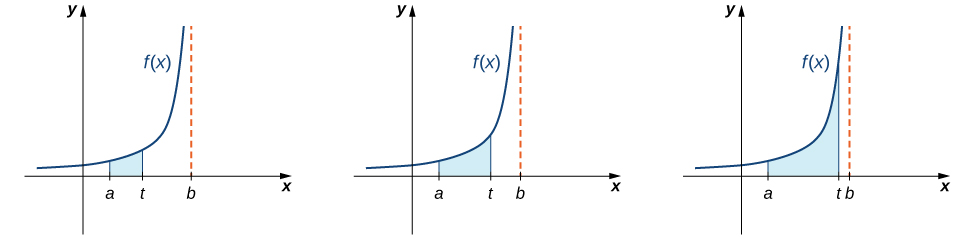
Utilizamos un enfoque similar para definir$\displaystyle \int ^b_af(x)\,dx$, donde$f(x)$ es continuo sobre$(a,b]$ y discontinuo en$a$. Ahora procedemos con una definición formal.

Definición: Integral Inapropiada Convergente y Divergente

1. Dejar$f(x)$ ser continuo sobre$[a,b)$. Entonces, $$\int ^b_af(x)\,dx=\lim_{t→b^−}\int ^t_af(x)\,dx. \label{improperundefb}$$
2. Dejar$f(x)$ ser continuo sobre$(a,b]$. Entonces, $$\int ^b_af(x)\,dx=\lim_{t→a^+}\int ^b_tf(x)\,dx. \label{improperundefa}$$ en cada caso, si existe el límite, entonces se dice que la integral impropia converge. Si el límite no existe, entonces se dice que la integral impropia diverge.
3. Si$f(x)$ es continuo sobre$[a,b]$ excepto en un punto$c$ adentro$(a,b)$, entonces $$\int ^b_af(x)\,dx=\int ^c_af(x)\,dx+\int ^b_cf(x)\,dx,\label{improperundefc}$$ siempre que ambos$\displaystyle \int ^c_af(x)\,dx$ y$\displaystyle \int ^b_cf(x)\,dx$ converjan. Si alguna de estas integrales diverge, entonces$\displaystyle \int ^b_af(x)\,dx$ diverge.

Los siguientes ejemplos demuestran la aplicación de esta definición.

Ejemplo$\PageIndex{6}$: Integrating a Discontinuous Integrand

Evaluar$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx,$ si es posible. Estado si la integral converge o diverge.

Solución

La función$f(x)=\dfrac{1}{\sqrt{4−x}}$ es continua$[0,4)$ y discontinua a 4. Usando la ecuación\ ref {improperundefb} de la definición, reescribe$\displaystyle \int ^4_0\frac{1}{\sqrt{4−x}}\,dx$ como límite:

\ (\ displaystyle\ begin {align*}\ int ^4_0\ frac {1} {\ sqrt {4−x}}\, dx &=\ lim_ {t→4^−}\ int ^t_0\ frac {1} {\ sqrt {4−x}}\, dx\ quad\ text {Reescribir como límite.}\\ [4pt]
&=\ lim_ _ {t→4^−} (−2\ sqrt {4−x}) ^t_0\ quad\ text {Encuentra la antiderivada.}\\ [4pt]
&=\ lim_ {t→4^−} (−2\ sqrt {4−t} +4)\ quad\ text {Evaluar la antiderivada.}\\ [4pt]
&=4. \ quad\ text {Evalúa el límite.} \ end {alinear*}\)

La integral impropia converge.

Ejemplo$\PageIndex{7}$: Integrating a Discontinuous Integrand

Evaluar$\displaystyle \int ^2_0x\ln x\,dx.$ Estado si la integral converge o diverge.

Solución

Dado que$f(x)=x\ln x$ es continuo sobre$(0,2]$ y es discontinuo en cero, podemos reescribir la integral en forma límite usando la ecuación\ ref {improperundefa}:

\ (\ displaystyle\ begin {align*}\ int ^2_0x\ ln x\, dx &=\ lim_ {t→0^+}\ int ^2_tx\ ln x\, dx\ quad\ text {Reescribir como límite.}\\ [4pt]
&=\ lim_ {t→0^+} (\ frac {1} {2} x^2\ ln x−\ frac {1} {4} x^2) ^2_t\ quad\ text {Evaluar}\;\ int x\ ln x\, dx\;\ text {usando integración por partes con}\; u=\ ln x\;\ text {y}\; dv=x. \\ [4pt]
&=\ lim_ {t→0^+} (2\ ln 2−1−\ frac {1} {2} t^2\ ln t+\ frac {1} {4} t^2). \ quad\ text {Evalúa la antiderivada.}\\ [4pt]
&=2\ ln 2−1. \ quad\ text {Evalúa el límite.} \ end {alinear*}\)

Por lo tanto

$\displaystyle \lim_{t→0^+}t^2\ln t\;\text{is indeterminate.}$

Para evaluarlo, reescribir como cociente y aplicar la regla de L'Hôpital.

La integral impropia converge.

Ejemplo$\PageIndex{8}$: Integrating a Discontinuous Integrand

Evaluar$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx.$ Estado si la integral inadecuada converge o diverge.

Solución

Como$f(x)=1/x^3$ es discontinuo a cero, usando la ecuación\ ref {improperundefc}, podemos escribir

$$\int ^1_{−1}\frac{1}{x^3}\,dx=\int ^0_{−1}\frac{1}{x^3}\,dx+\int ^1_0\frac{1}{x^3}\,dx.\nonumber$$

Si alguna de las dos integrales diverge, entonces la integral original diverge. Comience con$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$:

$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx$Reescribir como límite.

$=\lim_{t→0^−}(−\frac{1}{2x^2})∣^t_{−1}$Encuentra el antiderivado.

$=\lim_{t→0^−}(−\frac{1}{2t^2}+\frac{1}{2})$Evaluar el antiderivado.

$=+∞.$Evaluar el límite.

Por lo tanto,$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ diverge. Ya que$\displaystyle \int ^0_{−1}\frac{1}{x^3}\,dx$ diverge,$\displaystyle \int ^1_{−1}\frac{1}{x^3}\,dx$ diverge.

Ejercicio$\PageIndex{2}$

Evaluar$\displaystyle \int ^2_0\frac{1}{x}\,dx.$ Estado si la integral converge o diverge.

Pista

Escribe$\displaystyle \int ^2_0\frac{1}{x}\,dx$ en forma límite usando la ecuación\ ref {improperundefa}.

Responder

$+∞$, diverge.

Un teorema de comparación

No siempre es fácil o incluso posible evaluar directamente una integral impropia; sin embargo, al compararla con otra integral cuidadosamente elegida, puede ser posible determinar su convergencia o divergencia. Para ver esto, considere dos funciones continuas$f(x)$ y$g(x)$ satisfactorias$0≤f(x)≤g(x)$ para$x≥a$ (Figura$\PageIndex{6}$). En este caso, podemos ver las integrales de estas funciones a lo largo de intervalos de la forma$[a,t]$ como áreas, por lo que tenemos la relación

$$0≤\int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx \nonumber$$

para$t≥a$.

Figura$\PageIndex{6}$: Si$0≤f(x)≤g(x)$ para$x≥a$, entonces para$t≥a$,$\displaystyle \int ^t_af(x)\,dx≤\int ^t_ag(x)\,dx.$

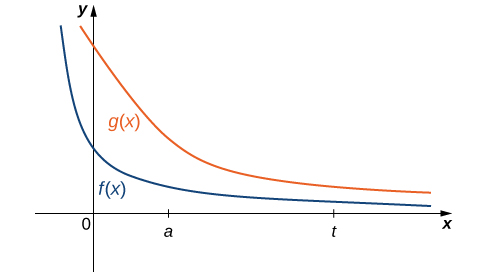
Por lo tanto, si

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$

entonces

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞ \nonumber$$

también. Es decir, si el área de la región entre la gráfica de$f(x)$ y el$x$ eje -sobre$[a,+∞)$ es infinita, entonces el área de la región entre la gráfica de$g(x)$ y el$x$ -eje sobre$[a,+∞)$ es infinita también.

Por otro lado, si

$$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L \nonumber$$

para algún número real$L$, entonces

$$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx \nonumber$$

deben converger a algún valor menor o igual a$L$, ya que$\displaystyle \int ^t_af(x)\,dx$ aumenta como$t$ incrementos y$\displaystyle \int ^t_af(x)\,dx≤L$ para todos$t≥a.$

Si el área de la región entre la gráfica de$g(x)$ y el$x$ eje -sobre$[a,+∞)$ es finita, entonces el área de la región entre la gráfica de$f(x)$ y el$x$ eje -sobre también$[a,+∞)$ es finita.

Estas conclusiones se resumen en el siguiente teorema.

Un teorema de comparación

Dejar$f(x)$ y$g(x)$ ser continuo sobre$[a,+∞).$ Supongamos que$0≤f(x)≤g(x)$ para$x≥a.$

1. Si $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=+∞, \nonumber$$ entonces $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=+∞. \nonumber$$
2. Si $$\int ^{+∞}_ag(x)\,dx=\lim_{t→+∞}\int ^t_ag(x)\,dx=L, \nonumber$$ donde$L$ es un número real, entonces $$\int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx=M \nonumber$$ para algún número real$M≤L.$

Ejemplo$\PageIndex{9}$: Applying the Comparison Theorem

Usa una comparación para mostrar que

$$\int ^{+∞}_1\frac{1}{xe^x}\,dx \nonumber$$

converge.

Solución

Podemos ver que

$$0≤\frac{1}{xe^x}≤\frac{1}{e^x}=e^{−x}, \nonumber$$

así que si$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converge, entonces también lo hace$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx$. Para evaluar$\displaystyle \int ^{+∞}_1e^{−x}\,dx,$ primero reescribirlo como límite:

$\displaystyle \int ^{+∞}_1e^{−x}\,dx=\lim_{t→+∞}\int ^t_1e^{−x}\,dx$

$=\lim_{t→+∞}(−e^{−x})∣^t_1$

$=\lim_{t→+∞}(−e^{−t}+e^{-1})$

$=e^{-1}.$

Ya que$\displaystyle \int ^{+∞}_1e^{−x}\,dx$ converge, también lo hace$\displaystyle \int ^{+∞}_1\frac{1}{xe^x}\,dx.$

Ejemplo$\PageIndex{10}$: Applying the Comparison Theorem

Utilice el teorema de comparación para mostrar que$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ diverge para todos$p<1$.

Solución

Por$p<1, 1/x≤1/(x^p)$ más$[1,+∞).$ En Ejemplo$\PageIndex{1}$, demostramos que$\displaystyle \int ^{+∞}_1\frac{1}{x}\,dx=+∞.$ Por lo tanto,$\displaystyle \int ^{+∞}_1\frac{1}{x^p}\,dx$ diverge para todos$p<1$.

Ejercicio$\PageIndex{3}$

Usa una comparación para mostrar que$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ diverge.

Pista

$\frac{1}{x}≤\frac{\ln x}{x}$en$[e,+∞)$

Responder

Ya que$\displaystyle \int ^{+∞}_e\frac{1}{x}\,dx=+∞,$$\displaystyle \int ^{+∞}_e\frac{\ln x}{x}\,dx$ diverge.

Laplace transforma

En los últimos capítulos, hemos analizado varias formas de utilizar la integración para resolver problemas del mundo real. Para este próximo proyecto, vamos a explorar una aplicación más avanzada de la integración: las transformaciones integrales. Específicamente, describimos la transformación de Laplace y algunas de sus propiedades. La transformación de Laplace se utiliza en ingeniería y física para simplificar los cálculos necesarios para resolver algunos problemas. Toma funciones expresadas en términos de tiempo y las transforma en funciones expresadas en términos de frecuencia. Resulta que, en muchos casos, los cálculos necesarios para resolver problemas en el dominio de la frecuencia son mucho más simples que los requeridos en el dominio del tiempo.

La transformación de Laplace se define en términos de una integral como

$$L{f(t)}=F(s)=\int ^∞_0e^{−st}f(t)dt. \nonumber$$

Tenga en cuenta que la entrada a una transformada de Laplace es una función del tiempo,$f(t),$ y la salida es una función de la frecuencia,$F(s)$. Aunque muchos ejemplos del mundo real requieren el uso de números complejos (involucrando el número imaginario$i=\sqrt{−1}),$ en este proyecto, nos limitamos a funciones de números reales.

Empecemos con un ejemplo sencillo. Aquí calculamos la transformación de Laplace de$f(t)=t$. Tenemos

$$L{t}=\int ^∞_0te^{−st}dt. \nonumber$$

Esta es una integral impropia, por lo que la expresamos en términos de un límite, que da

$$L{t}=\int ^∞_0te^{−st}dt=\lim_{z→∞}\int ^z_0te^{−st}dt. \nonumber$$

Ahora utilizamos la integración por partes para evaluar la integral. Tenga en cuenta que nos estamos integrando con respecto a t, por lo que tratamos la variable s como una constante. Tenemos

$u=t$$du=dt$$dv=e^{−st}dt$$v=−\frac{1}{s}e^{−st}$.

Luego obtenemos

$$\begin{align*} \lim_{z→∞}\int ^z_0te^{−st}dt =\lim_{z→∞}[[−\frac{t}{s}e^{−st}]∣^z_0+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+\frac{0}{s}e^{−0s}]+\frac{1}{s}\int ^z_0e^{−st}dt] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}+0]−\frac{1}{s}[\frac{e^{−st}}{s}]∣^z_0] \\[4pt]\ =\lim_{z→∞}[[−\frac{z}{s}e^{−sz}]−\frac{1}{s^2}[e^{−sz}−1]] \\[4pt]\ =\lim_{z→∞}[−\frac{z}{se^{sz}}]−\lim_{z→∞}[\frac{1}{s^2e^{sz}}]+\lim_{z→∞}\frac{1}{s^2} \\[4pt]\ =0−0+\frac{1}{s^2} \\[4pt]\ =\frac{1}{s^2}. \end{align*}$$

1. Calcular la transformación de Laplace de$f(t)=1.$
2. Calcular la transformación de Laplace de$f(t)=e^{−3t}.$
3. Calcular la transformación de Laplace de$f(t)=t^2$. (Tenga en cuenta que tendrá que integrar por partes dos veces).

Las transformaciones de Laplace se utilizan a menudo para resolver ecuaciones diferenciales. Las ecuaciones diferenciales no se tratan en detalle hasta más adelante en este libro; pero, por ahora, veamos la relación entre la transformada de Laplace de una función y la transformada de Laplace de su derivada.

Empecemos por la definición de la transformación de Laplace. Tenemos

$$L{f(t)}=\int ^∞_0e^{−st}f(t)dt=\lim_{z→∞}\int ^z_0e^{−st}f(t)dt. \nonumber$$

Utilice la integración por partes para evaluar$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}f(t)dt$. (Dejar$u=f(t)$ y$dv=e^{−st}dt$.)

Después de integrar por partes y evaluar el límite, deberías ver que

$$L{f(t)}=\frac{f(0)}{s}+\frac{1}{s}[L{f′(t)}]. \nonumber$$

Entonces,

$$L{f′(t)}=sL{f(t)}−f(0). \nonumber$$

Así, la diferenciación en el dominio del tiempo se simplifica a la multiplicación por s en el dominio de la frecuencia.

Lo último que observamos en este proyecto es cómo se relacionan las transformaciones de Laplace$f(t)$ y sus antiderivadas. Vamos$g(t)=\int ^t_0f(u)du.$ Entonces,

$$L{g(t)}=\int ^∞_0e^{−st}g(t)dt=\lim_{z→∞}\int ^z_0e^{−st}g(t)dt. \nonumber$$

Utilice la integración por partes para evaluar$\displaystyle \lim_{z→∞}\int ^z_0e^{−st}g(t)dt.$ (Let$u=g(t)$ y$dv=e^{−st}dt$. Nota, por la forma en que hemos definido$g(t), du=f(t)dt.$)

Como es de esperar, debería ver que

$$L{g(t)}=\frac{1}{s}⋅L{f(t)}. \nonumber$$

La integración en el dominio del tiempo simplifica la división por$s$ en el dominio de la frecuencia.

Conceptos clave

• Integrales de funciones en intervalos infinitos se definen en términos de límites.
• Integrales de funciones en un intervalo para el cual la función tiene una discontinuidad en un punto final pueden definirse en términos de límites.
• La convergencia o divergencia de una integral impropia puede determinarse comparándola con el valor de una integral impropia por la que se conoce la convergencia o divergencia.

Ecuaciones Clave

• Integrales innecesarias

$\displaystyle \int ^{+∞}_af(x)\,dx=\lim_{t→+∞}\int ^t_af(x)\,dx$

$\displaystyle \int ^b_{−∞}f(x)\,dx=\lim_{t→−∞}\int ^b_tf(x)\,dx$

$\displaystyle \int ^{+∞}_{−∞}f(x)\,dx=\int ^0_{−∞}f(x)\,dx+\int ^{+∞}_0f(x)\,dx$

Glosario

integral inadecuada

una integral sobre un intervalo infinito o una integral de una función que contiene una discontinuidad infinita en el intervalo; una integral inadecuada se define en términos de un límite. La integral inadecuada converge si este límite es un número real finito; de lo contrario, la integral impropia diverge