14.5E: Ejercicios para la Sección 14.5

En los ejercicios 1 - 6, utilice la información proporcionada para resolver el problema.

1) Dejar\( w(x,y,z)=xy\cos z,\) dónde\( x=t,y=t^2,\) y\( z=\arcsin t.\) Encontrar\( \dfrac{dw}{dt}\).

Contestar

\( \dfrac{dw}{dt}=y\cos z+x\cos z(2t)−\dfrac{xy\sin z}{\sqrt{1−t^2}}\)

2) Dejar\( w(t,v)=e^{tv}\) dónde\( t=r+s\) y\( v=rs\). Encontrar\( \dfrac{∂w}{∂r}\) y\( \dfrac{∂w}{∂s}\).

3) Si\( w=5x^2+2y^2, \quad x=−3u+v,\) y\( y=u−4v,\) encontrar\( \dfrac{∂w}{∂u}\) y\( \dfrac{∂w}{∂v}\).

Contestar

\( \dfrac{∂w}{∂u}=−30x+4y \quad\ = \quad -30(-3u + v) + 4(u - 4v) \quad = \quad 90u -30v + 4u - 16v \quad = \quad 94u - 46v\),
\(\dfrac{∂w}{∂v}=10x−16y \quad\ = \quad 10(-3u + v) - 16(u - 4v) \quad = \quad -30u +10v - 16u + 64v \quad = \quad -46u + 74v\)

4) Si\( w=xy^2,x=5\cos(2t),\) y\( y=5\sin(2t)\), encuentra\( \dfrac{∂w}{∂t}\).

5) Si\( f(x,y)=xy,x=r\cos θ,\) y\( y=r\sin θ\), encontrar\(\dfrac{∂f}{∂r}\) y expresar la respuesta en términos de\( r\) y\( θ\).

Contestar

\( \dfrac{∂f}{∂r}=r\sin(2θ)\)

6) Supongamos\( f(x,y)=x+y,u=e^x\sin y,\quad x=t^2\) y\( y=πt\), dónde\( x=r\cos θ\) y\( y=r\sin θ\). Encuentra\( \dfrac{∂f}{∂θ}\).

En los ejercicios 7 - 12, encuentra de dos\( \dfrac{dz}{dt}\) maneras, primero usando la regla de la cadena y luego por sustitución directa.

7)\( z=x^2+y^2, \quad x=t,y=t^2\)

Contestar

\( \dfrac{dz}{dt}=2t+4t^3\)

8)\( z=\sqrt{x^2+y^2},\quad y=t^2,x=t\)

9)\( z=xy,\quad x=1−\sqrt{t},y=1+\sqrt{t}\)

Contestar

\( \dfrac{dz}{dt}=−1\)

10)\( z=\frac{x}{y},\quad x=e^t,y=2e^t\)

11)\( z=\ln(x+y), \quad x=e^t,y=e^t\)

Contestar

\( \dfrac{dz}{dt}=1\)

12)\( z=x^4,\quad x=t,y=t\)

13) Dejar\( w(x,y,z)=x^2+y^2+z^2, \quad x=cost,y=sint,\) y\( z=e^t\). \( w\)Expresar en función de\( t\) y encontrar\( \dfrac{dw}{dt}\) directamente. Luego, encuentra\( \dfrac{dw}{dt}\) usando la regla de la cadena.

Contestar

\( \dfrac{dw}{dt}=2e^{2t}\)en ambos casos

14) Dejar\( z=x^2y,\) dónde\( x=t^2\) y\( y=t^3\). Encuentra\( \dfrac{dz}{dt}\).

15) Dejar\( u=e^x\sin y,\) dónde\( x=-\ln 2t\) y\( y=πt\). Encuentra\( \dfrac{du}{dt}\) cuándo\( x=\ln 2\) y\( y=\frac{π}{4}\).

Contestar

\( \dfrac{du}{dt} = \sqrt{2}\big(\pi - 4\big)\)

En los ejercicios 16 - 33, encuentra\( \dfrac{dy}{dx}\) usando derivadas parciales.

16)\( \sin(6x)+\tan(8y)+5=0\)

17)\( x^3+y^2x−3=0\)

Contestar

\( \dfrac{dy}{dx}=−\dfrac{3x^2+y^2}{2xy}\)

18)\( \sin(x+y)+\cos(x−y)=4\)

19)\( x^2−2xy+y^4=4\)

Contestar

\( \dfrac{dy}{dx}=\dfrac{y−x}{−x+2y^3}\)

20)\( xe^y+ye^x−2x^2y=0\)

21)\( x^{2/3}+y^{2/3}=a^{2/3}\)

Contestar

\( \dfrac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}\)

22)\( x\cos(xy)+y\cos x=2\)

23)\( e^{xy}+ye^y=1\)

Contestar

\( \dfrac{dy}{dx}=−\dfrac{ye^{xy}}{xe^{xy}+e^y(1+y)}\)

24)\( x^2y^3+\cos y=0\)

25) Encontrar\( \dfrac{dz}{dt}\) usando la regla de la cadena donde\( z=3x^2y^3,\,\,x=t^4,\) y\( y=t^2\).

Contestar

\( \dfrac{dz}{dt}=42t^{13}\)

26) Let\( z=3\cos x−\sin(xy),x=\frac{1}{t},\) and\( y=3t.\) Find\( \dfrac{dz}{dt}\).

27) Dejar\( z=e^{1−xy},\,\, x=t^{1/3},\) y\( y=t^3\). Encuentra\( \dfrac{dz}{dt}\).

Contestar

\( \dfrac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}\)

28) Encontrar\( \dfrac{dz}{dt}\) por la regla de la cadena dónde\( z=\cosh^2(xy),\,\,x=\frac{1}{2}t,\) y\( y=e^t\).

29) Let\( z=\dfrac{x}{y},\,\, x=2\cos u,\) y\( y=3\sin v.\) Find\( \dfrac{∂z}{∂u}\) y\( \dfrac{∂z}{∂v}\).

Contestar

\( \dfrac{∂z}{∂u}=\dfrac{−2\sin u}{3\sin v}\)y\( \dfrac{∂z}{∂v}=\dfrac{−2\cos u\cos v}{3\sin^2v}\)

30) Vamos\( z=e^{x^2y}\), dónde\( x=\sqrt{uv}\) y\( y=\frac{1}{v}\). Encontrar\( \dfrac{∂z}{∂u}\) y\( \dfrac{∂z}{∂v}\).

31) Si\( z=xye^{x/y},\,\, x=r\cos θ,\) y\( y=r\sin θ\), encontrar\( \dfrac{∂z}{∂r}\) y\( \dfrac{∂z}{∂θ}\) cuándo\( r=2\) y\( θ=\frac{π}{6}\).

Contestar

\( \dfrac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \dfrac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}\)

32) Encuentra\( \dfrac{∂w}{∂s}\) si\( w=4x+y^2+z^3,\,\,x=e^{rs^2},\,\,y=\ln(\frac{r+s}{t}),\) y\( z=rst^2\).

33) Si\( w=\sin(xyz),\,\,x=1−3t,\,\,y=e^{1−t},\) y\( z=4t\), encuentra\( \dfrac{∂w}{∂t}\).

Contestar

\( \dfrac{∂w}{∂t}=-3yz\cos(xyz)−xze^{1−t}\cos(xyz)+4xy\cos(xyz)\)

En los ejercicios 34 - 36, usa esta información:\( f(x,y)\) Se dice que una función es homogénea de grado\( n\) si\( f(tx,ty)=t^nf(x,y)\). Para todas las funciones homogéneas de grado\( n\), la siguiente ecuación es cierta:\( x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)\). Demostrar que la función dada es homogénea y verificar que\( x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)\).

34)\( f(x,y)=3x^2+y^2\)

35)\( f(x,y)=\sqrt{x^2+y^2}\)

Contestar

\( f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \quad \dfrac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)\)

36)\( f(x,y)=x^2y−2y^3\)

37) El volumen de un cilindro circular derecho viene dado por\( V(x,y)=πx^2y,\) donde\( x\) esta el radio del cilindro y\( y\) es la altura del cilindro. Supongamos\( x\) y\( y\) son funciones de\( t\) dadas por\( x=\frac{1}{2}t\) y\( y=\frac{1}{3}t\) así que\( x\) y ambas\( y\) van aumentando con el tiempo. ¿Qué tan rápido aumenta el volumen cuando\( x=2\) y\( y=5\)? Supongamos que el tiempo se mide en segundos.

Contestar

\( \ddfrac{dV}{dt} = \frac{34π}{3}\,\text{units}^3/\text{s}\)

38) La presión\( P\) de un gas está relacionada con el volumen y la temperatura por la fórmula\( PV=kT\), donde la temperatura se expresa en kelvin. Expresar la presión del gas en función de ambos\( V\) y\( T\). Encuentra\( \dfrac{dP}{dt}\) cuando\( k=1, \dfrac{dV}{dt}=2\) cm ³ /min,\( \dfrac{dT}{dt}=12\) K/min,\( V=20 cm^3\), y\( T=20°F\).

39) El radio de un cono circular derecho aumenta a\( 3\) cm/min mientras que la altura del cono disminuye a\( 2\) cm/min. Encuentra la tasa de cambio del volumen del cono cuando el radio es\( 13\) cm y la altura es\( 18\) cm.

Contestar

\( \dfrac{dV}{dt}=\frac{1066π}{3}\,\text{cm}^3/\text{min}\)

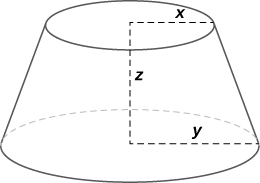
40) El volumen de un cono frustum viene dado por la fórmula\( V=\frac{1}{3}πz(x^2+y^2+xy),\) donde\( x\) está el radio del círculo más pequeño,\( y\) es el radio del círculo más grande, y\( z\) es la altura del cono (ver figura). Encuentra la tasa de cambio del volumen de este tronco cuando\( x=10\) en.,\(y=12\) en., y\( z=18\) en.

41) Una caja cerrada tiene la forma de un sólido rectangular con dimensiones\( x,y,\) y\( z\). (Las dimensiones están en pulgadas.) Supongamos que cada dimensión está cambiando a la velocidad de\( 0.5\) in. /min. Encuentre la tasa de cambio de la superficie total de la caja cuando esté\( x=2\) en.,\(y=3\) in., y\( z=1\) en.

Contestar

\( \dfrac{dA}{dt}=12\, \text{in.}^2/\text{min}\)

42) La resistencia total en un circuito que tiene tres resistencias individuales representadas por\( x,y,\) y\( z\) viene dada por la fórmula\( R(x,y,z)=\dfrac{xyz}{yz+xz+xy}\). Supongamos que en un momento dado la\( x\) resistencia es\( 100\,Ω\), la\( y\) resistencia es\( 200\,Ω,\) y la\( z\) resistencia es\( 300\,Ω.\) También, supongamos que la\( x\) resistencia está cambiando a una velocidad de\( 2\,Ω/\text{min},\) la\( y\) resistencia está cambiando a la velocidad de\( 1\,Ω/\text{min}\), y la \( z\)la resistencia no tiene ningún cambio. Encuentra la tasa de cambio de la resistencia total en este circuito en este momento.

43) La temperatura\( T\) en un punto\( (x,y)\) es\( T(x,y)\) y se mide usando la escala Celsius. Una mosca se arrastra para que su posición después de\( t\) segundos sea dada por\( x=\sqrt{1+t}\) y\( y=2+\frac{1}{3}t\), donde\( x\) y\( y\) se midan en centímetros. La función de temperatura satisface\( T_x(2,3)=4\) y\( T_y(2,3)=3\). ¿Qué tan rápido aumenta la temperatura en el camino de la mosca después de\( 3\) segundos?

Contestar

\( 2\)°C/seg

44) Los\( y\) componentes\( x\) y de un fluido que se mueve en dos dimensiones vienen dados por las siguientes funciones:\( u(x,y)=2y\) y\( v(x,y)=−2x\) con\(x≥0\) y\(y≥0\). La velocidad del fluido en el punto\( (x,y)\) es\( s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}\). Buscar\( \dfrac{∂s}{∂x}\) y\( \dfrac{∂s}{∂y}\) usar la regla de la cadena.

45) Let\( u=u(x,y,z),\) where\( x=x(w,t),\, y=y(w,t),\, z=z(w,t),\, w=w(r,s)\), y\( t=t(r,s).\) Use un diagrama de árbol y la regla de cadena para encontrar una expresión para\( \dfrac{∂u}{∂r}\).

Contestar

\( \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})\)