15.7: Cambio de Variables en Integrales Múltiples
- Page ID
- 116276
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Determinar la imagen de una región bajo una transformación dada de variables.
- Calcular el jacobiano de una transformación dada.
- Evaluar una doble integral usando un cambio de variables.
- Evaluar una triple integral utilizando un cambio de variables.
Recordar de Sustitución Regla el método de integración por sustitución. Al evaluar una integral como
\[\int_2^3 x(x^2 - 4)^5 dx, \nonumber \]
sustituimos\(u = g(x) = x^2 - 4\). Entonces\(du = 2x \, dx\) o\(x \, dx = \frac{1}{2} du\) y los límites cambian a\(u = g(2) = 2^2 - 4 = 0\) y\(u = g(3) = 9 - 4 = 5\). Así la integral se convierte
\[\int_0^5 \frac{1}{2}u^5 du \nonumber \]
y esta integral es mucho más sencilla de evaluar. Es decir, al resolver problemas de integración, hacemos las sustituciones adecuadas para obtener una integral que se vuelve mucho más simple que la integral original.
También usamos esta idea cuando transformamos integrales dobles en coordenadas rectangulares en coordenadas polares y transformamos integrales triples en coordenadas rectangulares en coordenadas cilíndricas o esféricas para hacer los cálculos más simples. De manera más general,
\[\int_a^b f(x) dx = \int_c^d f(g(u))g'(u) du, \nonumber \]
Dónde\(x = g(u), \, dx = g'(u) du\), y\(u = c\) y\(u = d\) satisfacer\(c = g(a)\) y\(d = g(b)\).
Un resultado similar ocurre en dobles integrales cuando sustituimos
- \(x = f (r,\theta) = r \, \cos \, \theta\)
- \( y = g(r, \theta) = r \, \sin \, \theta\), y
- \(dA = dx \, dy = r \, dr \, d\theta\).
Entonces conseguimos
\[\iint_R f(x,y) dA = \iint_S (r \, \cos \, \theta, \, r \, \sin \, \theta)r \, dr \, d\theta \nonumber \]
donde el dominio\(R\) es reemplazado por el dominio\(S\) en coordenadas polares. Generalmente, la función que utilizamos para cambiar las variables para simplificar la integración se denomina transformación o mapeo.
Transformaciones Planares
Una transformación plana\(T\) es una función que transforma una región\(G\) en un plano en una región\(R\) en otro plano mediante un cambio de variables. Ambos\(G\) y\(R\) son subconjuntos de\(R^2\). Por ejemplo, Figura\(\PageIndex{1}\) muestra una región\(G\) en el\(uv\) -plano transformada en una región\(R\) en el\(xy\) -plano por el cambio de variables\(x = g(u,v)\) y\(y = h(u,v)\), o a veces escribimos\(x = x(u,v)\) y\(y = y(u,v)\). Normalmente asumiremos que cada una de estas funciones tiene primeras derivadas parciales continuas, lo que significa\(g_u, \, g_v, \, h_u,\) y\(h_v\) existen y también son continuas. Pronto quedará clara la necesidad de este requisito.
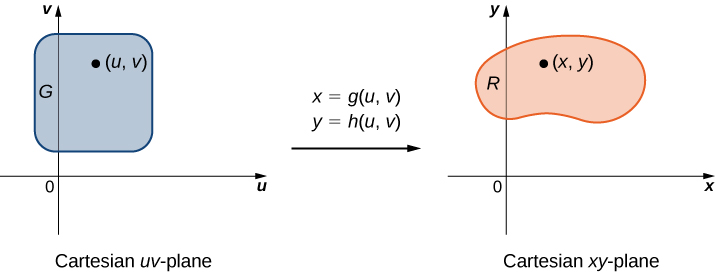
Una transformación\(T: \, G \rightarrow R\), definida como\(T(u,v) = (x,y)\), se dice que es una transformación uno a uno si no hay dos puntos mapeados al mismo punto de imagen.
Para mostrar que\(T\) es una transformación uno a uno, asumimos\(T(u_1,v_1) = T(u_2, v_2)\) y mostramos que como consecuencia obtenemos\((u_1,v_1) = (u_2, v_2)\). Si la transformación\(T\) es uno a uno en el dominio\(G\), entonces la inversa\(T^{-1}\) existe con el dominio\(R\) tal que\(T^{-1} \circ T\) y\(T \circ T^{-1}\) son funciones de identidad.
La figura\(\PageIndex{2}\) muestra el mapeo\(T(u,v) = (x,y)\) donde\(x\) y\(y\) están relacionados con\(u\) y\(v\) por las ecuaciones\(x = g(u,v)\) y\(y = h(u,v)\). La región\(G\) es el dominio de\(T\) y la región\(R\) es el rango de\(T\), también conocida como la imagen de\(G\) bajo la transformación\(T\).
Supongamos que una transformación\(T\) se define como\(T(r,\theta) = (x,y)\) dónde\(x = r \, \cos \, \theta, \, y = r \, \sin \, \theta\). Encuentra la imagen del rectángulo polar\(G = \{(r,\theta) | 0 \leq r \leq 1, \, 0 \leq \theta \leq \pi/2\}\) en el\(r\theta\) plano -a una región\(R\) en el\(xy\) plano. Demostrar que\(T\) es una transformación uno a uno en\(G\) y encontrar\(T^{-1} (x,y)\).
Solución
Ya que\(r\) varía de 0 a 1 en el\(r\theta\) plano -tenemos un disco circular de radio 0 a 1 en el\(xy\) plano -plano. Debido a que\(\theta\) varía de 0 a\(\pi/2\) en el\(r\theta\) plano, terminamos obteniendo un cuarto de círculo de radio\(1\) en el primer cuadrante del\(xy\) plano -plano (Figura\(\PageIndex{2}\)). De ahí\(R\) un cuarto de círculo delimitado por\(x^2 + y^2 = 1\) en el primer cuadrante.
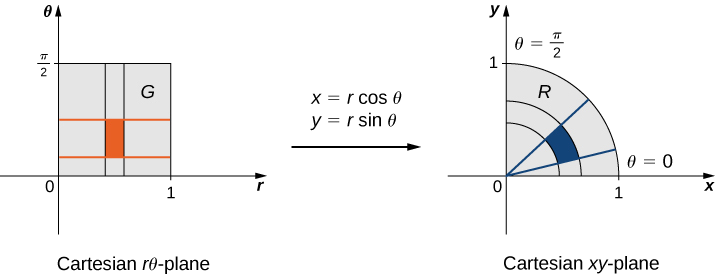
Para mostrar que\(T\) es una transformación uno a uno, asumir\(T(r_1,\theta_1) = T(r_2, \theta_2)\) y mostrar como consecuencia que\((r_1,\theta_1) = (r_2, \theta_2)\). En este caso, tenemos
\[T(r_1,\theta_1) = T(r_2, \theta_2), \nonumber \]
\[(x_1,y_1) = (x_1,y_1), \nonumber \]
\[(r_1 \cos \, \theta_1, r_1 \sin \, \theta_1) = (r_2 \cos \, \theta_2, r_2 \sin \, \theta_2), \nonumber \]
\[r_1 \cos \, \theta_1 = r_2 \cos \, \theta_2, \, r_1 \sin \, \theta_1 = r_2 \sin \, \theta_2. \nonumber \]
Dividiendo, obtenemos
\[\frac{r_1 \cos \, \theta_1}{r_1 \sin \, \theta_1} = \frac{ r_2 \cos \, \theta_2}{ r_2 \sin \, \theta_2} \nonumber \]
\[\frac{\cos \, \theta_1}{\sin \, \theta_1} = \frac{\cos \, \theta_2}{\sin \, \theta_2} \nonumber \]
\[\tan \, \theta_1 = \tan \, \theta_2 \nonumber \]
\[\theta_1 = \theta_2 \nonumber \]
ya que la función tangente es uno-una función en el intervalo\(0 \leq \theta \leq \pi/2\). También, ya que\(0 \leq r \leq 1\), tenemos\(r_1 = r_2, \, \theta_1 = \theta_2\). Por lo tanto,\((r_1,\theta_1) = (r_2, \theta_2)\) y\(T\) es una transformación uno a uno de\(G\) a\(R\).
Para encontrar\(T^{-1}(x,y)\) solución para\(r,\theta\) en términos de\(x,y\). Eso ya lo sabemos\(r^2 = x^2 + y^2\) y\(\tan \, \theta = \frac{y}{x}\). Así\(T^{-1}(x,y) = (r,\theta)\) se define como\(r = \sqrt{x^2 + y^2}\) y\(\tan^{-1} \left(\frac{y}{x}\right)\).
Que la transformación\(T\) se defina por\(T(u,v) = (x,y)\) dónde\(x = u^2 - v^2\) y\(y = uv\). Encuentra la imagen del triángulo en el\(uv\) plano -con vértices\((0,0), \, (0,1)\), y\((1,1)\).
Solución
El triángulo y su imagen se muestran en la Figura\(\PageIndex{3}\). Para entender cómo se transforman los lados del triángulo, llame al lado que une\((0,0)\) y\((0,1)\) lado\(A\), el lado que une\((0,0)\) y\((1,1)\) lado\(B\), y el lado que une\((1,1)\) y\((0,1)\) lado\(C\).
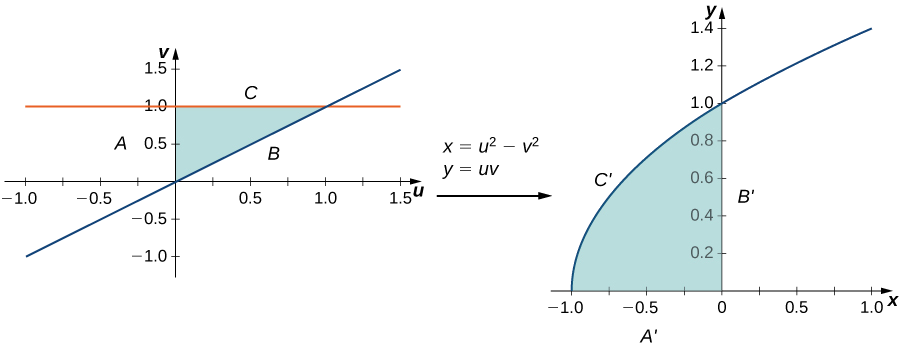
- Para el lado\(A: \, u = 0, \, 0 \leq v \leq 1\) se transforma a\(x = -v^2, \, y = 0\) así que este es el lado\(A'\) que se une\((-1,0)\) y\((0,0)\).
- Para el lado\(B: \, u = v, \, 0 \leq u \leq 1\) se transforma a\(x = 0, \, y = u^2\) así que este es el lado\(B'\) que se une\((0,0)\) y\((0,1)\).
- Para el lado\(C: \, 0 \leq u \leq 1, \, v = 1\) se transforma a\(x = u^2 - 1, \, y = u\) (de ahí\(x = y^2 - 1\) así que este es el lado\(C'\) que hace que la mitad superior del arco parabólico se una\((-1,0)\) y\((0,1)\).
Todos los puntos en toda la región del triángulo en el\(uv\) plano -se mapean dentro de la región parabólica en el\(xy\) plano.
Que una transformación\(T\) se defina como\(T(u,v) = (x,y)\) dónde\(x = u + v, \, y = 3v\). Encuentra la imagen del rectángulo\(G = \{(u,v) : \, 0 \leq u \leq 1, \, 0 \leq v \leq 2\}\) desde el\(uv\) plano -después de la transformación en una región\(R\) en el\(xy\) plano. Demostrar que\(T\) es una transformación uno-a-uno y encontrar\(T^{-1} (x,y)\).
- Pista
-
Sigue los pasos del Ejemplo\(\PageIndex{1B}\).
- Contestar
-
\(T^{-1} (x,y) = (u,v)\)dónde\(u = \frac{3x-y}{3}\) y\(v = \frac{y}{3}\)
Usando la definición, tenemos
\[\Delta A \approx J(u,v) \Delta u \Delta v = \left|\frac{\partial (x,y)}{\partial (u,v)}\right| \Delta u \Delta v. \nonumber \]
Tenga en cuenta que el jacobiano se denota con frecuencia simplemente por
\[J(u,v) = \frac{\partial (x,y)}{\partial (u,v)}. \nonumber \]
Tenga en cuenta también que
\[ \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \nonumber \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} . \nonumber \]
De ahí que la notación\(J(u,v) = \frac{\partial(x,y)}{\partial(u,v)}\) sugiere que podemos escribir el determinante jacobiano con parciales de\(x\) en la primera fila y parciales de\(y\) en la segunda fila.
Encuentra el jacobiano de la transformación dada en Ejemplo\(\PageIndex{1A}\).
Solución
La transformación en el ejemplo es\(T(r,\theta) = ( r \, \cos \, \theta, \, r \, \sin \, \theta)\) dónde\(x = r \, \cos \, \theta\) y\(y = r \, \sin \, \theta\). Así el jacobiano es
\[J(r, \theta) = \frac{\partial(x,y)}{\partial(r,\theta)} = \begin{vmatrix} \dfrac{\partial x}{\partial r} & \dfrac{\partial x}{\partial \theta} \\ \dfrac{\partial y}{\partial r} & \dfrac{\partial y}{\partial \theta} \end{vmatrix} = \begin{vmatrix} \cos \theta & -r\sin \theta \\ \sin \theta & r\cos\theta \end{vmatrix} = r \, \cos^2\theta + r \, \sin^2\theta = r ( \cos^2\theta + \sin^2\theta) = r. \nonumber \]
Encuentra el jacobiano de la transformación dada en Ejemplo\(\PageIndex{1B}\).
Solución
La transformación en el ejemplo es\(T(u,v) = (u^2 - v^2, uv)\) dónde\(x = u^2 - v^2\) y\(y = uv\). Así el jacobiano es
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 2u & -2v \\ v & u \end{vmatrix} = 2u^2 + 2v^2. \nonumber \]
Encuentra el jacobiano de la transformación dada en el punto de control anterior:\(T(u,v) = (u + v, 2v)\).
- Pista
-
Sigue los pasos de los dos ejemplos anteriores.
- Contestar
-
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \nonumber \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1 & 1 \nonumber \\ 0 & 2 \end{vmatrix} = 2 \nonumber \]
Cambio de Variables para Integrales Dobles
Ya hemos visto que, bajo el cambio de variables\(T(u,v) = (x,y)\) donde\(x = g(u,v)\) y\(y = h(u,v)\), una pequeña región\(\Delta A\) en el\(xy\) plano se relaciona con el área formada por el producto\(\Delta u \Delta v\) en el\(uv\) plano por la aproximación
\[\Delta A \approx J(u,v) \Delta u, \, \Delta v. \nonumber \]
Ahora volvamos a la definición de doble integral por un minuto:
\[\iint_R f(x,y)fA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A. \nonumber \]
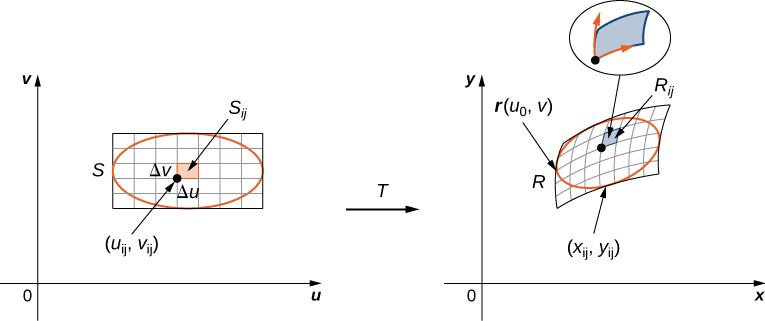
Refiriéndonos a la Figura\(\PageIndex{5}\), observamos que dividimos la región\(S\) en el\(uv\) plano -en pequeños subrectángulos\(S_{ij}\) y dejamos que los subrectángulos\(R_{ij}\) en el\(xy\) plano sean las imágenes de\(S_{ij}\) debajo de la transformación\(T(u,v) = (x,y)\).
Entonces la doble integral se convierte
\[\iint_R = f(x,y)dA = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(x_{ij}, y_{ij}) \Delta A = \lim_{m,n \rightarrow \infty} \sum_{i=1}^m \sum_{j=1}^n f(g(u_{ij}, v_{ij}), \, h(u_{ij}, v_{ij})) | J(u_{ij}, v_{ij})| \Delta u \Delta v. \nonumber \]
Observe que esta es exactamente la suma doble de Riemann para la integral
\[\iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber \]
Deje\(T(u,v) = (x,y)\) dónde\(x = g(u,v)\) y\(y = h(u,v)\) sea una\(C^1\) transformación uno a uno, con un jacobiano distinto de cero en el interior de la región\(S\) en el\(uv\) plano -plano se mapea\(S\) en la región\(R\) en el\(xy\) plano. Si\(f\) es continuo encendido\(R\), entonces
\[\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial (x,y)}{\partial(u,v)}\right| du \, dv. \nonumber \]
Con este teorema para dobles integrales, podemos cambiar las variables de\((x,y)\) a\((u,v)\) en una doble integral simplemente reemplazando
\[dA = dx \, dy = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| du \, dv \nonumber \]
cuando usamos las sustituciones\(x = g(u,v)\)\(y = h(u,v)\) y luego cambiamos los límites de integración en consecuencia. Este cambio de variables a menudo hace que cualquier cálculo sea mucho más simple.
Considerar la integral
\[\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx. \nonumber \]
Utilizar el cambio de variables\(x = r \, \cos \, \theta\) y\(y = r \, \sin \, \theta\), y encontrar la integral resultante.
Solución
Primero necesitamos encontrar la región de integración. Esta región está delimitada por debajo\(y = 0\) y arriba por\(y = \sqrt{2x - x^2}\) (Figura\(\PageIndex{6}\)).
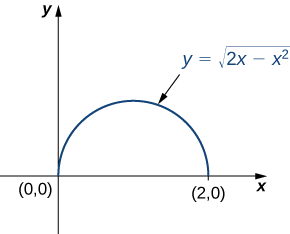
Al cuadrar y recolectar términos, encontramos que la región es la mitad superior del círculo\(x^2 + y^2 - 2x = 0\), es decir\(y^2 + ( x - 1)^2 = 1\). En coordenadas polares, el círculo es\(r = 2 \, cos \, \theta\) así que la región de integración en coordenadas polares está delimitada por\(0 \leq r \leq \cos \, \theta\) y\(0 \leq \theta \leq \frac{\pi}{2}\).
El jacobiano es\(J(r, \theta) = r\), como se muestra en Ejemplo\(\PageIndex{2A}\). Ya que\(r \geq 0\), tenemos\(|J(r,\theta)| = r\).
El integrando\(\sqrt{x^2 + y^2}\) cambia a\(r\) coordenadas polares, por lo que la integral iterada doble es
\[\int_0^2 \int_0^{\sqrt{2x-x^2}} \sqrt{x^2 + y^2} dy \, dx = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r | j(r, \theta)|dr \, d\theta = \int_0^{\pi/2} \int_0^{2 \, cos \, \theta} r^2 dr \, d\theta. \nonumber \]
Considerando el\(\int_0^1 \int_0^{\sqrt{1-x^2}} (x^2 + y^2) dy \, dx,\) uso integral el cambio de variables\(x = r \, cos \, \theta\) y\(y = r \, sin \, \theta\) y encontrar la integral resultante.
- Pista
-
Sigue los pasos del ejemplo anterior.
- Contestar
-
\[\int_0^{\pi/2} \int_0^1 r^3 dr \, d\theta \nonumber \]
Observe en el siguiente ejemplo que la región sobre la que vamos a integrarnos puede sugerir una transformación adecuada para la integración. Esta es una situación común e importante.
Considere la integral\[\iint_R (x - y) dy \, dx, \nonumber \] donde\(R\) está el paralelogramo que une los puntos\((1,2), \, (3,4), \, (4,3)\), y\((6,5)\) (Figura\(\PageIndex{7}\)). Hacer los cambios apropiados de las variables, y escribir la integral resultante.
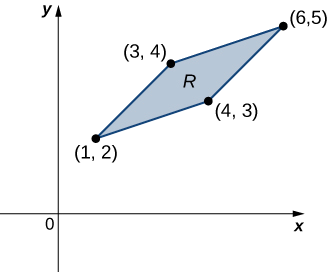
Solución
Primero, tenemos que entender la región sobre la que vamos a integrarnos. Los lados del paralelogramo son\(x - y + 1, \, x - y - 1 = 0, \, x - 3y + 5 = 0\) y\(x - 3y + 9 = 0\) (Figura\(\PageIndex{8}\)). Otra forma de mirarlos es\(x - y = -1, \, x - y = 1, \, x - 3y = -5\), y\(x - 3y = 9\).
Claramente el paralelogramo está delimitado por las líneas\(y = x + 1, \, y = x - 1, \, y = \frac{1}{3}(x + 5)\), y\(y = \frac{1}{3}(x + 9)\).
Observe que si tuviéramos que hacer\(u = x - y\) y\(v = x - 3y\), entonces los límites a la integral serían\(-1 \leq u \leq 1\) y\(-9 \leq v \leq -5\).
Para resolver por\(x\) y\(y\), multiplicamos la primera ecuación por\(3\) y restamos la segunda ecuación,\(3u - v = (3x - 3y) - (x - 3y) = 2x\). Entonces tenemos\(x = \frac{3u-v}{2}\). Además, si simplemente restamos la segunda ecuación de la primera, obtenemos\(u - v = (x - y) - (x - 3y) = 2y\) y\(y = \frac{u-v}{2}\).
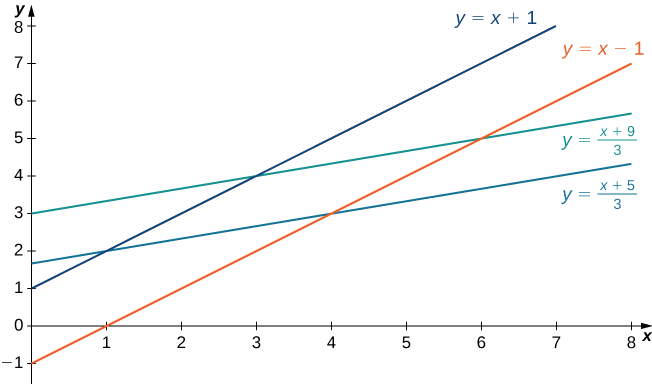
Así, podemos elegir la transformación
\[T(u,v) = \left( \frac{3u - v}{2}, \, \frac{u - v}{2} \right) \nonumber \]y computar el jacobiano\(J(u,v)\). Tenemos
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 3/2 & -1/2 \nonumber \\ 1/2 & -1/2 \end{vmatrix} = -\frac{3}{4} + \frac{1}{4} = - \frac{1}{2} \nonumber \]
Por lo tanto,\(|J(u,v)| = \frac{1}{2}\). Además, el integrand original se convierte en
\[x - y = \frac{1}{2} [3u - v - u + v] = \frac{1}{2} [3u - u] = \frac{1}{2}[2u] = u. \nonumber \]
Por lo tanto, por el uso de la transformación\(T\), la integral cambia a
\[\iint_R (x - y) dy \, dx = \int_{-9}^{-5} \int_{-1}^1 J (u,v) u \, du \, dv = \int_{-9}^{-5} \int_{-1}^1\left(\frac{1}{2}\right) u \, du \, dv, \nonumber \]que es mucho más sencillo de calcular.
Hacer los cambios apropiados de las variables en la integral\[\iint_R \frac{4}{(x - y)^2} dy \, dx, \nonumber \] donde\(R\) está el trapecio delimitado por las líneas\(x - y = 2, \, x - y = 4, \, x = 0\), y\(y = 0\). Escribe la integral resultante.
- Pista
-
Sigue los pasos del ejemplo anterior.
- Contestar
-
\(x = \frac{1}{2}(v + u)\)y\(y = \frac{1}{2} (v - u)\)
y
\[\int_{2}^4 \int_{-u}^u \left(\frac{1}{2}\right)\cdot\frac{4}{u^2} \,dv \, du. \nonumber \]
Estamos listos para dar una estrategia de resolución de problemas para el cambio de variables.
- Esboza la región dada por el problema en el\(xy\) plano -y luego escribe las ecuaciones de las curvas que forman el límite.
- Dependiendo de la región o del integrando, elija las transformaciones\(x = g(u,v)\) y\(y = h(u,v)\).
- Determinar los nuevos límites de integración en el\(uv\) plano.
- Encuentra al jacobiano\(J (u,v)\).
- En el integrando, sustituir las variables para obtener el nuevo integrando.
- Reemplazar\(dy \, dx\) o\(dx \, dy\), lo que ocurra, por\(J(u,v) du \, dv\).
En el siguiente ejemplo, encontramos una sustitución que hace que el integrando sea mucho más sencillo de calcular.
Utilizando el cambio de variables\(u = x - y\) y\(v = x + y\), evaluar la integral\[\iint_R (x - y)e^{x^2-y^2} dA, \nonumber \] donde\(R\) está la región delimitada por las líneas\(x + y = 1\) y\(x + y = 3\) y las curvas\(x^2 - y^2 = -1\) y\(x^2 - y^2 = 1\) (ver la primera región en la Figura\(\PageIndex{9}\)).
Solución
Como antes, primero encuentra la región\(R\) e imagina la transformación para que sea más fácil obtener los límites de integración después de que se realicen las transformaciones (Figura\(\PageIndex{9}\)).
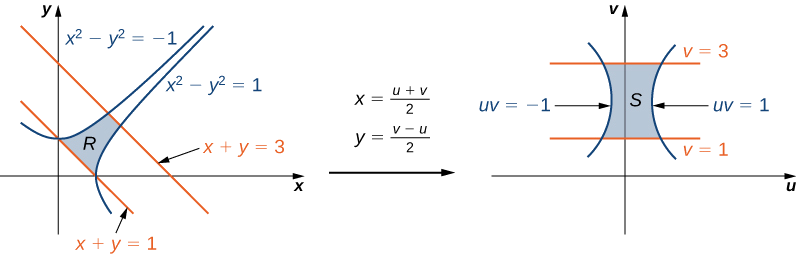
Dado\(u = x - y\) y\(v = x + y\), tenemos\(x = \frac{u+v}{2}\) y\(y = \frac{v-u}{2}\) y de ahí la transformación a usar es\(T(u,v) = \left(\frac{u+v}{2}, \, \frac{v-u}{2}\right)\). Las líneas\(x + y = 1\) y\(x + y = 3\) se convierten\(v = 1\) y\(v = 3\), respectivamente. Las curvas\(x^2 - y^2 = 1\) y\(x^2 - y^2 = -1\) se convierten\(uv = 1\) y\(uv = -1\), respectivamente.
Así podemos describir la región\(S\) (ver la segunda región Figura\(\PageIndex{9}\)) como
\[S = \left\{ (u,v) | 1 \leq v \leq 3, \, \frac{-1}{v} \leq u \leq \frac{1}{v}\right\}. \nonumber \]
El jacobiano para esta transformación es
\[J(u,v) = \frac{\partial(x,y)}{\partial(u,v)} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \begin{vmatrix} 1/2 & 1/2 \\ -1/2 & 1/2 \end{vmatrix} = \frac{1}{2}. \nonumber \]
Por lo tanto, al utilizar la transformación\(T\), la integral cambia a
\[\iint_R (x - y)e^{x^2-y^2} dA = \frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv. \nonumber \]
Haciendo la evaluación, tenemos
\[\frac{1}{2} \int_1^3 \int_{-1/v}^{1/v} ue^{uv} du \, dv = \frac{2}{3e} \approx 0.245. \nonumber \]
Utilizando las sustituciones\(x = v\) y\(y = \sqrt{u + v}\), evaluar la integral\(\displaystyle\iint_R y \, \sin (y^2 - x) \,dA,\) donde\(R\) está la región delimitada por las líneas\(y = \sqrt{x}, \, x = 2\) y\(y = 0\).
- Pista
-
Esboza una imagen y encuentra los límites de la integración.
- Contestar
-
\(\frac{1}{2} (\sin 2 - 2)\)
Cambio de Variables para Integrales Triples
Cambiar variables en triples integrales funciona exactamente de la misma manera. Las sustituciones de coordenadas cilíndricas y esféricas son casos especiales de este método, que aquí demostramos.
Supongamos que\(G\) es una región en\(uvw\) -espacio y se mapea\(D\) en\(xyz\) -espacio (Figura\(\PageIndex{10}\)) por una\(C^1\) transformación uno a uno\(T(u,v,w) = (x,y,z)\) donde\(x = g(u,v,w), \, y = h(u,v,w)\), y\(z = k(u,v,w)\).
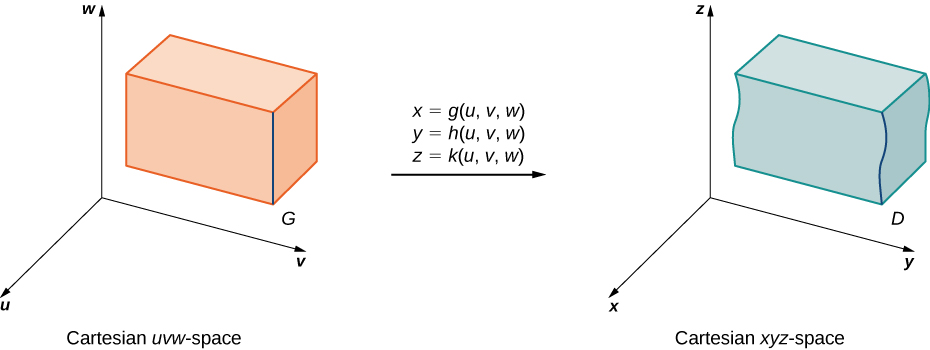
Entonces, cualquier función\(F(x,y,z)\) definida en\(D\) puede considerarse como otra función\(H(u,v,w)\) que se define en\(G\):
\[F(x,y,z) = F(g(u,v,w), \, h(u,v,w), \, k(u,v,w)) = H (u,v,w). \nonumber \]
Ahora necesitamos definir el jacobiano para tres variables.
El determinante jacobiano\(J(u,v,w)\) en tres variables se define de la siguiente manera:
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} & \dfrac{\partial z}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} & \dfrac{\partial z}{\partial v} \\ \dfrac{\partial x}{\partial w} & \dfrac{\partial y}{\partial w} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber \]
Esto también es lo mismo que
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix}. \nonumber \]
El jacobiano también se puede denotar simplemente como\(\frac{\partial(x,y,z)}{\partial (u,v,w)}\).
Con las transformaciones y la jacobiana para tres variables, estamos listos para establecer el teorema que describe el cambio de variables para triples integrales.
Que\(T(u,v,w) = (x,y,z)\) donde\(x = g(u,v,w), \, y = h(u,v,w)\), y\(z = k(u,v,w)\), ser una\(C^1\) transformación uno a uno, con un jacobiano distinto de cero, que mapea la región\(G\) en el\(uvw\) espacio en la región\(D\) en el\(xyz\) -espacio. Como en el caso bidimensional, si\(F\) es continuo encendido\(D\), entonces
\[\begin{align} \iiint_D F(x,y,z) dV = \iiint_G f(g(u,v,w) \, h(u,v,w), \, k(u,v,w)) \left|\frac{\partial (x,y,z)}{\partial (u,v,w)}\right| du \, dv \, dw \\ = \iiint_G H(u,v,w) | J (u,v,w) | du \, dv \, dw. \end{align} \nonumber \]
Veamos ahora cómo los cambios en las integrales triples para coordenadas cilíndricas y esféricas se ven afectados por este teorema. Esperamos obtener las mismas fórmulas que en Integrales triples en Coordenadas Cilíndricas y Esféricas.
Derivar la fórmula en integrales triples para
- cilíndrico y
- coordenadas esféricas.
Solución
A.
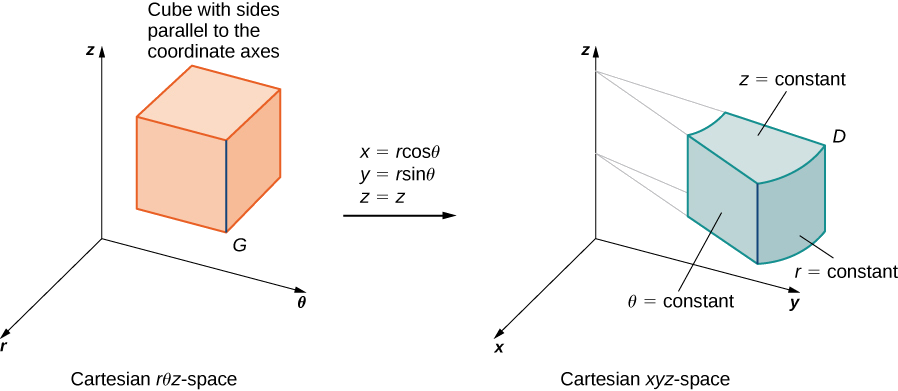
Para las coordenadas cilíndricas, la transformación es\(T (r, \theta, z) = (x,y,z)\) del espacio cartesiano al\(r\theta z\) espacio cartesiano\(xyz\) (Figura\(\PageIndex{11}\)). Aquí\(x = r \, \cos \, \theta, \, y = r \, \sin \theta\) y\(z = z\). El jacobiano para la transformación es
\[J(r,\theta,z) = \frac{\partial (x,y,z)}{\partial (r,\theta,z)} = \begin{vmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial z} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial z} \\ \frac{\partial z}{\partial r} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial z} \end{vmatrix} \nonumber \]
\[ \begin{vmatrix} \cos \theta & -r\sin \theta & 0 \\ \sin \theta & r \cos \theta & 0 \\ 0 & 0 & 1 \end{vmatrix} = r \, \cos^2 \theta + r \, \sin^2 \theta = r. \nonumber \]
Eso lo sabemos\(r \geq 0\), entonces\(|J(r,\theta,z)| = r\). Entonces la triple integral es\[\iiint_D f(x,y,z)dV = \iiint_G f(r \, \cos \theta, \, r \, \sin \theta, \, z) r \, dr \, d\theta \, dz. \nonumber \]
B.
Para las coordenadas esféricas, la transformación es\(T(\rho,\theta,\varphi)\) del\(\rho\theta\varphi\) espacio cartesiano al espacio cartesiano\(xyz\) (Figura\(\PageIndex{12}\)). Aquí\(x = \rho \, \sin \varphi \, \cos \theta, \, y = \rho \, \sin \varphi \, \sin \theta\), y\(z = \rho \, \cos \varphi\). El jacobiano para la transformación es
\[J(\rho,\theta,\varphi) = \frac{\partial (x,y,z)}{\partial (\rho,\theta,\varphi)} = \begin{vmatrix} \frac{\partial x}{\partial \rho} & \frac{\partial x}{\partial \theta} & \frac{\partial x}{\partial \varphi} \\ \frac{\partial y}{\partial \rho} & \frac{\partial y}{\partial \theta} & \frac{\partial y}{\partial \varphi} \\ \frac{\partial z}{\partial \rho} & \frac{\partial z}{\partial \theta} & \frac{\partial z}{\partial \varphi} \end{vmatrix} = \begin{vmatrix} \sin \varphi \cos \theta & -\rho \sin \varphi \sin \theta & \rho \cos \varphi \cos \theta \\ \sin \varphi \sin \theta & \rho \sin \varphi \cos \theta & \rho \cos \varphi \sin \theta \\ \cos \varphi & 0 & -\rho \sin \varphi \end{vmatrix}. \nonumber \]
Ampliando el determinante respecto a la tercera fila:
\ [\ begin {align*} &=\ cos\ varphi\ begin {vmatrix} -\ rho\ sin\ varphi\ sin\ theta &\ rho\ cos\ varphi\ cos\ varphi\ cos\ theta\\ rho\ sin\ varphi\ cos\ theta &\ rho\ cos\ varphi\ sin\ theta\ end {vmatrix} -\ rho\ sin\ varphi\ comenzar {vmatrix}\ sin\ varphi\ cos\ theta & -\ rho\ sin\ varphi\ sin\ theta\\\ sin\ varphi\ sin\ theta &\ rho\ sin\ varphi\ cos\ theta\ end {vmatrix}\\ [4pt]
&=\ cos\ varphi (-\ rho^2\ sin\ varphi\,\ cos\ varphi\,\ sin^2\ theta -\ rho^2\,\ sin\ varphi\,\ cos\ varphi\,\ cos^2 theta\ eta)\\ &\ quad -\ rho\ sin\ varphi (\ rho\ sin^2\ varphi\ cos^2\ theta +\ rho\ sin^2\ varphi\ sin^2\ theta)\\ [4pt]
&=-\ rho^2\ sin\ varphi\ cos^2\ varphi (\ sin^2\ theta +\ cos^2\ theta) -\ rho^2\ sin\ varphi\ sin^2\ varphi (\ sin^2\ theta +\ cos^2\ theta)\\ [4pt]
&= -\ ^2\ sin\ varphi\ cos^2\ varphi -\ rho^2\ sin\ varphi\ sin^2\ varphi\\ [4pt]
&= -\ rho \ sin\ varphi (\ cos^2\ varphi +\ sin^2\ varphi) = -\ rho^2\ sin\ varphi. \ end {alinear*}\]
Ya que\(0 \leq \varphi \leq \pi\), debemos tener\(\sin \varphi \geq 0\). Así\(|J(\rho,\theta, \varphi)| = |-\rho^2 \sin \varphi| = \rho^2 \sin \varphi.\)
.png)
Entonces la triple integral se convierte
\[\iiint_D f(x,y,z) dV = \iiint_G f(\rho \, \sin \varphi \, \cos \theta, \, \rho \, \sin \varphi \, \sin \theta, \rho \, \cos \varphi) \rho^2 \sin \varphi \, d\rho \, d\varphi \, d\theta. \nonumber \]
Probemos otro ejemplo con una sustitución diferente.
Evaluar la triple integral
\[\int_0^3 \int_0^4 \int_{y/2}^{(y/2)+1} \left(x + \frac{z}{3}\right) dx \, dy \, dz \nonumber \]
En el\(xyz\) espacio mediante el uso de la transformación
\(u = (2x - y) /2, \, v = y/2\), y\(w = z/3\).
Luego integrar sobre una región apropiada en\(uvw\) -espacio.
Solución
Como antes, algún tipo de boceto de la región\(G\) en el\(xyz\) espacio sobre el que tenemos que realizar la integración puede ayudar a identificar la región\(D\) en el\(uvw\) espacio (Figura\(\PageIndex{13}\)). Claramente\(G\) en\(xyz\) -espacio está delimitado por los planos\(x = y/2, \, x = (y/2) + 1, \, y = 0, \, y = 4, \, z = 0\), y\(z = 4\). También sabemos que tenemos que usar\(u = (2x - y) /2, \, v = y/2\), y\(w = z/3\) para las transformaciones. Tenemos que resolver para\(x,y\) y\(z\). Aquí nos encontramos con eso\(x = u + v, \, y = 2v\), y\(z = 3w\).
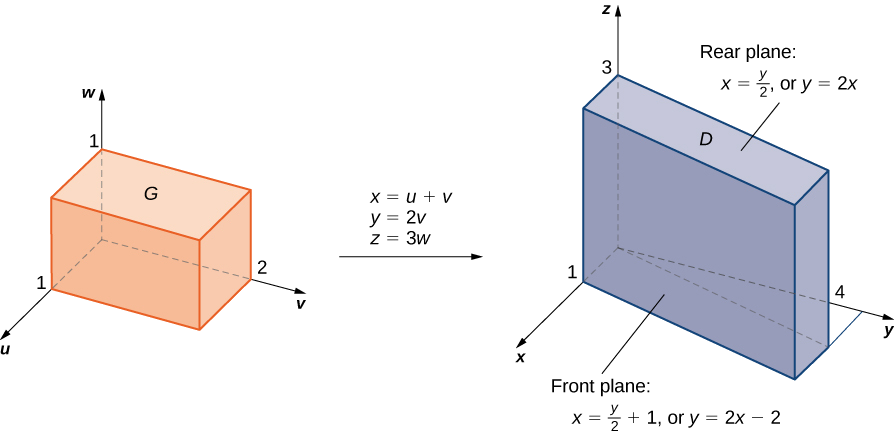
Utilizando álgebra elemental, podemos encontrar las superficies correspondientes para la región\(G\) y los límites de integración en\(uvw\) -espacio. Es conveniente enumerar estas ecuaciones en una tabla.
| Ecuaciones\(xyz\) para la región\(D\) | Ecuaciones correspondientes\(uvw\) para la región\(G\) | Límites para la integración en\(uvw\) |
|---|---|---|
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(x = y/2\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(u + v = 2v/2 = v\) | \ (uvw\)” style="vertical-align:middle; ">\(u = 0\) |
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(x = y/2\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(u + v = (2v/2) + 1 = v + 1\) | \ (uvw\)” style="vertical-align:middle; ">\(u = 1\) |
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(y = 0\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(2v = 0\) | \ (uvw\)” style="vertical-align:middle; ">\(v = 0\) |
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(y = 4\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(2v = 4\) | \ (uvw\)” style="vertical-align:middle; ">\(v = 2\) |
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(z = 0\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(3w = 0\) | \ (uvw\)” style="vertical-align:middle; ">\(w = 0\) |
| \ (xyz\) para la región\(D\) "style="vertical-align:middle;" >\(z = 3\) | \ (uvw\) para la región\(G\) "style="vertical-align:middle;" >\(3w = 3\) | \ (uvw\)” style="vertical-align:middle; ">\(w = 1\) |
Ahora podemos calcular el jacobiano para la transformación:
\[J(u,v,w) = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial x}{\partial v} & \dfrac{\partial x}{\partial w} \\ \dfrac{\partial y}{\partial u} & \dfrac{\partial y}{\partial v} & \dfrac{\partial y}{\partial w} \\ \dfrac{\partial z}{\partial u} & \dfrac{\partial z}{\partial v} & \dfrac{\partial z}{\partial w} \end{vmatrix} = \begin{vmatrix} 1 & 1 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{vmatrix} = 6. \nonumber \]
La función a integrar se convierte en
\[f(x,y,z) = x + \frac{z}{3} = u + v + \frac{3w}{3} = u + v + w. \nonumber \]
Ya estamos listos para armar todo y completar el problema.
\ [\ begin {align*}\ int_0^3\ int_0^4\ int_ {y/2} ^ {(y/2) +1}\ izquierda (x +\ frac {z} {3}\ derecha) dx\, dy\, dz &=\ int_0^1\ int_0^2\ int_0^1 (u + v + w) |J (u, v, w) |du\, dv\, dw\\ [4pt]
&=\ int_0^1\ int_0^2\ int_0^1 (u + v + w) |6|du\, dv\, dw\\ [4pt]
&= 6\ int_0^1\ int_0^2\ int_ 0^1 (u + v + w)\, du\, dv\, dw\\ [4pt]
&= 6\ int_0^1\ int_0^2\ left [\ frac {u^2} {2} + vu + wu\ derecha] _0^1\, dv\, dw\ [4pt]
&= 6\ int_0^1\ int_0^2\ izquierda (\ frac {1} {2} + v + u\ derecha) dv\, dw\\ [4pt]
&= 6\ int_0^1\ left [\ frac {1} {2} v +\ frac {v^2} {2} + wv\ derecha] _0^2 dw\\ [4pt]
&= 6\ int_0^1 (3 + 2w)\, dw = 6\ Grande [3w + w^2\ Grande] _0^1 = 24. \ end {alinear*}\]
Dejar\(D\) ser la región en\(xyz\) -espacio definida por\(1 \leq x \leq 2, \, 0 \leq xy \leq 2\), y\(0 \leq z \leq 1\).
Evaluar\(\iiint_D (x^2 y + 3xyz) \, dx \, dy \, dz\) mediante el uso de la transformación\(u = x, \, v = xy\), y\(w = 3z\).
- Pista
-
Hacer una tabla para cada superficie de las regiones y decidir los límites, como se muestra en el ejemplo.
- Contestar
-
\[\int_0^3 \int_0^2 \int_1^2 \left(\frac{v}{3} + \frac{vw}{3u}\right) du \, dv \, dw = 2 + \ln 8 \nonumber \]
Conceptos clave
- Una transformación\(T\) es una función que transforma una región\(G\) en un plano (espacio) en una región\(R\). en otro plano (espacio) por un cambio de variables.
- Una transformación\(T: G \rightarrow R\) definida como\(T(u,v) = (x,y)\) (o\(T(u,v,w) = (x,y,z))\) se dice que es una transformación uno a uno si no hay dos puntos mapeados al mismo punto de imagen.
- Si\(f\) es continuo encendido\(R\), entonces\[\iint_R f(x,y) dA = \iint_S f(g(u,v), \, h(u,v)) \left|\frac{\partial(x,y)}{\partial (u,v)}\right| du \, dv. \nonumber \]
- Si\(F\) es continuo encendido\(R\), entonces\[\begin{align*}\iiint_R F(x,y,z) \, dV &= \iiint_G F(g(u,v,w), \, h(u,v,w), \, k(u,v,w) \left|\frac{\partial(x,y,z)}{\partial (u,v,w)}\right| \,du \, dv \, dw \\[4pt] &= \iiint_G H(u,v,w) |J(u,v,w)| \, du \, dv \, dw. \end{align*}\]
[T] Los óvalos de Lamé (o superelipses) son curvas planas de ecuaciones\(\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1\), donde a, b y n son números reales positivos.
a. Utilice un CAS para graficar las regiones\(R\) delimitadas por óvalos de Lamé para\(a = 1, \, b = 2, \, n = 4\) y\(n = 6\) respectivamente.
b. Encuentra las transformaciones que mapean la región\(R\) delimitada por el óvalo de Lamé\(x^4 + y^4 = 1\) también llamado ardilla y graficada en la siguiente figura, en el disco unitario.
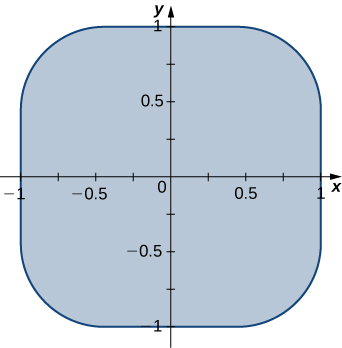
c. Usar un CAS para encontrar una aproximación del área\(A (R)\) of the region \(R\) bounded by \(x^4 + y^4 = 1\). Round your answer to two decimal places.
[T] Lamé ovals have been consistently used by designers and architects. For instance, Gerald Robinson, a Canadian architect, has designed a parking garage in a shopping center in Peterborough, Ontario, in the shape of a superellipse of the equation \(\left(\frac{x}{a}\right)^n + \left( \frac{y}{b}\right)^n = 1\) with \(\frac{a}{b} = \frac{9}{7}\) and \(n = e\). Use a CAS to find an approximation of the area of the parking garage in the case \(a = 900\) yards, \(b = 700\) yards, and \(n = 2.72\) yards.
[Hide Solution]
\(A(R) \simeq 83,999.2\)
Chapter Review Exercises
True or False? Justify your answer with a proof or a counterexample.
\[\int_a^b \int_c^d f(x,y) \, dy \, dx = \int_c^d \int_a^b f(x,y) \, dy \, dx \nonumber \]
Fubini’s theorem can be extended to three dimensions, as long as \(f\) is continuous in all variables.
[Hide solution]
True.
The integral \[\int_0^{2\pi} \int_0^1 \int_0^1 dz \, dr \, d\theta \nonumber \] represents the volume of a right cone.
The Jacobian of the transformation for \(x = u^2 - 2v, \, y = 3v - 2uv\) is given by \(-4u^2 + 6u + 4v\).
[Hide Solution]
False.
Evaluate the following integrals.
\[\iint_R (5x^3y^2 - y^2) \, dA, \, R = \{(x,y)|0 \leq x \leq 2, \, 1 \leq y \leq 4\} \nonumber \]
\[\iint_D \frac{y}{3x^2 + 1} dA, \, D = \{(x,y) |0 \leq x \leq 1, \, -x \leq y \leq x\} \nonumber \]
[Hide Solution]
\(0\)
\[\iint_D \sin (x^2 + y^2) dA \nonumber \] where \(D\) is a disk of radius \(2\) centered at the origin \[\int_0^1 \int_0^1 xye^{x^2} dx \, dy \nonumber \]
[Hide Solution]
\(\frac{1}{4}\)
\[\int_{-1}^1 \int_0^z \int_0^{x-z} 6dy \, dx \, dz \nonumber \]
\[\iiint_R 3y \, dV, \nonumber \] where \(R = \{(x,y,z) |0 \leq x \leq 1, \, 0 \leq y \leq x, \, 0 \leq z \leq \sqrt{9 - y^2}\}\)
[Hide Solution]
\(1.475\)
\[\int_0^2 \int_0^{2\pi} \int_r^1 r \, dz \, d\theta \, dr \nonumber \]
\[\int_0^{2\pi} \int_0^{\pi/2} \int_1^3 \rho^2 \, \sin(\varphi) d\rho \, d\varphi, \, d\theta \nonumber \]
[Hide Solution]
\(\frac{52}{3} \pi\)
\[\int_0^1 \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{-\sqrt{1-x^2-y^2}}^{\sqrt{1-x^2-y^2}} dz \, dy \, sx \nonumber \]
For the following problems, find the specified area or volume.
The area of region enclosed by one petal of \(r = \cos (4\theta)\).
[Hide Solution]
\(\frac{\pi}{16}\)
The volume of the solid that lies between the paraboloid \(z = 2x^2 + 2y^2\) and the plane \(z = 8\).
The volume of the solid bounded by the cylinder \(x^2 + y^2 = 16\) and from \(z = 1\) to \(z + x = 2\).
[Hide Solution]
\(93.291\)
The volume of the intersection between two spheres of radius 1, the top whose center is \((0,0,0.25)\) and the bottom, which is centered at \((0,0,0)\).
For the following problems, find the center of mass of the region.
\(\rho(x,y) = xy\) on the circle with radius \(1\) in the first quadrant only.
[Hide Solution]
\(\left(\frac{8}{15}, \frac{8}{15}\right)\)
\(\rho(x,y) = (y + 1) \sqrt{x}\) in the region bounded by \(y = e^x, \, y = 0\), and \(x = 1\).
\(\rho(x,y,z) = z\) on the inverted cone with radius \(2\) and height \(2\).
\(\left(0,0,\frac{8}{5}\right)\)
The volume an ice cream cone that is given by the solid above \(z = \sqrt{(x^2 + y^2)}\) and below \(z^2 + x^2 + y^2 = z\).
The following problems examine Mount Holly in the state of Michigan. Mount Holly is a landfill that was converted into a ski resort. The shape of Mount Holly can be approximated by a right circular cone of height \(1100\) ft and radius \(6000\) ft.
If the compacted trash used to build Mount Holly on average has a density \(400 \, lb/ft^3\), find the amount of work required to build the mountain.
[Hide Solution]
\(1.452 \pi \times 10^{15} \) ft-lb
In reality, it is very likely that the trash at the bottom of Mount Holly has become more compacted with all the weight of the above trash. Consider a density function with respect to height: the density at the top of the mountain is still density \(400 \, lb/ft^3\) and the density increases. Every \(100\) feet deeper, the density doubles. What is the total weight of Mount Holly?
The following problems consider the temperature and density of Earth’s layers.
[T] The temperature of Earth’s layers is exhibited in the table below. Use your calculator to fit a polynomial of degree \(3\) to the temperature along the radius of the Earth. Then find the average temperature of Earth. (Hint: begin at \(0\) in the inner core and increase outward toward the surface)
| Layer | Depth from center (km) | Temperature \(^oC\) |
| Rocky Crust | 0 to 40 | 0 |
| Upper Mantle | 40 to 150 | 870 |
| Mantle | 400 to 650 | 870 |
| Inner Mantel | 650 to 2700 | 870 |
| Molten Outer Core | 2890 to 5150 | 4300 |
| Inner Core | 5150 to 6378 | 7200 |
Source: http://www.enchantedlearning.com/sub...h/Inside.shtml
[Hide Solution]
\(y = -1.238 \times 10^{-7} x^3 + 0.001196 x^2 - 3.666x + 7208\); average temperature approximately \(2800 ^oC\)
[T] The density of Earth’s layers is displayed in the table below. Using your calculator or a computer program, find the best-fit quadratic equation to the density. Using this equation, find the total mass of Earth.
| Layer | Depth from center (km) | Density \((g/cm^3)\) |
| Inner Core | 0 | 12.95 |
| Outer Core | 1228 | 11.05 |
| Mantle | 3488 | 5.00 |
| Upper Mantle | 6338 | 3.90 |
| Crust | 6378 | 2.55 |
Source: http://hyperphysics.phy-astr.gsu.edu...rthstruct.html
The following problems concern the Theorem of Pappus (see Moments and Centers of Mass for a refresher), a method for calculating volume using centroids. Assuming a region \(R\), when you revolve around the \(x\)-axis the volume is given by \(V_x = 2\pi A \bar{y}\), and when you revolve around the \(y\)-axis the volume is given by \(V_y = 2\pi A \bar{x}\), where \(A\) is the area of \(R\). Consider the region bounded by \(x^2 + y^2 = 1\) and above \(y = x + 1\).
Find the volume when you revolve the region around the \(x\)-axis.
[Hide Solution]
\(\frac{\pi}{3}\)
Find the volume when you revolve the region around the \(y\)-axis.
Glossary
- Jacobian
-
the Jacobian \(J (u,v)\) in two variables is a \(2 \times 2\) determinant:
\[J(u,v) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \end{vmatrix}; \nonumber \]
the Jacobian \(J (u,v,w)\) in three variables is a \(3 \times 3\) determinant:
\[J(u,v,w) = \begin{vmatrix} \frac{\partial x}{\partial u} \frac{\partial y}{\partial u} \frac{\partial z}{\partial u} \nonumber \\ \frac{\partial x}{\partial v} \frac{\partial y}{\partial v} \frac{\partial z}{\partial v} \nonumber \\ \frac{\partial x}{\partial w} \frac{\partial y}{\partial w} \frac{\partial z}{\partial w}\end{vmatrix} \nonumber \]
- one-to-one transformation
- a transformation \(T : G \rightarrow R\) defined as \(T(u,v) = (x,y)\) is said to be one-to-one if no two points map to the same image point
- planar transformation
- a function \(T\) that transforms a region \(G\) in one plane into a region \(R\) in another plane by a change of variables
- transformation
- a function that transforms a region GG in one plane into a region RR in another plane by a change of variables



Jacobianos
Recordemos que mencionamos cerca del inicio de esta sección que cada una de las funciones componentes debe tener primeras derivadas parciales continuas, lo que significa que\(g_u, g_v, h_u\) y\(h_v\) existir y también son continuas. Una transformación que tiene esta propiedad se denomina\(C^1\) transformación (aquí\(C\) denota continua). Dejar\(T(u,v) = (g(u,v), \, h(u,v))\), dónde\(x = g(u,v)\) y\(y = h(u,v)\) ser una\(C^1\) transformación uno-a-uno. Queremos ver cómo transforma una pequeña región rectangular\(S, \, \Delta u\) unidades por\(\Delta v\) unidades, en el\(uv\) plano -plano (Figura\(\PageIndex{4}\)).
Desde\(x = g(u,v)\) y\(y = h(u,v)\), tenemos el vector\(r(u,v) = g(u,v)i + h(u,v)j\) de posición de la imagen del punto\((u,v)\). Supongamos que\((u_0,v_0)\) es la coordenada del punto en la esquina inferior izquierda que mapeó a\((x_0,y_0) = T(u_0,v_0)\) La línea se\(v = v_0\) mapea a la curva de imagen con función de vector\(r(u,v_0)\), y el vector tangente\((x_0,y_0)\) a la curva de imagen es
\[r_u = g_u (u_0,v_0)i + h_v (u_0,v_0)j = \frac{\partial x}{\partial u}i + \frac{\partial y}{\partial u}j. \nonumber \]
De manera similar, la línea se\(u = u_0\) mapea a la curva de imagen con la función de vector\(r(u_0,v)\), y el vector tangente\((x_0,y_0)\) a la curva de imagen es
\[r_v = g_v (u_0,v_0)i + h_u (u_0,v_0)j = \frac{\partial x}{\partial v}i + \frac{\partial y}{\partial v}j. \nonumber \]
Ahora, tenga en cuenta que
\[r_u = \lim_{\Delta u \rightarrow 0} \frac{r (u_0 + \Delta u, v_0) - r ( u_0,v_0)}{\Delta u}\, so \, r (u_0 + \Delta u,v_0) - r(u_0,v_0) \approx \Delta u r_u. \nonumber \]
Del mismo modo,
\[r_v = \lim_{\Delta v \rightarrow 0} \frac{r (u_0,v_0 + \Delta v) - r ( u_0,v_0)}{\Delta v}\, so \, r (u_0,v_0 + \Delta v) - r(u_0,v_0) \approx \Delta v r_v. \nonumber \]
Esto nos permite estimar el área\(\Delta A\) de la imagen\(R\) encontrando el área del paralelogramo formado por los lados\(\Delta vr_v\) y\(\Delta ur_u\). Al usar el producto cruzado de estos dos vectores agregando el k ésimo componente como\(0\), el área\(\Delta A\) de la imagen\(R\) (consulte El producto cruzado) es aproximadamente\(|\Delta ur_u \times \Delta v r_v| = |r_u \times r_v|\Delta u \Delta v\). En forma determinante, el producto cruzado es
\[r_u \times r_v = \begin{vmatrix} i & j & k \\ \frac{\partial x}{\partial u} & \frac{\partial y}{\partial u} & 0 \\ \frac{\partial x}{\partial v} & \frac{\partial y}{\partial v} & 0 \end{vmatrix} = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} k = \left(\frac{\partial x}{\partial u} \frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right)k \nonumber \]
Ya\(|k| = 1,\) que tenemos
\(\Delta A \approx |r_u \times r_v| \Delta u \Delta v = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right) \Delta u \Delta v.\)
Definición: Jacobian
El jacobiano de la\(C^1\) transformación\(T(u,v) = (g(u,v), \, h(u,v))\) se denota por\(J(u,v)\) y se define por el\(2 \times 2\) determinante
\[J(u,v) = \left|\frac{\partial (x,y)}{\partial (u,v)} \right| = \begin{vmatrix} \dfrac{\partial x}{\partial u} & \dfrac{\partial y}{\partial u} \\ \dfrac{\partial x}{\partial v} & \dfrac{\partial y}{\partial v} \end{vmatrix} = \left( \frac{\partial x}{\partial u}\frac{\partial y}{\partial v} - \frac{\partial x}{\partial v} \frac{\partial y}{\partial u}\right). \nonumber \]