1.1: Funciones y modelos lineales

Comenzaremos este capítulo con una revisión de las funciones lineales. En los negocios hay bastantes ejemplos de ecuaciones lineales. Los ejemplos incluyen funciones de oferta y demanda. Hay algunos conceptos estándar relacionados con las líneas que revisaremos, incluyendo la pendiente.

Siguiendo las convenciones de la microeconomía, a menudo usaremos las variables p y q, para precio y cantidad, en lugar de x e y, también seguiremos las convenciones de la economía para tratar la cantidad como variable independiente. (El eje q será el eje horizontal. Una búsqueda rápida en la web para el equilibrio de oferta y demanda le convencerá de este uso estándar).

Ecuaciones de una línea

De cursos anteriores, como álgebra universitaria, recordarás que las líneas se pueden escribir en varias formas diferentes. Si se nos da la pendiente y la\(y\) -intercepción, la forma de intercepción de pendiente será la ecuación de elección. Si se nos da un punto y una pendiente, podría ser más rápido si usamos la forma de punto-pendiente de una línea.

\[y=m x+b \nonumber \]

la forma pendiente-intercepción de una línea

\[y-y_0=m(x-x_0) \nonumber \]

la forma punto-pendiente de una línea

En un entorno empresarial, es probable que utilicemos\(q\) en lugar de\(x\) y\(p\) en lugar de\(y\). Con esta notación estas ecuaciones estándar de una línea se convierten en:

\[p=mq+b \nonumber \]

la forma pendiente-intercepción de una línea

\[p-p_0=m(q-q_0) \nonumber \]

la forma punto-pendiente de una línea

Ejemplo 1.1.1

Las ecuaciones de oferta y demanda a menudo se modelan mediante ecuaciones lineales. La función de oferta es una línea con pendiente positiva, y la función de demanda es una línea con pendiente negativa.

Solución

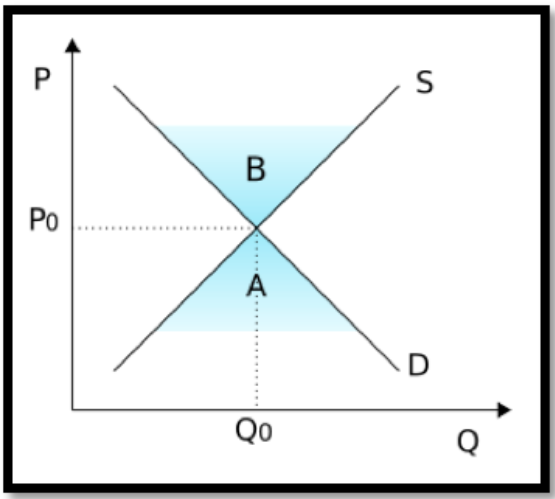
\(Figure \text { } 1.1.2.\)La intersección de una curva de oferta y demanda

El eje vertical muestra el precio, el eje horizontal muestra la cantidad. Tanto la oferta (S) como la demanda (D) son funciones lineales. En este diagrama 'B' denota un excedente de oferta, y 'A' denota un excedente de demanda.

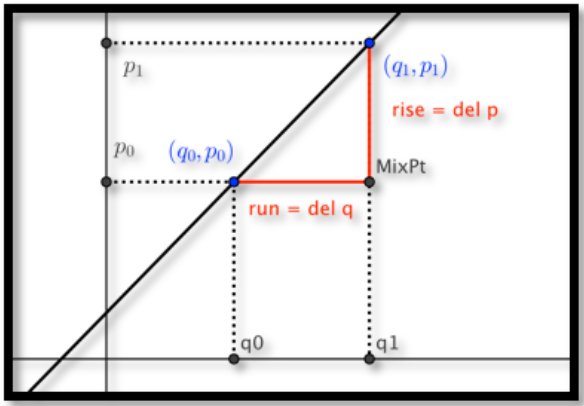
Recordemos, que la pendiente de una línea a través de los puntos\(P_0=(q_0,p_0)\) y\(P_1=(q_1,p_1)\) viene dada por:

\[ m=\frac{\text{rise}}{\text{run}}=\frac{(p_1-p_0)}{(q_1-q_0 )} \nonumber \]

Hay otras dos formas de una línea que a veces se utilizan. La forma general de una línea es una notación estándar utilizada en matemáticas. La forma de 2 puntos de una línea es muy útil en aquellas situaciones en las que no se nos da una pendiente, sino que se nos da información sobre dos puntos que se encuentran en la línea.

\[a x+b y+c=0 \nonumber \]

La forma general de una línea

\[y-y_0=\frac{y_1-y_0}{x_1-x_0 }(x-x_0) \nonumber \]

La forma de 2 puntos de una línea

Como anteriormente, en la configuración de este curso podemos estar usando\(p\) (precio) y\(q\) (cantidad) como nuestras variables. Esto daría como resultado ecuaciones que se ven de la siguiente manera:

\[a q+b p+c=0 \nonumber \]

La forma general de una línea

\[p-p_0=\frac{p_1-p_0}{q_1-q_0 }(q-q_0) \nonumber \]

La forma de 2 puntos de una línea

Ejemplo 1.1.3: Encontrar cuatro versiones de una línea.

Encontramos que podemos vender 150 widgets al día si los vendemos a $10. Si elevamos el precio a $15, solo podemos vender 110 widgets al día. Supongamos que existe una relación lineal entre precio y cantidad vendida. Encuentra la ecuación de la línea en las cuatro formas.

Solución

Escribiendo esto usando nuestras variables\(p\) (precio) y\(q\) (cantidad de widgets) vemos que cuando\(p = 10\text{,}\)\(q = 150\) y cuando\(p = 15\text{,}\)\(q = 110\text{.}\) los Puntos se dan (generalmente) como\((q,p)\text{,}\) así esto significa que tenemos dos puntos\((150,10)\) y\((110,15)\) en la línea. Siempre necesitamos encontrar la pendiente de la línea, y en este caso

\[ m= \frac{15-10}{110-150}= \frac{5}{-40}= \frac{-1}{8}\text{.} \nonumber \]

Se nos dan dos puntos, por lo que la forma de 2 puntos de la línea debería ser la fórmula más fácil de encontrar:

\[ p-p_0=\frac{p_1-p_0}{q_1-q_0 }(q-q_0)\text{.} \nonumber \]

Acabamos de encontrar la pendiente y solo necesitamos escoger un punto\((p_0,q_0)\) para terminar con el problema. (Recordemos que\(p\) y\(q\) son las variables, así que queremos dejarlas como están.) En este caso vamos a escoger\((p_0,q_0)= (150,10)\text{.}\) Luego obtenemos esta versión simplificada, que es también la forma de punto-pendiente de esta línea.

\[ p-10=\frac{-1}{8}(q-150)\text{.} \nonumber \]

Desde aquí podemos encontrar muy fácilmente la forma de intercepción de pendiente por algún álgebra directa:\(p-10=\frac{-1}{8}(q-150)\) implica que

\[ p=\frac{-1}{8} (q-150)+10= \frac{-1}{8} q+ \frac{150}{8}+10= \frac{-1}{8} q+\frac{230}{8}\text{.} \nonumber \]

Y finalmente la forma general será otro ejercicio de álgebra. Despejamos las fracciones y ponemos todo de un lado.

\[ 8p+q-230=0\text{.} \nonumber \]

Ejemplo 1.1.3: Encontrar una línea a partir de dos puntos

Supongamos que existe una relación lineal costo-cantidad en la producción de widgets. Hay un costo fijo de $400. También hay un costo por unidad de $11.

1. Encuentra la ecuación de la línea.
2. Encuentra el costo de hacer 200 widgets.

Solución

1. Tenemos un punto de la forma (cantidad, costo) a (0, 400) del costo fijo. Este punto pasa a ser una intercepción. La pendiente de la línea es\(m=11/1=11\text{.}\) Dejaremos\(C\) reposar por Costo y\(q\) representaremos cantidad. La fórmula general para una línea con estas variables tendrá la forma\[ C=m q+b. \nonumber \nonumber \] En este ejemplo\(m = 11\) y de\(b = 400\text{,}\) ahí la ecuación de la línea es\[ C=11 q+400 \nonumber \]
2. Usando la ecuación forma parte a) vemos que el costo de producir 200 widgets es\[ C=11 (200)+400=\$2,600 \nonumber \nonumber \]

Ejemplo 1.1.5: Una función no lineal

A Sarah se le paga $500 por trabajar hasta 40 horas semanales. Por trabajo más allá de 40 horas semanales se le paga $18/hora.

1. Encuentra la ecuación de la línea.
2. ¿Cuánto se le paga si trabaja 56 horas en una semana?
3. ¿Qué le paga por trabajar 30 horas en una semana?

Solución

1. Para este ejemplo usaremos “variables de diseñador”. La salida será Pagar, y la variable de entrada —el número de horas trabajadas— será hrs. Nos dicen que Pagar = 500 cuando hrs = 40. La pendiente de la línea de trabajo más allá de las 40 horas es\(m=18\text{.}\) Otra forma de pensar en esto es decir que hay un Pago fijo de $500 y un Pago variable por cualquier hora superior a 40: es decir (hrs - 40). Así, la ecuación de la línea, según la forma punto-pendiente es\[ \text{Pay} = \text{variable pay} + \text{Fixed pay}\text{.} \nonumber \nonumber \] Esto nos da\[ Pay=m(hrs-40)+500=18*(hrs-40)+500\text{.} \nonumber \]
2. El pago por trabajar 56 horas es de 18 (56-40) +500=$788.
3. El pago por trabajar 30 horas es de $500. Esta es una pregunta engañosa que forma parte del problema. A partir del texto del problema, el modelo lineal sólo funciona para horas extras, con una tarifa plana que se aplica a menos de 40 horas semanales. Comentario: La función debe escribirse como una función definida por partes.

Esta pregunta tiene que ver con la función\(f\) definida por

\[ \operatorname{Pay}=\begin{cases} 500 & \text{hrs}\le 40\\ 18*(hrs-40)+500 & \text{hrs}>40\\ \end{cases} \nonumber \]

Puede ser útil a la hora de escribir informes tener variables que transmitan algún significado. Podríamos haber usado\(y\) para\(\operatorname{Pay}\text{,}\) y\(x\) para\(\text{hrs}\text{,}\) pero usar las variables mucho más fáciles de interpretar llamadas Pay y hrs ayuda a la hora de usar las fórmulas.

Ejercicios 1.1.2 Ejercicios 1.1 Funciones lineales y modelos

Para problemas 1-6, dados dos puntos en el\((q,p)\) plano y un valor\(q_0\text{:}\)

1. Encuentra la pendiente de la línea determinada por los puntos.
2. Dar la ecuación de la línea determinada por los puntos.
3. Dar el valor de\(p\) predicho para\(q_0\) por la línea.

Ejercicio 1:

Puntos\((2,5)\) y\((6,17)\text{,}\) con\(q_0=4\text{.}\)

Pista.

Encuentra el talud y usa la forma de talud puntual

Contestar

Primero encuentra la pendiente:\(m= \frac{\text{change in }p}{\text{change in }q} = \frac{17-5}{6-2}=\frac{12}{4}=3\)

A continuación encontramos la ecuación de la línea. Hay varias formas de hacerlo y a continuación se describen dos métodos.

• Método 1: usar la ecuación punto-pendiente:\(p-p_0=m (q-q_0)\text{.}\) Podemos elegir cualquiera de los puntos, así que en este caso encontraremos la línea usando el punto\((q_0,p_0 )=(2,5)\text{.}\) Esto da la ecuación\(p-5=3 (q-2)\text{.}\)

  Reescribe esto como\(p=3q-1\)

• Método 2: usar la ecuación de pendiente- interceptar\(p=m q+b\text{.}\) Usar\((q,p)=(2,5)\)\(m = 3\) y resolver para\(b\text{:}\)\(5=3 (2)+b\text{.}\) Y resolviendo para\(b\) tenemos eso\(b= -1\text{,}\) y por lo tanto\(p=3q-1\)

Evaluar en el punto dado. \(p(4)=3*4-1=11\)

Ejercicio 2:

Puntos\((5,7)\) y\((10,7)\text{,}\) con\(q_0=20\text{.}\)

Ejercicio 3:

Puntos\((20,10)\) y\((40,5)\text{,}\) con\(q_0=12\text{.}\)

Contestar

Así como en el problema 1 encontramos la pendiente y luego encontramos la ecuación de la línea.

Primero encuentra la pendiente:\(m= \frac{\text{change in }p}{\text{change in }q} = \frac{5-10}{40-20}=-\frac{5}{20}=-\frac{1}{4}\)

Usando\(p=m (q-q_0)+p_0\) con\((q_0,p_0 )=(20, 10)\) y\(m = -\frac{1}{4}\text{,}\) obtenemos\(p=-\frac{1}{4}(q-20)+10\text{.}\) Resolviendo\(p\) porque obtenemos\(p =-\frac{1}{4}q+15\)

Evaluar en el punto dado. \(p(12)=-\frac{1}{4}(12)+15=12\)

Ejercicio 4:

Puntos\((5,62)\) y\((115,783)\text{,}\) con\(q_0=415\text{.}\)

Ejercicio 5:

Puntos\((273,578)\) y\((412,6)\text{,}\) con\(q_0=309\text{.}\)

Contestar

Así como en el problema 1 encontramos la pendiente y luego encontramos la ecuación de la línea.

Primero encuentra la pendiente:\(m= \frac{\text{change in }p}{\text{change in }q} = \frac{578-6}{273-412}=-\frac{572}{139}\)

Usando\(p=m (q-q_0)+p_0\) con\((q_0,p_0 )=(412, 6)\) y\(m = -\frac{572}{139}\text{,}\) obtenemos\(p=-\frac{572}{139}(q-412)+6\text{.}\) (Podemos combinar los términos constantes — el\(6\) y el\(-\frac{572}{139}*(-412)\text{,}\) pero dejar la ecuación en esta forma es aceptable.)

Evaluar en el punto dado. \(p(309)=-\frac{572}{139}(309-412)+6 =-\frac{572}{139}(-103)+6=429\frac{119}{139}\)

Ejercicio 6:

Puntos\((509,17)\) y\((211,132)\text{,}\) con\(q_0=4\text{.}\)

• Para problemas 7-12, comience con la información dada:

1. Dar la ecuación de la línea determinada por esa información.
2. Usando la línea, dar el valor predicho de\(p\) para el\(q_0\text{.}\)
3. Dar el valor\(q\) para el cual el valor predicho de\(p\) es\(0\text{.}\)

Ejercicio 7:

Una pendiente de\(3\text{,}\) paso\((6,3)\text{,}\) con\(q_0=4\text{.}\)

Contestar

Usando\(p=m q+b\text{,}\) obtenemos\(3=3 (6)+b\text{,}\) así\(b= -15\) y la ecuación de la línea es\(p=3 q-15\)

Si\(q_0=4\text{,}\) entonces\(p=3 q-15=3(4)-15= -3\)

El valor predicho de\(p\) es\(0\text{,}\) cuando\(0=3 q-15\text{.}\) Resolver para\(q\) obtenemos\(q=5\text{.}\) [Comentario: en la parte a) podríamos haber usado la pendiente de punto para también.]

Ejercicio 8:

Una pendiente de\(-2\text{,}\) paso\((2,-5)\text{,}\) con\(q_0=3\text{.}\)

Ejercicio 9:

Una pendiente de\(12.7\text{,}\) paso\((22,183)\text{,}\) con\(q_0=46\text{.}\)

Contestar

Usando\(p=m (q-q_0 )+p_0\) obtenemos\(p=12.7 (q-22)+183\text{.}\)

Cuando\(q_0=46\text{,}\) lleguemos eso\(p=12.7 (46-22)+183=12.7(24)+183\text{.}\) Y por lo tanto\(p=487.8\)

El valor predicho de\(p\) es\(0\text{,}\) cuando\(0=183+12.7 (q-22)\text{.}\) Resolver para\(q\) obtenemos:\(12.7 (q-22)= -183\) Esto implica\((q-22)= \frac{-183}{12.7}\text{.}\) Por lo tanto,

\[ q=22 -\frac{183}{12.7}=7.59\text{.} \nonumber \]

Ejercicio 10:

Una pendiente de\(-0.23\text{,}\) paso\((7.6,19.7)\text{,}\) con\(q_0=59.6\text{.}\)

Ejercicio 11:

Una pendiente de 0, pasando\((12.3,9.8)\text{,}\) por\(q_0=74\text{.}\)

Contestar

Usando\(p=m (q-q_0 )+p_0\) obtenemos\(p=0 (q-12.3)+9.8\) o\(p=9.8\text{.}\)

Cuando\(q_0=74\text{,}\) lleguemos eso\(p=9.8\text{.}\) (Esta es una función constante, y la salida va a ser\(9.8\) sin importar qué valor de\(q\) conectemos.)

El valor predicho de nunca\(p\) es\(0\text{,}\) porque el valor predicho de p es siempre 9.8.

Ejercicio 12:

Agrega texto de ejercicios aquí.

Contestar

Una pendiente que no está definida, pasando\((6,3)\text{,}\) explicando por qué la parte b no tendría sentido.

• Para los problemas 13-18, comience con la ecuación dada:

1. Dar la pendiente de la línea o decir que la pendiente es indefinida.
2. Dar las intercepciones de la línea con los ejes.
3. Dar dos puntos que están en la línea pero no en los ejes.

Ejercicio 13:

\(3 p+2 q=6\text{.}\)

Contestar

Resuelva para\(p\) que podamos leer la pendiente más fácilmente:\(p= -2/3 q+2\text{.}\) De ahí que la pendiente sea\(m= -2/3\)

Para obtener la\(p\) -intercepción establecemos\(q=0\text{,}\) así que\(3 p=6\text{,}\) y obtenemos\(p=2\) Para obtener la\(q\) -intercepción establecemos\(p=0\text{,}\) para que\(2q=6\text{,}\) y obtengamos\(q=3\)

Podemos escoger cualquiera de dos valores para\(q\) (excepto\(0\) y\(3\) porque esos son interceptos), así que arbitrariamente elegir algunos valores: decir\(q=1\) y\(q=-1\text{.}\) Si\(q=1\text{,}\) entonces\(3 p+2=6\text{,}\) y por lo tanto\(p=4/3\) así el punto sería\((q,p)=(1,4/3)\) Si\(q=-1\text{,}\) entonces\(3 p-2=6\text{,}\) y por lo tanto \(p=8/3\)por lo que el punto sería\((q,p)=(-1,8/3 )\)

Ejercicio 14:

\(7 p-4 q+14=0\text{.}\)

Ejercicio 15:

\(y=5\text{.}\)

Contestar

La pendiente es\(0\)

La intercepción y es No\(y = 5\text{.}\) hay\(x\) -intercepción

No importa lo que\(x\) escojamos el\(y\) valor siempre será\(5\text{.}\) Así que podemos escoger cualquiera de dos valores de\(x\) (no\(0\) para evitar la intercepción). Por ejemplo\((x,y)=(-20,5)\text{,}\)\((x,y)=(-2,5)\text{,}\)\((x,y)=(7,5)\text{,}\), etc son todos los puntos en la línea.

Ejercicio 16:

\(x=3\text{.}\)

Ejercicio 17:

\(y=4(x-3)+9\text{.}\)

Contestar

La pendiente es\(4\)

Para obtener la\(y\) -intercepción nos fijamos de\(y=0\text{,}\) manera que\(y=4(-3)+9=-3\text{,}\)

Para obtener la\(x\) -intercepción nos fijamos para\(y=0\text{,}\) que\(0=4(x-3)+9\text{.}\) Resolver para\(x\) y obtengamos\(x-3=-\frac{9}{4}\) y\(x=3-\frac{9}{4}=\frac{3}{4}\)

Evitando las intercepciones podemos\(x\) optar por ser cualquier número que no sea\(x = 0\) y\(x=3/4\text{.}\) podemos buscar buenos valores de\(x\) que hagan que la aritmética salga bien: por ejemplo elegir\(x=3\) y\(x=4\text{.}\) cuándo\(x=3\text{,}\)\(y=9\text{,}\) y obtenemos el punto\((x,y)=(3,9)\text{.}\) Cuándo \(x=4\text{,}\)\(y=13\text{,}\)y conseguimos el punto\((x,y)=(4,13)\text{.}\)

Ejercicio 18:

\(112 p+257 q=4783\text{.}\)

Ejercicio 19:

Supongamos que la relación entre precio y cantidad de widgets vendidos es lineal. Cuando el precio es de 23 dólares, podemos vender 4783 widgets. Si elevamos el precio a 27 dólares, solo podemos vender 4295 widgets. Encuentra la ecuación de la línea.

Contestar

La información nos dice que tenemos dos puntos:\((q,p)=(4783,23)\) y\((q,p)=(4295,27)\text{.}\) (Tenga en cuenta que en los negocios la cantidad\(q\) suele ser la entrada y el precio\(p\) suele ser la salida.)

A continuación necesitamos la pendiente:\(m= (27-23)/(4295-4783)=4/(-488)=-1/122\)

Usando\(p-p_0=m (q-q_0 )\) obtenemos\(p-23=-1/122 (q-4783)\text{.}\) Podemos reescribir este último como\(p=23-1/122 (q-4783)\text{.}\)

Ejercicio 20:

Supongamos que la relación entre precio y cantidad de kits de gizmo que podemos comprar es lineal. Cuando el precio es de $15, podemos comprar 6000 kits de gizmo. Si bajamos el precio pagaremos a $13, solo podremos comprar 4500 kits. Encuentra la ecuación de la línea.