1.2: Funciones en el ámbito empresarial

Última actualización
Guardar como PDF

Page ID: 115965

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

No todas las funciones que encontramos en un entorno empresarial son lineales. Hay varias otras familias de funciones con las que debemos (re) familiarizarnos. Estos modelos incluyen:

Funciones cuadráticas
Funciones exponenciales
Funciones logísticas
Funciones normales de distribución
Funciones sinusoidales

Funciones Cuadráticas.

Las funciones cuadráticas deben ser muy familiares a partir de cursos previos de matemáticas. Son de la forma$y=a x^2+b x+c\text{.}$ Estas son nuestras paráolas estándar.

En los negocios nos encontramos con ecuaciones cuadráticas cuando estudiamos las funciones de ingresos y ganancias. Recuerda de tu curso de economía que:

\[ \revenue=\price*\quantity=p*q \nonumber \]

En algunos de los modelos vamos a investigar más adelante en el curso el precio será una función lineal. Supondremos$\price=m q+b\text{.}$ Esto implica que

\[ \revenue=(m q+b)*q=m q^2+b q \nonumber \]

Si$m > 0\text{,}$ entonces la función de ingresos se verá como una parábola que se abre. Si$m \lt 0,$ entonces la función de ingresos se verá como una parábola que se abre hacia abajo.

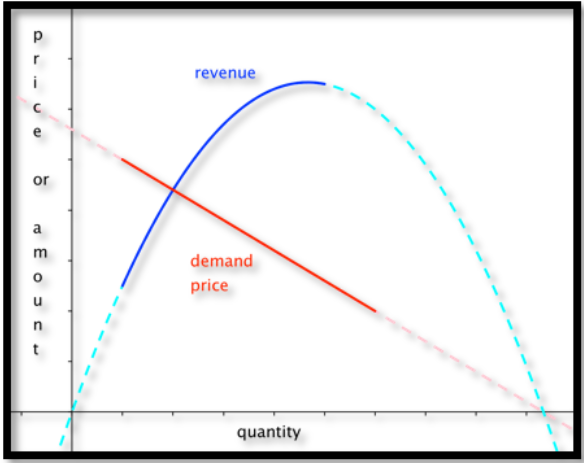
$clipboard_ea70c3454d2e00cbad4206f83f761ba91.png$

$Figure \text { } 1.2.1.$Una función cuadrática

Para un modelo cuadrático muchas veces nos interesan mucho las coordenadas del vértice, y cualquier posible ceros. Para la ecuación general$y=a x^2+b x+c$ el signo del coeficiente de$x^2\text{,}$$a\text{,}$ determinará si tenemos un máximo o un mínimo. Si$a$ es positivo, la parábola se abre y el vértice será mínimo. Si$a$ es negativo, la parábola se abre hacia abajo y el vértice será máximo.

Recordemos que podemos encontrar los ceros de una cuadrática usando la ecuación cuadrática.

\[ \text{roots or zeroes} = \frac{-b\pm\sqrt{b^2-4ac}}{2a}\text{.} \nonumber \]

A partir de esta ecuación vemos que el vértice debe ubicarse en$x= -b/(2a.)\text{.}$ El discriminante (el término debajo del signo radical determina si hay 0, 1, o 2 raíces.

Si$b^2-4ac>0\text{,}$ entonces hay 2 raíces.
Si$b^2-4ac=0\text{,}$ entonces hay 1 raíz (el vértice tocará el eje)
Si$b^2-4ac\lt 0\text{,}$ entonces no hay raíces. Esto significa que toda la gráfica debe estar por encima del$x$ eje -axis ($a > 0$) o debajo del$x$ -axis ($a \lt 0$).

A veces podemos necesitar polinomios más generales en un modelo, con una ecuación de la forma$f(x)=a_n x^n+\cdots+a_1 x+a_0\text{.}$ En tales casos recordamos que el número de puntos de inflexión de la gráfica no puede ser mayor que$n-1\text{.}$

Funciones exponenciales.

El modelo exponencial, con una ecuación de la forma$f(t)=p*e^t\text{.}$ A veces la función exponencial$e^t$ es denotada por$exp(t)\text{.}$ Excel utilizará este formato, por lo que vale la pena mirar la notación en este caso. $f(t)=p*e^{rt}$también se puede escribir como$f(t)=p*exp(r t)$

A los libros de matemáticas (y Excel) les gusta usar una base de$e$ porque facilita las matemáticas cuando hacemos cálculo, por lo que la ecuación se escribe como$f(t)=p*e^{rt}$ o$f(t)=p*exp(r t)\text{.}$ Sin embargo, en las aplicaciones del mundo real tendemos a usar$A=pR^t$ y hacer la ecuación$f(t)=p*R^t\text{.}$ (Se advierte al lector que$R=e^r$ y ambos$R$ y$r$ se les conoce como la tasa. Tendrás que usar el contexto para diferenciarlos.)

Las funciones exponenciales se utilizan para el crecimiento proporcional o decaimiento. En los negocios, el interés compuesto se da como una función exponencial. En particular, si$P$ es el principal y$r$ es la tasa de interés “compuesta continuamente” (expresada como decimal), entonces la cantidad$A$ después del tiempo$t$ viene dada por$A=P e^rt\text{.}$ La relación (en general) entre un valor futuro (FV) y el valor presente (PV) dado una tasa de interés$r$ por periodo,$t$ siendo el número de periodos compuestos viene dado por:

\[ \FutureValue: FV=PV*(1+r)^t \nonumber \]

También es útil para determinar un valor razonable hoy de un pago futuro prometido. El signo de la tasa determinará si la gráfica se vuelve hacia arriba o hacia abajo.

Al modelar el comportamiento del mundo real, a menudo conocemos algunas características especiales del problema. Por ejemplo, podemos saber que nuestro valor actual es de $2,000 y que nos gustaría que el valor futuro fuera de 10,000 dólares después de 10 años. La pregunta sería ¿qué función describiría tal modelo? Un método comúnmente utilizado para resolver tal problema es enchufar los valores que se nos dan y ver si podemos determinar cuáles deben ser las cantidades restantes. Sabemos que$FV=PV*(1+r)^t\text{.}$ La información extra nos dice PV = 2000, y cuando t = 10 sabemos que$FV=2000*(1+r)^{10}=10,000\text{.}$ Esta es suficiente información para resolver para r. Dividir ambos lados por 2000 muestra que$(1+r)^{10}=5\text{.}$

Para resolver esta ecuación necesitamos reglas de exponentes. Obtenemos$1+r=5^{1⁄10}\text{,}$ y por lo tanto$r= 5^{1/10}-1= 0.1746\text{.}$ Esto significa que para obtener tal crecimiento necesitaríamos una tasa de crecimiento de alrededor del 17.46%. La función modelando que sería el crecimiento$FV=2000*(1.1746)^t\text{.}$ En general podemos configurar ecuaciones y resolver para las cantidades desconocidas.

Funciones Logísticas.

El modelo exponencial asume crecimiento sin fin. Eso es imposible en la mayoría de las situaciones de negocios. En cambio, normalmente hay un punto donde el mercado está saturado. El modelo alternativo dice que la tasa de cambio es proporcional tanto a la cantidad actual como a la distancia desde el valor máximo teórico. A esto se le llama crecimiento logístico. Una fórmula típica para el crecimiento logístico dado un punto de saturación de$r\text{,}$ mercado de tasa de interés$M\text{,}$ y constante a dependiendo del problema es

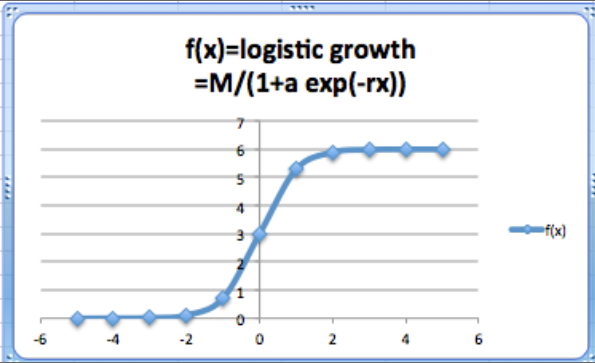
\[ f(x)= \frac{M}{1+a e^{-rx}} \text{.} \nonumber \]

En Excel escribiríamos esta función como: f (x) =M/ (1+a exp (-r x)). Usando Excel es bastante fácil crear una tabla y graficar una función logística.

$clipboard_ea42bafe5821bcb76807c70d8fb87b634.png$

Funciones sinusoidales.

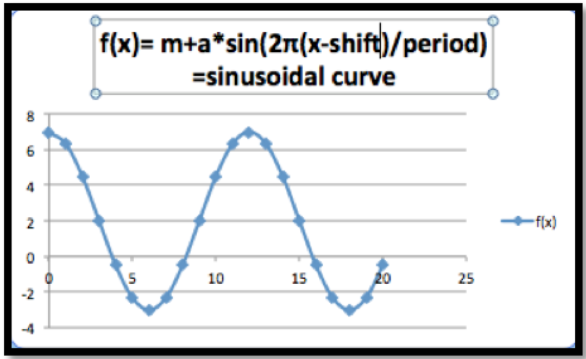
El modelo sinusoidal es para datos que se repiten en un ciclo natural. Ejemplos típicos incluirían la necesidad de combustible para calefacción, electricidad para aire acondicionado y ventas de artículos de temporada como Navidad. La ecuación típica es

\[ f(x)=M+A*\sin(2\pi*(x-\text{shift})/\text{period})\text{,} \nonumber \]

donde la media$M$ es el valor promedio, la amplitud$A$ es la distancia desde la media hasta la máxima, el periodo es el tiempo hasta que se repite el ciclo, y el cambio es donde iniciamos el ciclo para$x=0\text{.}$

Con un cambio apropiado podemos intercambiar las funciones seno y coseno. Las funciones$\sin(x)$ y$\cos(x)$ surgen de la trigonometría.) En este curso, no nos centraremos en las funciones trigonométricas y sus propiedades. Solo nos preocupa tener una función periódica para las variaciones estacionales.

$clipboard_e59f4f20111fc8e046118acfce6ef4b41.png$

Funciones de Distribución Normal.

Se utiliza la distribución normal o curva de campana porque muchas poblaciones siguen una distribución normal en muchas escalas. La ecuación

\[ f(x)=a e^{-\left(\frac{(x-m)}{s}\right)^2} \nonumber \]

parece un poco intimidante, pero podremos usar el poder de una hoja de cálculo para manejarla fácilmente.

En retail, hay varios ejemplos de artículos que siguen una distribución normal. En una tienda que vende zapatos para mujeres por ejemplo, esperaríamos ver que algunas tallas son más frecuentes que otras. Esto sería un factor para determinar qué tamaños tener en stock, y en qué cantidades. El escenario típico en el que vamos a utilizar este modelo de curva es aquel en el que preguntamos qué rango de tamaños necesitamos cubrir para que la población en un área sea lo suficientemente grande como para justificar una tienda especializada.

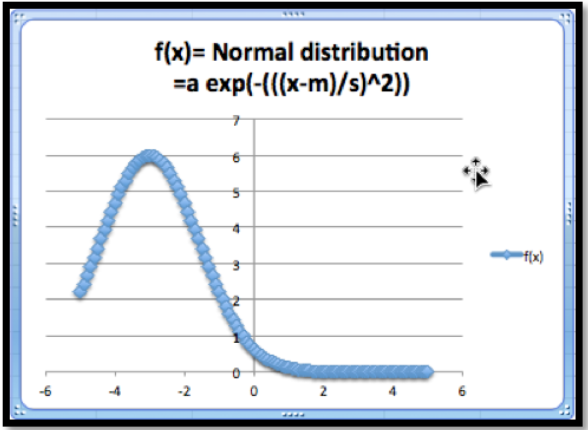
$clipboard_ec04bc6e45eb86821e51be2addf426808.png$

La función de distribución normal tiene ciertas características interesantes. La gráfica muestra un valor máximo. El máximo ocurre cuando$x = m\text{.}$ Y cuando$x = m\text{,}$ sabemos que

\[ f(x)=a e^{\left(\frac{-(m-m)}{s}\right)^2}=a e^0=a*1=a\text{,} \nonumber \]

por lo tanto, el valor máximo es$a\text{.}$

Hay algunos modelos más que van a aparecer de vez en cuando y que vale la pena mencionar.

Funciones Inversamente Proporcionales.

Si vemos la frase de que dos cantidades son inversamente proporcionales, significa que$f(x)$ es un tiempo constante$1/x\text{.}$ Podríamos esperar usar tal modelo cuando se gastará una cantidad fija de dinero para adquirir la totalidad de un producto dado. Así podemos verlo utilizado para describir el precio como una función de la oferta.

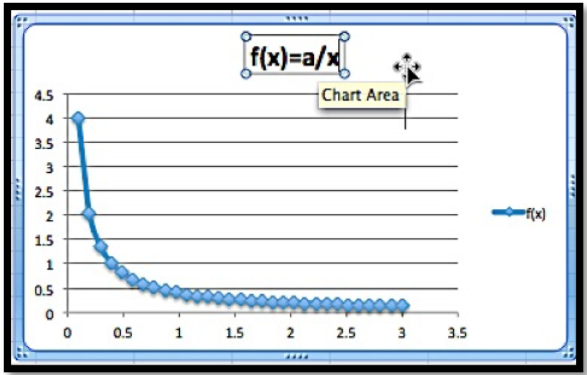
$clipboard_eed5879b413a98fe8ed914c246936aa18.png$

Funciones logarítmicas.

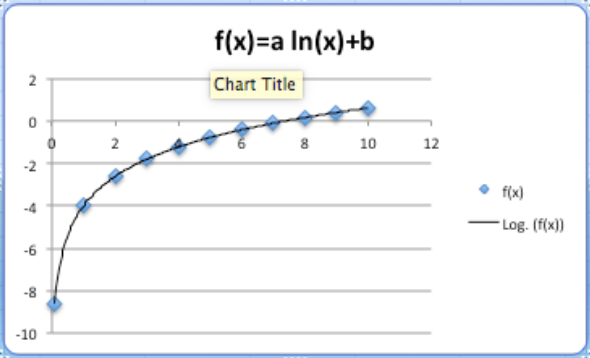
El modelo logarítmico mira las ecuaciones de la forma$f(x)=a*\ln (x)+b$ o$f(x)=a*\ln (Bx)\text{.}$ Este modelo se presenta de dos maneras. Se puede obtener como la acumulación de una cantidad que es inversamente proporcional a nuestra variable. También se manifiesta como la inversa del modelo exponencial. (Si$y$ se describe como una función exponencial de$x\text{,}$ entonces$x$ es una función logarítmica de$y\text{.}$)

$clipboard_ebc145b86ece1d3ea22ca3b8c9ce0ee8c.png$

clase=”

Ejercicios Ejercicios Funciones en el Entorno Empresarial

Para cada modelo, se listan algunas características de la gráfica. Describir cómo cambiar cada característica cambiando los parámetros del modelo. (e.g., Con el modelo lineal,$f(x)=a x+b\text{,}$ los parámetros son$a$ y$b\text{.}$ El lugar donde la línea intercepta el$x$ eje es$–b/a\text{,}$ para que cualquier$x$ -intercepción se pueda producir con$a=-1$ e$b$ igual al valor deseado.)

Ejercicio 1:

Para un modelo lineal,$f(x)=a x+b\text{,}$ ¿cómo obtengo una gráfica con

$y$¿Una intercepción positiva?
¿Una pendiente negativa?

Contestar

Cómo obtener una$y$ intercepción positiva. - La$y$ -intercepción está determinada por$b\text{,}$ lo que simplemente dejamos$b\gt 0\text{.}$
Cómo obtener una pendiente negativa. - La pendiente está determinada por$a$ en la fórmula anterior, así que dejamos$a\lt 0$

Ejercicio 2:

Supongamos que estamos trabajando con un modelo cuadrático,$f(x)=a x^2+b x+c$

¿Cómo obtenemos una gráfica, que apunta hacia abajo? (es decir, una gráfica que tiene un máximo)?
¿Cómo sabremos si la gráfica de la función intercepta el$x$ eje -en dos valores positivos?

Ejercicio 3:

Para un modelo cuadrático,$f(x)=a x^2+b x+c\text{,}$ ¿Cómo obtengo una gráfica donde tiene el vértice$x=5\text{?}$

Contestar

Los cuadráticos son parábolas y los ceros (si existen) están en$x= \frac{-b\pm \sqrt{b^2-4ac}}{2a}\text{.}$

El vértice siempre se encuentra en$x= \frac{-b}{2a}\text{.}$ Así que si el vértice va a estar en$x = 5$ necesitamos asegurarnos$\frac{-b}{2a}=5\text{.}$ Hay muchas formas de hacer esto (hay infinitamente muchas parábolas diferentes con su vértice ubicado en x = 5). Una posible solución sería dejar$b = -10$ y$a = 1\text{.}$

Ejercicio 4:

Para un modelo polinomial,$f(x)=a_n x^n+\cdots+a_1 x+a_0\text{,}$ ¿cómo obtengo una gráfica que sube en ambos extremos?

Ejemplo 5:

Para un modelo exponencial,$f(x)=P*\exp(r x)\text{,}$ ¿cómo obtengo una gráfica con$f(0)=100\text{,}$ que va a cero a medida que x se agranda?

Solución

$f(0)=P*\exp(0)= P\text{,}$así que si$f(0)=100$ sabemos que$P=100\text{.}$
Si$f$ va a 0 como$x$ se vuelve grande debe ser una función de decaimiento exponencial lo que significa que el coeficiente$r$ debe ser negativo.

Ejercicio 6:

Para un modelo exponencial,$f(x)=P*\exp(-r x)+b\text{,}$ ¿cómo consigo una gráfica donde$f(x)$ va a 10 como$x$ se hace grande,$f(0)=1\text{,}$ y$f(10)$ es al menos$9\text{?}$

Ejercicio 7:

Para un modelo de crecimiento logístico,$f(x)=\frac{M}{1+a \exp(-r*t)}\text{,}$ ¿cómo obtengo una gráfica donde$f(x)$ va a$10$ como$x$ se hace grande,$f(0)=1\text{,}$ y$f(10)$ es al menos$9\text{?}$

Contestar

Aquí tenemos varias condiciones que hay que cumplir. Los usamos para encontrar nuestros parámetros uno a la vez.

$f(x)$va a$10$ como$x$ se hace grande. Si$-r\gt 0\text{,}$ entonces$a\exp(-r*x)$ se pone muy grande como$x$ se hace grande que enviaría$f$ abajo a$0\text{,}$ pero$f$ va a$10.$ Así que sabemos que$-r\lt 0\text{.}$

Cuando$-r\lt 0\text{,}$$\exp(-r*x)$ va a$0$ para grande$x\text{.}$ Así que toda la ecuación debe ir a$M\text{.}$ Por lo tanto$M=10$

$f(0)=1\text{.}$Cuando$x = 0$ lleguemos$f(x)=M/(1+a \exp(0) )=M/(1+a)=10/(1+a)=1\text{,}$ Por lo tanto$a = 9$

$f(10)$es al menos$9\text{.}$ Con$M = 10$ y$a = 9$ tenemos eso$f(10)=10/(1+9 \exp(-r*10) )\gt 9$ Esto implica eso$1+9 \exp(-r*10)\lt 10/9$ y por lo tanto$\exp(-r*10)\lt 1/81$ Esto significa que$r\gt -1/10 \ln(1/81)= 0.44$

Ejercicio 8:

Para un modelo sinusoidal,$f(x)=M+A \sin(2\pi(x+\text{shift})/\text{period})\text{,}$ basado en el cambio estacional a lo largo del año, si$x$ se mide en meses, ¿qué valor debe tener el periodo?

Ejercicio 9:

Para un modelo normal,$f(x)=a \exp\left(-\left(\frac{x-m}{s}\right)^2\right)\text{,}$ ¿cómo puedo producir una gráfica con un punto alto en$(7, 20)\text{,}$ y el valor de$f(4)$ entre 1 y 2? (Debe usar prueba y error en este problema).

Contestar

El punto alto de la gráfica se produce cuando$\frac{x-m}{s}=0\text{.}$ Esto sucede en$x = 7\text{,}$ así que esto significa que$m = 7$ también.

Una vez que sabemos que$m = 7\text{,}$ entonces$f(7)=a \exp\left(-\left(\frac{7-7}{s}\right)^2 \right)=a \exp(0)=a$ Pero$f(7)=20\text{,}$ así$a = 20\text{.}$ Esto significa que$f(x)=20 \exp\left(-\left(\frac{x-7}{s}\right)^2\right)\text{.}$

Si el valor de$f(4)$ está entre$1$ y$2\text{,}$$f(4)=20 \exp\left(-\left(\frac{4-7}{s}\right)^2\right)$ está entre$1$ y$2\text{.}$ Podemos resolver para$s$

\[ 1\lt 20 \exp\left(-\left(\frac{4-7}{s}\right)^2\right)\lt 2 \nonumber \]

\[ 1/20\lt \exp\left(-\left(\frac{4-7}{s}\right)^2\right)\lt 1/10 \nonumber \]

\[ \ln (1/20)\lt \left(-\left(\frac{4-7}{s}\right)^2\right)\lt \ln (1/10) \nonumber \]

\[ \ln (1/20)\lt \frac{-9}{s^2}\lt \ln (1/10) \nonumber \]

y por lo tanto

\[ 2.3026\lt \frac{9}{s^2} \lt 2.996 \nonumber \]

Así$s^2\gt \frac{9}{2.996}$ y por$s^2\lt\frac{9}{2.3026} \text{.}$ lo tanto$1.734\lt s\lt 1.977\text{.}$

Ejercicio 10:

Para un modelo normal,$f(x)=a \exp\left(-\left(\frac{x-m}{s}\right)^2\right)\text{,}$ ¿cómo puedo producir una gráfica con un punto alto en$(7, 20)\text{,}$ y el valor de$f(1)$ entre 1 y 2? (Debe usar prueba y error en este problema).

Ejercicio 11:

Para el modelo de potencia,$f(x)=a x^b\text{,}$ ¿cómo puedo producir una gráfica con$f(1)=5$ y$f(3)=1\text{?}$

Contestar

$f(1)=5$significa que$a 1^b=a=5\text{.}$

$f(3)=1$significa que$a x^b=5*3^b=1$ por lo tanto$3^b=0.2$ y por lo tanto$\ln(3^b )=\ln(0.2)\text{.}$

Entonces lo$b \ln(3)=\ln(0.2)$ que implica que$b=\ln(0.2)/\ln(3) \approx -1.465\text{.}$

Ejercicio 12:

Para el modelo inversamente proporcional,$f(x)=a/x\text{,}$ ¿cómo puedo producir una gráfica con$f(1) \lt 0$ y$f(3)=-5?$

Ejercicio 13:

Para el modelo logarítmico,$f(x)=a \ln(x)$ ¿cómo puedo producir una gráfica con$f(e)=3\text{?}$

Contestar: $f(e)=a \ln(e)=a (1)= a\text{,}$de ahí$a = 3$

Para cada situación, explica qué modelo usarías para cada situación (lineal, cuadrática, etc.). Asegúrese de mencionar explícitamente lo que está usando como la variable libre (el equivalente de x), lo que está usando como la variable dependiente (el equivalente de y), y por qué ese modelo tiene sentido en la situación dada.

Ejercicio 14:

El costo de producir una cantidad de un producto es la suma de los costos fijos, como renta de almacén, y los costos variables, como mano de obra y materiales, que podemos suponer que son los mismos para cada unidad producida.

Ejercicio 15:

Al mirar los ingresos, podemos suponer que las ventas serán función lineal del precio del objeto.

Contestar

Usando un modelo lineal obtenemos$\Sales=m *\price+b\text{.}$

Precio es la variable libre (la entrada) y ventas es la variable dependiente (la salida)

Ejercicio 16:

El monto que espero poder retirar de una cuenta en una fecha futura, suponiendo que los intereses se compongan continuamente y sean fijos.

Ejercicio 17:

La cantidad de tiempo que tarda una inversión en duplicarse asumiendo una tasa de interés fija.

Contestar

El valor futuro viene dado por$FV=PV*(1+r)^t$

Aquí el valor Futuro ($FV$) será la entrada (será$2*PV$) y la salida será el tiempo$t\text{.}$

Ejercicio 18:

La cantidad de electricidad necesaria para los aires acondicionados en un Washington, D.C. en diversas épocas del año.

Ejercicio 19:

La cantidad de metal necesaria para construir un tanque de combustible en función de la cantidad de combustible a almacenar.

Contestar

El volumen es tridimensional y el metal estaría relacionado con el área de superficie —que es bidimensional— por lo que la fórmula sería algo así como:

\[ \text{Amount of metal}=K*(V)^{3/2}\text{.} \nonumber \]

$V$es la entrada, la$K$ es alguna constante y$\text{Amount of Metal}$ es la salida.

Ejercicio 20:

La longitud total de los auges necesarios para contener un derrame de petróleo en función del tamaño del derrame.

Ejercicio 21:

Las ventas mensuales de un nuevo dispositivo electrónico caliente en un país.

Contestar

Es probable que las ventas aumenten mucho inicialmente, pero luego se nivelarán. Entonces una ecuación logística puede ser un modelo razonable.

\[ f(x)= M/(1+a e^{-rx} )\text{.} \nonumber \]

Ejercicio 22:

La distribución de ventas de pares de pantalones por longitud de pierna.