1.6: Encontrar soluciones numéricas con Goal Seek

Última actualización
Guardar como PDF

Page ID: 115972

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En secciones anteriores analizamos decidir sobre un modelo para usar para datos numéricos, y encontrar la mejor curva de ajuste de ese modelo para nuestros datos. Una vez que hemos completado esas fases del proceso, hemos reducido nuestros datos a una ecuación. En ese punto queremos usar la ecuación para responder alguna pregunta. A veces esa pregunta se reducirá a resolver una ecuación, como cuando tenemos una ecuación para el beneficio en función de las ventas y queremos saber cuándo el negocio se parará. En otras ocasiones queremos saber qué entrada da una salida deseada. (por ejemplo, ¿Cuánto necesito vender para ganar $100,000 en comisión?)

Obviamente podemos utilizar todas las técnicas algebraicas que desarrollamos en cursos anteriores para resolver simbólicamente nuestro problema. Sin embargo, Excel nos da dos herramientas para usar para resolver problemas numéricamente, Goal Seek y Solver. En esta sección exploraremos Goal Seek, la más simple de estas herramientas.

Utilizaremos la búsqueda de objetivos si sabemos cuál es la salida deseada de una ecuación, y nos gustaría saber cuándo se logra esa salida.
Necesitamos tener una ecuación con la que trabajar y solo podemos resolver para un tipo de entrada (variable).
Goal Seek se encuentra bajo el menú de análisis Qué pasaría si.

Ejemplo 1.6.1: Un Ejemplo Lineal.

Figura Presentación en$1.6.2.$ video de este ejemplo

Al igual que con todas las nuevas técnicas en una clase de matemáticas, comenzamos con un ejemplo muy sencillo que puedes resolver fácilmente por métodos que aprendiste en cursos anteriores. Supongamos que tenemos la función$f(x) = 3 x + 5\text{,}$ y quiero encontrar el valor de$x$ donde$f(x) = 40\text{.}$ empiezo configurando una hoja de trabajo con$x$ y$f(x)$ como columnas. También necesito comenzar con un valor adivinado, que puede ser cualquier número. Empezaré por adivinar un valor de 5. (Voy a introducir ese valor dos veces para que podamos ver antes y después.)

Después voy a la pestaña de datos y debajo del menú de análisis Qué pasaría si elijo Búsqueda de objetivos. En el cuadro de diálogo Búsqueda de objetivos, quiero cambiar B3,$f(x)\text{,}$ a 40 cambiando A3, o$x\text{.}$ después selecciono OK.

Excel encuentra el valor y pregunta si está bien reemplazar la suposición inicial con ese valor. En este caso, Excel encontró el valor de$11.66666667$ o$35/3\text{,}$ que también podríamos haber encontrado por álgebra simple.

Ejemplo 1.6.3: Un ejemplo cuadrático y preocupación por la precisión.

Pasamos a un ejemplo cuadrático. Dejamos$f(x)=x^2$ y queremos encontrar$f(x)=2\text{.}$ La configuración es similar, con un cambio apropiado en la ecuación. Sin embargo cuando uso Goal Seek, no obtengo la respuesta correcta.

En lugar de encontrar un valor con$x^2 = 2\text{,}$ encontré un valor con$x^2 = 1.99999495\text{.}$

Observamos que Excel no está resolviendo el problema algebraicamente, sino que está encontrando una aproximación numérica dentro de una tolerancia preestablecida.
En realidad es encontrar una x tal que f (x) esté dentro de 0.001 de 2.

Para la mayor parte de nuestro trabajo, eso está lo suficientemente cerca. A veces, sin embargo, tal vez queramos más precisión. (Nuestras unidades pueden ser de millones de dólares.) En ese caso, podemos mejorar la precisión con un trabajo alrededor. Agregamos otra celda con una fórmula cuyo valor es un número grande, digamos$10^6\text{,}$ veces el error. Luego usamos Goal Seek para hacer que ese valor se acerque a cero. Reducimos efectivamente nuestra tolerancia a errores por un factor de nuestro gran número. Aplicando esto a nuestro ejemplo da:

Esto ha calculado el valor de la raíz cuadrada de 2 a 10 dígitos.

Ejemplo 1.6.4: Ejemplos más realistas: Encontrar la intersección de dos curvas, o encontrar equivalentemente dónde dos funciones son iguales entre sí..

Figura Presentación en$1.6.5.$ video de este ejemplo

En economía, están los conceptos de precios de oferta y demanda, los precios que producirán una oferta o demanda especificada. (Analizaremos este problema con más profundidad en el próximo capítulo.) Supongamos que se nos dice que la fórmula para los precios de oferta y demanda de un producto son:

\[ Supply\ Price (q) = ln(50 + 1000 q) + q \nonumber \]

\[ Demand\ Price (q) = 1000*exp(-0.02*q)\text{.} \nonumber \]

Queremos encontrar la cantidad donde los precios de oferta y demanda son iguales. Primero hacemos una gráfica rápida para entender lo que está pasando.

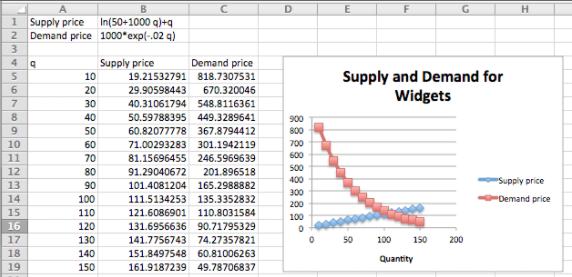
$clipboard_e0df65474cf633b91d4e96e8ce848e54d.png$

Podemos ver que las curvas se cruzan cuando q está en algún lugar entre 100 y 110. Para hacer de esto un problema de búsqueda de objetivos agregamos una columna extra para la diferencia entre oferta y demanda, y buscamos donde eso es cero.

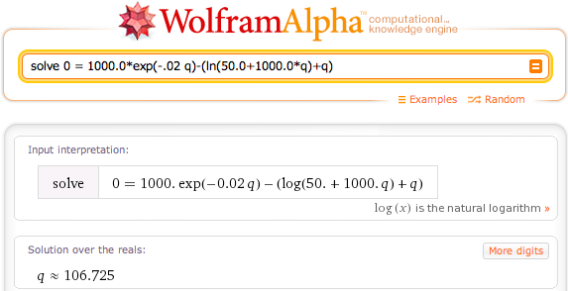
Vemos que el equilibrio ocurre cuando q es 106.725. Podríamos haber encontrado esto algebraicamente resolviendo la ecuación

\[ 0 = 1000*exp(-0.02*q) – (ln(50 + 1000*q) + q)\text{,} \nonumber \]

pero ese no es un problema fácil.

Nuestro último ejemplo para Goal Seek analiza los cálculos financieros.

Ejemplo 1.6.6: Uso de la Búsqueda de Objetivos para Cálculos Financieros.

Figura Presentación en$1.6.7.$ video de este ejemplo

Supongamos que has decidido abrir una cuenta de retiro cuando salgas de la universidad. Tú decides que empezarás aportando $2,000 al inicio de cada año, con ese monto aumentando en $100 cada año, asumiendo una tasa de interés anual del 5%. Las fórmulas relevantes son:

\ begin {align*}\ text {Saldo Final}\ amp =\ text {Saldo Inicial + Depósitos + Intereses Ganados}\\\ text {Intereses Ganados}\ amp =\ text {(Comienzo\ Saldo + Depósitos) * Interés\ Tasa}\\\ texto {Saldo Inicial}\ amp =\ texto {anterior\ año\ final\ saldo}\ texto {.} \ end {alinear*}

Se vuelve fácil configurar una hoja de cálculo para calcular el saldo al final de 40 años.

(Veremos este ejemplo con mayor detalle en un capítulo posterior. Por ahora, tenga en cuenta que este ejemplo está en el cuaderno de Excel para esta sección.) Podemos ver que tenemos un poco más de $420,000 después de 40 años.

Con Goal Seek es fácil plantearse la pregunta de cómo necesitamos cambiar el problema para tener un saldo de 500.000 dólares después de 40 años, ya sea cambiando el depósito inicial, o la tasa a la que van aumentando los depósitos, o el rendimiento esperado. Vemos que necesitamos un rendimiento de 5.74% para tener 500 mil dólares listos para el retiro.

Vale la pena señalar que en este caso nuestro saldo final es el resultado de un cálculo de 120 pasos con nuestra variable de entrada. Goal Seek encuentra una solución sin que tengamos que reducir ese cálculo de 120 pasos a una sola fórmula larga.

Ejemplo 1.6.8: Mirar bajo el capó y comprender las limitaciones de Goal Seek.

Al igual que con cualquier herramienta que utilicemos, es aconsejable tener alguna comprensión del método utilizado por Goal Seek. Eso nos ayudará a entender cuándo nos está dando una respuesta diferente a la que esperábamos, o incluso nos da una respuesta que está equivocada.

Figura Presentación en$1.6.9.$ video de este ejemplo

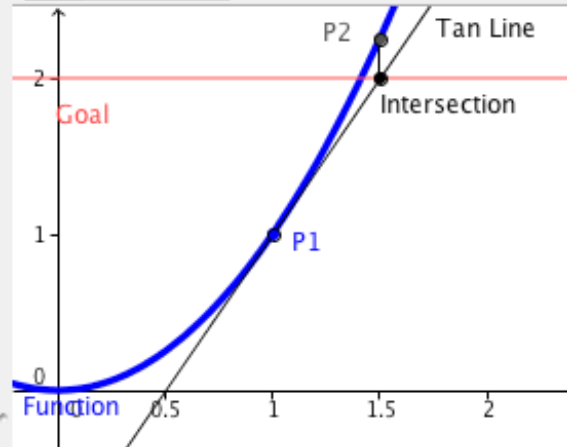
Goal Seek utiliza el Método de Newton, una técnica basada en Cálculo, para encontrar soluciones. El corazón del método se basa en el hecho de que, al menos para la mayoría de las funciones lo suficientemente agradables como para aparecer en un curso como este, cuando acercas lo suficiente en una gráfica obtendrás algo que parece una línea recta. La línea que encontramos de esa manera se llama la línea tangente. (Encontrar la pendiente de la línea tangente, o la tasa instantánea de cambio, es uno de los principales objetivos del cálculo, y se le da el nombre de encontrar la derivada.) Si comenzamos con una solución adivinada, podemos producir una línea tangente, encontrar el punto donde la línea tangente alcanza el valor deseado y tomar la coordenada x del punto como nuestra siguiente conjetura. Repetir este proceso suele converger en una solución.

$clipboard_e2c149900907488c97523d34d31f43bda.png$

Si usamos la hoja de cálculo para ilustrar el método de Newton para nuestro ejemplo, al encontrar la solución para$x^2 = 2$ comenzar con una suposición de$x = 1\text{,}$ vemos que converge en 5 iteraciones. (En este punto, simplemente estamos ilustrando cómo funciona Goal Seek. Aún no se espera que puedas replicar el proceso. Aprenderás a encontrar la pendiente de la tangente en capítulos posteriores.)

Como se mencionó anteriormente, la razón para mirar bajo el capó de Goal Seek es entender cuándo nos da una respuesta inesperada. Una descripción simplificada del método utilizado es que se dirige a donde espera encontrar una solución y repite el proceso hasta que esté dentro de 0.001 de la respuesta deseada. Existen varias maneras fáciles de que este método cause problemas.

Figura$1.6.10.$ Más video para este ejemplo

La primera dificultad es que Goal Seek puede no darte la respuesta que buscas si hay múltiples respuestas. La función$f(x) = x^3 – x$ tiene tres raíces,$x = -1, 0, 1\text{.}$ Si le damos a Goal Seek un punto de partida de la$x=.55\text{,}$ misma dará la solución de$x=0\text{.}$

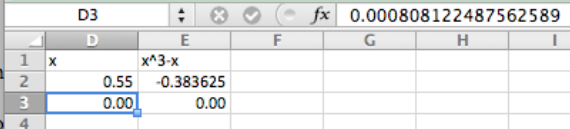
$clipboard_eaa3bc37e00ea397bfa29a322519d94c8.png$

Como regla general, Goal Seek llegará a la respuesta correcta si no hay grandes curvas entre la conjetura y la respuesta. Otra dificultad surge si le preguntas a Goal Seek una pregunta para la que no hay respuesta. El caso fácil es cuando no hay respuesta y ni siquiera nos acercamos. Podríamos pedirle que encuentre una x con$x^2+1=0\text{.}$ Ya que sabemos que todos los cuadrados son no negativos, esto no tiene respuesta. Goal Seek nos dirá eso, pero hará algunas conjeturas bastante salvajes.

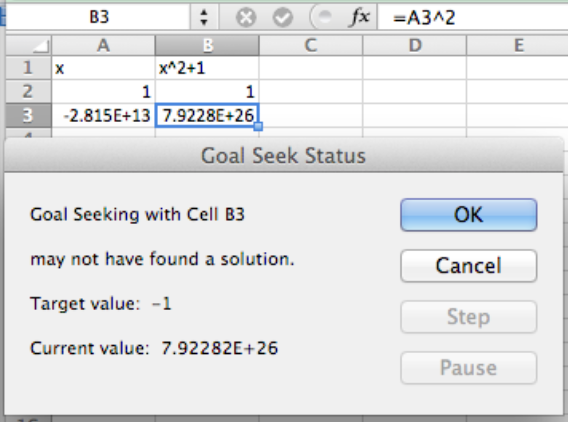
$clipboard_e08ee686d09357682386764e7545a7b36.png$

En este caso Goal Seek se ejecutará por un número fijo de iteraciones y nos dirá que “puede que no haya encontrado una solución”. En ese caso nos dirá dónde terminó y nos dará la opción de aceptar ese punto, o cancelar y volver a donde empezamos. Si no hay solución y uno de nuestros puntos intermedios estuvo cerca de un punto con una línea tangente plana, podemos terminar en cualquier lugar.

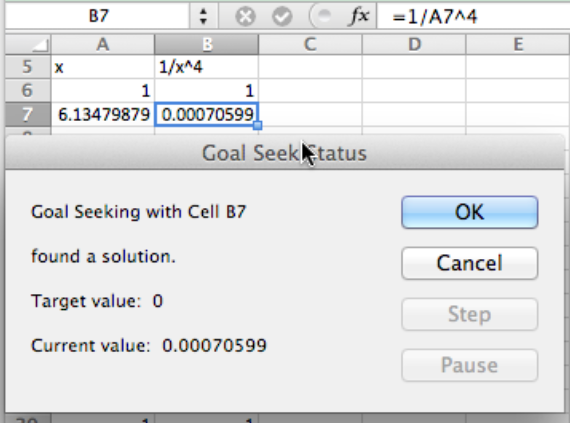
El caso más desafiante surge cuando no hay respuesta, pero nos acercamos. Podemos pedirle a Goal Seek que encuentre una x con$1/x^4 = 0\text{.}$ Claramente este problema no tiene respuesta. No obstante, si empezamos con una suposición de$x = 1\text{,}$ obtenemos una respuesta de$x = 6.14798\text{.}$ Eso es porque$1/6.14798^4$ está dentro de nuestra tolerancia de 0. En ambos casos vemos que cuando usamos Goal Seek también debemos mirar la gráfica de la función en cuestión para asegurarnos de que estamos haciendo una pregunta razonable.

$clipboard_e670535e4505f86da2c72603cfbc9968d.png$

De vez en cuando aparece una variante de estos problemas. Si comenzamos con un problema cuidadosamente amañado podemos establecer el algoritmo de Búsqueda de objetivos en un bucle. Si empezamos con la función$f(x) = x^3 – 50*x$ con una suposición inicial de$x=1\text{,}$ y preguntamos a Goal Seek para encontrar cuándo$f(x) = 500\text{,}$ Goal Seek no encontrará una respuesta. En este caso podríamos mirar una gráfica y hacer una suposición inicial de 6, para luego obtener una respuesta correcta. Una vez más, con un método numérico, vale la pena probar algunos casos y asegurarnos de que nuestra suposición esté cerca de una respuesta razonable. Si$f(x)$ es una función continua, esto significa encontrar un valor de$x$ donde$f(x)$ es demasiado bajo y otro valor donde$f(x)$ es demasiado alto.

Si bien Excel es una herramienta poderosa, siempre debemos preguntar si hay una manera más fácil de hacer un problema. La mayoría de los ejemplos que vimos en esta sección se reducen a encontrar una solución a$f(x)=0$ donde$f(x)$ es una ecuación simple. Podemos resolver este tipo de problemas más rápidamente con Wolfram Alpha.

$clipboard_eebac8b13775c6044880e7e33b3fec685.png$

Como se señaló anteriormente, Goal Seek es muy útil para problemas con muchos pasos donde tendríamos dificultades para reducir el problema a una sola ecuación.

Encontrar soluciones numéricas con Goal Seek

clase=”

Use Objetivo Buscar para encontrar dónde la ecuación dada tiene el valor deseado.

Ejercicio 1:

Vamos a$f(x) = -2 x^2 + 20 x + 7\text{.}$ encontrar un$x$ modo que$f(x) = 50\text{.}$

Contestar: Wolfram detecta dos soluciones.

Ejercicio 2:

Vamos a$f(x) = -x^2 + 4 x + 5\text{.}$ encontrar un$x$ modo que$f(x) = -5\text{.}$

Ejercicio 3:

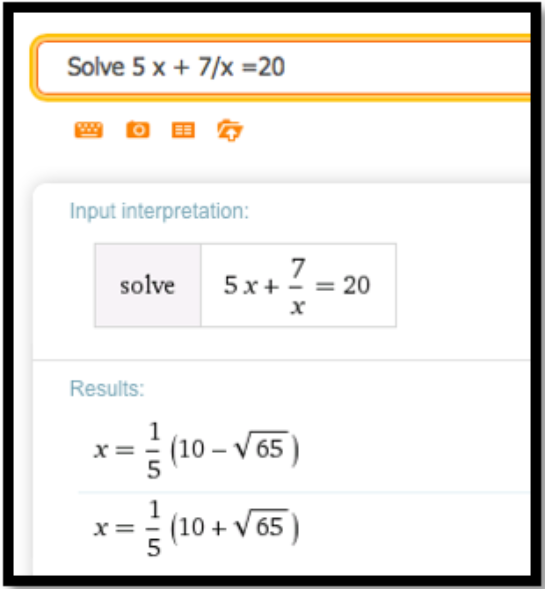
Vamos a$f(x) = 5 x + 7/x\text{.}$ encontrar un$x$ modo que$f(x) = 20\text{.}$

Contestar: $clipboard_edda4a8817b930046d3ea95191b37aff5.png$

Ejercicio 4:

Vamos a$f(x) = 10 \exp(x/10)\text{.}$ encontrar un$x$ modo que$f(x) = 1000\text{.}$

Ejercicio 5:

Vamos a$f(x) = \ln(x+5) + 7\text{.}$ encontrar un$x$ modo que$f(x) = 5\text{.}$

Contestar

Tenga en cuenta que al lado de la solución hay un botón para “Formulario aproximado”

Podemos usar eso para obtener una aproximación decimal:

$clipboard_e460702a4054b10802b06b0413f1547fc.png$

Tenga en cuenta que podemos obtener más dígitos si queremos o volver a la respuesta exacta

Ejercicio 6:

Vamos a$f(x) = 1000*(1/2)^{(x/7)}\text{.}$ encontrar un$x$ modo que$f(x) = 50\text{.}$

Utilice la búsqueda de objetivos para encontrar el número indicado de puntos donde se cruzan las curvas

Ejercicio 7:

Encuentra un punto de intersección de$f(x) = 5 x + 7$ y$g(x) = 40 – 2 x\text{.}$

Contestar: Encontrar el punto de intersección significa que estamos estableciendo las dos ecuaciones iguales entre sí. Wolfram incluirá una gráfica de la solución así como la respuesta numérica.

Wolfram nos dice que$x=\frac{33}{7}\text{.}$ podemos enchufar eso en una de las ecuaciones y obtener

\[ y=40-\frac{66}{7}=\frac{280}{7}-\frac{66}{7}=\frac{214}{7}\text{.} \nonumber \]

Entonces el punto de intersección es$(x,y)=(\frac{33}{7} ,\frac{214}{7})\text{.}$

Ejercicio 8:

Encuentra un punto de intersección de$f(x) = 5 x$ y$g(x) = 9 x / 7\text{.}$

Ejercicio 9:

Encuentra un punto de intersección de$f(t) = \exp(-0.05 t)*(3 t + 5)$ y$g(t) = t/10\text{.}$

Contestar

Wolfram encuentra dos intersecciones: una en$t\approx-1.71925$ y la otra en$t\approx68.5047$

Usando la función$g(t)=t/10$ obtenemos los dos puntos de intersección en$(-1.71925,-.171925)$ y$(68.5047,6.85047)\text{.}$

Ejercicio 10:

Encuentra un punto de intersección de$f(t) = 20 \ln(100 t + 854)$ y$g(t) = 0.02 t\text{.}$

Ejercicio 11:

Encuentra ambos puntos de intersección de$f(x) = 7 + 10 x – x^2$ y$g(x) = 0\text{.}$

Contestar: Las$y$ coordenadas -deben ser 0. Si utilizamos la forma aproximada de la solución obtenemos$(-0.65685,0)$ y$(10.657,0)\text{.}$

Ejercicio 12:

Encuentra ambos puntos de intersección de$f(x) = 15 x + 200/x$ y$g(x) = 20 + 25 x\text{.}$

Ejercicio 13:

Tenemos razones para creer que la función de ganancia para la fabricación de widgets está modelada por una ecuación cuadrática. Tenemos los siguientes datos para ventas y ganancias.

Ventas	100	250	350	500	600
Beneficio	$8,462	$18,378	22,455	24,400	23,747

Encuentre la mejor curva de ajuste para los datos.
Encuentra los dos puntos de equilibrio, o cantidad de ventas que producen una ganancia de $0.

Contestar

Usando Excel encontramos el polinomio de mejor ajuste de orden 2:

$y = -0.1006x2 + 100.66x - 555.65$
Usando Wolfram luego encontramos donde la ganancia es 0. Usar la forma aproximada de la solución es preferible en este caso porque queremos saber en qué Ventas tenemos 0 ganancia (los puntos de equilibrio).

Los puntos de equilibrio están en ventas de 5.55 y 995.05.

Ejercicio 14:

Un determinado banco dará un bono de $75 en una nueva cuenta con un depósito de $1000, y luego paga 5% de intereses compuestos continuamente. Una segunda oportunidad de inversión pagará $100 anuales.

¿Qué oportunidad paga más en el primer año?
¿Para qué periodo de tiempo ofrecen las dos oportunidades el mismo retorno?
¿Cuál es el pago de las dos oportunidades para una inversión de 30 años?
¿Cuál es el segundo periodo de tiempo en que las dos oportunidades ofrecen el mismo retorno?

Ejercicio 15:

Let$f(x) = (10 x-1) *\exp(-x) + 2\text{.}$

Encuentra una solución con Goal Seek comenzando por x=1.
¿Qué sucede cuando Goal Seek intenta encontrar una solución a partir de$x=2\text{?}$
Explique por qué, a partir de la gráfica de$f(x)\text{,}$ debemos esperar este problema.

Contestar

La entrada en la celda B2 es = (10*A2-1) *EXP (-A2) +2

Porque$x = 1$ como punto de partida GoalSeek encuentra un cero en$x\approx-0.0839$