1.5: Usar Excel para encontrar las curvas de mejor ajuste
- Page ID
- 115960
En la Sección 1.1—1.2 analizamos modelos matemáticos y fórmulas útiles que anticipamos ver repetidamente en el entorno empresarial. Si se nos dan ecuaciones que modelan los procesos que nos interesan, entonces este enfoque funciona. Sin embargo, ¿qué pasa si no se nos dan ecuaciones? Muchas funciones importantes en los negocios a menudo se definen por los datos. Los ejemplos incluyen ventas pasadas, costos de materiales y demanda de los consumidores.
Si se nos da un conjunto de datos, podemos encontrar una curva de mejor ajuste. Un enfoque sencillo es asumir que los datos representan la salida de una fórmula agradable. En aplicaciones de la vida real a menudo veremos que el llamado ruido puede complicar la situación. (Por ejemplo, si estoy buscando ventas en un restaurante de comida rápida, nuestro modelo tendrá ruido de atascos y mal tiempo afuera). A los efectos de este curso asumiremos que los datos serán razonablemente agradables, aunque algún ruido puede ser evidente. El problema de producir una curva de mejor ajuste a los datos puede dividirse en dos partes:
- Tenemos que decidir qué tipo de curva, o qué modelo queremos utilizar.
- Queremos poder establecer los parámetros (las constantes) en el modelo para dar el mejor ajuste.
Elaborar una razón teórica por la que queremos utilizar un modelo particular en un caso dado forma el contenido de un gran número de sus cursos de negocios, tanto cursos que ya ha cursado como cursos que aún no ha cursado. A los modelos que aparecen repetidamente en los cursos teóricos se les da nombres y se utilizan sin rehacer la base teórica para el modelo. (Es por ello que introdujimos la distribución normal y la función de crecimiento logístico, ninguna de las cuales parece una ecuación simple). En este curso, estaremos contentos con simples argumentos heurísticos sobre qué modelo elegir.
La segunda mitad del problema es decidir cómo elegir los parámetros para dar la curva que hace el mejor trabajo de ajustar los datos. Un momento de reflexión muestra que decidir sobre la correcta definición de “mejor ajuste” es una tarea no trivial más allá del alcance de este curso. Por el momento aceptaremos la definición estándar:
La curva de mejor ajuste minimiza la suma de los cuadrados de las diferencias entre los valores medidos y predichos.
Volveremos a esa definición más adelante en el curso, cuando sepamos más cálculo, pero por ahora simplemente notamos que es la definición estándar, y es utilizada por Excel. En su lugar, nos enfocaremos en usar Excel para producir una curva de mejor ajuste del modelo apropiado. Excel tiene una característica preprogramada que encontrará la ecuación que mejor se ajuste para un conjunto de datos para un número selecto de funciones:
- Modelo lineal
- Modelo exponencial
- Modelo polinomial
- Modelo logarítmico
- Modelo de potencia
Mostraremos cómo encontrar una ecuación para un conjunto de datos, asumiendo que sabemos qué modelo sería el mejor para representar los datos.
\(Figure \text { } 1.5.2.\)Video presentación de este ejemplo
Para un primer ejemplo, estamos ejecutando una fábrica de widgets y tenemos los siguientes datos sobre el desempeño de los empleados:

Nos gustaría una fórmula para widgets producidos en función de las horas trabajadas. Como podemos ver dos entradas cada una, para 36, 43 y 44 horas trabajadas, no puede haber una función que golpee todos nuestros datos exactamente. Si bien esperamos una función lineal, no nos sorprende si hay ruido aleatorio, ya que un trabajador puede tomar un descanso, o estar particularmente enfocado en un día determinado. Empezamos por crear una gráfica de dispersión para mis datos.
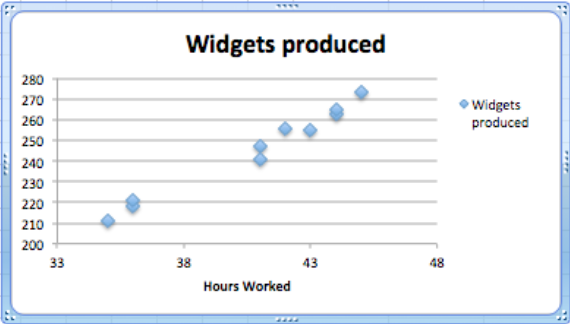
Hacemos clic derecho (control-clic en un Mac) en uno de los puntos de datos y obtenemos un menú contextual. Seleccionamos Agregar línea de tendencia.
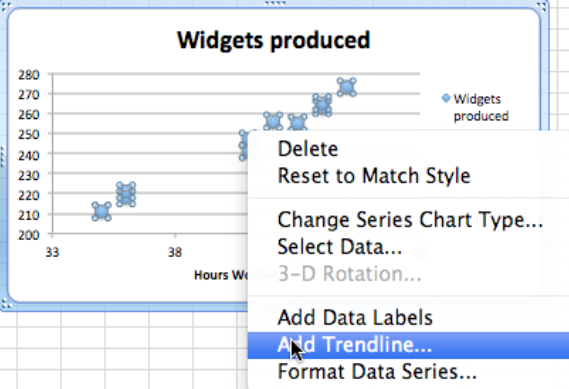
Al agregar una línea de tendencia, debemos seleccionar entre una serie de opciones. La primera opción se refiere al modelo matemático que queremos elegir. Dado que sospechamos que el número de widget producido será aproximadamente proporcional a las horas trabajadas, queremos usar un modelo lineal, por lo que hacemos esa elección. Bajo opciones, queremos mostrar la ecuación en el gráfico.
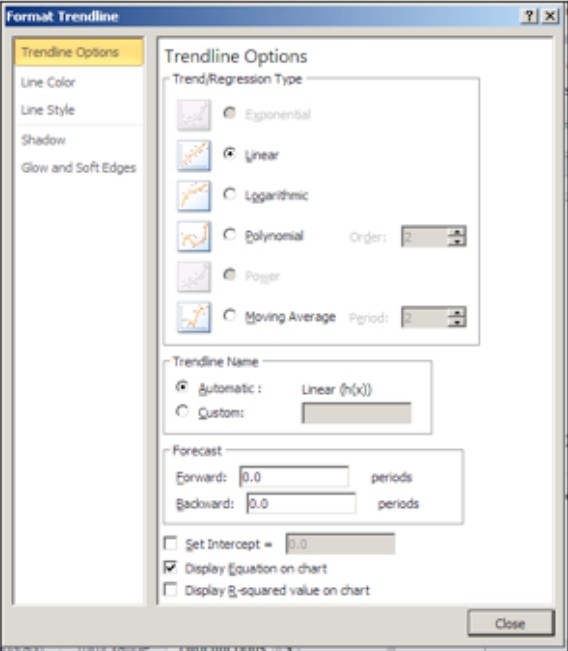
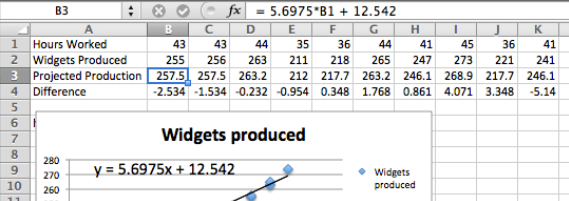
Hemos agregado una línea de tendencia lineal a la gráfica y también podemos ver la ecuación para la línea. Podríamos usar esa ecuación para planificar cuántas horas queremos que nuestros trabajadores estén en el trabajo en función del número de widgets que esperamos vender.
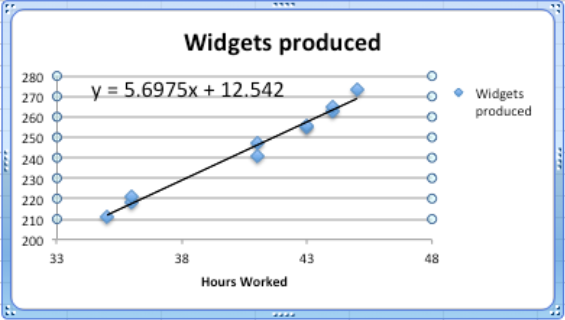
Habiendo encontrado una línea de mejor ajuste, quiero volver a copiar la ecuación en mi hoja de cálculo y poder comparar los valores de mis datos con las proyecciones de mi ecuación. Debe notar que la ecuación que Excel produce en el gráfico está escrita en notación matemática estándar, mientras que la ecuación correspondiente en la celda B3 está en notación Excel. (En la notación Excel necesitamos un símbolo para la multiplicación en lugar de simplemente poner un número y una variable juntos. En la notación Excel, también usamos una referencia de celda, B1, en lugar de una variable, x.)
\(Figure \text { } 1.5.4.\)Video presentación de este ejemplo
Al encontrar la curva que mejor se ajuste a los datos que hemos recopilado, debemos prestar atención al modelo que hemos elegido y al rango al que queremos aplicarlo. En nuestro ejemplo, el ajuste lineal se ve bastante bien. Sin embargo, debemos tener cuidado al usarlo en un dominio demasiado amplio. Según nuestro modelo, un trabajador que trabaja sin horas produce 12.52 widgets a la semana, lo que obviamente es una tontería. En la otra dirección predice que un trabajador que trabajaba 168 (= 7 × 24) horas a la semana produciría casi 970 widgets, en lugar de predecir un colapso por agotamiento.
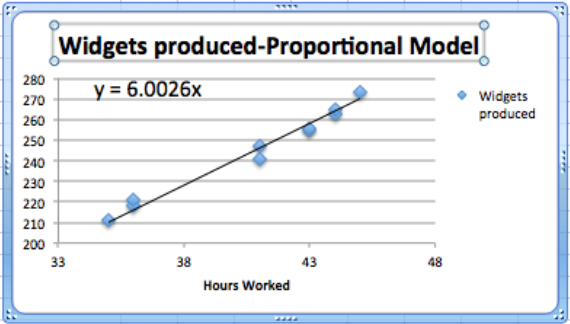
El otro tema es la elección de un modelo. Elegimos un modelo lineal. Se podría argumentar fácilmente para un modelo proporcional. (Un trabajador que trabaja sin horas no produce widgets.) Podemos cambiar al modelo proporcional estableciendo el\(y\) -intercept en 0 en las opciones para la línea de tendencia. Entonces la ecuación es
\[ (\text{Widgets Produced}) = 6.00026*(\text{Hours Worked}) \nonumber \]
en lugar de nuestra ecuación original de
\[ (\text{Widgets Produced}) = 5.6975*(\text{Hours Worked})+12.54\text{.} \nonumber \]
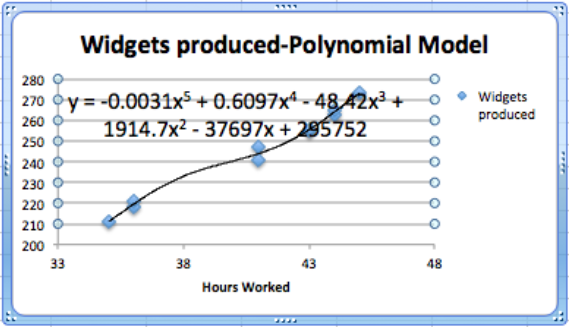
También debemos tener cuidado al tratar de conseguir un mejor ajuste mediante el uso de un modelo inapropiado. En nuestro caso, podemos obtener un mejor ajuste permitiendo que la curva sea un polinomio de 6to grado. Sin embargo, la ecuación resultante no tiene sentido. Predice que un trabajador producirá alrededor de un cuarto de millón de widgets con una semana laboral de 1 hora, y\(-1500\) widgets con una semana laboral de 55 horas.
\(Figure \text { } 1.5.6.\)Video presentación de este ejemplo
Para nuestro segundo ejemplo, veremos el índice de precios al consumidor e intentaremos ajustarlo a un modelo. Este ejemplo ilustrará varios temas que debemos tener en cuenta a la hora de construir modelos. Obtuvimos datos para el índice de precios al consumidor de http://inflationdata.com/inflation/Consumer_Price_Index/HistoricalCPI.aspx.
Los datos de 1960 a 2011 se encuentran en la hoja de trabajo Section-1-5-Examples.xlsx.
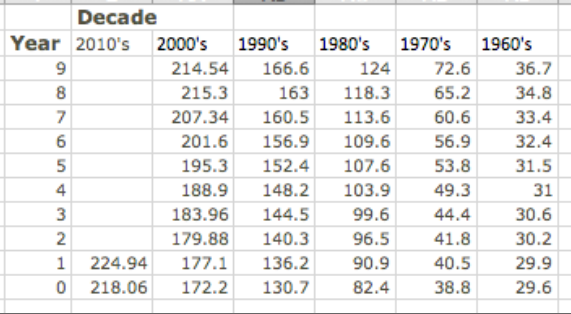
Dado que esperamos que los precios suban como porcentaje de los precios actuales, esperamos que el IPC sea modelado por una curva exponencial. Comenzamos seleccionando los datos, produciendo una gráfica de dispersión y agregando una curva de mejor ajuste usando un modelo exponencial. Siempre seleccionaremos la opción para mostrar la ecuación en el gráfico.
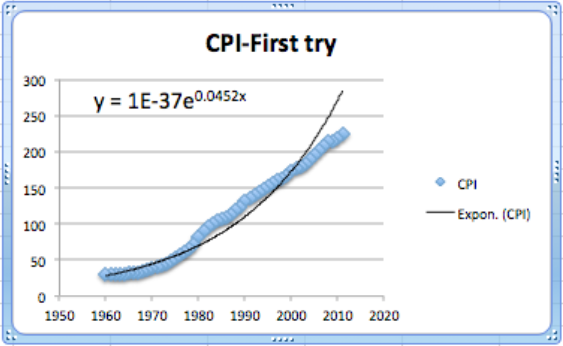
Este primer intento da una fórmula exponencial, pero es insatisfactoria por varias razones.
- Esa constante sólo muestra un dígito significativo, que no es suficiente para hacer predicciones significativas.
- El tamaño de la fuente es demasiado pequeño para leer fácilmente las ecuaciones resultantes.
- El coeficiente constante es ridículamente pequeño porque da el valor proyectado del índice en el año 0. Otra forma de pensar sobre esto es que los valores que estamos evaluando esta función exponencial a correr ¡por miles!.
- El gráfico no parece un ajuste muy bueno. La trama de los números en realidad parece que representa tres gráficas diferentes.
Trabajaremos a través de los problemas uno a la vez.
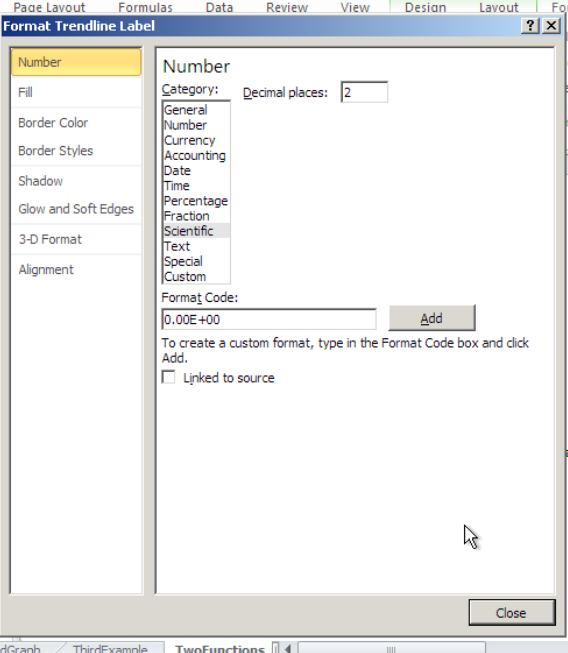
El primer problema es que la ecuación que nos ha dado Excel no tiene suficientes dígitos significativos para hacer predicciones útiles. Queremos hacer click derecho sobre la ecuación, seleccionar “Format Trendline Label”. Se nos da un cuadro de diálogo que nos permite hacer opciones de formato. Dado que el coeficiente de plomo es tan pequeño, queremos que los números estén formateados en notación científica. Elegimos 4 dígitos más allá del punto decimal en esa notación.
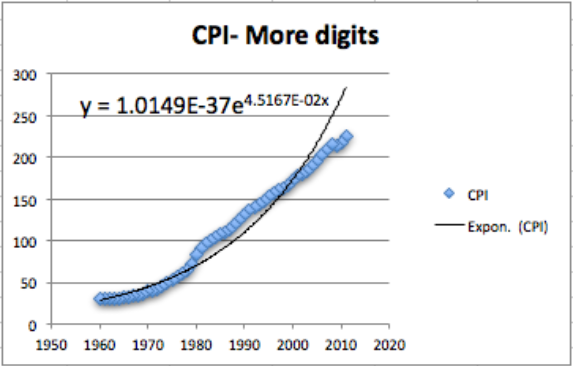
Esto nos da una mejor ecuación. Cabe señalar que nuestras imágenes en este libro utilizan la opción de fuente en el formato para usar una fuente de mayor tamaño.
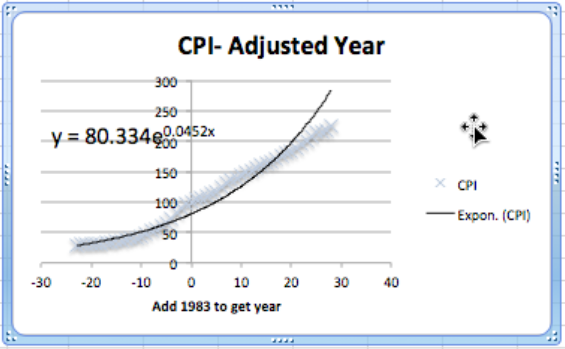
El siguiente tema a tratar es ajustar el año. Al observar los datos brutos, el IPC fue de 100 en algún momento de 1983. Así simplemente agregamos una columna extra a nuestra hoja de cálculo donde el año ajustado es el año en curso menos 1983. En nuestra gráfica, también ajustamos las etiquetas para que un lector pueda entender nuestro gráfico.
\(Figure \text { } 1.5.7.\)Continuación de la presentación en video de este ejemplo
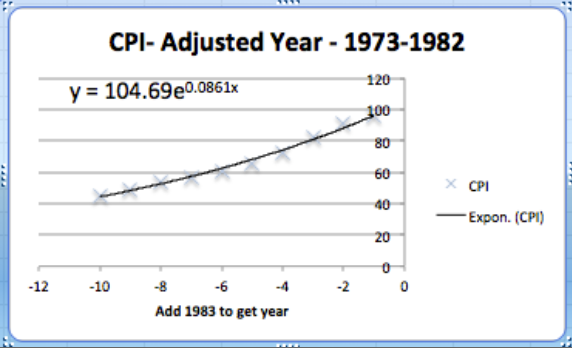
Ahora queremos mirar la pregunta más seria, la que dice que el modelo no encaja muy bien. Al observar nuestros datos, la tasa de inflación parece caer en aproximadamente 3 bloques, los años anteriores a 1973, los años de 1973-1983, y los años posteriores a 1983. Nos gustaría volver a nuestras clases de economía y encontrar un argumento que diga que esta división de años es razonable. Usando el mismo menú que nos permite agregar una línea de tendencia, podemos editar los datos de origen. Queremos restringirnos a los años posteriores a 1983. En nuestro caso, eso significa restringir a las filas 1 a 30.
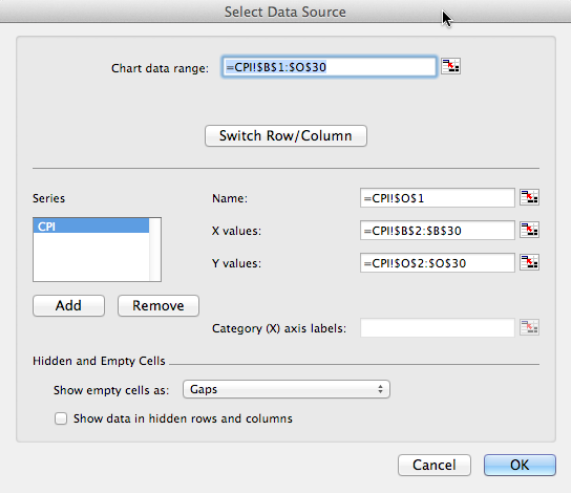
Esto divide los datos en dos partes. La primera pieza es el periodo de 1983 a 2011. Como vemos, el modelo exponencial encaja bastante bien en ese caso.
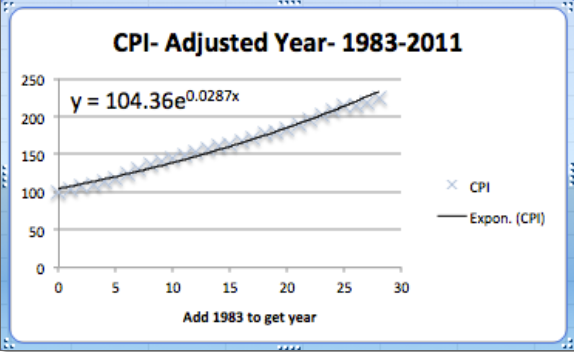
La segunda pieza es el periodo de 1973 a 1982. Una vez más, el modelo exponencial encaja bastante bien en ese periodo. Observe que el exponente es bastante diferente en los dos periodos.
La pregunta obvia que se plantea es averiguar qué sucedió en 1983 que provocó que el modelo económico cambiara. Esa pregunta está más allá del alcance de este curso.
Ejercicios: Usar Excel para encontrar las curvas que mejor se ajustan
Tenemos los siguientes datos sobre la producción de widgets:
| Mes | Ene | Feb | Mar | Abr | Mayo |
| Producción | 16,597 | 30,687 | 48,441 | 55,751 | 79,606 |
- Encuentre la función lineal que mejor se ajuste para los datos.
- Dar el valor de producción que la función predice para mayo.
- Dar el valor de producción que la función predice para julio.
- Contestar
-
- Cree una gráfica de dispersión para los datos. Después usa el menú para ir a Gráfico — Diseño de gráfico — Líneas de tendencia. Encuentra la aproximación lineal y debajo de las opciones elige mostrar la función.
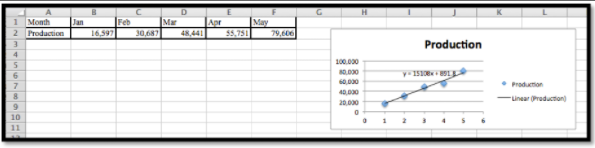

Excel cambia automáticamente los meses en valores numéricos.
La mejor función lineal para los datos es\(y = 15108x + 891.8\text{.}\)
- Crear una nueva tabla usando la función para determinar los niveles de producción previstos.

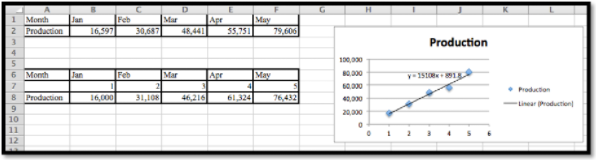
Excel necesita que x sea un número, así que necesitamos insertar una fila y proporcionar los valores numéricos apropiados: 1 para Ene, 2 para Feb, etc.
La producción pronosticada para mayo es de 76,432
- Para encontrar el nivel de producción para julio ingresamos
x = 7en la tabla y calculamos la salida.
El modelo lineal predice una producción de 106, 648 para el mes de julio.
Tenemos los siguientes datos sobre ventas de artilugios:
| Mes | Ene | Mar | Abr | julio | Ago |
| Unidades vendidas | 1.505 | 9,042 | 13,018 | 21,873 | 22,636 |
- Encuentre la función lineal que mejor se ajuste para los datos.
- Ampliar el gráfico para dar las ventas proyectadas para cada mes de enero a septiembre. (Debe agregar una fila para las ventas previstas, y también agregar una serie de columnas para los meses faltantes).
Tenemos los siguientes datos sobre ingresos de gadgets:
| Unidades vendidas | 3,000 | 5,000 | 7,000 | 9,000 | 11,000 |
| Ingresos | 16,161 | 24,783 | 34,484 | 38,014 | 33,030 |
- Encuentre la función lineal que mejor se ajuste para los datos.
- Encuentre la función cuadrática que mejor se ajuste a los datos.
- Los datos se ajustan mejor a una función cuadrática que a una función lineal. Con un modelo cuadrático no maximizamos los ingresos vendiendo tantas unidades como sea posible. Explique por qué esto es razonable en el mundo real.
- Proyectar los ingresos por vender 15,000 unidades con modelos tanto lineales como cuadráticos.
- Contestar
-
- Podemos hacer diagramas de dispersión y usar la línea de tendencia lineal para encontrar los modelos que necesitamos.

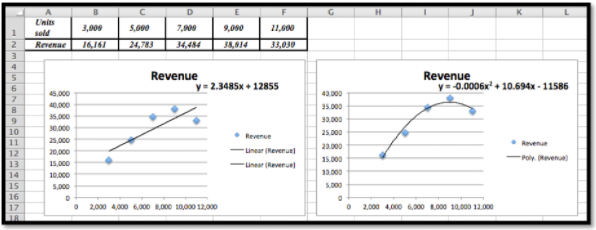
El modelo lineal es\(y = 2.3485x + 12855\)
- Podemos hacer diagramas de dispersión y usar la línea de tendencia polinomial de grado 2 para encontrar el modelo que necesitamos. (Ver la segunda imagen en la parte (a).)
El modelo cuadrático (polinomio de grado 2) es\(y = -0.0006x^2 + 10.694x – 11586\)
Las gráficas muestran que la ecuación cuadrática es el mejor modelo y sigue los datos más de cerca.
- La función de ingresos viene dada por precio * cantidad. Si ofrecemos más unidades el precio eventualmente bajará. Si el precio baja más rápido que el número de nuevos artículos vendidos, los ingresos en algún momento volverán a bajar.
- Enchufe\(x = 15000\)\(y = 2.3485x + 12855\) y obtenemos $48,082.50 para el modelo lineal.
Enchufe\(x = 15000\)\(y =-0.0006x^2 + 10.694x – 11586\text{,}\) y obtenemos $13, 824 para el modelo cuadrático.
[Puede usar Excel, una calculadora o Wolfram Alpha para hacer estos últimos cálculos.]
- Podemos hacer diagramas de dispersión y usar la línea de tendencia lineal para encontrar los modelos que necesitamos.
En la construcción de tanques de agua, las consideraciones de diseño indican que el peso del tanque seco debe ser aproximadamente una función de potencia de la capacidad. Me interesa construir un tanque más grande que el que tenía antes. Tengo los siguientes datos entre capacidad y peso:
| Galones | 1,000 | 5,000 | 7,000 | 9,000 | 17,000 |
| Peso | 103 | 878 | 1,339 | 1,927 | 4,496 |
- Encuentre la mejor función de potencia adecuada para los datos.
- Usa tu función de potencia para estimar el peso de un tanque que contiene 40,000 galones.
- Encuentre la función lineal que mejor se ajuste para los datos.
- Utilice su función lineal para estimar el peso de un tanque que contiene 40,000 galones.
- Visualmente, ambas curvas parecen encajar bastante bien en los datos, sin embargo, hacen notables predicciones diferentes para el peso de un tanque más grande. Qué predicción usarías. Justifica tu respuesta.
Estoy viendo cifras de ventas para un nuevo producto, el artilugio. Las cifras de ventas parecen estar creciendo a un ritmo exponencial.
| Mes | Ene | Abr | julio | Oct | Ene |
| Unidades vendidas | 1082 | 1680 | 2662 | 3783 | 6430 |
- Encuentre la función exponencial que mejor se ajuste a los datos.
- Usando su función, predice las ventas para el mes de julio después de que se recopilaron los datos.
- Contestar
-
- Usando el diagrama de dispersión y la línea de tendencia del menú Gráfico, elegimos Línea de tendencia exponencial y mostramos la función. Tenga en cuenta que sí necesitamos cambiar los meses al valor numérico apropiado. Excel simplemente los reemplazaría por números consecutivos.

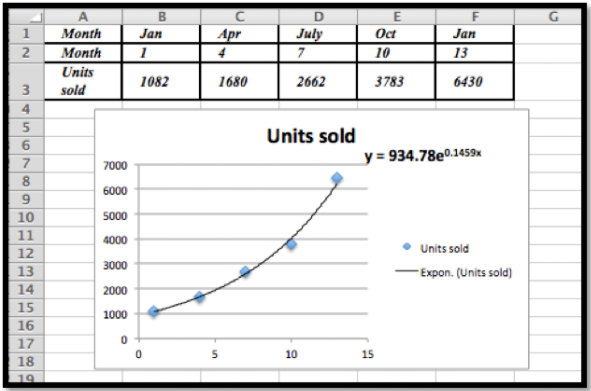
La curva exponencial de mejor ajuste dada por Trendlines es\(y = 934.78e^{0.1459x}\)
- Para encontrar las unidades previstas vendidas para julio necesitaríamos\(x = 19\text{.}\)

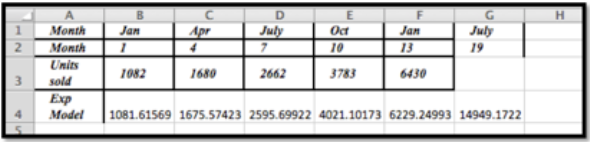
Usando Excel vemos que el número previsto de unidades vendidas es de 14.949.
- Usando el diagrama de dispersión y la línea de tendencia del menú Gráfico, elegimos Línea de tendencia exponencial y mostramos la función. Tenga en cuenta que sí necesitamos cambiar los meses al valor numérico apropiado. Excel simplemente los reemplazaría por números consecutivos.
- Excel tiene un conjunto limitado de modelos que se pueden usar para que las líneas de tendencia ajusten automáticamente las curvas a los datos. En secciones posteriores veremos cómo podemos usar el cálculo para encontrar las curvas que mejor se ajusten para otros modelos. Hasta que desarrollemos esas técnicas, podemos hacer una conjetura en los parámetros que harán que las curvas encajen.
Se puede esperar que las ventas unitarias de widgets sigan un modelo logístico, con un rápido crecimiento de las ventas, pero con eventual saturación del mercado para que haya un tope en el mercado. En tal caso las ventas deben ser modeladas por una ecuación logística, de la forma\(sales(time)=MarketCap/(1+adjustment*exp(-rate*time)).\) Tenemos los siguientes datos sobre ventas:
| tiempo (años) | 0 | 2 | 4 | 6 | 8 |
| ventas | 1000 | 5610 | 14,845 | 19.095 | 19,870 |
Encuentre valores de los parámetros MarketCap, ajuste y tasa para que se ajusten razonablemente a los datos.
Se puede esperar que las ventas unitarias de una prenda de ropa para adultos sigan el modelo de una distribución normal. En tal caso las ventas deben modelarse por una ecuación normal, de la forma
\[ sales(size)=MaxPerSize*exp\left(-\left(\left(\frac{size-Mean}{StandardDeviation}\right)^2\right)\right).\text{.} \nonumber \]
(Tenga en cuenta que necesitamos un conjunto adicional de paréntesis para mantener correcto el orden de las operaciones). Tenemos los siguientes datos sobre ventas:
| tamaño | 7 | 8 | 9 | 10 | 11 | 12 |
| Peso | 360 | 3,390 | 12,820 | 20,000 | 12,826 | 3,375 |
Encuentre los valores de los parámetros MaxPerSize, Mean y StandardDeviation para que se ajusten razonablemente a los datos.
- Contestar
-
La gráfica inicial muestra que la distribución es normal:

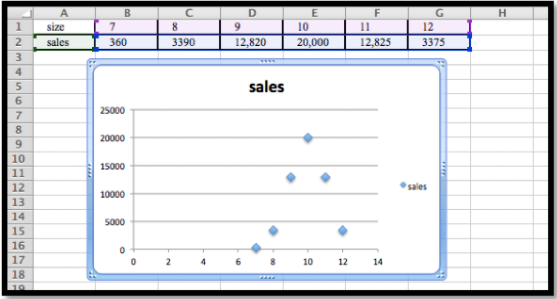
El máximo está en\(x = 10\text{.}\) Esto sugiere que\(Mean = 10\text{.}\)
Si usamos\(Sales (x)= MaxPerSize*e^{-\left(\left(\frac{x-10}{STDev}\right)^2 \right)}\text{,}\) entonces si\(x = 10\) tenemos\(Sales (10)= MaxPerSize\text{,}\) y así de\(MaxPerSize = 20,000\text{,}\) ahí tenemos eso
\[ Sales (x)= 20,000*e^{-\left(\left(\frac{x-10}{STDev}\right)^2 \right)}\text{.} \nonumber \]
Vamos\(x = 11\text{,}\) entonces\(12825= 20,000*e^{\left(\left(\frac{-1}{STDev}\right)^2 \right)}\text{.}\)
De ahí\(e^{\frac{-1}{STDev^2}}=frac{12825}{2000}. Then\)\(\frac{-}{STDev^2}=\ln\left(frac{12825}{20000}\right)\)
Así\(STDev= \sqrt{(-1/\ln(12825/20000 ) )}=1.5002\) que\(STDev= 1.5002\)
Comentario: Desarrollaremos algunos métodos para resolver problemas como este usando Excel en una sección llamada Best Fit Curves (Capítulo 6)
Las poblaciones de los estados se pueden encontrar en línea para los censos de 2000 y 2010. (Un buen sitio es http://en.Wikipedia.org/wiki/List_of_U.S._states_and_territories_by_population.)
- Explicar por qué se podría adivinar que la población 2010 de un estado es aproximadamente una función lineal de la población del año 2000 del estado.
- Descarga las poblaciones 2000 y 2010 de los 50 estados. Producir una gráfica de dispersión que tenga a la población de 2010 en función de la población del 2000. Encuentre la ecuación de una curva de mejor ajuste para los datos.
- Explique lo que significa la intercepción y en términos de personas que se mueven hacia o lejos de estados con grandes poblaciones.
Los ingresos fiscales de los estados se pueden encontrar en línea. (Un buen sitio es la oficina del censo en http://www.census.gov/govs/state/.)
- Explicar por qué se adivinaría que los ingresos fiscales de 2010 de un estado son aproximadamente una función lineal de la población 2010 del estado.
- Para 10 estados, producir un diagrama de dispersión que tenga los ingresos fiscales de 2010 en función de la población de 2010. Encuentre la ecuación de una curva de mejor ajuste para los datos.
- Explique qué significa la intercepción y en términos de la relación del tamaño del estado y la carga fiscal por persona.
Proyectos:
Encuentre los datos del índice de precios al consumidor y el promedio de Dow Jones Industrial al inicio del año de los últimos 50 años. A lo largo de ese tiempo, ¿cuál es la mejor relación lineal entre los dos índices? Para que tu ecuación sea más fácil de entender, escala los índices para que ambos comiencen a 100 el mismo día.
Elige tus dos acciones favoritas y grafica sus precios en los días de apertura por un periodo de 30 años. ¿Qué tan bien se modelan sus precios como un modelo lineal el uno del otro? A ver si puede encontrar dos acciones que parecen ser inversamente proporcionales entre sí.


