2.1: Problemas de equilibrio del mercado

Última actualización
Guardar como PDF

Page ID: 115951

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Como mencionamos en el capítulo anterior, muchas funciones son localmente lineales, por lo que si restringimos el dominio la función aparecerá lineal. Así, a menudo comenzamos con modelos lineales cuando tratamos de entender una situación. En esta sección analizamos los conceptos de oferta y demanda y equilibrio del mercado. Para nuestros ejemplos en esta sección asumiremos que las funciones son lineales en el rango que nos importa.

Oferta y Demanda y Equilibrio de Mercado.

Las leyes normales de la oferta y la demanda asumen que estamos en un mercado con muchos productores y consumidores, operando de manera independiente, todos ellos velando por sus propios intereses. Esperamos que cuando el precio suba, más productores estén dispuestos a vender pero menos consumidores estén dispuestos a comprar. Por el contrario, cuando el precio baja, menos productores están dispuestos a vender pero más consumidores están dispuestos a comprar.

Considera el ejemplo de los precios de la gasolina. Diferentes precios harán que algunas áreas de exploración y producción sean rentables o no rentables. Cuando los precios suben, se perforan nuevos pozos. Si los precios bajan demasiado, los pozos stripper dejan de ser rentables y se cierran. Desde el lado del consumidor, cuando los precios suben, más personas miran el transporte masivo o conseguir un vehículo más eficiente en combustible. Cuando bajan los precios, es más fácil pensar en un viaje por carretera.

La ley de abasto mira la economía desde el punto de vista del proveedor. Precio y cantidad disponible para la venta siempre se mueven en la misma dirección. Si el precio sube podemos suponer que todos los proveedores antiguos siguen dispuestos a vender al precio más alto, pero algunos proveedores más pueden ingresar al mercado. Si el precio baja, no entrarán nuevos proveedores al mercado, y algunos proveedores antiguos pueden salir del mercado. Para un modelo lineal:

\[ \text{slope of supply curve} = \frac{\text{change in price}}{\text{change in quantity supplied}} = \frac{\Delta p}{\Delta q} \gt 0\text{.} \nonumber \]

La ley de la demanda mira a la economía desde el punto de vista del consumidor. Precio y cantidad disponible para la venta siempre se mueven en sentido contrario. Si el precio baja podemos suponer que todos los viejos consumidores siguen dispuestos a comprar al precio más bajo, pero algunos consumidores más pueden ingresar al mercado. Si el precio sube, no entrarán nuevos consumidores al mercado, y algunos viejos consumidores pueden salir del mercado. Para un modelo lineal:

\[ \text{slope of demand curve} = \frac{\text{change in price}}{\text{change in quantity demanded}}= \frac{\Delta p}{\Delta q} \lt 0\text{.} \nonumber \]

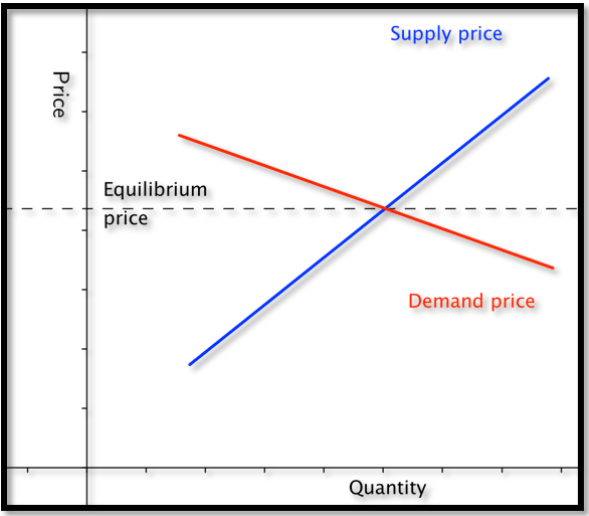
Cuando miramos una gráfica de la gráfica de precios de oferta y la gráfica de precios de demanda en la misma gráfica, sabemos que la curva de oferta sube a medida que vamos de izquierda a derecha, mientras que la curva de demanda baja. Por las propiedades de las líneas sabemos que hay un solo punto donde tal par de líneas puede cruzarse. Es en el punto donde la cantidad de bienes ofrecidos por un precio es igual a la cantidad de bienes deseados por el mismo precio.

Esta intersección de las funciones oferta y demanda se denomina punto de equilibrio del mercado, o punto de equilibrio.
El precio en este punto se conoce como el precio de equilibrio.
La teoría económica estándar dice que un mercado libre y abierto se asentará naturalmente en el precio de equilibrio.

$clipboard_ea04b871f8fb57a49836c36a98d714948.png$

Ejemplo 2.1.1: Comenzando con fórmulas.

Figura$2.1.2.$ Video presentación de este ejemplo

Supongamos que$q$ denota cantidad, y el precio de suministro para los widgets viene dado por

\[ \text{Supply price} =\$6+\frac{q}{100}\text{.} \nonumber \]

También nos dicen que el precio de la demanda viene dado por

\[ Demand \ price=\$18-\frac{2q}{100}\text{.} \nonumber \]

Encuentra el precio y la cantidad de equilibrio.

Solución

Solución. 1 (a)

Hemos comenzado con un ejemplo que podemos hacer por álgebra básica sin ninguna tecnología. Al restar las dos ecuaciones, vemos que

\[ 0=\$12-\frac{3q}{100}\text{.} \nonumber \]

Algún álgebra sencilla muestra que la cantidad de equilibrio es de 400. Sustituir de nuevo en cualquiera de las dos ecuaciones da un precio de equilibrio de $10.

Solución. 2 b

Si bien podemos hacer este ejemplo a mano, también queremos usarlo para configurar una solución con Excel, ya que es posible que queramos ayuda en problemas donde los números no son tan agradables. Nuestro plan es usar Goal Seek para encontrar la intersección. Necesitamos una celda donde podamos resolver el problema obligando a la celda a tener un valor de cero.

$clipboard_e66c52c1f0a7ddee1df278777c08c8f7c.png$

Cuando la celda D2 es cero, el precio de oferta será el mismo que el precio de demanda. Ahora invocamos Goal Seek.

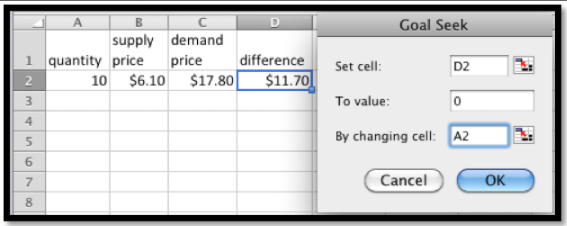
$clipboard_e3c1ec5d65b95fbe328fb5cf82b7ea83a.png$

Como era de esperar, encuentra equilibrio cuando$q=400\text{.}$

Tenemos que hacer un poco más de trabajo cuando simplemente se nos dan puntos de datos y necesitamos encontrar las curvas de oferta y demanda.

Ejemplo 2.1.3: Comenzando con Datos.

Figura$2.1.4.$ Video presentación de este ejemplo

Mis datos de mercado indican que los clientes comprarán 700 artilugios si tienen un precio de 13 dólares cada uno. Si el precio sube a 15 dólares, solo comprarán 500. Si el precio es de 12 dólares la unidad, los productores harán 400 gizmos. Si el precio sube a 13 dólares, producirán 600 aparatos. Supongamos que las curvas de oferta y demanda son lineales para entre 300 y 1000 artilugios. Encuentra el punto de equilibrio para el mercado de los gizmo.

Solución

Comenzamos haciendo un gráfico para los valores dados. Agregamos una gráfica de dispersión para que podamos ver los valores.

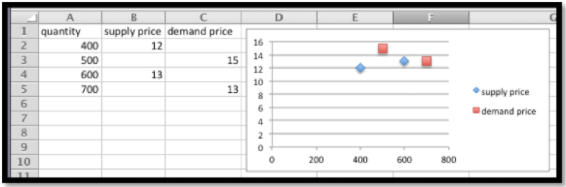
$clipboard_ee372ea4ea89b379c445c52e9ededa7dd.png$

A continuación agregamos líneas de tendencia lineales tanto para la oferta como para la demanda. Seleccionamos la opción para mostrar las ecuaciones.

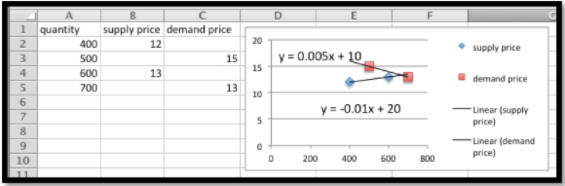
$clipboard_ec68c83fe637170b412a2c98278e668c0.png$

Las ecuaciones proyectadas son:

\ begin {align*}\ text {precio de oferta}\ amp =0.005*\ texto {cantidad} +10\\\ texto {precio de demanda}\ amp =-0.01*\ texto {cantidad} +20\ texto {.} \ end {alinear*}

Establecimos columnas para las curvas de oferta y demanda proyectadas. También agregamos una columna para la diferencia para que podamos usar Objetivo buscar para encontrar el punto de equilibrio.

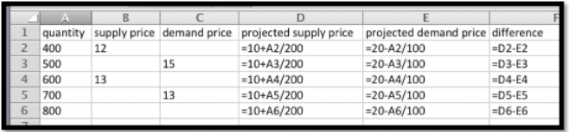
$clipboard_ebaa379f204638306a60b796e2aa46a7a.png$

Entonces es sencillo ver que la cantidad de equilibrio es 666.67 y el precio de equilibrio es de 13.33 dólares.

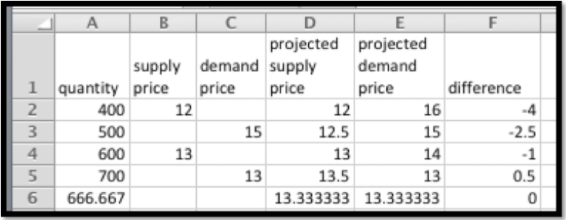
$clipboard_eb150fc25f98fa298c5e2081e2e889784.png$

Hay un detalle más digno de destacar de este último ejemplo. Dependiendo de las unidades utilizadas, la pendiente puede ser muy cercana a cero. Si estamos vendiendo decenas de millones de unidades por un precio inferior a un dólar, el cambio en el precio de un centavo puede corresponder a un cambio en cantidad de varios miles. Asegúrate de incluir suficientes dígitos para que tu ecuación sea significativa.

Ejemplo 2.1.5: Ventas de Computación.

Figura$2.1.6.$ Video presentación de este ejemplo

Hemos obtenido los siguientes datos para ventas de artilugios en nuestra ubicación.

cantidad	653	762	847	943	1050	1130	1260
Precio de la oferta	5.52		6.20		6.85		7.48
Precio de demanda		6.68		6.50	6.38	6.31

Supongamos que las curvas de oferta y demanda son lineales para cantidades entre 600 y 1300. Encuentre las mejores líneas de ajuste para las funciones de oferta y demanda. Encuentra el punto de equilibrio. Haz un gráfico con el listado de cuántos podemos vender por $6.40 y $6.60. Recuerde que las ventas serán el mínimo de la oferta y la demanda.

Solución

Comenzamos por poner los datos en una hoja de cálculo y encontrar las mejores líneas de ajuste. Seleccionamos la opción para mostrar las ecuaciones en el gráfico.

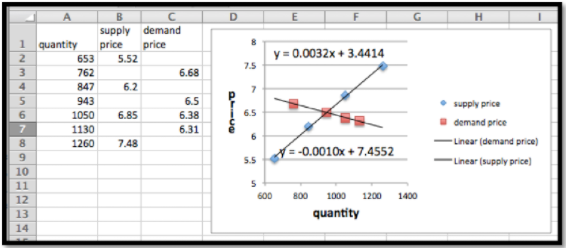
$clipboard_eef06c23d28ef9e0378145cdfda16634e.png$

Las funciones de oferta y demanda son:

\ begin {align*}\ text {precio de oferta}\ amp =.0032*\ texto {cantidad} +3.44\\ demanda\ precio\ amp =-0.0010*cantidad+7.46\ text {.} \ end {alinear*}

Agregamos columnas para los precios proyectados de oferta y demanda, utilizando las ecuaciones obtenidas a partir de las líneas de mejor ajuste. También agregamos una columna, y calculamos la diferencia de las funciones de oferta y demanda. Ahora podemos usar la búsqueda de objetivos para resolver el problema.

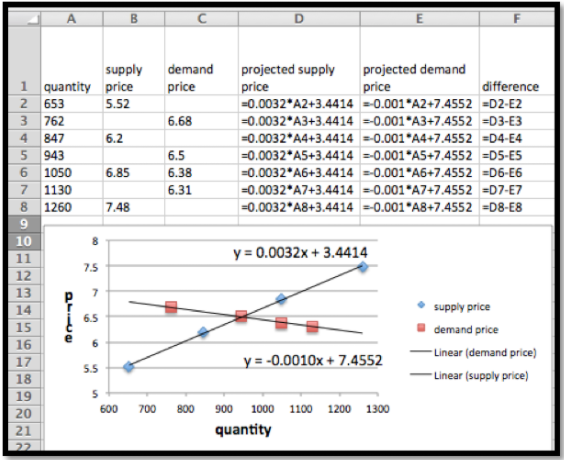
$clipboard_e5eb6c58287bddaaea2d877d24455fcf7.png$

Ahora usamos Goal Seek para encontrar el punto de equilibrio.

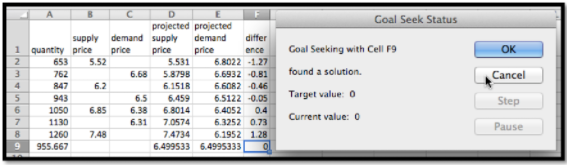
$clipboard_ec747ebc46cee03afbe61f0635c198161.png$

En equilibrio vendemos 956 gizmos a $6.50. Para encontrar ventas a $6.40 y $6.60, utilizamos Goal Seek para obtener esos valores tanto a precios de oferta como de demanda.

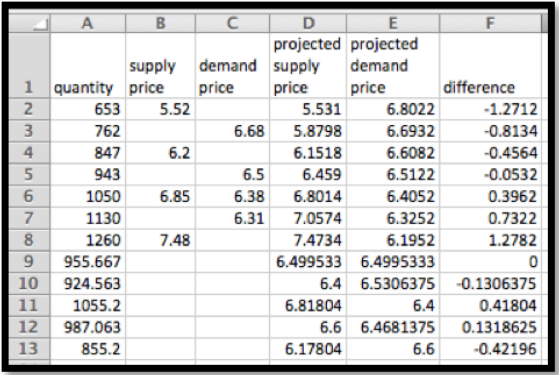
$clipboard_e642e257f5598a6d45379064e8e145c7a.png$

Vemos que podemos vender 1055 aparatos a $6.40, pero sólo podemos obtener 925. Así nuestras ventas a $6.40 serán de 925. A $6.60 podemos obtener 987 aparatos, pero sólo podemos vender 855. Así nuestras ventas a $6.60 serán 855. Podemos eliminar un paso en este proceso si recordamos que por debajo del precio de equilibrio la restricción es la oferta, mientras que por encima del precio de equilibrio la restricción será la demanda.

clase=”

Ejercicios 2.1 Problemas de equilibrio

Para los problemas 1-4, dadas las ecuaciones de las curvas de oferta y demanda:

Evaluar las curvas en$q_0\text{.}$
Encuentra el equilibrio del mercado.

Ejercicio 1:

Dado$supply\ price=3 quantity+10$ y$demand\ price=-2 quantity+30\text{,}$ con$q_0=6\text{.}$

Contestar

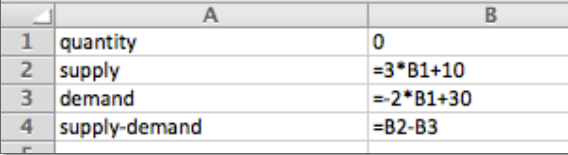
$clipboard_e27d0af61e0cc01fbbd9009a644d47f06.png$

Entradas en las celdas antes del llenado rápido

$clipboard_ed98a38b3a734cdb9f5869b4112723641.png$

Tabla con cantidades que van de 0 a 10

De la mesa vemos que al precio$q_0=6$ de oferta es de 28 dólares y el precio de demanda es de 18 dólares.