2.2: Funciones no lineales
- Page ID
- 115955
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Para la mayor parte de este capítulo nos hemos restringido a funciones que eran funciones lineales o funciones polinómicas donde se construyen a partir de la interacción de funciones lineales. Si bien esto hace que los modelos económicos sean más fáciles de entender, es bastante claro que las situaciones que nos importan suelen ser mejor descritas por funciones más complicadas. Los proveedores de gasolina tienen una cantidad finita que pueden entregar independientemente del precio. Eso lleva a una función de suministro muy no lineal. Vale la pena revisar cómo entraríamos otras funciones en una hoja de cálculo.
Funciones algebraicas.
Comenzamos con las funciones algebraicas que deberían ser familiares de cursos anteriores. Estas funciones nos permitirán utilizar todos los modelos que se mencionaron en el Capítulo 1. Para esta tabla, asumiremos que la entrada a la función se ha almacenado en la celda A1.
| Entrada Algebraica | Entrada de hoja de cálculo | Notas |
| \(f(x)=\sqrt{2x+7}\) | =SQRT (2*A1+7) |
* necesario para la multipliciación |
| \(f(x)=\sqrt[3]{2x+7}\) | =( 2*A1+7) ^ (1/3) |
otras raíces hechas como exponentes fraccionarios |
| \(f(x)=x^4\) | =A1^4 |
|
| \(f(x)=-x^4\) | =- (A1^4) |
Excel hace negación antes de exponenciación |
| \(f(x)=\ln(x)\) | =LN (A1) |
Base de tronco\(e\) o tronco natural |
| \(f(x)=\log_{10}(x)\) | =LOG10 (A1) |
Base de registro 10 o tronco común |
| \(f(x)=\log_{2}(x)\) | =LOG (A1,2) |
Log a otra base |
| \(f(x)=1.06^x\) | =1.06^ (A1) |
|
| \(f(x)=e^x\) | =EXP (A1) |
|
| \(f(x)=e^{(-x^2)}\) | =EXP (- (A1^2)) |
Paréntesis necesarios para una correcta evaluación |
| \(f(x)=|x|\) | =ABS (A1) |
Valor absoluto |
Considera una función de demanda y por qué probablemente no sea lineal. Esperamos que la demanda suba cada vez que bajemos el precio. Sin embargo con una función lineal, obtenemos el mismo incremento en la demanda al recortar el precio a la mitad, o si a partir de la mitad de precio regalamos el producto de forma gratuita. Un modelo más razonable puede ser una función de potencia donde disminuir el precio en un porcentaje fijo aumenta el consumo en un porcentaje fijo. De manera similar, cuando pensamos en la función de suministro, a menudo esperamos que los límites en los materiales disponibles hagan que el aumento del suministro sea progresivamente más caro.
Figura\(2.3.2.\) Video presentación de este ejemplo
Estamos interesados en vender artilugios. Lo máximo que pagará un consumidor es de $1,000. Si bajamos el costo en un 10% aumentamos la demanda en 100. El más barato por el que venderá un proveedor es de $200. Encontramos que el mercado producirá otros 100 artilugios cada vez que aumentemos el precio en un 20%. Encuentra el equilibrio del mercado.
Solución
Comenzamos convirtiendo nuestra información sobre la oferta y la demanda en ecuaciones, enchufando las ecuaciones en Excel y dibujando una gráfica. Luego usamos Goal Seek para encontrar dónde son iguales las dos ecuaciones.
\ begin {align*}\ text {Precio de Demanda} (\ text {cantidad})\ amp =1000* (0.9) ^ {(\ text {cantidad} /100)}\\\ text {Precio de Abastecimiento} (\ text {cantidad})\ amp =200* (1.2) ^ {(\ text {cantidad} /100)}\ text {.} \ end {alinear*}

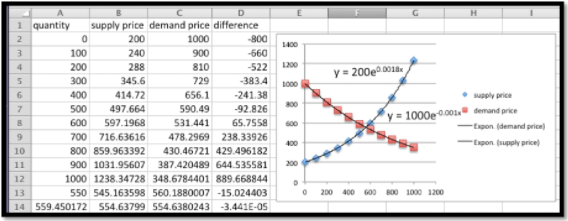
Vemos que el precio de equilibrio está en 554.64 dólares. A ese precio la oferta y la demanda serán ambas 559.45.
Figura\(2.3.4.\) Video presentación de este ejemplo
Tenemos la siguiente tabla de datos para el precio de demanda y costos de nuestro producto.
| Cantidad | 100 | 300 | 500 | 1000 | 1500 |
| Precio de Demanda | $35.35 | $21.63 | $17.25 | $12.70 | $10.26 |
| Costos | 2347.67 | $5040.00 | 7481.67 | $12469.67 | $16196.00 |
Tenemos razones para creer que mi precio de demanda es una función de poder de algún tipo. Nuestra función de costo es cercana a la lineal, pero podemos obtener descuentos por volumen y reducir el costo por unidad con cantidades mayores. Así esperamos que mi función de costo sea en realidad cuadrática, con el término cuadrático mucho más pequeño que el término lineal. Encuentre las mejores curvas de ajuste por costo y precio. Derivar funciones para ingresos y ganancias. Encuentra puntos de equilibrio entre 10 y 1500.
Solución
Empiezo por encontrar curvas de mejor ajuste de costo y precio.

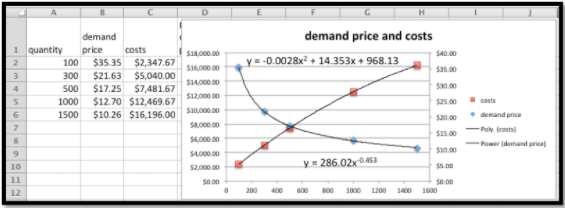
Así tenemos:
\ begin {align*}\ text {cost} (q)\ amp =-0.0028q^2+14.353q+968.13\\\ text {price} (q)\ amp =286.02 q^ {-0.453}\ text {.} \ end {alinear*}
A continuación, seguimos nuestros modelos para obtener ecuaciones de ingresos y ganancias.
\ begin {align*}\ text {revenue} (q)\ amp =q*\ text {price} (q) =q 286.02 q^ {-0.453} =286.02 q^ {0.547}\\ text {beneficio} (q)\ amp =\ text {ingresos} (q) -\ text {costo} (q) =286.02 q^ {0.547} +0.0028q^2-14.353q-968.13\ texto {.} \ end {alinear*}
Finalmente, cargamos estas ecuaciones de nuevo en Excel y usamos Goal Seek para encontrar los puntos de equilibrio. Al observar la ganancia proyectada en el gráfico vemos un cambio de señal cerca de 1000, por lo que sospechamos que hay un punto de equilibrio allí. También observamos que la ganancia parece estar subiendo hasta que\(q\) es de aproximadamente 300, así que pruebo para un punto de equilibrio para valores pequeños de\(q\text{.}\)

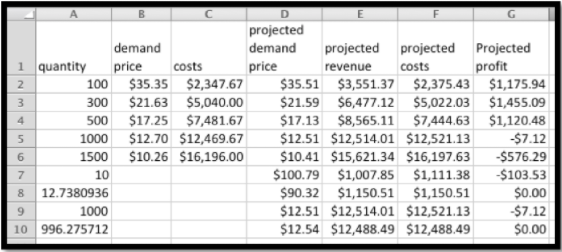
Vemos que tenemos puntos de equilibrio cuando q es 12.74 y 996.28.
Funciones Discontinuas.
Todas las funciones anteriores tienen gráficas sin roturas. En términos matemáticos, son funciones continuas. Cuando estamos modelando fenómenos del mundo real, también queremos usar funciones que tengan rupturas en la gráfica. La pintura generalmente se compra en contenedores de galones, por lo que el precio para pintar una habitación se basa en el número de galones redondeados al siguiente número entero. Muchos negocios darán un descuento por volumen a sus mejores clientes, por lo que hay un precio por pequeñas cantidades y un precio diferente para grandes cantidades. El costo de la mano de obra cambia si se trata del pago de horas extras. En todos estos casos la gráfica tiene una ruptura en ella.
Excel tiene varias funciones discontinuas que nos son de utilidad.
| Función | Ejemplo | Valor | Notas |
| REDONDO | REDONDO (2.347,1) | 2.3 | 2.35 redondearía a 2.4 |
| REDONDEAR | REDONDEAR (2.99,0) | 2.0 | 0 para redondear dígitos a enteros |
| RESUMEN | ROUNDUP (-2.132,2) | -2.14 | Arriba está lejos de 0. |
| TECHO | TECHO (3.14159,1.5) | 4.5 | Redondea hasta un múltiplo de 1.5 |
| PISO | PISO (3.14159,2) | 2 | Redondea hacia abajo a un múltiplo de 2. |
| SI | SI (\(2 \lt 1\text{,}\)5,10) | 10 | La condición es falsa. |
| MIN | MIN (1, 3, 5) | 1 | El mínimo de una lista de valores. |
| MAX | MAX (1, 3, 5) | 5 | El máximo de una lista de valores. |
Las funciones REDONDO, REDONDO y REDONDO se utilizan para redondear. Tienen un segundo argumento que especifica el número de dígitos a los que estamos redondeando. Cabe señalar que Excel entiende arriba y abajo como lejos de cero para números negativos. Así redondeará\(-1.5\) hasta\(-2\text{.}\) Las funciones TECHO y PISO también hacen redondeo, pero con algunas características diferentes. En lugar de especificar el número de dígitos en la respuesta, estas funciones redondean a un múltiplo del segundo argumento. Como era de esperar, el TECHO redondea al siguiente múltiplo superior y el PISO redondea al siguiente múltiplo inferior. 
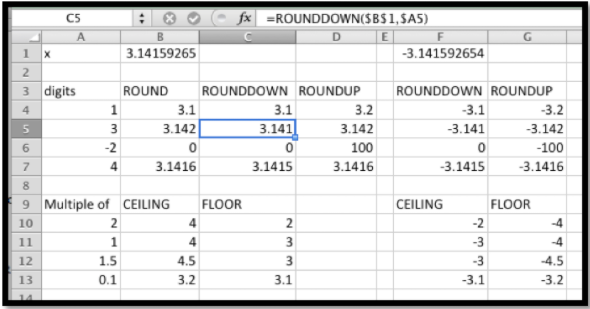
Figura\(2.3.5.\) Video discusión de funciones discontinuas en Excel
Figura\(2.3.7.\) Video presentación de este ejemplo
La materia prima necesaria para construir widgets se vende en bloques que harán 100 widgets. Un bloque cuesta $1000. El costo de mano de obra para construir un widget es de $7. Los costos fijos para la producción de widgets son de $10,000. Encuentre una fórmula para los costos de producción de widgets. Encuentra el costo de producir 998 y 1009 widgets. También debes encontrar el costo por unidad en esas cantidades.
Solución
Para facilitar el seguimiento de la hoja de trabajo, dividimos los costos en tres pedazos, los costos fijos de mano de obra y los costos de materiales. Las costas fijas son constantes y los costos de mano de obra son lineales. Para los costos de materiales necesitamos usar la función CEILING para redondear el número de widgets hasta los siguientes incluso 100, luego dividir por 100 para obtener el número de bloques de materia prima que queremos comprar.
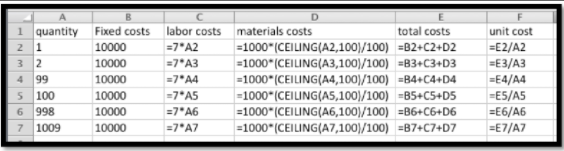
Cuando miramos los números vemos que el costo total de producir 998 widgets es de 26,986 dólares y el costo de producir 1009 widgets es de 28,063 dólares. Cuando miramos los costos unitarios, esperamos que el costo por unidad generalmente baje a medida que producimos más, ya que los costos fijos se distribuyen en más unidades. Sin embargo el costo por unidad es de $27.04 cuando producimos 998 widgets, pero eso sube a $28.81 cuando hacemos 1009 widgets, ya que tuvimos que comprar otro bloque de materia prima.
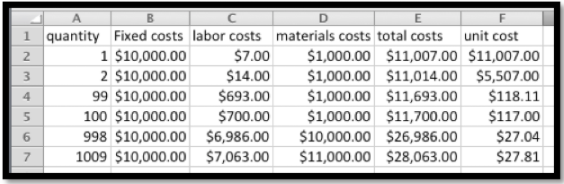
El comando IF se usa cuando usamos diferentes fórmulas para diferentes casos. Algunos ejemplos fáciles son el pago de horas extras, los costos de beneficios y el descuento por volumen. En muchas situaciones laborales a los empleados se les paga una tarifa hasta cierta cantidad de trabajo y una segunda tarifa por trabajo adicional. También es común que los empleados de tiempo completo reciban ciertos beneficios, como la jubilación, que no se ofrecen a los empleados a tiempo parcial. También es común que ciertas industrias ofrezcan diferentes tarifas para sus mayores y mejores clientes. La sintaxis básica del comando IF es:
IF (condición de prueba, valor si condición es verdadera, valor si condición es falsa)
Los valores para true y false pueden ser números, cadenas o fórmulas para evaluar.
Figura\(2.3.9.\) Video presentación de este ejemplo
Soy contable en una pequeña firma. La política de la empresa paga a los empleados tiempo y medio por trabajar más de 40 horas semanales. Necesito computar el pago semanal de 5 empleados. Los empleados trabajaron 35, 42, 43, 38 y 42.5 horas. Sus tarifas de pago base fueron respectivamente de $8, $9, $10, $11 y $12 por hora. Compute el pago de cada empleado.
Solución
Al configurar la hoja de trabajo, separaré el pago regular del pago de horas extras. El pago regular es la tarifa base multiplicada por las horas trabajadas, a menos que el empleado haya trabajado más de 40 horas, en cuyo caso es la tasa base multiplicada por 40. El pago de horas extras es el pago base multiplicado por 1.5 veces el número de horas extras. Dado que las horas extras no pueden ser negativas utilizamos el máximo de 0 y las horas trabajadas menos 40.
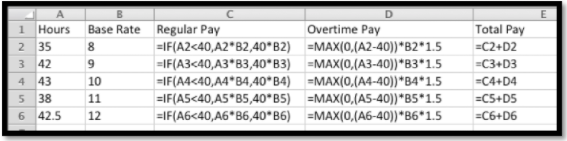
Al observar los valores calculados, a los empleados se les deben $280, $387, $445, $418 y 525 dólares, respectivamente.
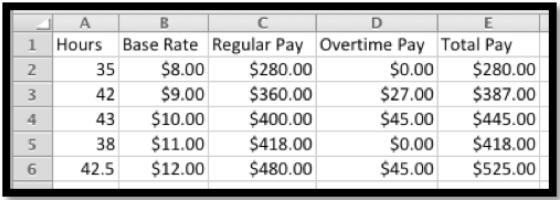
Si nuestras funciones son discontinuas, necesitamos tener un poco de cuidado con nuestros modelos económicos y los puntos de interés que hemos ido encontrando. El equilibrio del mercado y los puntos de equilibrio son ambos lugares donde dos funciones son iguales. Cuando las matemáticas no nos dan una respuesta clara debemos pensar en el problema y considerar qué respuesta tiene más sentido. Considera un ejemplo simplificado para ilustrar el punto.
Figura\(2.3.11.\) Video presentación de este ejemplo
En el mercado de widgets la oferta está restringida. Obtener más de 2 widgets significa utilizar un proceso más caro. Mis curvas de oferta y demanda son:
\ begin {align*}\ text {precio de demanda} (q) =4-q/2\\\ text {precio de oferta} (q) =\ begin {cases} 1q/2+1&q\ le 2\\ 1q/2+3&q>2\\\ end {cases}\ text {.} \ end {alinear*}
Encuentra el precio de equilibrio del mercado.
Solución
Nos gustaría encontrar el lugar donde se cruzan las dos curvas. Sin embargo cuando miramos una gráfica de las dos funciones vemos que nunca cumplen.
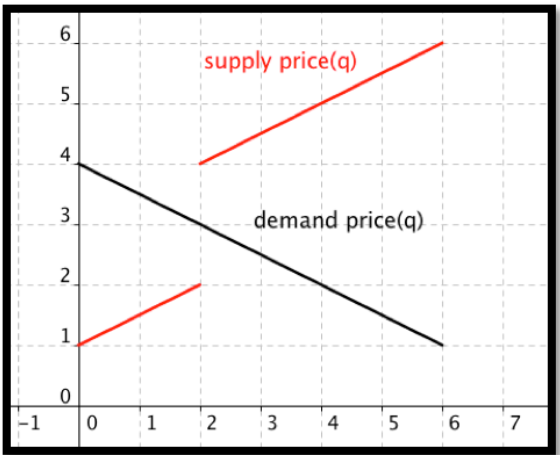
De la gráfica queda claro que el mercado debe alcanzar el equilibrio en una cantidad de 2, pero no está claro cuál debe ser el precio de equilibrio. Necesitamos hacer algún razonamiento sobre el comportamiento descrito por las ecuaciones. De nuestra fórmula, el precio de suministro para 2 widgets es de $2. No obstante si miramos los precios de oferta de\(2+h\) para valores pequeños de\(h\text{,}\) vemos que el límite del precio de suministro desde arriba es de 4 dólares. En términos prácticos los proveedores producirán 2 widgets por cualquier precio de $2 a $4. Si ofrecemos $2, también están dispuestos a producir 2 widgets. Si ofrecemos un precio de $3.95, todavía solo están dispuestos a producir 2 widgets. Los proveedores estarán así dispuestos a producir 2 widgets a un precio de $3. El precio de equilibrio es 3.
Si queremos mirar la gráfica en Excel, es útil trazar puntos muy cercanos a la discontinuidad en ambos lados. Para este problema, podríamos mirar tanto el 2 como el 2.0001.
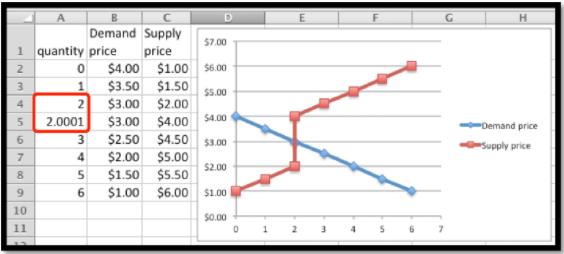
Una lección para recordar es que debemos prestar atención a los lugares donde nuestras funciones son discontinuas y que necesitamos entender qué debe hacer nuestro modelo económico cuando las curvas no se cruzan. Por ejemplo, entenderemos que el punto de equilibrio es el primer punto en el que los ingresos son mayores o iguales a los costos. En el caso continuo, esto se reduce a nuestra vieja definición.
clase=”Ejercicios Ejercicios 2.3 Funciones no lineales
- Para Ejercicio\(2.3.1–2.3.5\), dadas las ecuaciones de las curvas de oferta y demanda:
- Evaluar las curvas en\(q_0\text{.}\)
- Encuentra el equilibrio del mercado.
Dado\(\text{supply price}=20*(1.1)^{(q/10)}\) y\(\text{demand\ price}=50*(0.95)^{(q/10)}\text{,}\) con\(q_0=10\text{.}\)
- Contestar
-

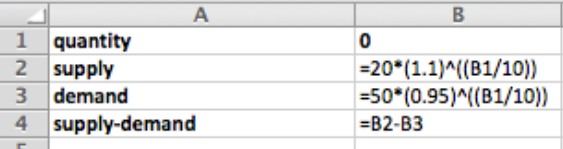
Fórmulas


Mesa
- A la\(q_0=10\text{,}\) oferta = $22, y demanda = $47.50
- Usando Goal Seek vemos que el equilibrio ocurre en\(q = 62.5\) y el precio es de $36.29
Suministro dado\(\text{price}=10*(1.05)^{(q/10)}\) y\(\text{demand price}=60*(0.96)^{(q/10)}\text{,}\) con\(q_0=10\text{.}\)
Dado\(p_s=5 \ln(q+10)\) y\(p_d=1000/(q+10)-2\text{,}\) con\(q_0=40\text{.}\)
- Contestar
-

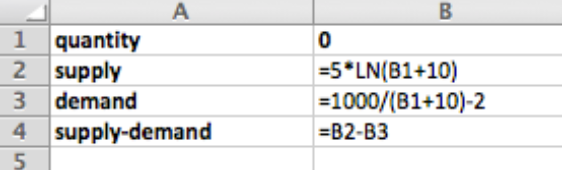
Fórmulas


Mesa


Goal Seek cerca\(q=40\)
- A la\(q_0=40\text{,}\) oferta = $19.56, y demanda = $18
- Usando Goal Seek vemos que el equilibrio ocurre en\(q = 37\) y el precio es de $19.25
Dado\(supply\ price=10 \ln(q+2)\) y\(demand\ price=60*(0.90)^{(q/100)}\text{,}\) con\(q_0=6000\text{.}\)
Dado
\[ \text{supply price}(q)=\begin{cases} 20*(1.1)^{(q/10)}&q \le 50\\ 20*(1.1)^{(q/10)}&q \gt 50\\ \end{cases} \nonumber \]
y
\[ \text{demand price}(q)=50*(0.095)^{(q/10)}\text{,} \nonumber \]
con\(q_0=40\text{.}\)
- Contestar
-
Para este problema nuestra función de precio de oferta cambia en\(q = 50\text{.}\) Esto se indica en la tabla por una delgada columna azul.


- A la\(q_0=40\text{,}\) oferta = $29.28, y demanda = $40.73
- El equilibrio ocurre en algún lugar entre\(q = 60\) y\(q = 70\text{.}\) Usando Goal Seek encontramos que el equilibrio ocurre para\(q = 62.43\)
- Para Ejercicio\(2.3.6–2.3.8\), dados los datos de oferta y demanda:
- Encuentre las ecuaciones de mejor ajuste de las curvas de oferta y demanda, utilizando los supuestos dados en el problema.
- Encuentra el equilibrio del mercado.
- Encuentre los precios de oferta y demanda proyectados para las cantidades adicionales dadas.
Dados los datos
| Cantidad | 100 | 120 | 140 | 160 | 180 | 155 |
| Precio de la oferta | 32 | 35.5 | 39 | 42.6 | 47 | |
| Precio de demanda | 47.2 | 42.5 | 38.3 | 34.5 | 31 |
y la suposición de que el precio de oferta y el precio de demanda son ambos exponenciales.
Dados los datos
| Cantidad | 5017 | 5937 | 7003 | 8070 | 9017 | 9943 | 7500 |
| Precio de la oferta | 17.5 | 19 | 20.4 | 23.7 | 25.1 | ||
| Precio de demanda | 29.6 | 26.7 | 21.3 | 19.2 | 17.6 |
y la suposición de que el precio de oferta es lineal y el precio de demanda es exponencial.
- Contestar
-

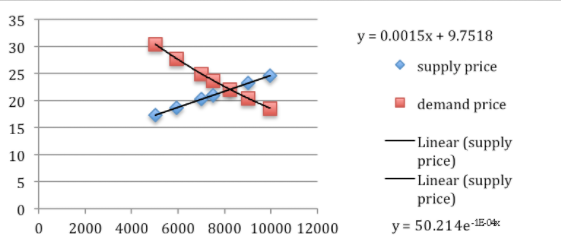
- Usando la función de línea de tendencia de Excel obtenemos eso
\ begin {align*}\ text {Abastecimiento}\ amp= 0.0015x + 9.7518\\\ text {Demanda}\ amp = 50.214e^ {(-0.0001x)}\ text {.} \ end {alinear*}
- Consulte las tablas a continuación.
- Consulte las tablas a continuación.

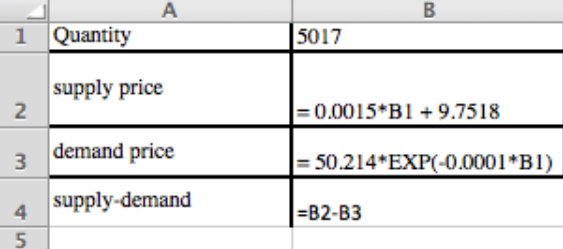
Fórmulas ingresadas

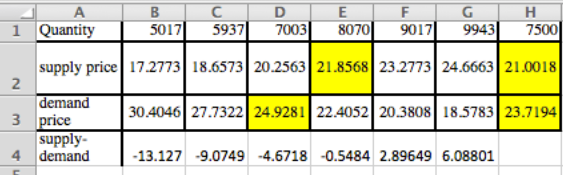
Encontrar a todos los valuadores con estas fórmulas. Los amarillos son los que estamos buscando.

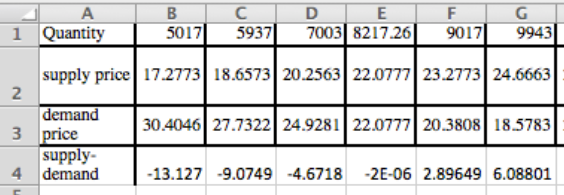
Usando Goal Seek para encontrar los valores de equilibrio en la columna E
- Usando la función de línea de tendencia de Excel obtenemos eso
Dados los datos
| Cantidad | 1009 | 1469 | 2041 | 2462 | 3002 | 3517 | 3979 | 3200 |
| Precio de la oferta | 98 | 106 | 112 | 120 | 1231 | 126 | ||
| Precio de demanda | 160 | 144 | 116 | 102 | 82 |
y la suposición de que el precio de oferta es lineal y el precio de demanda es exponencial.
- Para Ejercicio\(2.3.9–2.3.15\), para las funciones dadas:
- Dar el comando excel que producirá la siguiente función con el supuesto de que x está en la celda A2.
- Dar un gráfico de los valores de la función evaluada como x va de 0 a 100 en pasos de 5.
- Una gráfica de la función.
- Una lista de valores x donde la función es discontinua. (Donde salta la gráfica.)
Let
\[ f(x)=\begin{cases} \ln(2x)&x \le 50\\ 200\exp(-x/10)&x \gt 50\\ \end{cases}\text{.} \nonumber \]
- Contestar
-
- El comando de Excel es
=IF (A2 < =50, LN (2*A2) ,200*EXP (-A2/10)) - El gráfico es producido por el siguiente código.

- La gráfica se verá de la siguiente manera. Tenga en cuenta que la función no está definida en 0.

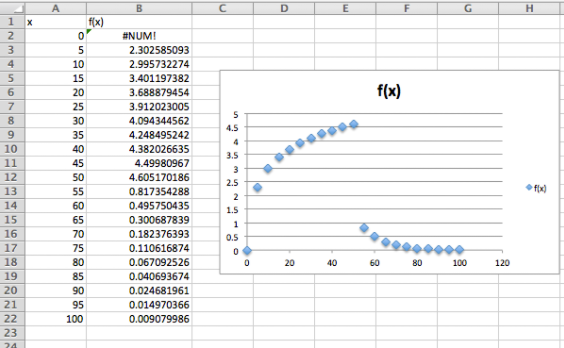
- La función no es continua en\(x = 50\text{.}\) Tenga en cuenta que la función cae de cerca de 4.5 a aproximadamente 1 bastante repentinamente.
- El comando de Excel es
Let
\[ f(x)=\begin{cases} \sqrt{2x+21}&x \le 50\\ 10\sin(x/5)&x \gt 50\\ \end{cases}\text{.} \nonumber \]
El costo de envío de un artículo es de $2 por libra, o fracción de la misma, con un costo mínimo de $5.
- Contestar
-
- La función es
=MAX (2*A2,5) -
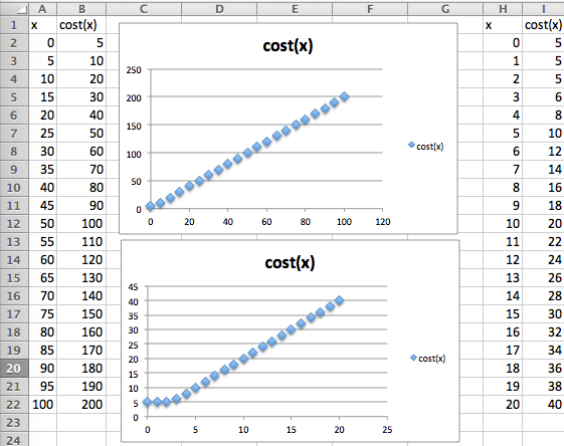

- La función es


