3.1: Funciones marginales y cocientes de diferencia

Última actualización
Guardar como PDF

Page ID: 116006

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay una serie de industrias donde es común que las personas paguen precios significativamente diferentes por el mismo producto del mismo proveedor. (Me vienen a la mente boletos de avión, asientos sinfonicos y donas en diferentes momentos del día). El motivo generalmente no es el favoritismo o un vendedor irracional, sino un análisis que analiza el cambio en costos y ganancias para realizar una venta adicional. Volar un avión con 51 pasajeros no cuesta mucho más que volar el mismo avión con 50 pasajeros. Lo mismo ocurre cuando se toca una sinfonía. Vender una dona extra a mitad de precio, justo antes de cerrar cuando tendrías que tirar la dona se suma a la ganancia. En todos estos casos, estamos menos preocupados por los ingresos y ganancias totales y más preocupados por cómo cambian las cosas con una venta más.

En finanzas y economía este tema se aborda utilizando funciones marginales.

Definición$3.1.1.$: Marginal value.

Si$f(x)$ es una función (es decir, costo, ingresos o ganancias), definimos el valor marginal de$f(x)$ ser el cambio en$f(x)$ como$x$ aumenta en 1. Así

\[ \operatorname{Marginal}f(x+1)=f(x+1)-f(x)\text{.} \nonumber \]

Vale la pena señalar un detalle que puede causar un poco de confusión. Tenga en cuenta que estamos definiendo funciones marginales de$x+1$ más que las funciones marginales de$x\text{.}$ Esta es la convención estándar en finanzas donde la pregunta se formula en términos de cambio asociado a producir una más. Me preocupa más decidir qué debo hacer en lugar de mirar lo que ya he hecho. Las funciones habituales con funciones marginales relacionadas son Costo, Ingresos y Ganancias.

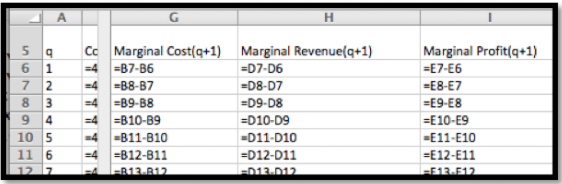
Costo Marginal en$x\text{,}$ o$\Mcost(x+1)$ es el cambio de$\cost(x)$ a$\cost(x+1)\text{:}$
\[ \Mcost(x+1)=\cost(x+1)-\cost(x)\text{.} \nonumber \]
$\Mrev(x+1)$es el cambio de$\revenue(x)$ a$\revenue(x+1)\text{:}$
\[ \Mrev(x+1)=\revenue(x+1)-\revenue(x)\text{.} \nonumber \]
$\Mprofit(x+1)$es el cambio de$\profit(x)$ a$\profit(x+1)\text{:}$
\[ \Mprofit(x+1)=\profit(x+1)-\profit(x)\text{.} \nonumber \]

Es de destacar que los tres ejemplos mencionados son todos casos en los que ya se ha establecido el costo de producción de los bienes, los bienes no se pueden guardar y vender posteriormente, y cualquier cambio en los ingresos se suma a la ganancia.

Ejemplo 3.1.2: Funciones Marginales para Widgets.

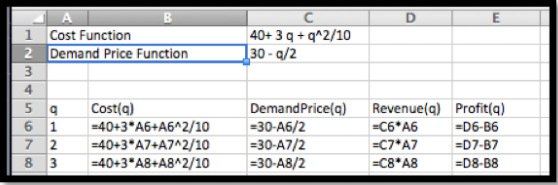
Para mi empresa de widgets he determinado que las funciones de costo y precio de demanda son:

\ begin {align*}\ cost (q)\ amp =40+3q+q^2/10\\\ Dprice (q)\ amp =30-q/2\ text {.} \ end {alinear*}

Quiero calcular el costo marginal, los ingresos y las ganancias para producir el widget 11 y 26. También quiero entender el costo marginal de producir el 1er widget.

Para configurar el problema recuerdo que suponemos que estamos vendiendo al precio de demanda, el precio más alto pagarán los consumidores y todavía nos harán vender todo lo que producimos. Así, las fórmulas para ingresos y ganancias son:

\ begin {align*}\ revenue (q)\ amp = (\ Dprice (q)) *q\\\ profit (q)\ amp =\ revenue (q) -\ cost (q). \ end {alinear*}

Configuré mi hoja de trabajo para calcular estos valores.

$clipboard_e548915b2f9ab14e4b7c5ac28c5076118.png$

Luego creo columnas adicionales para las funciones marginales.

$clipboard_e696923462b58df77dde205a65cf551d0.png$

Ahora simplemente volvemos a los valores y vemos los valores.

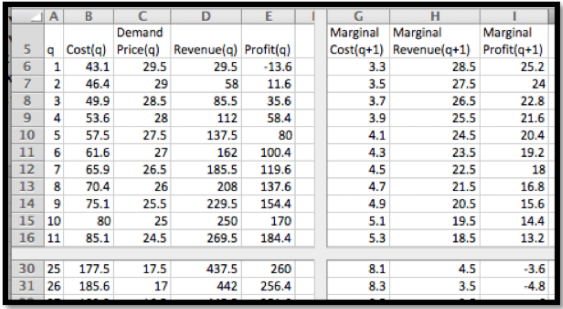
$clipboard_ecb981e0cb05a48bd7b5c65149a109ae3.png$

\ begin {align*}\ Mcost (11)\ amp =\ cost (11) -\ cost (10) =85.1-80=5.1\\\ Mrev (11)\ amp =\ revenue (11) -\ revenue (10) =269.5-250=19.5\\ Mprofit (11)\ amp =\ profit (11) -\ profit (10) =184.4-170=14.4\\\ amp\\ Mcosto (26)\ amp =\ costo (26) -\ costo (25) =185.6-177.5=8.1\\\ Mrev (26)\ amp =\ ingresos (26) -\ ingresos (25) =442-437.5=4.5\\ Mbeneficio (26)\ amp =\ beneficio (26) -\ beneficio (25) =256.4-260=-3.6\ text {.} \ end {alinear*}

La última ecuación ilustra el uso de funciones marginales. Si bien producir y vender el widget número 26 sí incrementó los ingresos totales, la ganancia marginal fue negativa, por lo que habría estado mejor si hubiera hecho menos widgets. Observe que el valor marginal de producir el primer widget no está en la hoja de cálculo y debe tratarse como un caso especial. Dadas nuestras funciones tenemos dos formas razonables de entender el valor$\cost(0)\text{.}$ O bien podemos asumir que no hay costo por no estar en un negocio, entonces$\cost(0)=0\text{,}$ y nuestra función de costo solo fue válida para números positivos, o que el$\cost(0)$ se entiende como los costos fijos, que ya tenemos emprendido, como un impuesto o tasa de licencia, así que$\cost(0)=40$ para este problema. Ambas son interpretaciones razonables. Habrá que mirar el contexto de nuestro problema para decidir sobre la correcta interpretación.

Muchas preguntas en los negocios pueden traducirse en hacer que alguna función sea lo más grande o pequeña posible, dependiendo de si pensamos que el valor es bueno o malo. Por lo tanto, a menudo es útil ver una gráfica tanto de la función de interés como de la función marginal relacionada en la misma gráfica.

Ejemplo 3.1.3: Ganancia y Beneficio Marginal Juntos.

Figura$3.1.4.$ Video presentación de este ejemplo

La función$\profit(q)=-q^2/20+100q-1000 $ expresa el beneficio en mi fábrica de gadgets. Trazar tanto el beneficio como el beneficio marginal juntos para estimar tanto la ganancia máxima en la fábrica, como la cantidad que debo producir para obtener esa ganancia.

Solución

Al configurar la hoja de cálculo, hay algunos detalles para notar.

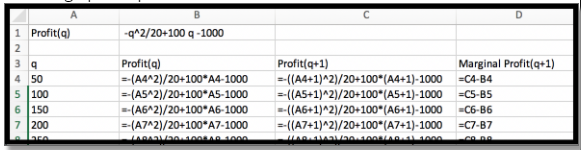
$clipboard_ecdd1fb02df0c755e0dd04c39950b7b66.png$

Ya que Excel hace negación ante poderes, necesito paréntesis por lo que$–(q^2)$ se evalúa correctamente. Ya que sospecho voy a tener que mirar un amplio rango de números para encontrar el máximo, pongo$\profit(q)$ y$\profit(q+1)$ como columnas separadas. Esto mantiene mi operación marginal en una sola fila y permite el cálculo de Beneficio Marginal sin evaluar por cada valor de q. Ahora miramos la gráfica con Beneficio y Beneficio Marginal. Para que la gráfica sea más fácil de leer, se utiliza un eje secundario con fines de lucro. Esto nos permite ver donde el Beneficio Marginal cruza el eje.

Vemos que el beneficio alcanza un máximo donde el beneficio marginal es cero. Esto ocurre aproximadamente cuando q es aproximadamente 1000. En ese caso la ganancia es de alrededor de 50 mil dólares. Mirando hacia atrás a los números en la hoja de cálculo, vemos que la ganancia máxima está más cerca de 49,000 dólares.

La situación más realista a la que nos enfrentamos es aquella en la que se nos da una recopilación de puntos de datos. En esa situación necesitamos primero encontrar una curva que mejor se ajuste y usarla para hacer valores predichos. Entonces podemos encontrar la función marginal de interés y hacer nuestra comparación.

Ejemplo 3.1.5: Beneficio Marginal de Datos.

Figura$3.1.6.$ Video presentación de este ejemplo

Tengo los siguientes datos sobre ganancias y nivel de producción para widgets.

Widgets producidos	40	50	78	87	95
Beneficio	$7,486.40	$14,505.60	23,431.60	23,014.30	21,258.50

Utilice Beneficio Marginal para encontrar el nivel de producción que maximice el beneficio.

Solución

Puse los datos en una hoja de cálculo y encuentro una curva que mejor se ajuste para producir una fórmula. Al mirar los datos, asumiré que el beneficio es una función cuadrática de la cantidad producida.

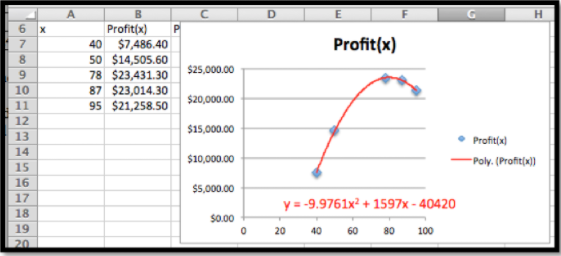
$clipboard_ef6d9c1635da4c0075efc2a7ec376540e.png$

Con la fórmula de la línea de tendencia puedo agregar una columna para$\Pprofit(x)\text{.}$ El ajuste$\Pprofit(x+1)\text{.}$ obvio produce Entonces es fácil calcular el valor de$\Mprofit(x+1)\text{.}$

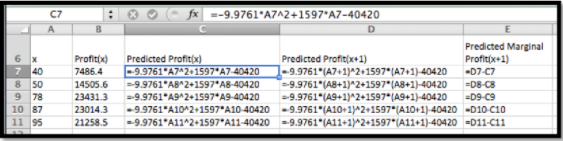
$clipboard_eca34b9973835774cd4910d3bcb7cd5f2.png$

Al mirar la gráfica, el máximo está cerca de simplemente$x=80\text{.}$ agrego algunas filas con valores apropiados de$x$ para obtener la respuesta deseada.

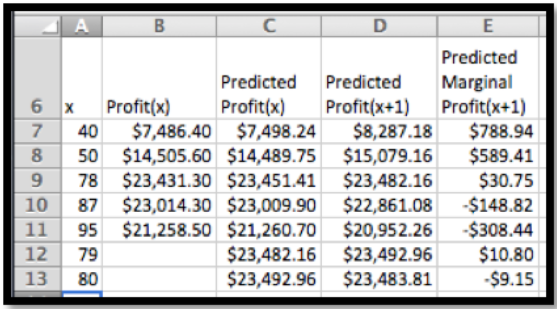
$clipboard_ec0b7219e58920ebaf16a55c4190121c0.png$

Cuando$x = 80\text{,}$ la Ganancia Marginal se vuelve negativa. El beneficio máximo es de $23,492.96, obtenido al producir 80 widgets.

Cocientes de Diferencia y Tasa Promedio de Cambio.

El valor marginal,$Mf(x+1)\text{,}$ de una función$f(x)\text{,}$ mide la cantidad de cambio de$f(x)$ a$f(x+1)\text{.}$ También puede entenderse como un caso especial de la tasa promedio de cambio de$f(x)\text{.}$

Es fácil ver que la tasa promedio de cambio de$f(x)$ como$x$ va de$a$ a$b$ es

\[ \frac{f(b)-f(a)}{b-a}\text{.} \nonumber \]

Hay una serie de situaciones en las que queremos mirar la tasa promedio de cambio para un periodo de algún otro cambio en la variable. Podemos tener producción en miles o millones de unidades. Si estamos buscando registros financieros mensuales o trimestrales, es posible que queramos ver la tasa promedio de cambio a lo largo de un año para tener en cuenta la variación estacional de la producción.

Ejemplo 3.1.7: Tasa de cambio cuando el denominador no es 1.

Figura$3.1.8.$ Video presentación de este ejemplo

Tenemos los siguientes datos de ventas mensuales sobre artilugios.

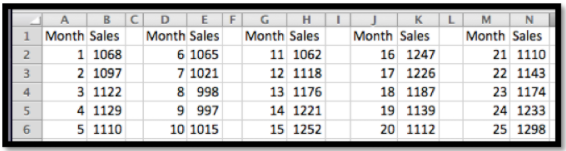
$clipboard_e7a29c4d0785039d0b6eb17a7a0c69c40.png$

Queremos encontrar la tasa de cambio de las ventas mensuales. Si miramos una gráfica de los datos de ventas:

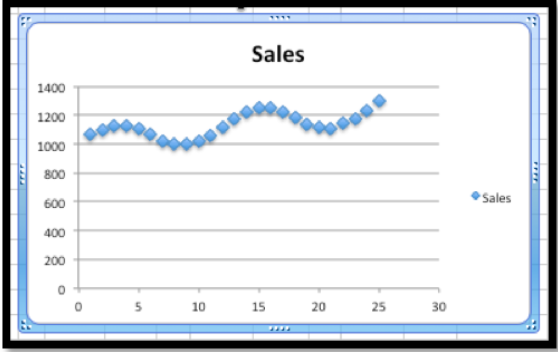
$clipboard_ef6b0add75b4fb7b9b61d4b18e51d7add.png$

Puedo ver que las ventas tienden al alza, pero hay una variación estacional agregada en. Excel no hará un buen trabajo modelando esta función con una línea de tendencia. Así, quiero encontrar una tasa de cambio en un periodo de 12 meses para eliminar la variación estacional. Para encontrar la tendencia más reciente utilizo los datos más recientes con un periodo de tiempo de 12 meses.

\ begin {align*}\ text {Tasa de Cambio Mensual}\ amp =\ frac {Ventas (25) -Ventas (13)} {25-13}\\\ amp =\ frac {1298-1176} {25-13} =\ frac {122} {12}\ approx 10\ text {.} \ end {alinear*}

Vale la pena señalar que la necesidad de ajustar por el período de tiempo adecuado para las comparaciones es probablemente la razón por la que los informes de ingresos de las empresas suelen mostrar el trimestre anterior así como el trimestre de un año antes.

Un truco de Excel para cocientes de diferencia.

Figura$3.1.9.$ Video presentación de este tema

Al crear funciones marginales u otros cocientes de diferencia, a menudo queremos que los cálculos se mantengan en una fila, particularmente si queremos graficar la función y la función marginal juntas. Una cuidadosa disposición de las columnas y el uso de relleno rápido nos facilitarán la vida.

Supongamos que mi función de ingresos es$rev(q)=-0.2q^2+20q-5$ y quiero computar ingresos marginales. Entonces$rev(q+1)=-0.2(q+1)^2+20(q+1)-5\text{.}$ Experiencia demuestra que los estudiantes suelen cometer un error de mecanografía en la segunda fórmula, a menudo olvidando paréntesis en algún lugar de olvidarse de cambiar una de las copias de$q$ a$q+1\text{.}$

$clipboard_e7b1433fb04e10acbf4c482b1a1f5de99.png$

Una solución es agregar una columna extra para$q+1$ junto a la columna para$q\text{.}$ Luego la fórmula para$rev(q+1)$ se obtiene por llenado rápido formar la fórmula para$rev(q)\text{.}$

$clipboard_e43f443b47e18e2a2b9a2be45fb49e28e.png$

Este truco será aún más útil en la siguiente sección cuando queramos calcular los valores de$rev(q)\text{,}$$rev(q+0.00)\text{,}$ y$rev(q-0.001)\text{.}$

clase=”

Ejercicios Ejercicios: Funciones Marginales y Problemas de Cocientes de Diferencia

Ejercicio 1:

Si$\revenue(q)=5q\text{,}$ ¿cuál es el ingreso marginal por vender el décimo artículo?

Contestar

El ingreso marginal estaría dado por

\ begin {align*}\ Mrev (10)\ amp =\ revenue (10) -\ revenue (9)\\\ amp =50-45=5\ text {.} \ end {alinear*}

El ingreso marginal por vender el décimo artículo es de $5.

Ejercicio 2:

Si$\profit(q)=-100+5q-0.01q^2\text{,}$ ¿cuál es el beneficio marginal de vender el artículo 20?

Ejercicio 3:

Si$\cost(q)=100+7q\text{,}$ ¿cuál es el costo marginal de vender el artículo 30?

Contestar

El costo marginal estaría dado por

\ begin {align*}\ Mcosto (30)\ amp =\ costo (30) -\ costo (29)\\\ amp =2200-2193=7\ end {align*}

El costo marginal de vender el artículo 30 es de $7.

Ejercicio 4:

Si$\revenue(q)=-500+7q-0.01\sqrt{q^3}\text{,}$ ¿cuál es el ingreso marginal por vender el artículo número 100?

Ejercicio 5:

Si$\cost(q)$ es una función constante ¿qué se puede decir sobre la función de costo marginal? (Use álgebra para encontrar una fórmula para la función marginal.)

Insinuación.

$\Mcost(q+1)=\cost(q+1)-\cost(q)$

Contestar: $\Mcost(q+1)=\cost(q+1)-\cost(q)\text{,}$pero la función de costo es igual a alguna constante, por lo que$cost(q+1)=cost(q)\text{.}$ Esto implica que la función Costo Marginal debe ser 0.

Ejercicio 6:

Si$\revenue(q)$ es una función lineal con pendiente$m\text{,}$ ¿qué se puede decir de la función de ingresos marginales? (Use álgebra para encontrar una fórmula para la función marginal.)

Para el ejercicio$3.1.7–3.1.12$:

Hacer un gráfico de la función y la función marginal como q va de 0 a 30.
Trazar la función y la función marginal en la misma gráfica.
A partir de la forma de la gráfica de la función marginal, decidir qué tipo de gráfica parece ser.
Encuentre la fórmula para una curva de mejor ajuste para la función marginal.
Enumere las regiones donde la función original está aumentando y las regiones donde está disminuyendo.
Enumere las regiones donde la función marginal es positiva y donde la función marginal es negativa.

Ejercicio 7:

Let$\cost(q)=5000+23 q\text{.}$

Contestar

Recordemos que$\Mcost(q+1)=\cost(q+1)-\cost(q)\text{.}$
Las entradas en las celdas deben ser

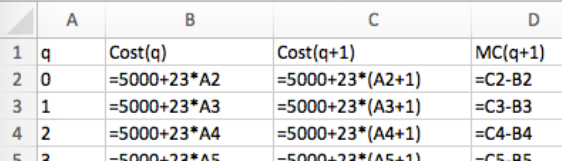
$clipboard_e527d26ccf103ac9c15e588395a0da1fd.png$

(Ver parte b para algunos de los valores)

Search

Definición\(3.1.1.\): Marginal value.

Ejemplo 3.1.2: Funciones Marginales para Widgets.

Ejemplo 3.1.3: Ganancia y Beneficio Marginal Juntos.

Ejemplo 3.1.5: Beneficio Marginal de Datos.

Ejemplo 3.1.7: Tasa de cambio cuando el denominador no es 1.

Ejercicio 1:

Ejercicio 2:

Ejercicio 3:

Ejercicio 4:

Ejercicio 5:

Ejercicio 6:

Ejercicio 7: