3.2: Derivadas numéricas y límites
- Page ID
- 116016
En la sección anterior, observamos las funciones marginales, la diferencia entre\(f(x+1)\) y\(f(x)\text{.}\) Para las funciones que solo se definen en valores enteros, esta es la forma obvia de definir una tasa de cambio. Sin embargo, para las funciones que se definen en un intervalo, nos gustaría usar la información en valores más cercanos a nuestro valor de\(x\text{.}\)
Intuitivamente, nos gustaría poder acercar la gráfica de\(f(x)\) en un punto hasta que la gráfica se vea como una línea recta, luego elegir dos puntos en esa línea, y encontrar la pendiente como la subida sobre la carrera. La tasa de cambio es entonces la pendiente de la línea que hemos encontrado. Si pudiéramos hacer zoom arbitrariamente lejos, este proceso daría una tasa instantánea de cambio, o la derivada de la función en ese punto.
Para una función,\(f(x)\text{,}\) la tasa instantánea de cambio de\(f(x)\) at\(x=x_0\text{,}\) o la derivada de\(f(x)\text{,}\) at\(x=x_0\text{,}\) denotada como\(f'(x)\text{,}\) se define como
\[ f'(x_0 )=\lim_{(\Delta x\to 0)}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\text{,} \nonumber \]
donde\(\lim_{ x\to a}f(x)\) se entiende como valor que\(f(x)\) se acerca arbitrariamente al hacer\(x\) arbitrariamente cercano a\(a\text{.}\)
El símbolo\(\Delta\) es la letra griega captial Delta, que se usa comúnmente para significar un cambio en las ciencias. Como no podemos ingresar fácilmente letras griegas en una hoja de cálculo de Excel, usaremos del x para representar\(\Delta x\) en Excel.
Nuestra tarea en esta sección es convertir nuestra noción y definición intuitivas y en un proceso que nos permita encontrar el valor, y encontrarlo de manera eficiente.
Vamos\(f(x)=x^2\text{.}\) Nos gustaría encontrar\(f'(1)\text{.}\)
Figura\(3.2.3.\) Video presentación de este ejemplo
Solución
Solución. 1 Solución A
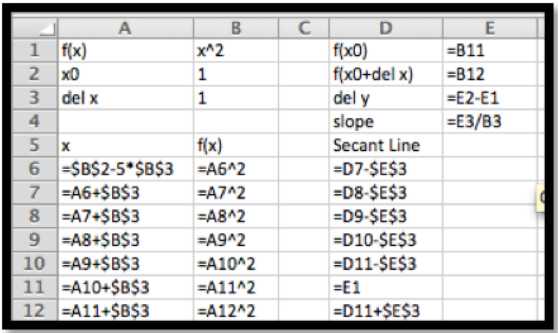
Comenzamos con nuestra noción intuitiva. Queremos mirar la gráfica de\(f(x)\text{,}\) zoom lo suficiente como para que la gráfica se vea como una línea recta. Yo configuro una hoja de trabajo para mirar la gráfica de\((x)=x^2\) cerca\(x_0=1\text{.}\) Ya que quiero poder acercar, configuro la gráfica para que se traze puntos que son múltiplos de\(\Delta x\) desde también\(x=x_0\text{.}\) quiero trazar la línea que conecta los puntos\((x_0,f(x_0))\) y\((x_0,f(x_0+\Delta x))\) y noto que la pendiente de la línea secante entre ellos es
\[ \frac{f(x_0+\Delta x)-f(x_0 )}{\Delta x}\text{.} \nonumber \]
Para este ejemplo\(x_0=1\text{.}\) Si\(\Delta x=1\text{,}\) podemos ver que la función y la línea secante son claramente distintas.

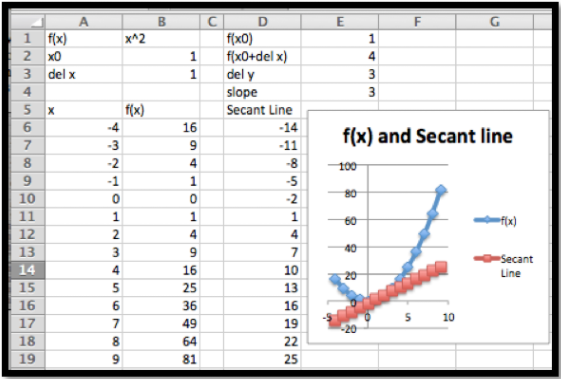
La hoja de trabajo está diseñada para facilitar el cambio del valor de\(\Delta x\text{.}\)

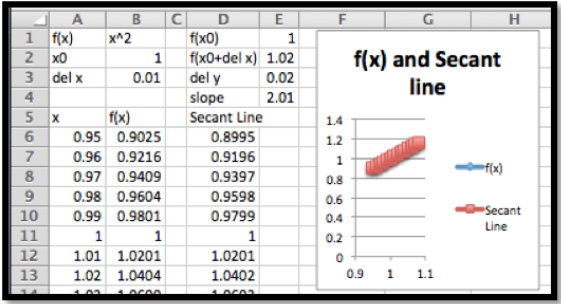
Como podemos ver, si dejamos que\(\Delta x=1\text{,}\) la pendiente sea 3, pero no hemos acercado lo suficiente para que la gráfica de\(f(x)\) se vea como una línea recta. Dejar que\(\Delta x=0.01\text{,}\) la pendiente sea de 2.01, y las gráficas de la función y la línea secante parecen ser las mismas.

Con cierta experimentación, tomando valores tanto positivos como negativos de\(\Delta x\text{,}\) obtenemos la siguiente tabla de valores:
| \(\Delta x\) | pendiente | \(\ \ \ \) | \(\Delta x\) | pendiente |
| 1 | 3 | \(\ \ \ \) | -1 | 1 |
| 0.1 | 2.1 | \(\ \ \ \) | -0.1 | 1.9 |
| 0.01 | 2.01 | \(\ \ \ \) | -0.01 | 1.99 |
| 0.001 | 2.001 | \(\ \ \ \) | -0.001 | 1.999 |
Está claro que a medida que\(\Delta x\) se hace muy pequeña, la pendiente de la línea tangente se acerca cada vez más a 2. Así\(f'(1)=2\text{.}\)
El método de la primera solución requiere demasiado trabajo y requiere que restablecemos una hoja de trabajo y hagamos un seguimiento de la pendiente mientras intentamos una serie de valores para\(\Delta x\text{.}\) Nos gustaría crear una hoja de trabajo que simplemente muestre los valores de la pendiente de la línea secante para valores de\(\Delta x\) y tome el valor que esto se acerca. Podemos configurar una hoja de trabajo donde cada línea toma\(\Delta x\) de la línea anterior y se divide por 10.

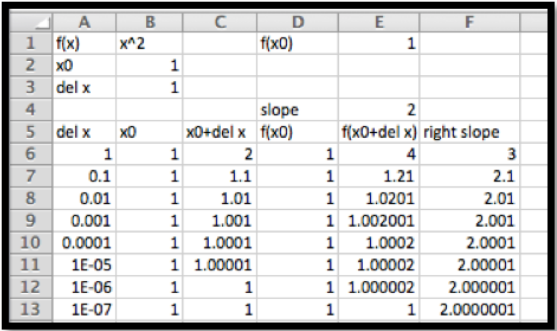
Obtenemos el mismo valor ya sea que empecemos\(\Delta x\) en 1 o -1. Una vez más, encontramos\(f'(1)=2\text{.}\)
Este método de encontrar la derivada todavía tiene una serie de dificultades. En el ejemplo anterior, la respuesta exacta que queremos (en este caso 2) no se presentó en ninguno de nuestros cálculos. También encontramos que si hacemos\(\Delta x\) demasiado pequeños, nos encontramos con un problema llamado error de redondeo. Si el siguiente capítulo veremos métodos que computan simbólicamente derivados, pero para este capítulo queremos un método fácil de aproximación. Utilizaremos la técnica de aproximación que utilizan la mayoría de las calculadoras gráficas cuando computan la derivada. Utilizan un “cociente de diferencia equilibrada” donde encontramos la pendiente de la línea secante entre los puntos\(\Delta x\) antes y después del punto que nos interesa. Como muestra la siguiente imagen, en comparación con la secante derecha o la secante izquierda, para la mayoría de las funciones la secante equilibrada está más cerca de ser paralela a la línea tangente.

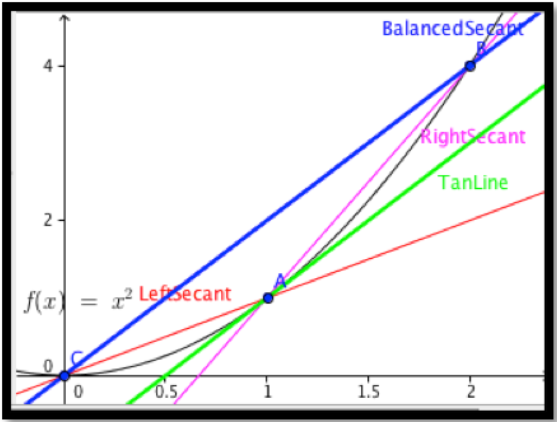
Usaremos el valor por defecto en las calculadoras, es decir usaremos\(\Delta x = 0.001\text{.}\)

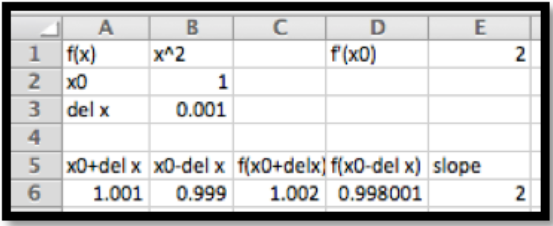
Para nuestro ejemplo esto da nuestro resultado familiar que\(f'(1)=2\text{.}\)
Formalizamos este último acercamiento.
\[ f'(x)\approx\frac{f(x+.001)-f(x-0.001)}{.002}\text{.} \nonumber \]
Para el resto de este texto, cuando necesitamos calcular una aproximación numérica a la derivada utilizaremos la aproximación calculadora de la derivada.
Debemos señalar que la regla de la calculadora es una técnica de aproximación, más que una definición. Dará una respuesta engañosa para funciones que no se aproximen a una línea recta en una ventana de 0.002 de ancho. En este curso, la aproximación solo provocará un problema con funciones que tengan esquinas o cúspides, como las funciones\(f(x)=|x|\) y\(f(x)=x^{(2/3)}\) en\(x=0\text{.}\) La principal ventaja de usar la regla de la calculadora es que es lo suficientemente sencilla como para computar para permitirnos trazar una función y su derivada en una sola gráfica. Esto nos permite comparar la gráfica de la función con la gráfica de la derivada.
Figura Presentación en\(3.2.5.\) video de los siguientes dos ejemplos
Compare la gráfica de\(f(x)=x^2-2 x+1\) y la gráfica de su derivada, utilizando ejes separados para las dos gráficas. Qué características de la gráfica se\(f(x)\) pueden ubicar usando la gráfica de\(f'(x)\text{?}\)
Solución
Dado que este problema nos servirá como plantilla para una pregunta la veremos muchas veces, vale la pena mirarla a detalle. Comenzamos configurando un libro de trabajo que tendrá la estructura que necesitamos para calcular un gráfico de valores\(f(x)\) y\(f'(x)\text{.}\)

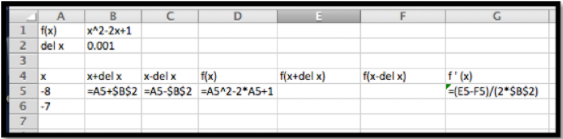
La imagen de arriba da la cantidad mínima que necesitamos para escribir. El resto se hará con llenado rápido. La entrada de la celda B1 da la fórmula para la función. En la celda D5 evaluamos la función utilizando el primer valor de\(x\) desde la celda A5. Tenemos dos valores de\(x\) en las celdas A5 y A6 para que podamos rellenar rápidamente para obtener una lista de\(x\) valores. Utilizamos referencias absolutas para\(\Delta x\text{,}\) lo que no cambiará en los rellenos rápidos. Luego llenamos las celdas E5 y F5 de la celda D5, luego llenamos la fila 6 de la fila 5, luego llenamos el resto del gráfico a partir de las filas 5 y 6.

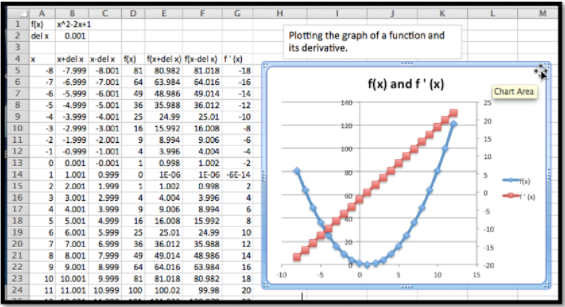
Entonces es una tarea sencilla trazar las dos curvas. Notamos que la gráfica de la función es una parábola. Si la derivada es negativa, la gráfica de\(f(x)\) es decreciente. Si la derivada es positiva, la gráfica de la función\(f(x)\) va en aumento. El gráfico de\(f(x)\) alcanza su mínimo en el vértice, que es también donde también\(f'(x)=0\text{.}\) notamos que la derivada de esta parábola parece ser una línea recta.
Varias de nuestras observaciones de este ejemplo funcionan en general. Mirando un solo punto, la derivada de una función es la pendiente de la línea tangente a la gráfica en ese punto. La línea tangente es una mejor aproximación lineal a la gráfica en un punto. Al observar la derivada en muchos puntos, la gráfica de una función aumenta cuando la derivada es positiva, y la gráfica de una función disminuye cuando la derivada es negativa. Para que la gráfica tenga un punto que sea localmente máximo o mínimo, la derivada no puede ser positiva ni negativa, por lo que la derivada debe ser cero o indefinida para que la gráfica de la función tenga un máximo o mínimo. Encontrar lugares donde las funciones alcancen sus valores más altos y más bajos es una actividad importante en matemáticas. Analizaremos estas aplicaciones con más profundidad en las próximas secciones. Se advierte al lector que podemos tener lugares donde la derivada es cero pero la función sigue aumentando o disminuyendo.
Compare la gráfica de\(f(x)=x^3 (x^2-36)\) y la gráfica de su derivada, utilizando ejes separados para las dos gráficas. Qué características de la gráfica se\(f(x)\) pueden ubicar usando la gráfica de\(f'(x)\text{?}\)
Solución
La configuración para este ejemplo es muy similar al último problema.

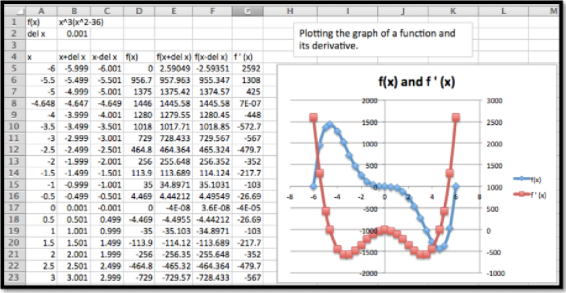
Esta vez notamos tres lugares donde la derivada parece ser cero, cuando\(x\) está cerca\(-5\text{,}\)\(0\text{,}\) y\(5\text{.}\) usamos goal seek en la derivada y encontramos que la derivada es cero cuando\(x=-4.648\text{,}\) 0, o 4.648. Al mirar la gráfica de f (x) en esos puntos, vemos que\(f(x)\) tiene un máximo cuando\(x=-4.648\text{,}\) y un mínimo cuando\(x=-4.648\text{.}\) Cuando no\(x=0\text{,}\)\(f(x)\) es ni un máximo ni un mínimo.
En el siguiente capítulo veremos formas de encontrar simbólicamente la derivada de una función. Ya podemos razonar nuestra manera de encontrar simbólicamente la derivada de funciones simples. Si nuestra función\(f(x)\) es constante o lineal, entonces la gráfica de la función es su propia línea tangente, por lo que la derivada es simplemente la pendiente de la gráfica. Para las funciones cuadráticas notamos que la gráfica de la derivada parece ser lineal. Si podemos adivinar la forma del derivado, podemos usar líneas de tendencia para producir una fórmula.
Figura\(3.2.9\). Video presentación de este ejemplo
Use líneas de tendencia para encontrar una fórmula para la derivada de\(f(x)=2x^2+5x-7\text{.}\)
Solución
La configuración para este ejemplo es muy similar al último problema. Simplemente cambiamos la función. Esto implica cambiar las fórmulas en las celdas B1 y D5, luego usar copia rápida para cambiar las fórmulas de las celdas en las columnas D a F.

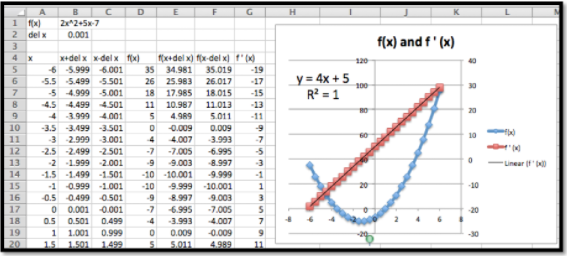
Una vez que tenemos puntos para la derivada agregamos una línea de tendencia usando un modelo lineal. Establecemos las opciones para mostrar tanto la fórmula para la línea de tendencia como el valor de\(R^2\text{.}\) El hecho que\(R^2=1\text{,}\) indica la línea de tendencia que encontramos se ajusta exactamente a los datos. En el libro de trabajo conectado a esta sección hay una página para el Ejemplo 6B. Utiliza parámetros para los coeficientes en una fórmula cuadrática, para que puedas explorar la derivada de una función cuadrática general.
Una Nota sobre Terminología.
Vale la pena señalar cierta ambigüedad en los términos utilizados en esta sección y en la sección anterior. Hemos estado usando el término\(\marginal f(x+1)\) para el cambio\(f(x+1)-f(x)\text{,}\) donde\(f(x)\text{,}\) podría ser ingresos, o costo, o ganancia. Esta es la definición estándar de una función marginal desde las finanzas o la economía. Sin embargo, si haces una búsqueda en la web sobre “ingresos marginales de cálculo” encontrarás que la mayoría de los libros de cálculo tratan la función marginal como simplemente otro nombre para la derivada. Si bien están relacionados, no son lo mismo. En el siguiente capítulo encontraremos que a menudo es más fácil producir una fórmula para la derivada de una función en lugar de la función marginal relacionada, razón por la cual la derivada se usa para la función marginal. No obstante, en este texto, nos apegaremos a la correcta definición de funciones marginales.
Resumen.
La noción de derivada es uno de los conceptos clave del cálculo. El concepto de la derivada de una función está estrechamente relacionado con el concepto de función marginal. Damos tres formas de entender la derivada de una función en un punto.
- Comprensión intuitiva
-
La derivada de\(f(x)\text{,}\) at\(x=x_0\) denotada como\(f'(x_0)\text{,}\) es la pendiente de la línea obtenida al hacer zoom en la gráfica\((x_0,f(x_0 ))\) hasta que se vea como una línea recta.
- Definición formal
-
La derivada de\(f(x)\text{,}\) denotada como\(f'(x)\text{,}\) se define como
\[ f'(x)=\lim_{\Delta x\to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\text{.} \nonumber \]
- La aproximación de la calculadora
-
El derivado de\(f(x)\text{,}\) puede aproximarse usando la fórmula
\[ f'(x)\approx \frac{f(x+.001)-f(x-0.001)}{.002}\text{.} \nonumber \]
Ejercicios: Derivadas numéricas y límites
- Para cada función y valor x especificados, haga lo siguiente:
- Encuentre un valor lo suficientemente\(\Delta x\) pequeño como para que el gráfico de la función parezca una línea recta en la región desde\(5*\Delta x\) antes del valor x hasta\(5*\Delta x\) después del valor x. Grafica la función en esta región y encuentra la pendiente de la línea secante correspondiente
- Estimar la derivada encontrando la pendiente de la secante cuando\(\Delta x\) toma los valores 0.1, 0.01, 0.001, 0.0001, -0.1, -0.01, -0.001 y -0.0001. Dar un valor del límite de la pendiente.
- Utilice la estimación de la calculadora para estimar la pendiente de la tangente.
- Comparar el valor de la derivada\(f'(x)\) con el valor correspondiente de la función marginal\(marginal\ f(x+1)\text{.}\)
Comentario: Para los problemas 1-10 tiene sentido configurar la tabla una vez con parámetros que se puedan cambiar fácilmente entre problemas.
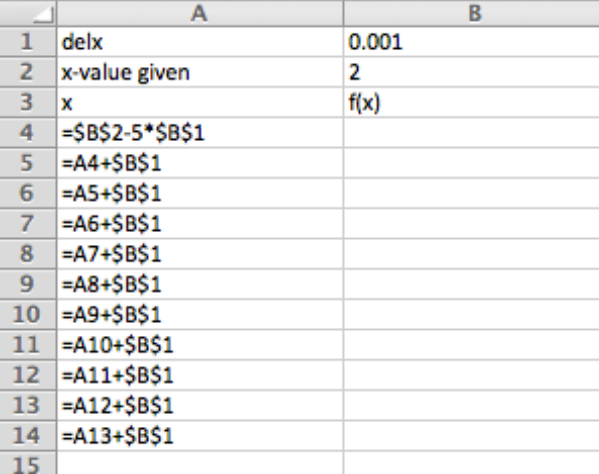
Comandos de Excel
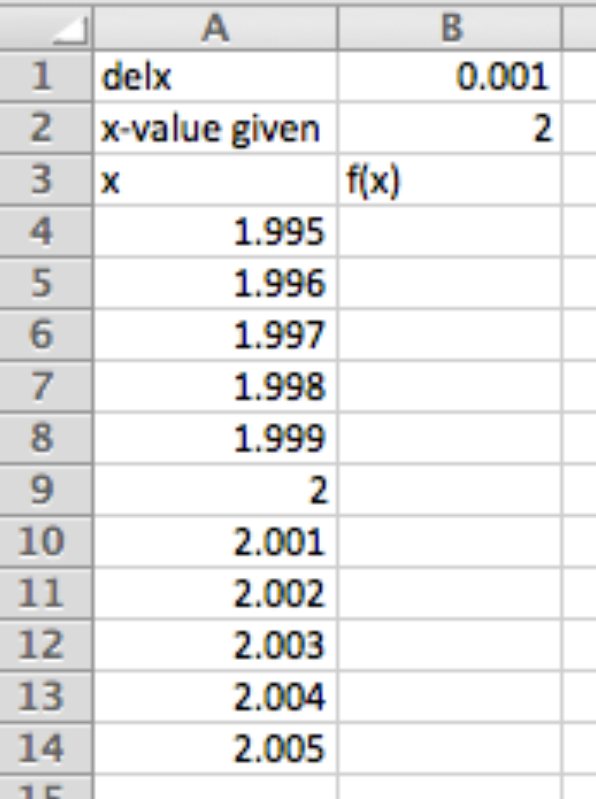
Salida de Excel
Cambiar\(\Delta x\) (delx) y\(x\) -valor dado dependiendo del problema, y ajustar la función y el resto se autocompletará. Una vez que se haya agregado la gráfica se actualizará también.
Uso\(f(x)=x^2+3\) en\(x=2\text{.}\)
- Contestar
-
- Usando
Slope= (B14-B4)/(10*B1)obtenemos lo siguiente
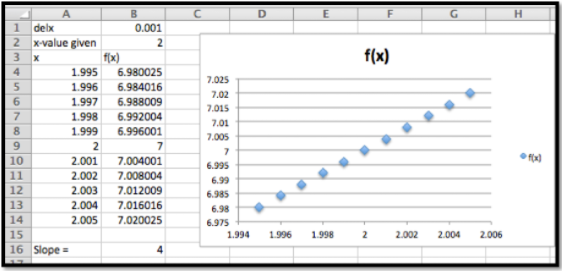
- Usando
Por lo que la pendiente para esta elección de delx es 4.
Es posible que haya elegido un poco diferente\(\Delta x\text{,}\) y siempre y cuando el gráfico se vea más o menos lineal, estaría bien.


