5.1: Diferenciación implícita

A menudo nos encontramos con situaciones en las que y no se expresa en función de x, sino como en relación con x El ejemplo más familiar es la ecuación para un círculo de radio 5

\[ x^2+y^2=25. \nonumber \]

Recordamos que un círculo no es en realidad la gráfica de una función. Sin embargo, es el gráfico combinado de las dos funciones que representan las mitades superior e inferior del círculo.

Tenemos dos enfoques si queremos encontrar la pendiente de la línea tangente al círculo en Primero\((4,3)\text{.}\) podríamos usar álgebra para expresar\(y\) en función de\(x\text{,}\) y luego usar nuestras reglas para encontrar la derivada. Ese enfoque funciona en este problema pero fallará con relaciones más complicadas. El método alternativo es decir que\(y\) es implícitamente una función de\(x\text{.}\) Podemos entonces usar la regla de la cadena para tomar la derivada de la relación con la derivada de\(y\) ser designada como\(y'\text{.}\) Podemos entonces resolver para\(y'\) en términos de\(x\) y\(y\text{.}\) Este segundo se llama diferenciación implícita.

Comenzamos probando ambos enfoques sobre la ecuación de un círculo.

Ejemplo 5.1.1: Tangente a un círculo

Encuentra la ecuación de la línea tangente a\(x^2+y^2=25\) at\((4,3)\text{.}\)

Solución

R: Para encontrar la ecuación de una línea necesitamos un punto y una pendiente. Ya tenemos el punto en\((4,3)\text{.}\) Para encontrar la pendiente, podemos expresar el círculo como la gráfica de 2 funciones. Primero resolvemos para Luego\(y^2\text{.}\) tomamos la raíz cuadrada para producir 2 funciones.

\[ y^2=25-x^2. \nonumber \]

\[ f_1 (x)=\sqrt{25-x^2 }. \nonumber \]

\[ f_2 (x)=-\sqrt{25-x^2 }. \nonumber \]

El punto está en la primera función, que es la mitad superior del círculo, así que tomamos su derivada y evaluamos en\(x=4\text{.}\)

\[ f_1' (x)=1/2 (25-x^2 )^{-1/2} (-2x). \nonumber \]

\[ f_1' (4)=1/2 (25-4^2 )^{-1/2} (-4)=-4/3. \nonumber \]

Así, la línea tangente, en forma de punto-pendiente, es:

\[ y=3-\frac{4}{3} (x-4). \nonumber \]

B: Para encontrar la ecuación de una línea necesitamos un punto y una pendiente. Ya tenemos el punto en\((4,3)\text{.}\) Para encontrar la pendiente tomamos la derivada de nuestra ecuación. Ya que no tenemos y en función de simplemente\(x\text{,}\) notamos que su derivada es el marcador de posición\(y'\text{.}\) Recordemos que\(\frac{d}{dx} x\text{,}\) la derivada de\(x\) con respecto a\(x\text{,}\) es simplemente 1.

\[ \frac{d}{dx}(x^2+y^2=25). \nonumber \]

\[ \frac{d}{dx}(x^2)+\frac{d}{dx}(y^2)=\frac{d}{dx}(25). \nonumber \]

\[ 2x \frac{d}{dx}(x)+2y \frac{d}{dx}(y)=0. \nonumber \]

\[ 2x+2y y'=0. \nonumber \]

Luego resolvemos\(y'\) y sustituimos nuestro punto\((4,3)\) por\((x,y)\text{.}\)

\[ y'=-\frac{2}{2y}=-\frac{x}{y}. \nonumber \]

Cuando sustituimos nuestro punto\((4,3)\) por\((x,y)\) obtenemos el mismo valor,\(y'=-\frac{4}{3}\text{.}\) así la línea tangente, en forma de punto-pendiente, es:

\[ y=3-\frac{4}{3} (x-4). \nonumber \]

Para la ecuación de un círculo, cualquiera de los dos métodos funciona. Podemos encontrar relaciones donde resolver una función explícita es difícil o imposible.

Ejemplo 5.1.2: Diferenciación de una Relación Precio-Cantidad.

La cantidad (q) y el precio de demanda (p) para widgets satisfacen la relación

\[ 10p+2pq+q^2=1000, \nonumber \]

con\(10\lt q\lt 90\text{,}\) donde la cantidad es en miles de unidades. Si actualmente estoy vendiendo 20,000 widgets, ¿cuál es la relación entre el cambio de cantidad y el cambio de precio?

Solución

En lugar de resolver por cantidad como una función explícita del precio, vamos a diferenciar implícitamente.

\[ \frac{d}{d\ q}(10p+2pq+q^2=1000) \nonumber \]

\[ 10 \frac{d\ p}{d\ q}+2*\frac{d\ p}{d\ q}*q+2p+2q=0 \nonumber \]

\[ \frac{d\ p}{d\ q} (10+2q)=-2*(p+q) \nonumber \]

\[ \frac{d\ p}{d\ q}=\frac{-2*(p+q)}{(10+2q) } \nonumber \]

Ya que la cantidad está en miles de unidades, si estamos vendiendo 20,000 widgets,\(quantity:q=20\) y\(price:p=14.64\text{.}\) Sustituyendo esos valores en la fórmula por la derivada de precio con respecto a la cantidad, vemos

\[ \frac{d\ price}{d\ quantity}=\frac{-2(14.64+20)}{(10+2*20) }=-1.386. \nonumber \]

Aumentamos las ventas en 1000 al bajar el precio en $1.386.

Para los dos primeros ejemplos, la relación era cuadrática, por lo que fue sencillo encontrar la derivada ya sea resolviendo para una función explícita o diferenciando implícitamente. Sin embargo, si la relación es más complicada encontraremos la diferenciación implícita más fácil que resolver para la función.

Ejemplo 5.1.3:

La cantidad (q) y el precio de demanda (p) para artilugios satisfacen la relación

\[ 5p+3*(pq)^{1.5}+2q=2000, \nonumber \]

con\(10\lt q\lt 100\text{,}\) donde la cantidad es en miles de unidades. Si actualmente estoy vendiendo 25,000 widgets, ¿cuál es la relación entre el cambio de cantidad y el cambio de precio?

Solución

No existe un método fácil para resolver esta relación ni por precio ni por cantidad como una función explícita del otro. En cambio, vamos a diferenciar implícitamente.

\[ \frac{d\ }{d\ q}(5*p+3*(p*q)^1.5+2*q=2000) \nonumber \]

\[ 5 \frac{d\ p}{d\ q}+3*(1.5*p^.5*(d p)/(d q)*q^{1.5}+p^{1.5}*1.5*q^{.5} )+2=0 \nonumber \]

\[ \frac{d\ p}{d\ q}*(5+4.5*p^{.5}*q^{1.5} )=-(2+4.5*p^{1.5}*q^{.5}) \nonumber \]

\[ \frac{d\ p}{d\ q}=-\frac{(2+4.5*p^{1.5}*q^{.5})}{(5+4.5*p^{.5}*q^{1.5} ) } \nonumber \]

Ya que la cantidad está en miles de unidades, si estamos vendiendo 25,000 widgets, quantity=25 y price=2.986. Sustituyendo esos valores en la fórmula para el derivado del precio con respecto a la cantidad, vemos

\[ \frac{d\ price}{d\ quantity}=\frac{-118.104}{997.025}=-0.12088. \nonumber \]

Aumentamos las ventas en 1000 al bajar el precio en 0.121 dólares.

Un resultado estándar de la economía es la ecuación Cobb-Douglas que afirma

\[ Y=AL^\alpha K^\beta, \nonumber \]

donde Y, L y K representan la producción total, la mano de obra y el capital, respectivamente. En el modelo clásico\(\alpha+\beta=1\text{.}\)

Esto puede entenderse como una relación que involucra capital y trabajo. Una pregunta interesante es preguntar por la tasa de cambio de capital con respecto a la mano de obra, o cómo aumentar o reducir la inversión de capital elevará o bajará los costos laborales.

Ejemplo 5.1.4: Diferenciación de Cobb-Douglas.

Ejemplo 4: Un fabricante de widgets tiene una función de producción dada por

\[ Y=50L^.75 K^.25. \nonumber \]

Actualmente el fabricante utiliza 81 unidades de mano de obra y 16 unidades de capital. Encuentra la derivada del trabajo con respecto al capital e interpreta tu resultado.

Solución

Diferenciamos implícitamente nuestra ecuación con respecto al capital.

\[ \frac{d\ }{d\ K}(Y=50L^{.75} K^{.25}) \nonumber \]

\[ 0=50*(0.75*L^{-0.25}*\frac{d\ L}{d\ K}*K^{.25}+L^{.75}*.25*K^{-0.75} ) \nonumber \]

\[ \frac{d\ L}{d\ K}*(0.75*L^{-0.25}*K^{.25} )=-(L^{.75}*.25*K^{-0.75}) \nonumber \]

\[ \frac{d\ L}{d\ K}*=-(L^{.75}*.25*K^{-0.75})/((0.75*L^{-0.25}*K^{.25} ) )=-L/3K \nonumber \]

Sustituyendo en nuestros valores por\(L\) y K vemos eso\(Y=50*81^{.75} 16^{.25}=2700\) y\((d L)/(d K)=-81/48\approx-1.6875\text{.}\) Esto significa que, si queremos mantener nivel de producción, cambiar la inversión de capital por 1 unidad nos permite cambiar la mano de obra en -1.6875 unidades.

Diferenciación implícita usando CAS

Al igual que con la diferenciación regular, podemos usar sistemas de álgebra computacional en línea para hacer diferenciación implícita. La forma más fácil de hacerlo es con una búsqueda web de calculadora de diferenciación implícita.

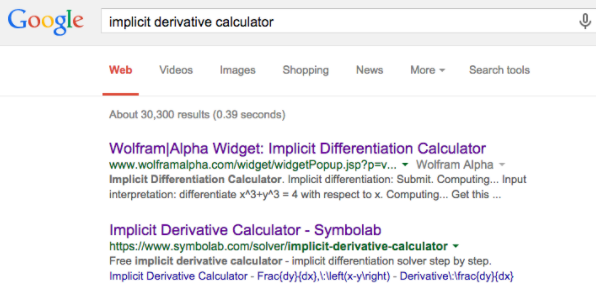
La primera opción que se nos da es una interfaz de widget para WolframAlpha. Fácilmente nos permite hacer el primer ejemplo en esta sección.

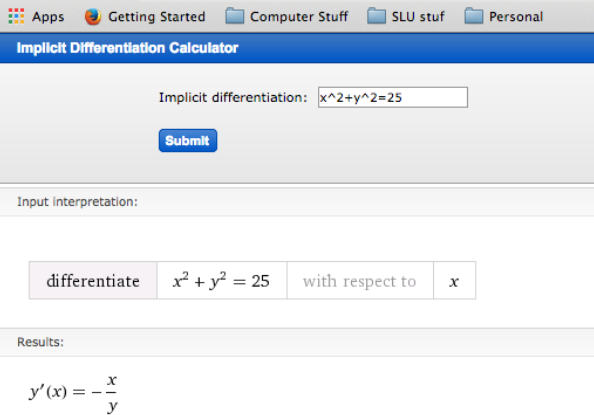
La segunda opción de la búsqueda nos lleva a una calculadora de Symbolab. Fácilmente hará el segundo ejemplo de esta sección.

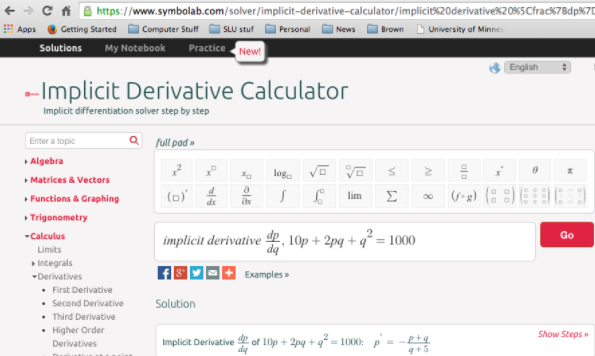
Debe notar que la calculadora Symbolab le permite usar otras variables y tiene una opción fácil para mostrar soluciones paso a paso.

Resumen

La diferenciación implícita es una aplicación de la regla de la cadena. Para utilizar esta técnica necesitamos una ecuación entre dos variables que podamos pensar que definen implícitamente una variable en función de la otra. Si suponemos que una variable es implícitamente una función de la otra, diferenciar la ecuación nos da una ecuación en las dos variables y la derivada. Entonces podemos usar álgebra para resolver la nueva ecuación para la derivada.

clase=”

Ejercicios: Problemas de diferenciación implícita

Para las siguientes ecuaciones encuentra la derivada especificada.

Ejercicio 1:

\(2x+3y=23\text{.}\)Encuentra\(\frac{dy}{dx}\text{.}\)

Responder

El mejor método es notar que esta es una línea con pendiente\(\frac{-2}{3}\text{.}\) Sumergirse adelante sin darse cuenta de que:

\[ \frac{d}{dx} (2x+3y )= \frac{d}{dx} 23 \nonumber \]

\[ \text{Implies that }2+ \frac{dy}{dx} =0 \nonumber \]

Resolver para\(\frac{dy}{dx}\text{:}\)

\[ \frac{dy}{dx} =\frac{-2}{3} \nonumber \]

Ejercicio 2:

\(7x+9y=23\text{.}\)Buscar\(\frac{dy}{dx}\text{.}\) (Puedes usar dos métodos diferentes.)

Ejercicio 3:

\(x^2+3xy+5y^2=23\text{.}\)Encuentra\(\frac{dy}{dx}\text{.}\)

Responder

\[ \frac{d}{dx} (x^2+3xy+5y^2 )= \frac{d}{dx} 23 \nonumber \]

\[ \text{Implies that }2x+3 \frac{d}{dx} (xy)+5 \frac{d}{dx} y^2=0 \nonumber \]

Para el\(\frac{d}{dx} (xy)\) término necesitamos usar la regla del producto y para\(\frac{d}{dx} y^2\) necesitamos la regla de la cadena. Entonces conseguimos

\[ 2x+3[(1)y+x\frac{dy}{dx}]+5 (2y)\frac{dy}{dx} =0 \nonumber \]

Resolver para\(\frac{dy}{dx}\text{:}\)

\[ 2x+3y+3x \frac{dy}{dx}+10y \frac{dy}{dx} =0 \nonumber \]

\[ \text{Hence }(3x+10y) \frac{dy}{dx} =-(2x+3y) \nonumber \]

\[ \text{And }\frac{dy}{dx} =-((2x+3y))/((3x+10y) ) \nonumber \]

Ejercicio 4:

\((x^3+x^2+1)(y^3+2y+3)=5\text{.}\)Encuentra\(\frac{dy}{dx}\text{.}\)

Ejercicio 5:

\(75*price+(quantity^2)/100=2000\text{.}\)Encuentra\(\left(\frac{d\ price}{d\ quantity}\right)\text{.}\)

Responder

Algunos pueden encontrar esto más fácil con etiquetas variables más cortas:\(75P+Q^2/100=2000\text{.}\) Buscar\(\frac{dP}{dQ}\text{.}\)

\[ \frac{d}{dQ} [75P+\frac{Q^2}{100}]=\frac{d}{dQ} 2000 \nonumber \]

\[ 75 \frac{dP}{dQ}+\frac{Q}{50}=0 \nonumber \]

De ahí\(\frac{dP}{dQ}=- \frac{Q}{50*75}= \frac{-Q}{3750}\)

Así que tenemos eso\(\frac{dPrice}{dQuantity}/= \frac{-Quantity}{3750}\text{.}\)

Entonces, si aumentáramos la Cantidad en 1 (\(d\ Quantity = 1\)), entonces habría una disminución en price (\(= d Price\)) igual a la Cantidad dividida por 3750. Por lo que un pequeño aumento en la cantidad resultaría en una (pequeña) disminución del precio.

Ejercicio 6:

\(50*price+5*price*quantity+(quantity^2)/10=5000\text{.}\)Encuentra\(\frac{d\ price}{d\ quantity}\text{.}\)

Ejercicio 7:

\(40*price+7*price*quantity+\sqrt{quantity}=2000\text{.}\)Encuentra\(\frac{d\ price}{d\ quantity}\text{.}\) w

Responder

Reescribir como:\(40p+7pq+\sqrt{q}=2000\text{.}\) Buscar\(\frac{d\ p}{d\ q}\text{.}\)

Tomamos la derivada con respecto a q de ambos lados. En otras palabras, aplicamos\(\frac{d}{d\ q}\) a ambos lados.

\[ \frac{d}{d\ q} [40p+7pq+q^{0.5} ]=\frac{d}{d\ q} 2000 \nonumber \]

\[ 40 \frac{d\ p}{d\ q}+7[dp/dq q+p]+0.5 q^{-0.5}=0 \nonumber \]

\[ (40+7q)\frac{d\ p}{d\ q}+7p+0.5 q^{-0.5}=0 \nonumber \]

\[ \frac{d\ p}{d\ q}= \frac{-7p-0.5 q^{-0.5}}{40+7q} \nonumber \]

Ejercicio 8:

\(50*price^2+5*price*quantity=3000\text{.}\)Encuentra\(\frac{d\ price}{d\ quantity}\text{.}\)

Ejercicio 9:

\(1000=5L^{0.6} K^{0.4}\text{.}\)Encuentra\(\frac{dK}{dL}\text{.}\)

Responder

Tomar la derivada respecto\(L\) a ambos lados:

\[ \frac{d}{dL} 1000=5 \frac{d}{dL} [L^{0.6} K^{0.4} ] \nonumber \]

\[ 0=5[\frac{d}{dL}(L)^{0.6})K^{0.4}+L^{0.6} \frac{d}{dL}(K^{0.4})] \qquad \text{(product rule)} \nonumber \]

\[ 0=5[0.6 L^{-0.4} K^{0.4}+L^{0.6} 0.4K^{-0.6} \frac{dK}{dL}] \nonumber \]

Divide ambos lados por 5 y resuelve\(\frac{dK}{dL}\text{.}\)

\[ \frac{dK}{dL}=- \frac{0.6 L^{-0.4} K^{0.4}}{L^{0.6} 0.4K^{-0.6}}= \frac{-3K}{2L}. \nonumber \]

Ejercicio 10:

\(2000=7L^.3 K^.7.\)Encuentra\(\frac{dK}{dL}\text{.}\)

Ejercicio 11:

\(3000=2L^.25 K^.75\text{.}\)Encuentra\(\frac{dL}{dK}\text{.}\)

Responder

\[ \frac{d}{dK} 3000=2 \frac{d}{dK} [L^{0.25} K^{0.75} ] \nonumber \]

\[ 0=2[\frac{d}{dK}( L^{0.25}) K^{0.75}+L^{0.25} \frac{d}{dK}( K^{0.75} )] \qquad\text{(product rule)} \nonumber \]

\[ 0=2[0.25L^{-0.75}\frac{dL}{dK} K^{0.75}+L^{0.25} 0.75K^{-0.25} ] \nonumber \]

\[ \frac{dL}{dK}=-\frac{L^{0.25} 0.75K^{-0.25}}{0.25L^{-0.75} K^{0.75}} =-3 \frac{L}{K}. \nonumber \]

Ejercicio 12:

7\(000=11L^.8 K^.2\text{.}\) Buscar\(\frac{dL}{dK}\text{.}\)

Ejercicio 13:

La función de producción para una fábrica de widgets es\(1000=15L^{0.7} K^{0.3}\text{.}\) Buscar\(\frac{dK}{dL}\) e\(\frac{dL}{dK}\text{.}\) interpretar lo que significan.

Responder

Parte 1 Buscar\(\frac{dK}{dL}\)

\[ \frac{d}{dL} 1000=15\frac{d}{dL}[L^{0.7} K^{0.3}] \nonumber \]

\[ 0=15[\frac{d}{dL} (L^{0.7} )K^{0.3}+L^{0.7} \frac{d}{dL} (K^{0.3})] \nonumber \]

\[ 0=[0.7 L^{-0.3} K^{0.3}+L^{0.7} 0.3K^{-0.7} \frac{dK}{dL}] \nonumber \]

\[ \frac{dK}{dL}L=\frac{-0.7 L^{-0.3} K^{0.3}}{L^{0.7} 0.3K^{-0.7}} = -\frac{7K}{3L}. \nonumber \]

Parte 2 Buscar\(\frac{dL}{dK}\text{.}\)

\[ \frac{d}{dK} 1000=15\frac{d}{dK}[L^{0.7} K^{0.3}] \nonumber \]

\[ 0=15[\frac{d}{dK} (L^{0.7}) K^{0.3}+L^{0.7} \frac{d}{dK} (K^{0.3})] \nonumber \]

\[ 0=[0.7 L^{-0.3} \frac{dL}{dK} K^{0.3}+L^{0.7} 0.3K^{-0.7}] \nonumber \]

\[ \frac{dL}{dK}= \frac{- 0.3 L^{0.7} K^{-0.7}}{0.7 L^{-0.3} K^{0.3}} = \frac{-3L}{7K}. \nonumber \]

Parte 3 Interpretar

\(\frac{dK}{dL}\)y ambos\(\frac{dL}{dK}\) son negativos y son recíprocos el uno del otro. En otras palabras:\(\frac{dK}{dL}=\frac{1}{\frac{dL}{dK}}\text{.}\)

Ya que son negativos, si aumentamos\(L\text{,}\) entonces\(K\) disminuiremos y viceversa. \(\frac{dK}{dL}\)mide la pendiente de\(K\) ans una función de\(L\text{.}\)\(\frac{dL}{dK}\) mide la pendiente de\(L\) ans una función de\(K\text{.}\)

Ejercicio 14:

Dejar\(30*price+3*price*quantity+(quantity^2)/100=2000\) ser una ecuación que relaciona oferta y precio para artilugios. Encuentra\(\frac{d\ price}{d\ quantity}\) y\(\frac{d\ quantity}{d\ price}\text{.}\) explica lo que significa cada derivado.

Ejercicio 15:

\(e^{xy}+2x+3y=17\text{.}\)Encuentra\(\frac{dy}{dx}\text{.}\)

Responder

\[ \frac{d}{dx} (e^{xy}+2x+3y)= \frac{d}{dx} 17 \nonumber \]

Evaluando los derivados:

\[ e^{xy} \frac{d}{dx} (xy)+2+3 \frac{dy}{dx}=0 \nonumber \]

Lo que da:

\[ e^{xy} [y+x \frac{dy}{dx}]+2+3 \frac{dy}{dx}=0 \nonumber \]

A continuación resolvemos para\(\frac{dy}{dx}\)

\[ e^{xy} y+xe^{xy} \frac{dy}{dx}+2+3 \frac{dy}{dx}=0 \nonumber \]

\[ (xe^{xy}+3)\frac{dy}{dx}=-(e^{xy} y+2) \nonumber \]

\[ \frac{dy}{dx}=-\frac{(y e^{xy}+2)}{(x e^{xy}+3)} \nonumber \]