Saltar al contenido principal
LibreTexts Español

2.16: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110520

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    1. Para decidir sobre un nuevo diseño de sitio web, el diseñador pide a la gente clasificar tres diseños que han sido creados (etiquetados A, B y C). A continuación se muestran las boletas individuales. Crear una tabla de preferencias.

    ABC, ABC, ACB, BAC, BCA, BCA, ACB, CAB, CAB, BCA, ACB, ABC

    1. Para decidir sobre una película para ver, un grupo de amigos votan por una de las opciones (etiquetada A, B y C). A continuación se muestran las boletas individuales. Crear una tabla de preferencias.

    TAXI, CBA, BAC, BCA, CBA, ABC, ABC, CBA, BCA, CAB, CAB, BAC

    1. El comité de planeación de una feria de energías renovables está tratando de decidir en qué ciudad celebrar su próxima feria. A continuación se muestran los votos.

    \ (\ begin {array} {|c|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ textbf {9} &\ textbf {19} &\ textbf {11} &\ textbf {8}\\
    \ hline\ textbf {1st choice} &\ text {Buffalo} &\ text {Atlanta} &\ text {Chicago} &\ texto {Búfalo}\\
    \ hline\ textbf {2a opción} &\ text {Atlanta} &\ text {Buffalo} &\ text {Buffalo} &\ text {Chicago}\\\ hline
    \ textbf {3a opción} &\ text {Chicago} &\ text {Chicago} &\ text {Atlanta} &\ text {Atlanta} &\ text {Atlanta}\
    \ hline
    \ end {array}\)

    1. ¿Cuántos votantes votaron en esta elección?
    2. ¿Cuántos votos se necesitan para la mayoría? ¿Una pluralidad?
    3. Encuentra al ganador bajo el método de pluralidad.
    4. Encuentra al ganador bajo el Método de Recuento de Borda.
    5. Encuentra al ganador bajo el método Instant Runoff Votion.
    6. Encuentra al ganador bajo el método de Copeland.
    1. Una agencia sin fines de lucro está eligiendo un nuevo presidente de la junta. A continuación se muestran los votos.

    \ (\ begin {array} {|c|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ mathbf {1 1} &\ mathbf {5} &\ mathbf {1 0} &\ mathbf {3}\\ hline
    \ textbf {1st choice} &\ text {Atkins} &\ text {Cortez} &\ text {Cortez} &\ text {} &\ texto {Atkins}\\
    \ hline\ textbf {2nd choice} &\ text {Cortez} &\ text {Burke} &\ text {Cortez} &\ text {Burke}\\ hline
    \ textbf {3a opción} &\ text {Burke} &\ text {Atkins} &\ text {Atkins} &\ text {Atkins} &\ text {Cortez}\
    \ hline
    \ end {array}\)

    1. ¿Cuántos votantes votaron en esta elección?
    2. ¿Cuántos votos se necesitan para la mayoría? ¿Una pluralidad?
    3. Encuentra al ganador bajo el método de pluralidad.
    4. Encuentra al ganador bajo el Método de Recuento de Borda.
    5. Encuentra al ganador bajo el método Instant Runoff Votion.
    6. Encuentra al ganador bajo el método de Copeland.
    1. El gobierno estudiantil realiza elecciones para presidente. Hay cuatro candidatos (etiquetados A, B, C y D por conveniencia). El horario de preferencia para la elección es:

    \ (\ begin {array} {|c|c|c|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ mathbf {1 2 0} &\ mathbf {5 0} &\ mathbf {4 0} &\ mathbf {9 0} &\ mathbf {6 0} &\ mathbf {1 0 0}\
    \ hline\ tbtbf {1ª opción} &\ mathrm {C} &\ mathrm {B} &\ mathrm {D} &\ mathrm {A} &\ mathrm {A} &\ mathrm {D}\\ hline
    \ textbf {2a opción} &\ mathrm {D} &\ mathrm {C} &\ mathrm {A} &\ mathrm {C} &\ mathrm {D} &\ mathrm {B}\\ hline
    \ textbf {3a opción} &\ mathrm {B} &\ mathrm {B} &\ mathrm {A} &\ mathrm {B} &\ mathrm {B} &\ mathrm {C} & amp;\ mathrm {A}\\
    \ hline\ textbf {4ta opción} &\ mathrm {A} &\ mathrm {D} &\ mathrm {C} &\ mathrm {D} &\ mathrm {B} &\ mathrm {C}\
    \ hline
    \ end {array}\)

    1. ¿Cuántos votantes votaron en esta elección?
    2. ¿Cuántos votos se necesitan para la mayoría? ¿Una pluralidad?
    3. Encuentra al ganador bajo el método de pluralidad.
    4. Encuentra al ganador bajo el Método de Recuento de Borda.
    5. Encuentra al ganador bajo el método Instant Runoff Votion.
    6. Encuentra al ganador bajo el método de Copeland.
    1. La asociación de propietarios está decidiendo un nuevo conjunto de estándares vecinales para arquitectura, mantenimiento de patios, etc. Se han propuesto cuatro opciones. Los votos son:

    \ (\ begin {array} {|c|c|c|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ mathbf {8} &\ mathbf {9} &\ mathbf {1 1} &\ mathbf {7} &\ mathbf {7} &\ mathbf {5}\\ hline\ textbf {1a opción} &\ mathbf {5}\\ hline
    \ textbf {1a opción} &\ mathbf {5}\\ hline\ textbf texto {B} &\ texto {A} &\ texto {D} &\ texto {A} & \ texto {B} &\ texto {C}\\
    \ hline\ textbf {2ª opción} &\ texto {C} &\ texto {D} &\ texto {B} &\ texto {B} &\ texto {A} &\ texto {D}\
    \ hline\ textbf {3a opción} &\ texto {A} &\ texto {C} &\ texto {C} &\ texto {D} y\ texto {C} &\ texto {A}\\
    \ hline\ textbf {4ta opción} &\ texto {D} &\ texto {B} &\ texto {A} &\ texto {C} &\ texto {D} &\ texto {B}\
    \ hline
    \ final {matriz}\)

    1. ¿Cuántos votantes votaron en esta elección?
    2. ¿Cuántos votos se necesitan para la mayoría? ¿Una pluralidad?
    3. Encuentra al ganador bajo el método de pluralidad.
    4. Encuentra al ganador bajo el Método de Recuento de Borda.
    5. Encuentra al ganador bajo el método Instant Runoff Votion.
    6. Encuentra al ganador bajo el método de Copeland.
    1. Considera una elección con 129 votos.
      1. Si hay 4 candidatos, ¿cuál es el menor número de votos que podría tener un candidato de pluralidad?
      2. Si hay 8 candidatos, ¿cuál es el menor número de votos que podría tener un candidato de pluralidad?
    1. Considera una elección con 953 votos.
      1. Si hay 7 candidatos, ¿cuál es el menor número de votos que podría tener un candidato de pluralidad?
      2. Si hay 8 candidatos, ¿cuál es el menor número de votos que podría tener un candidato de pluralidad?
    1. ¿Este sistema de votación tiene un Candidato Condorcet? Si es así, encuéntralo.

    \ (\ begin {array} {|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ mathbf {1 4} &\ mathbf {1 5} &\ mathbf {2}\
    \ hline\ textbf {1a opción} &\ mathrm {A} &\ mathrm {C} &\ mathrm {B}\
    \\ hline\ tbf {2a opción} &\ mathrm {B} &\ mathrm {B} &\ mathrm {C}\\
    \ hline\ textbf {3a opción} &\ mathrm {C} &\ mathrm {A} &\ mathrm {A}\\
    \ hline
    \ end {array}\)

    1. ¿Este sistema de votación tiene un Candidato Condorcet? Si es así, encuéntralo.

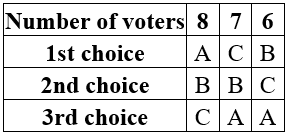
    clipboard_eecd05381cdae5dd73621622d8604dc6b.png

    1. El comité de mercadotecnia de una empresa decide votar sobre un nuevo logotipo de la compañía. Deciden utilizar el voto de aprobación. Sus resultados se cuentan a continuación. Cada columna muestra el número de electores con el voto de aprobación particular. ¿Qué logotipo gana bajo votación de aprobación?

    \ (\ begin {array} {|c|c|c|c|}
    \ hline\ textbf {Número de votantes} &\ mathbf {8} &\ mathbf {7} &\ mathbf {6}\
    \\ hline\ textbf {1a opción} &\ mathrm {A} &\ mathrm {C} &\ mathrm {B}
    \\ hline\ tbf {2ª opción} &\ mathrm {B} &\ mathrm {B} & ;\ mathrm {C}\\
    \ hline\ textbf {3a opción} &\ mathrm {C} &\ mathrm {A} &\ mathrm {A}\\
    \ hline
    \ end {array}\)

    1. La asociación empresarial del centro está eligiendo un nuevo presidente, y decide utilizar la votación de aprobación. El recuento se encuentra a continuación, donde cada columna muestra el número de electores con el voto de aprobación particular. ¿Qué candidato gana bajo votación de aprobación?

    \ (\ begin {array} {|c|c|c|c|c|c|c|c|c|}
    \ hline\ textbf {número de votantes} &\ mathbf {8} &\ mathbf {7} &\ mathbf {6} &\ mathbf {3} &\ mathbf {4} &\ mathbf {2} &\ mathbf {5}\
    \ hline\ mathbf bf {A} &\ mathrm {X} &\ mathrm {X} & & &\ mathrm {X} & & ;\ mathrm {X}\
    \ hline\ mathbf {B} &\ mathrm {X} &\ mathrm {X} &\ mathrm {X} & &\ mathrm {X} &\
    mathrm {X}\\ hline\ mathbf {C} &\ mathrm {X} &\ mathrm {X} &\ mathrm {X} &\ mathrm {X} &\
    \ hline\ mathbf {D} &\ mathrm {X} & ; &\ mathrm {X} &\ mathrm {X} &\ mathrm {X} &\\
    \ hline
    \ end {matriz}\)

    This page titled 2.16: Ejercicios is shared under a CC BY-SA 3.0 license and was authored, remixed, and/or curated by David Lippman (The OpenTextBookStore) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.