17.9: Evaluación de argumentos deductivos con diagramas de Euler

Última actualización
Guardar como PDF

Page ID: 110785

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

Podemos interpretar un argumento deductivo visualmente con un diagrama de Euler, que es esencialmente lo mismo que un diagrama de Venn. Esto puede facilitar la determinación de si el argumento es válido o no válido.

Ejemplo 31

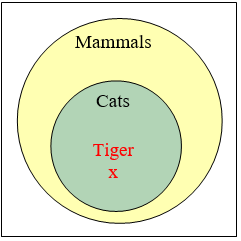
Considera el argumento deductivo “Todos los gatos son mamíferos y un tigre es un gato, por lo que un tigre es un mamífero”. ¿Es válido este argumento?

Solución

$Un gran círculo etiquetado Mamíferos. En el interior hay un círculo más pequeño etiquetado como Gatos. En su interior hay un tigre con la etiqueta X.$ Las premisas son:

Todos los gatos son mamíferos.

Un tigre es un gato.

La conclusión es:

Un tigre es un mamífero.

Ambas premisas son verdaderas. Para ver que las premisas deben llevar lógicamente a la conclusión, podemos usar un diagrama de Venn. Desde la primera premisa, dibujamos el conjunto de gatos como un subconjunto del conjunto de mamíferos. Desde la segunda premisa, se nos dice que un tigre está contenido dentro del conjunto de gatos. A partir de eso, podemos ver en el diagrama de Venn que el tigre también debe estar dentro del conjunto de mamíferos, por lo que la conclusión es válida.

Analizando argumentos con diagramas de Euler

Para analizar un argumento con un diagrama de Euler:

1) Dibujar un diagrama de Euler basado en las premisas del argumento

2) El argumento no es válido si hay una manera de dibujar el diagrama que haga falsa la conclusión

3) El argumento es válido si no se puede dibujar el diagrama para hacer falsa la conclusión

4) Si las premisas son insuficientes para determinar la ubicación de un elemento o un conjunto mencionado en la conclusión, entonces el argumento no es válido.

Pruébalo ahora 9

Determinar la validez de este argumento:

$\begin{array} {ll} \text{Premise:} & \text{All cats are scared of vacuum cleaners.} \\ \text{Premise:} & \text{Max is a cat.} \\ \text{Conclusion:} & \text{Max is scared of vacuum cleaners.} \end{array}$

Contestar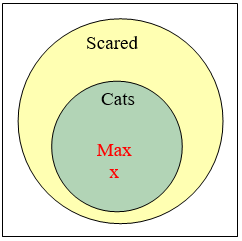: $Un círculo grande etiquetado Asustado, con un círculo dentro etiquetado Cats. Una mancha etiquetada como Max está dentro del círculo de gatos.$ Válido. Los gatos son un subconjunto de criaturas que están asustadas por las aspiradoras. Max está en el set de gatos, por lo que también debe estar en el conjunto de criaturas que están asustadas por las aspiradoras.

Ejemplo 32

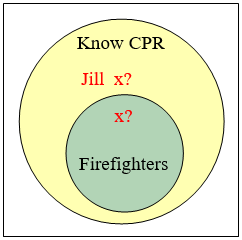$Un círculo grande con la etiqueta Saber RCP. En el interior hay un círculo más pequeño etiquetado como Bomberos. Hay dos lugares marcados a Jill con un signo de interrogación: uno dentro del círculo de bomberos y otro afuera.$ $\begin{array} {ll} \text{Premise:} & \text{All firefighters know CPR.} \\ \text{Premise:} & \text{Jill knows CPR.} \\ \text{Conclusion:} & \text{Jill is a firefighter.} \end{array}$

Solución

Desde la primera premisa, sabemos que todos los bomberos se encuentran dentro del conjunto de quienes conocen la RCP. (Los bomberos son un subconjunto de personas que conocen RCP.) Desde la segunda premisa, sabemos que Jill es miembro de ese conjunto más grande, pero no tenemos suficiente información para saber si ella también es miembro del subconjunto más pequeño que son los bomberos.

Dado que la conclusión no necesariamente se desprende de las premisas, se trata de un argumento inválido. Es posible que Jill sea bombero, pero la estructura del argumento no nos permite concluir que definitivamente lo es.

Es importante señalar que si Jill es o no realmente bombero no es importante para evaluar la validez del argumento; nos preocupa si las premisas son suficientes para probar la conclusión.

Pruébalo ahora 10

Determinar la validez de este argumento:

$\begin{array} {ll} \text{Premise:} & \text{All bicycles have two wheels.} \\ \text{Premise:} & \text{This Harley-Davidson has two wheels.} \\ \text{Conclusion:} & \text{This Harley-Davidson is a bicycle.} \end{array}$

Contestar: $Un círculo grande etiquetado dos ruedas, y un círculo dentro etiquetado Bicicletas. Hay dos spots etiquetados como Harley con signo de interrogación, uno dentro del círculo de bicicletas, y el otro dentro del círculo de dos ruedas pero fuera del círculo de la bicicleta.$ No válido. El conjunto de bicicletas es un subconjunto del conjunto de vehículos con dos ruedas; la Harley-Davidson está en el conjunto de vehículos de dos ruedas pero no necesariamente en el círculo más pequeño.

Pruébalo ahora 11

Determinar la validez de este argumento:

$\begin{array} {ll} \text{Premise:} & \text{No cows are purple.} \\ \text{Premise:} & \text{Fido is not a cow.} \\ \text{Conclusion:} & \text{Fido is purple.} \end{array}$

Contestar: $Dos círculos que no se superponen, uno etiquetado como Vacas y el otro etiquetado Cosas Moradas. Hay dos manchas marcadas con Fido con un signo de interrogación, una dentro del círculo de las cosas moradas, y la otra dentro de ninguno de los dos círculos.$ No válido. Como ninguna vaca es morada, sabemos que no hay superposición entre el conjunto de vacas y el conjunto de cosas moradas. Sabemos que Fido no está en el set de vacas, pero eso no es suficiente para concluir que Fido está en el conjunto de las cosas moradas.

Además de estas premisas de estilo categórico de la forma “todos ___”, “algunos ____”, y “no ____”, también es común ver premisas que son condicionales.

Ejemplo 33

$\begin{array} {ll} \text{Premise:} & \text{If you live in Seattle, you live in Washington.} \\ \text{Premise:} & \text{Marcus does not live in Seattle.} \\ \text{Conclusion:} & \text{Marcus does not live in Washington.} \end{array}$

Solución

Desde la primera premisa, sabemos que el conjunto de personas que viven en Seattle está dentro del conjunto de quienes viven en Washington. Desde la segunda premisa, sabemos que Marcus no miente en el set de Seattle, pero no tenemos suficiente información para saber si Marcus vive en Washington o no. Este es un argumento inválido.

$Un círculo grande etiquetado como Washington, con un círculo más pequeño etiquetado Seattle en su interior. Hay dos spots etiquetados Marcus con un signo de interrogación: uno dentro del círculo de Washington pero fuera del Seattle uno, y el otro fuera del círculo de Washington.$

Tryt it Now 12

Determinar la validez de este argumento:

$\begin{array} {ll} \text{Premise:} & \text{If you have lipstick on your collar, then you are cheating on me.} \\ \text{Premise:} & \text{If you are cheating on me, then I will divorce you.} \\ \text{Premise:} & \text{ You do not have lipstick on your collar.} \\ \text{Conclusion:} & \text{I will not divorce you.} \end{array}$

Contestar: $Un círculo etiquetado Divorcio, con un círculo dentro etiquetado Cheating, con un círculo dentro que etiquetaba Lipstick. Hay tres puntos etiquetados Tú con un signo de interrogación: uno fuera de todos los círculos, uno dentro del círculo de Divorcio pero fuera del círculo de Hacer trampa, y el último dentro del círculo de Hacer trampa pero fuera del círculo de Lipstick.$ No válido. El lápiz labial en tu cuello es un subconjunto de escenarios en los que estás engañando, y el engaño es un subconjunto de los escenarios en los que me divorciaré de ti. A pesar de que es maravilloso que no tengas pintalabios en el cuello, aún podrías estar engañándome, y yo me divorciaré de ti. De hecho, aunque no me estés engañando, podría divorciarme de ti por otra razón. Será mejor que te pongas en forma.