1.1: Graficando una Ecuación Lineal
- Page ID
- 113589
En esta sección, aprenderás a:
- Grafica una línea cuando conoces su ecuación
- Graficar una línea cuando se le da su ecuación en forma paramétrica
- Graficar y encontrar ecuaciones de líneas verticales y horizontales
Graficando una Línea a partir de ella Ecuación
Las ecuaciones cuyas gráficas son líneas rectas se denominan ecuaciones lineales. Los siguientes son algunos ejemplos de ecuaciones lineales:
\(2 x-3 y=6, \quad 3 x=4 y-7, \quad y=2 x-5, \quad 2 y=3, \quad \text { and } \quad x-2=0\)
Una línea está completamente determinada por dos puntos. Por lo tanto, para graficar una ecuación lineal necesitamos encontrar las coordenadas de dos puntos. Esto se puede lograr eligiendo un valor arbitrario para x o y luego resolviendo para la otra variable.
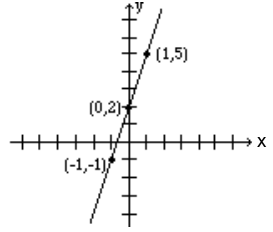
Grafica la línea:\(y = 3x + 2\)
Solución
Necesitamos encontrar las coordenadas de al menos dos puntos. Elegimos arbitrariamente x = - 1, x = 0 y x = 1.
- Si x = -1, entonces y = 3 (-1) + 2 o -1. Por lo tanto, (-1, -1) es un punto en esta línea.
- Si x = 0, entonces y = 3 (0) + 2 o y = 2. De ahí el punto (0, 2).
- Si x = 1, entonces y = 5, y obtenemos el punto (1, 5).
A continuación, se resumen los resultados y se grafica la línea.
| x | -1 | 0 | 1 |
| y | -1 | 2 | 5 |
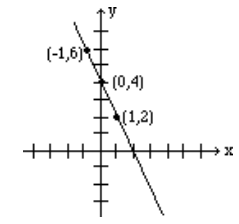
Grafica la línea:\(2x + y = 4\)
Solución
Nuevamente, necesitamos encontrar coordenadas de al menos dos puntos.
Elegimos arbitrariamente x = -1, x = 0 e y = 2.
- Si x = -1, entonces 2 (-1) + y = 4 lo que resulta en y = 6. Por lo tanto, (-1, 6) es un punto en esta línea.
- Si x = 0, entonces 2 (0) + y = 4, lo que resulta en y = 4. De ahí el punto (0, 4).
- Si y = 2, entonces 2x + 2 = 4, lo que rinde x = 1, y da el punto (1, 2).
En la siguiente tabla se muestran los puntos, y se grafica la línea.
| x | -1 | 0 | 1 |
| y | 6 | 4 | 2 |
Intercepta
Los puntos en los que una línea cruza los ejes de coordenadas se denominan intercepciones.
Al graficar una línea trazando dos puntos, a menudo se prefiere usar las intercepciones porque son fáciles de encontrar.
- Para encontrar el valor de la intercepción x, dejamos que y = 0
- Para encontrar el valor de la intercepción y, dejamos x = 0.
Encuentra las intercepciones de la línea:\(2x - 3y = 6\), y grafica.
Solución
Para encontrar la intercepción x, deje y = 0 en la ecuación, y resuelva para x.
\[\begin{align*} 2x - 3(0) &= 6 \\[4pt] 2x - 0 &= 6 \\[4pt] 2x &= 6 \\[4pt] x &= 3 \end{align*} \nonumber \]
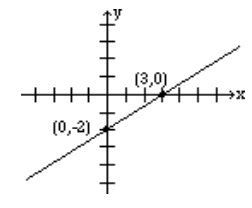
Por lo tanto, la intercepción x es el punto (3,0).
Para encontrar la intercepción y, deje x = 0 en la ecuación, y resuelva para y.
\[\begin{align*} 2(0) - 3y &= 6 \\[4pt] 0 - 3y &= 6 \\[4pt] -3y &= 6 \\[4pt] y &= -2 \end{align*} \nonumber \]
Por lo tanto, la intercepción y es el punto (0, -2).
Para graficar la línea, grafica los puntos para la intercepción x (3,0) y la intercepción y (0, -2), y utilízalos para dibujar la línea.
Graficando una Línea a partir de su Ecuación en Forma Paramétrica
En matemáticas superiores, las ecuaciones de líneas a veces se escriben en forma paramétrica. Por ejemplo,\(x = 3 + 2t\),\(y = 1 + t\). La letra\(t\) se llama el parámetro, o la variable ficticia.
Las líneas paramétricas se pueden graficar encontrando valores para x e y sustituyendo valores numéricos por t. Trazar los puntos usando sus coordenadas (x, y) y use los puntos para dibujar la línea.
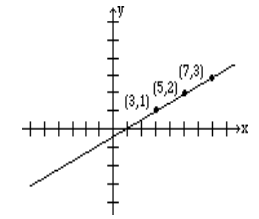
Grafica la línea dada por las ecuaciones paramétricas:\(x = 3 + 2t\),\(y = 1 + t\)
Solución
Sea t = 0, 1 y 2; para cada valor de t encuentre los valores correspondientes para x e y.
Los resultados se dan en la siguiente tabla.
| t | x | y | Punto en Línea |
|---|---|---|---|
| 0 | 3 | 1 | (3, 1) |
| 1 | 5 | 2 | (5, 2) |
| 2 | 7 | 3 | (7, 3) |
Líneas Horizontales y Verticales
Cuando una ecuación de una línea tiene solo una variable, la gráfica resultante es una línea horizontal o vertical.
- El gráfico de la línea\(x = a\), donde\(a\) es una constante, es una línea vertical que pasa por el punto\((a, 0)\). Cada punto de esta línea tiene la coordenada x igual a a, independientemente de la coordenada y.
- El gráfico de la línea\(y = b\), donde\(b\) es una constante, es una línea horizontal que pasa por el punto\((0, b)\). Cada punto de esta línea tiene la coordenada y igual a b, independientemente de la coordenada x.
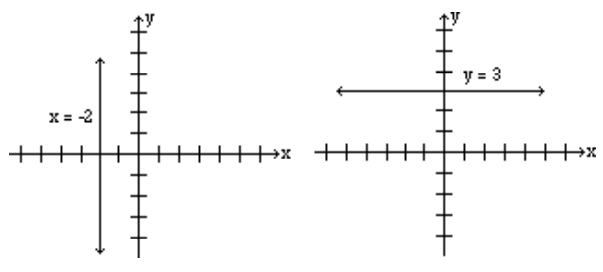
Grafica las líneas: x = -2, e y = 3.
Solución
El gráfico de la línea x = -2 es una línea vertical que tiene la coordenada x -2 sin importar cuál sea la coordenada y. La gráfica es una línea vertical que pasa por el punto (-2, 0).
El gráfico de la línea y = 3, es una línea horizontal que tiene la coordenada y 3 independientemente de cuál sea la coordenada x. Por lo tanto, la gráfica es una línea horizontal que pasa por el punto (0, 3).
Nota: La mayoría de los estudiantes sienten que las coordenadas de los puntos deben ser siempre enteros. Esto no es cierto, y en situaciones de la vida real, no siempre es posible. No se deje intimidar si sus puntos incluyen números que son fracciones o decimales.


