1.2: Pendiente de una Línea

Última actualización
Guardar como PDF

Page ID: 113596

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

En esta sección, aprenderás a:

Encuentra la pendiente de una línea.
Grafica la línea si se da un punto y la pendiente.

En la última sección, aprendimos a graficar una línea eligiendo dos puntos en la línea. También se puede determinar una gráfica de una línea si se conoce un punto y la “pendiente” de la línea. El número que se refiere a la inclinación o inclinación de una línea se denomina pendiente de la línea.

De cursos previos de matemáticas, muchos de ustedes recuerdan la pendiente como el “ascenso sobre carrera” o “el cambio vertical sobre el cambio horizontal” y a menudo la han visto expresada como:

\[\frac{\text {rise}}{\text {run}}, \frac{\text {vertical change}}{\text {horizontal change}}, \frac{\Delta y}{\Delta x} \text { etc. } \nonumber \]

Damos una definición precisa.

Definición: Pendiente

Si ($x_1$,$y_1$) y ($x_2$,$y_2$) son dos puntos diferentes en una línea, la pendiente de la línea es

\[\text{slope}=m=\frac{y_2-y_1}{x_2-x_1} \label{slope} \]

Ejemplo$\PageIndex{1}$

Encuentra la pendiente de la línea que pasa por los puntos (−2, 3) y (4, −1), y grafica la línea.

Solución

Let ($x_1$,$y_1$) = (−2, 3) y ($x_2$,$y_2$) = (4, −1), entonces la pendiente (vía Ecuación\ ref {pendiente}) es

$m = \frac{-1-3}{4-(-2)} = \frac{-4}{6} = -\frac{2}{3}$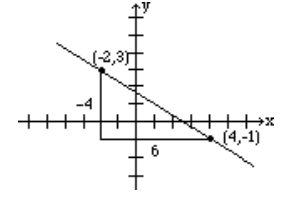

$Ejemplo1.2.1.png$

Para darle al lector una mejor comprensión, se muestran tanto el cambio vertical, -4, como el cambio horizontal, 6, en la figura anterior.

Cuando se dan dos puntos, no importa qué punto se denota como ($x_1$,$y_1$) y cuál ($x_2$,$y_2$). El valor para la pendiente será el mismo.

En Ejemplo$\PageIndex{1}$, si en su lugar elegimos ($x_1$,$y_1$) = (4, −1) y ($x_2$,$y_2$) = (−2, 3), entonces obtendremos el mismo valor para la pendiente que obtuvimos anteriormente.

Los pasos involucrados son los siguientes.

\[m = \frac{3-(-1)}{-2-4} = \frac{4}{-6} = -\frac{2}{3} \nonumber \]

El alumno deberá observar además que

si una línea sube al ir de izquierda a derecha, entonces tiene una pendiente positiva. En esta situación, a medida que$x$ aumenta el valor de,$y$ también aumenta el valor de
si una línea cae yendo de izquierda a derecha, tiene una pendiente negativa; a medida que$x$ aumenta el valor de, el valor de$y$ disminuye.

Ejemplo$\PageIndex{2}$

Encuentra la pendiente de la línea que pasa por los puntos (2, 3) y (2, −1), y grafica.

Solución

Let ($x_1$,$y_1$) = (2, 3) y ($x_2$,$y_2$) = (2, −1) entonces la pendiente es

\[m = \frac{-1-3}{2-2}=\frac{4}{0}=\text{undefined.} \nonumber \]

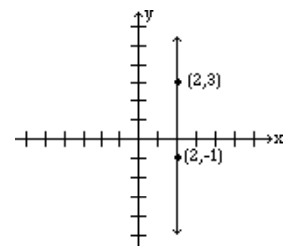
$Ejemplo1.2.2.png$

Nota: La pendiente de una línea vertical es indefinida.

Ejemplo$\PageIndex{3}$

Encuentra la pendiente de la línea que pasa por los puntos (−1, −4) y (3, −4)

Solución

Let ($x_1$,$y_1$) = (−1, −4) y ($x_2$,$y_2$) = (3, −4), entonces la pendiente es

\[ m = \frac{-4-(-4)}{3-(-1)} = \frac{0}{4} = 0 \nonumber \]

Nota: La pendiente de una línea horizontal es 0

Ejemplo$\PageIndex{4}$

Grafica la línea que pasa por el punto (1, 2) y tiene pendiente$-\frac{3}{4}$.

Solución

Pendiente es igual$\frac{\text{rise}}{\text{run}}$. El hecho de que la pendiente sea$\frac{-3}{4}$, significa que por cada subida de -3 unidades (caída de 3 unidades) hay una carrera de 4. Entonces si desde el punto dado (1, 2) bajamos 3 unidades y vamos a la derecha 4 unidades, llegamos al punto (5, -1). La gráfica se obtiene conectando estos dos puntos.

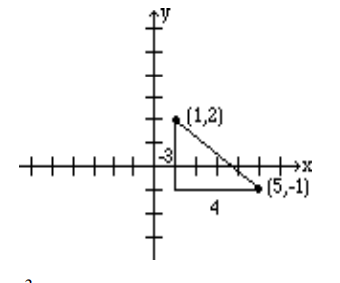
$Ejemplo1.2.4a.png$

Alternativamente, dado que$\frac{3}{-4}$ representa el mismo número, la línea se puede dibujar comenzando en el punto (1,2) y eligiendo una subida de 3 unidades seguida de una tirada de -4 unidades. Entonces desde el punto (1, 2), subimos 3 unidades, y hacia la izquierda 4, llegando así al punto (-3, 5) que también está en la misma línea. Ver la figura a continuación.

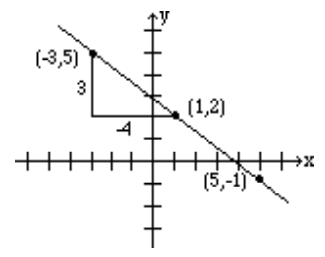
$Ejemplo1.2.4b.png$

Ejemplo$\PageIndex{5}$

Encuentra la pendiente de la línea$2x + 3y = 6$.

Solución

Para encontrar la pendiente de esta línea, elegiremos dos puntos cualesquiera en esta línea.

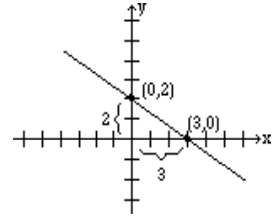
Nuevamente, la selección$x$ e$y$ intercepta parece ser una buena opción. El$x$ -intercepto es (3, 0), y el$y$ -intercepto es (0, 2). Por lo tanto, la pendiente es

\[m = \frac{2-0}{0-3} =-\frac{2}{3}. \nonumber \]

La gráfica de abajo muestra la línea y las$x$ -intercepta e$y$ -intercepta:

$Ejemplo1.2.5.png$

Ejemplo$\PageIndex{6}$

Encuentra la pendiente de la línea$y = 3x + 2$.

Solución

Nuevamente encontramos dos puntos en la línea, por ejemplo, (0, 2) y (1, 5). Por lo tanto, la pendiente es

\[m =\frac{5-2}{1-0} = \frac{3}{1} = 3. \nonumber \]

Mira las pendientes y las$y$ -intercepciones de las siguientes líneas.

La línea	pendiente	$y$-interceptar
$y=3x+2$	3	\ (y\) -intercepta">2
$y=-2x+5$	-2	\ (y\) -intercepta">5
$y=\frac{3}{2}x-4$	$\frac{3}{2}$	\ (y\) -intercepta">-4

No es casualidad que cuando se resuelve una ecuación de la línea para$y$, el coeficiente del$x$ término representa la pendiente, y el término constante representa la$y$ -intercepción.

En otras palabras, para la línea$y = mx + b$,$m$ es la pendiente, y$b$ es la$y$ -intercepción.

Ejemplo$\PageIndex{7}$

Determinar la pendiente y$y$ -intercepción de la línea$2x + 3y = 6$.

Solución

Resolvemos para$y$:

\ begin {alinear*}
&2 x+3 y=6\ nonumber\\
&3 y=-2 x+6\ nonumber\\
&y =( -2/3) x+2\ nonumber
\ end {align*}

La pendiente = el coeficiente del$x$ término = − 2/3.

El$y$ -intercept = el término constante = 2.

La línea	pendiente	\(y\)-interceptar
\(y=3x+2\)	3	\ (y\) -intercepta">2
\(y=-2x+5\)	-2	\ (y\) -intercepta">5
\(y=\frac{3}{2}x-4\)	\(\frac{3}{2}\)	\ (y\) -intercepta">-4

Objetivos de aprendizaje

Definición: Pendiente

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Ejemplo\(\PageIndex{5}\)

Ejemplo\(\PageIndex{6}\)

Ejemplo\(\PageIndex{7}\)