2.3: Sistemas de Ecuaciones Lineales — Casos Especiales
- Page ID
- 113855
En esta sección, aprenderás a:
- Determinar los sistemas lineales que no tienen solución.
- Resuelve los sistemas lineales que tienen infinitamente muchas soluciones.
Si consideramos la intersección de dos líneas en un plano, pueden suceder tres cosas.
- Las líneas se cruzan exactamente en un punto. A esto se le llama un sistema independiente.
- Las líneas son paralelas, por lo que no se cruzan. A esto se le llama un sistema inconsistente.
- Las líneas coinciden; se cruzan en infinitamente muchos puntos. Este es un sistema dependiente.
Las cifras que aparecen a continuación muestran los tres casos.
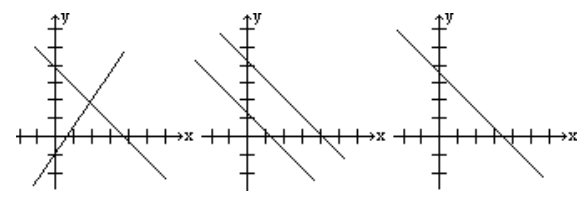
Cada sistema de ecuaciones tiene una solución, ninguna solución, o infinitamente muchas soluciones.
En la última sección, utilizamos el método Gauss-Jordan para resolver sistemas que tenían exactamente una solución. En esta sección, determinaremos los sistemas que no tienen solución, y resolveremos los sistemas que tienen infinitamente muchas soluciones.
Resuelve el siguiente sistema de ecuaciones:
\ begin {alineado}
x+y&=7\\
x+y&=9
\ end {alineado}
Solución
Usemos el método Gauss-Jordan para resolver este sistema. La matriz aumentada es
\ [\ left [\ begin {array} {llll}
1 & 1 & | & 7\\
1 & 1 & | & 9
\ end {array}\ right]\ quad\ left [\ begin {array} {l}
x+y=7\\
x+y=9
\ end {array}\ right]\ nonumber\]
Si multiplicamos la primera fila por - 1 y sumamos a la segunda fila, obtenemos
\ [\ left [\ begin {array} {llll}
1 & 1 & | & 7\\
0 & 0 & | & 2
\ end {array}\ right]\ quad\ left [\ begin {array} {l}
x+y=7\\
0 x+0 y=2
\ end {array}\ right]\ nonumber\]
Como 0 no puede ser igual a 2, la última ecuación no puede ser cierta para ninguna opción de x e y.
Alternativamente, es claro que las dos líneas son paralelas; por lo tanto, no se cruzan.
En los ejemplos que siguen, vamos a empezar a usar una calculadora para remar reducir la matriz aumentada, con el fin de enfocarnos en comprender la respuesta en lugar de enfocarnos en el proceso de llevar a cabo las operaciones de fila.
Resuelve el siguiente sistema de ecuaciones.
\ [\ begin {array} {l}
2 x+3 y-4 z=7\\
3 x+4 y-2 z=9\\
5 x+7 y-6 z=20
\ end {array}\ nonumber\]
Solución
Ingresamos la siguiente matriz aumentada en la calculadora.
\ [\ left [\ begin {array} {ccccc}
2 & 3 & -4 & | & 7\\
3 & 4 & -2 & | & 9\\
5 & 7 & -6 & | & 20
\ end {array}\ derecha]\ nonumber\]
Ahora al presionar la tecla para obtener la forma de fila-escalón reducida, obtenemos
\ [\ left [\ begin {array} {ccccc}
1 & 0 & 10 & | & 0\\
0 & 1 & -8 & | & 0\\
0 & 0 & 0 & | & 1
\ end {array}\ derecha]\ nonumber\]
En la última fila se afirma eso\(0x + 0y + 0z = 1\). Pero el lado izquierdo de la ecuación es igual
a 0. Entonces esta última fila dice 0 = 1, que es una contradicción, una declaración falsa.
Esta fila inferior indica que el sistema es inconsistente; por lo tanto, no hay solución.
Resuelve el siguiente sistema de ecuaciones.
\ begin {alineado}
x+y&=7\\
x+y&=7
\ end {alineado}
Solución
El problema claramente pide la intersección de dos líneas que son iguales; es decir, las líneas coinciden. Esto significa que las líneas se cruzan en un número infinito de puntos.
Algunos puntos de intersección se enumeran de la siguiente manera: (3, 4), (5, 2), (-1, 8), (-6, 13) etc. Sin embargo, cuando un sistema tiene un número infinito de soluciones, la solución a menudo se expresa en forma paramétrica. Esto se puede lograr asignando una constante arbitraria, t, a una de las variables, y luego resolviendo para las variables restantes. Por lo tanto, si lo dejamos\(y = t\), entonces\(x = 7 - t\). O podemos decir que todos los pares ordenados de la forma\((7 - t, t)\) satisfacen el sistema de ecuaciones dado.
Alternativamente, mientras resolvemos el método Gauss-Jordan, obtendremos la forma de fila-escalón reducida que se da a continuación.
\ [\ left [\ begin {array} {llll}
1 & 1 & | & 7\\
0 & 0 & | & 0
\ end {array}\ right]\ nonumber\]
La fila de todos los ceros, simplemente puede ser ignorada. Esta fila dice\(0x + 0y = 0\); no proporciona más información sobre los valores de x e y que resuelven este sistema.
Esto nos deja con una sola ecuación pero dos variables. Y siempre que haya más variables que las ecuaciones, la solución debe expresarse como una solución paramétrica en términos de una constante arbitraria, como antes.
Solución Paramétrica:\(\mathbf{x = 7 - t, y = t}\).
Resuelve el siguiente sistema de ecuaciones.
\ begin {alineado}
x+y+z&=2\\
2 x+y-z&=3\\
3 x+2 y&=5
\ end {alineado}
Solución
La matriz aumentada y la forma reducida fila-escalón se dan a continuación.
\ [\ left [\ begin {array} {ccccc}
1 & 1 & | & 2\\
2 & 1 & 1 & -1 & | & 3\\
3 & 2 & 0 & | & 5
\ end {array}\ derecha]\ text {Matriz aumentada para este sistema}\ nonumber\]
\ [\ left [\ begin {array} {ccccc}
1 & 0 & -2 & | & 1\\
0 & 1 & 3 & | & 1\\
0 & 0 & 0 & 0 & | & 0
\ end {array}\ derecha]\ text {Forma de escalón de fila reducida}\ nonumber\]
Desde que la última ecuación abandonó, nos quedamos con dos ecuaciones y tres variables. Esto significa que el sistema tiene un número infinito de soluciones. Expresamos esas soluciones en forma paramétrica dejando que la última variable\(z\) sea igual al parámetro\(t\).
La primera ecuación dice\(x - 2z = 1\), por lo tanto,\(x = 1 + 2z\).
La segunda ecuación dice\(y + 3z = 1\), por lo tanto,\(y = 1 - 3z\).
Y ahora si lo dejamos\(z = t\), la solución paramétrica se expresa de la siguiente manera:
Solución Paramétrica:\(\mathbf{x=1+2t, \quad y=1-3t, \quad z=t}\).
El lector debe tener en cuenta que se pueden obtener soluciones particulares, o soluciones específicas, al sistema asignando valores al parámetro t. Por ejemplo:
- si lo dejamos\(t = 2\), tenemos la solución\(x = 5, y = -5, z = 2\):\((5, -5, 2)\)
- si lo dejamos\(t = 0\), tenemos la solución\(x = 1, y = 1, z = 0\):\((1, 1, 0)\).
Resuelve el siguiente sistema de ecuaciones.
\[\begin{align*} x + 2y - 3z &= 5 \\[4pt] 2x + 4y - 6z &= 10 \\[4pt] 3x + 6y - 9z &= 15 \end{align*} \nonumber \]
Solución
La forma reducida de fila-escalón se da a continuación.
\ [\ left [\ begin {array} {ccccc}
1 & 2 & -3 & | & 5\\
0 & 0 & 0 & | & 0\\ 0 & 0 &
0 & | & 0 & 0 & | & 0
\ end {array}\ derecha]\ nonumber\]
Esta vez abandonan las dos últimas ecuaciones. Nos quedamos con una ecuación y tres variables. Nuevamente, hay un número infinito de soluciones. Pero esta vez la respuesta debe expresarse en términos de dos constantes arbitrarias.
Si dejamos\(z = t\) y dejamos\(y = s\), la primera ecuación\(x + 2y -3z = 5\) resulta en\(x = 5 - 2s + 3t\).
Reescribimos la solución paramétrica:\(\mathbf{x = 5 - 2s + 3t, \quad y = s, \quad z = t}\).
Resumimos nuestra discusión en la siguiente tabla.
- Si alguna fila de la forma fila-escalón reducida de la matriz da una declaración falsa como 0 = 1, el sistema es inconsistente y no tiene solución.
- Si la forma de escalón de fila reducida tiene menos ecuaciones que las variables y el sistema es consistente, entonces el sistema tiene un número infinito de soluciones. Recuerda que se dejan caer las filas que contienen todos los ceros.
- Si un sistema tiene un número infinito de soluciones, la solución debe expresarse en forma paramétrica.
- El número de parámetros arbitrarios es igual al número de variables menos el número de ecuaciones.


